IEEE 802.11 DCF機制下的異構網絡業務分析模型*

張朝柱,黃文鈺,尹冬梅

(哈爾濱工程大學 信息與通信工程學院,黑龍江 哈爾濱 150001)

IEEE 802.11[1,2]系列標準協議作為無線局域網、無線自組網等領域應用最廣泛的無線網絡協議,能夠快速通過相對簡單的本地網絡配置,實現包括不限于家庭、辦公場所以及公共場所的無線網絡的接入與共享.其中,DCF(distributed coordination function)機制得益于其全面的分布式設計以及實現的簡便性與資源共享的公平性,使之成為IEEE 802.11協議最基本的信道接入方式.因此,對DCF機制進行合理的、準確的建模,成為當前計算機與通信領域的熱點話題之一[3-22].

2000年Bianchi[4]首次提出利用二維穩態Markov鏈路模型對IEEE 802.11 DCF機制進行建模,通過對該穩態模型的求解,可以求出任意時隙的發送概率和失敗概率,從而導出飽和模型的性能,并由此引發對DCF機制建模大量的深入研究.但作者假設的信道是無錯的理想信道,模型中節點總處于飽和工作狀態,即任意時刻都存在數據包等待發送,重傳次數無限制,以及退避過程是連續的.而這一系列假設往往是不存在的.為了解決這一系列問題,眾多學者基于文獻[4]對DCF機制進行了深入的研究,提出了各種改進的算法模型來研究協議的吞吐量和傳輸時延,同時利用新的模型討論與優化協議的相關部分.Mao等人[5]提出了一種比較全面的飽和Markov模型,考慮了重傳限制以及退避凍結.Yang等人[6]提出一種改進的非飽和 Markov模型,但未考慮退避凍結引起的時隙變化等問題.Kosek-Szott等人[7]提出用非飽和Markov模型研究不同的AC(access category)接入類別的增強型分布協調功能EDCA(enhanced distributed channel access)的性能,但在時隙凍結及不飽和概率等問題上考慮不足.文獻[8,9]則分別聚焦于采用反向傳輸機制和采用不同服務優先級下的幀聚合的性能,由于模型相對簡化,因此建模不太準確.文獻[10,11]進一步完善了非飽和馬爾可夫模型,分析了分段分塊(packet fragmentation)機制及反向傳輸機制的DCF機制的性能,但對于傳輸完成后有無數據包存在于緩存中的概率考慮不夠完善.Zhao等人主要討論了M/G/1[12]排隊模型在非飽和場景下的應用,首次詳細討論了緩存大小對DCF性能的影響,同時得出與M/M/1/K模型相比,M/G/1模型能夠更準確地分析非飽和工作站點的性能.文獻[13,14]利用簡單的Markov模型對 EDCA進行了相關的分析與討論.文獻[15,16]則聚焦于對 DCF退避機制進行適當的調整優化,并利用 Markov模型對改進的機制進行建模分析.Chen等人[17]提出了利用信號估計與檢測中的理論,利用后驗概率進行均值計算求出站點的不飽和概率,同時與通過不完善的非飽和Markov模型求得的不飽和概率進行了均方誤差意義下的對比.

在現實場景中,異構網絡是最廣泛存在的,如不同的業務成分同時接入無線網絡其不飽和性是不同的,因此,對異構網絡的建模是至關重要的.據我們所知,只有文獻[18,19]對異構混合業務成分下的DCF機制進行了建模,其中,Nguyen等人[18]采用均值分析的方法對 DCF機制的性能進行分析評估,但簡單的均值分析并不能較好地模擬退避過程中的時隙凍結等問題,因而雖然算法相對簡單卻并不太準確.Kosek-Szott[19]則利用了 Markov模型對 DCF機制進行了較文獻[18]更為準確、合理的建模,但在算法上仍存在不少的不足之處,包括但不限于未考慮傳輸誤碼率、未全面考慮最大重傳次數的限制、傳輸概率考慮不夠周到以及不飽和性的分析方法復雜且不夠準確.為了進一步更為準確、完善地研究IEEE 802.11協議的相關內容,同時為參與IEEE 802.11協議的設計與分析的人員提供一定的參考價值.討論、分析了協議[1,2]的相關內容,提出了一種較文獻[19]更全面的基于Markov模型的異構混合業務下IEEE 802.11 DCF機制的性能分析模型.在模型中,充分考慮到了應用場景中飽和業務與非飽和業務混雜的實際情況,重點考慮了站點的退避凍結和有限重傳次數限制問題,同時結合M/G/1排隊模型[11],通過對提出的Markov模型進行穩態求解,導出了IEEE 802.11 DCF機制的吞吐量、傳輸時延及丟包率,同時分析、討論了緩存對系統性能的影響.

本文第1節對IEEE 802.11 DCF機制進行較為詳細的介紹及說明.第2節利用Markov對DCF機制進行合理建模.第3節針對提出的模型給出具體的計算方法與定義.第4節對提出的算法進行仿真分析,同時與近年來國內外相關的優秀算法進行比較.第5節對進行的研究工作及接下來的工作目標進行簡要的總結.

1 IEEE 802.11 DCF解析

DCF是一種被 IEEE 802.11標準所采用的分布式介質接入機制,采用了基于載波偵聽多路訪問/沖突避免(carrier sense multiple access with collision avoidance,簡稱CSMA/CA)的接入模式.工作原理是:數據傳輸發起站點通過能量檢測(ED)、載波檢測(CS)和能量載波混合檢測等方式來檢測信道的狀態,從而進行沖突規避[3].

為了減少數據通信過程中由于碰撞導致的傳輸失敗的幾率,DCF機制將 CSMA/CA接入模式與隨機退避過程相結合.當站點有數據需要進行傳輸時,站點需要進行隨機退避.在退避過程中每當偵聽到信道空閑且空閑時隙滿足一個IEEE 802.11協議定義的最小時隙長度slottime時,需要將退避計數器的數值減1；而每次偵聽到信道繁忙,需要凍結退避計數器計數狀態,若是偵聽到一次成功傳輸時需等待一個分布式協調功能幀間間隔DIFS(DCF inter-frame space)時長或偵聽到一次失敗傳輸時則需等待一個擴展幀間間隔 EIFS(extended interframe space)時長,才可以重新進行退避計數.如此反復進行,直到計數器值減至0,才可以發起數據的傳輸.而每次傳輸失敗后,需進行二進制退避,直至將退避窗口設置為最大；每次傳輸成功或重傳次數達到系統所設置的最大值,需要將退避窗口大小設置為最小.直到站點有新的數據包需要傳輸時,站點需要重新從最小退避窗口中隨機選擇退避時隙進行隨機退避過程[3].同時,退避時間可表示為

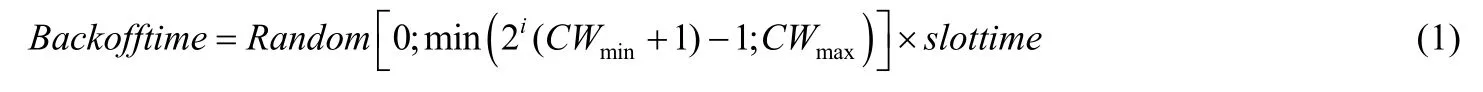
其中,i表示重傳次數,CWmin為最小退避窗口值,CWmax為最大退避窗口值.

根據對DCF機制退避過程的有效分析及合理討論,可以得出Markov鏈路模型能夠充分描述契合DCF機制的退避過程,因此可以利用Markov模型對DCF機制進行準確、合理的建模.同時,為了簡化分析過程,在建模過程中采用了6條通用的假設:(1) 同業務模式站點的數據到達率相等且服從相互獨立的泊松分布；(2) 不存在無限 buffer,緩存大小是相等的；(3) 只考慮由多普勒頻移造成的數據傳輸錯誤；(4) 站點的偵聽范圍和傳輸范圍相同；(5) 系統由一個 AP和多個 station組成,不考慮隱藏終端和暴露終端問題,故而數據傳輸只需考慮基本模式；(6) 任意站點發起數據通信時發生碰撞沖突的概率,與站點之前所處狀態無關.

2 Markov模型分析

定義二維隨機變量(s(t),b(t)),s(t)表示當前t時刻計數器所處的退避階數,b(t)表示當前t時刻計數器的值.根據上一節的分析假設,可以建立一個離散的二維馬爾可夫模型用于分析DCF機制的退避過程.如圖1所示.

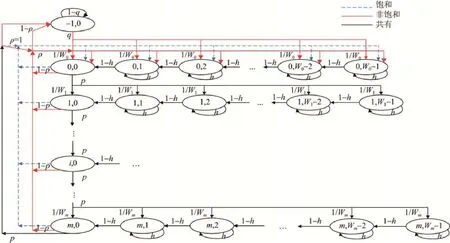
Fig.1 Markov chain model圖1 馬爾可夫鏈路模型

定義二維的平穩分布隨機過程bi,k=limt→∞P{s(t) =i,b(t) =k},i∈ [- 1 ,0,...,m]；k∈ [ 0,1,...,Wi- 1 ],其中,退避階數i表示由于之前過程中數據傳輸已經失敗了i次,當前處于等待發起第i次重新傳輸的隨機退避階段；退避計數器值k,為當前第i次重傳隨機退避過程中的退避計數器所記錄的值,m則表示定義的最大重傳次數值,m′是一個由最小和最大退避窗口大小所確定的值.其中,Wi可由式(2)確定.

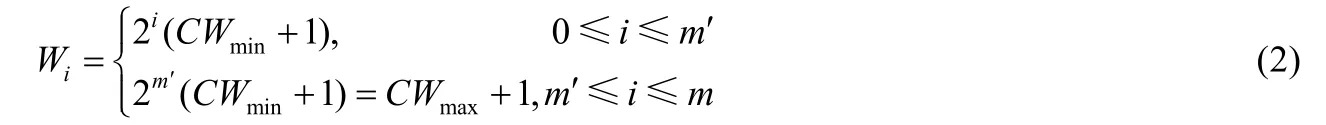
需要指出的是,狀態(-1,0)是非飽和工作站點的一個特殊狀態:當站點數據傳輸成功或達到最大重傳次數限制而丟包之后,有 1-ρ的幾率緩存中不存在數據等待發送,從而在接下來的一個時隙不能進入隨機退避過程.同時,在接下來的這一空閑時隙中,存在1-q的概率無數據達到,從而維持這一狀態,相反地,存在q的概率進入新的隨機退避過程.可以看出,本質上飽和工作模式下的DCF退避過程僅僅是非飽和工作模式下的一種特殊情況.

對于整個Markov模型,根據圖1,其一步轉移概率可歸納整理為

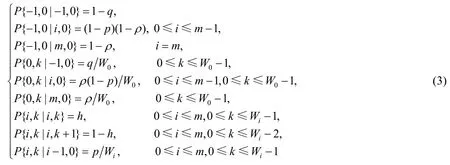
其中,p表示在數據發送的過程中由于數據碰撞或者數據傳輸錯誤而引起的傳輸失敗的概率；h是對于一個退避過程中的站點由于其他任意站點發起數據傳輸而造成其退避計數器凍結的概率.

由定義可知,當時間t→∝時,Markov鏈服從平穩分布,此時根據圖1、式(3)以及穩態過程中流出概率等于流入概率的邏輯關系,可得:

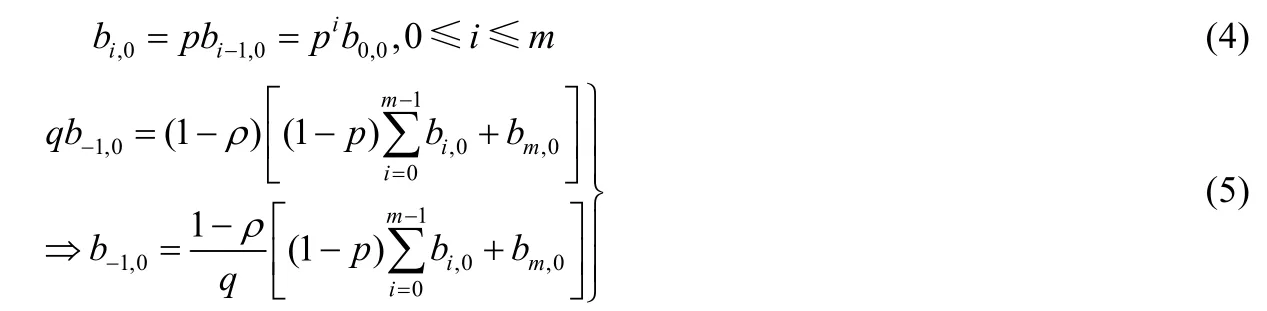
同時,狀態(i-1,0)到(i,k)的退避過程可表示為

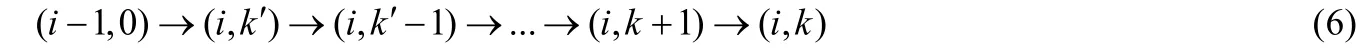
根據式(6)、圖1及流出概率等于流入概率,可進一步歸納分析得出二維穩態隨機變量bi,k與bi,0的邏輯關系:

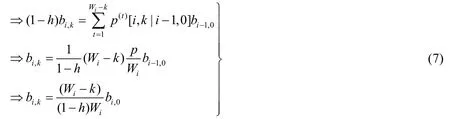
最后,根據Markov過程的歸一化條件可知:

聯立式(2)、式(4)、式(5)、式(7)以及式(8),可以解出狀態b0,0在任意時隙的傳輸概率為

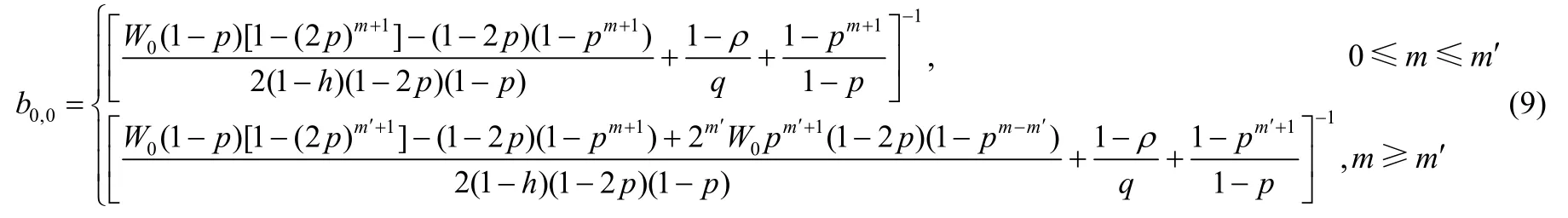
由式(4)、式(9)可歸納出任意工作模式站點在任意時隙有數據傳送概率的概率τ:

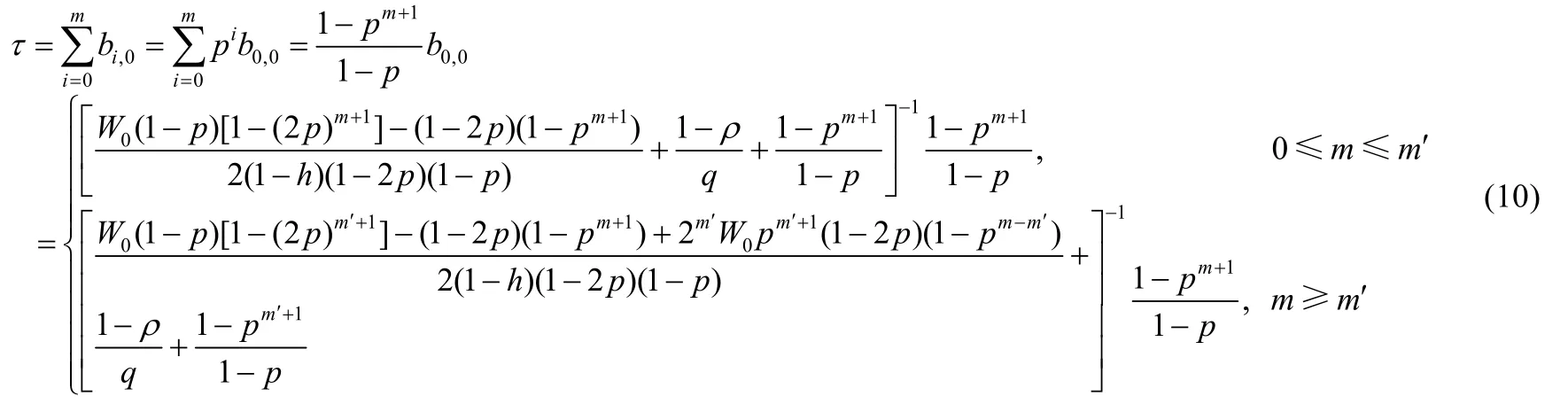
由討論可知,飽和模式是不飽和模式的一種特殊情況,即隨著站點不飽和概率的減少,站點將進入飽和工作模式,因此,此時ρ=1,且q=0.故對于飽和工作模式的站點,其任意時隙有數據傳輸的概率可以進一步寫作:

其中,飽和站點在任意時隙有數據傳輸的概率為τ′,傳輸失敗概率為p′,退避過程計數器凍結概率為h′.此時,在任意時隙有數據發送概率與Szczypiorski等人[20]提出的飽和算法模型中的數據發送概率是一致的.

3 異構網絡成分分析

3.1 異構模型概率分析

假設處于不飽和工作狀態的站點數為n,處于飽和工作狀態的站點數為n′,則對于指定的站點(非飽和或飽和工作站點),在其退避過程中,由于其他任意站點發送數據而造成退避計數器凍結的概率可以分別歸納為

其中,τ由式(10)確定,τ′由式(11)確定.同時,由文獻[11]可知,對于衰落信道,多普勒頻移造成的誤碼率FER及其引起的站點數據傳輸過程失敗的概率pe可分別表示為

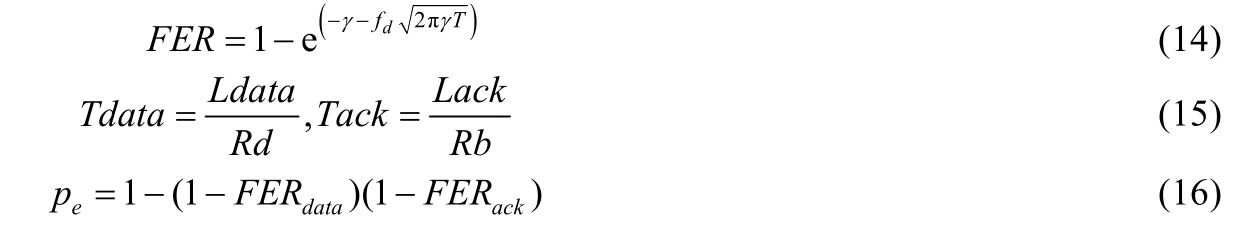
其中,γ是由接收機性能決定的陰影衰落余量,fd是通過移動速度與載波頻率計算出的最大多普勒頻率,T是由幀的大小及采用的傳輸速率所確定的幀傳輸時間.Tdata、Tack是數據幀及ACK(acknowledgment frame)幀分別采用數據傳輸速率Rd及基礎傳輸速率Rb傳輸所消耗的時間.因此,站點數據傳輸失敗的概率可分別寫作:

在任意時隙,有數據成功傳輸,可以認為有任意的唯一站點進行數據傳輸,其他站點都處于退避狀態或者(-1,0)狀態,且傳輸過程沒有發生幀錯誤.Ps、Ps′分別表示任意時隙有非飽和或飽和站點發送成功的幾率:

對于一個指定的節點(飽和或者非飽和節點),在其退避的過程中,偵聽到有任意站點成功傳輸數據的概率(受飽和節點或者非飽和節點分別是否有數據傳輸成功影響),故可根據式(19)、式(20)分別歸納為

對于任意時隙,不存在站點進行數據傳輸的概率可歸納為

一個指定的節點(非飽和節點或飽和節點),在退避過程中,偵聽到不存在其他站點發送數據的概率可表示為

3.2 狀態(–1,0)有數據包到達的概率

由于(-1,0)時隙極其短暫,能夠進入緩存的數據包個數遠小于2,結合M/G/1排隊模型[12],可以利用文獻[12]得出的M/G/1模型中的K=2時的情況對其進行準確、合理的分析,因此,此時有數據到達的概率可以歸納為

其中,λ是指站點的數據包平均達到率,是一個在相當長的時間段內確定的平均值；Eslot是一個僅對非飽和工作狀態的站點而言所定義的時間均值,由其他節點的3種工作狀態所確定的平均單位時隙的值.對于基礎模式有:

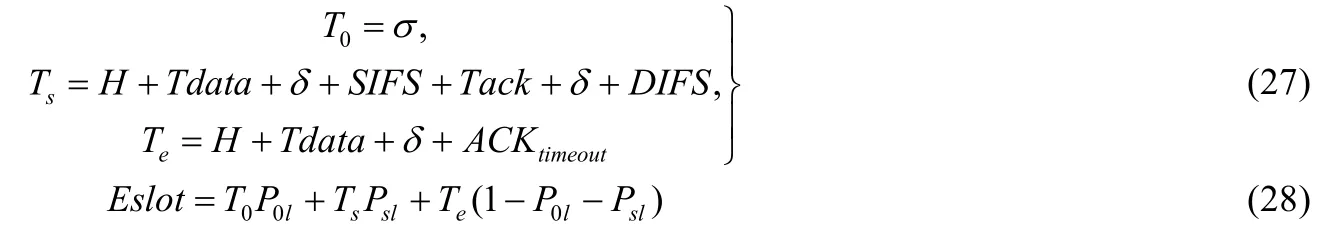
其中,T0、Ts、Te分別表示站點偵聽到其他任意節點處于退避狀態即無數據傳輸的空閑時隙大小、偵聽到有站點傳輸且成功所需等待的退避凍結時間、偵聽到有站點傳輸且失敗所消耗的退避凍結時間.H是所傳輸的幀的額外開銷,包括PLCP物理幀頭以及MAC幀頭的開銷；σ是IEEE協議定義的一個系統空閑時隙大小；δ表示信息傳輸過程中的時延；ACKtimeout是由于傳輸沖突或者傳輸錯誤造成的系統等待時間,對于基礎模式,兩者所需時間相等；SIFS(short inter-frame space)為協議設定的短幀間間隔.

3.3 非飽和站點完成一個周期的數據傳輸后有數據立即傳輸的概率

由文獻[11]討論的相關成果可知,站點完成一次數據傳輸后進入(-1,0)狀態的概率為 1-ρ,反之,開始新的隨機退避的概率為ρ,有:

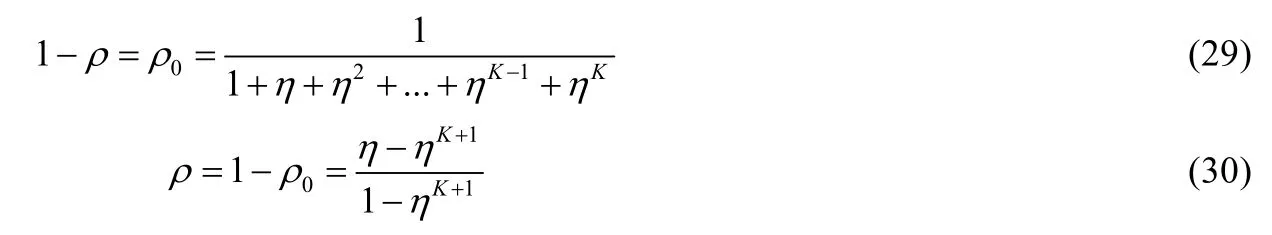
式中,η=λD,D是指一個數據發送周期的平均時長,即數據的平均服務時長,K表示緩存的大小.由圖1可知,一個服務周期的平均時長主要由3部分時間構成:成功傳輸所需的平均時間、成功傳輸前經歷的失敗過程所耗的平均時間以及退避過程中所花費的平均時間.同時,由第 1節討論分析內容可知,在退避過程中一個空閑時隙的等待時長是必然發生的.定義站點在退避過程中計數器減 1所需時間為Es,退避過程所消耗時間為Tbakoff,可得:

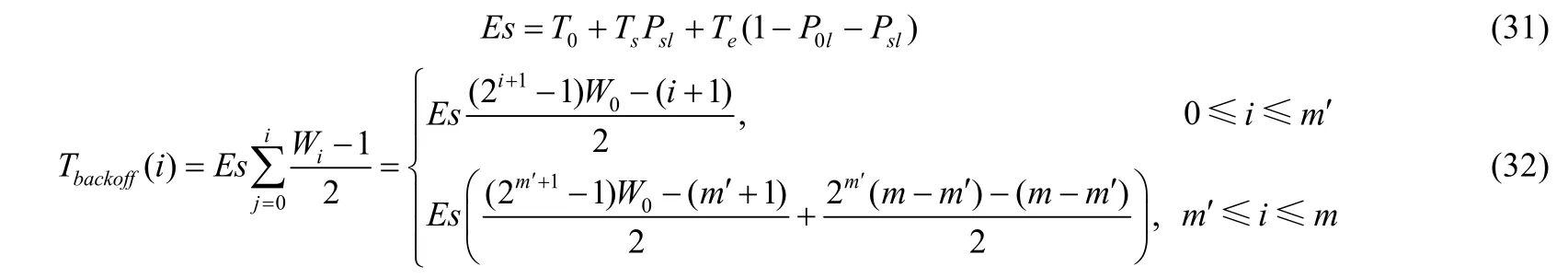
因此,非飽和工作站點的平均服務時長D可由成功傳輸過程中所消耗的加權均值時間與因重傳次數達到最大重傳次數限制且重傳失敗所花費的加權均值時間相疊加組成:

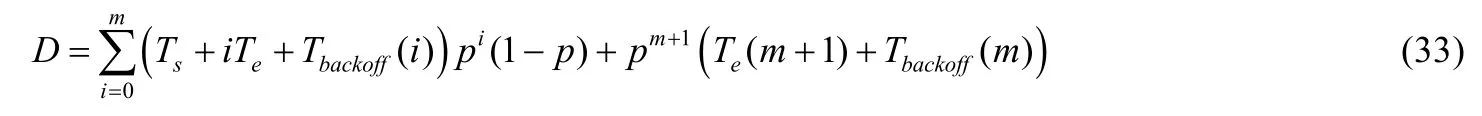
3.4 系統吞吐量

定義歸一化的系統吞吐量 TH(throughput)為任意單位時隙內任意站點發送的有效數據載荷E[d]與任意時隙的時隙均值E[s]的比值.吞吐量與節點數關系如圖2所示.

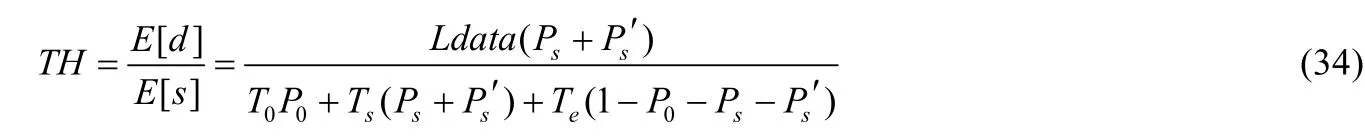
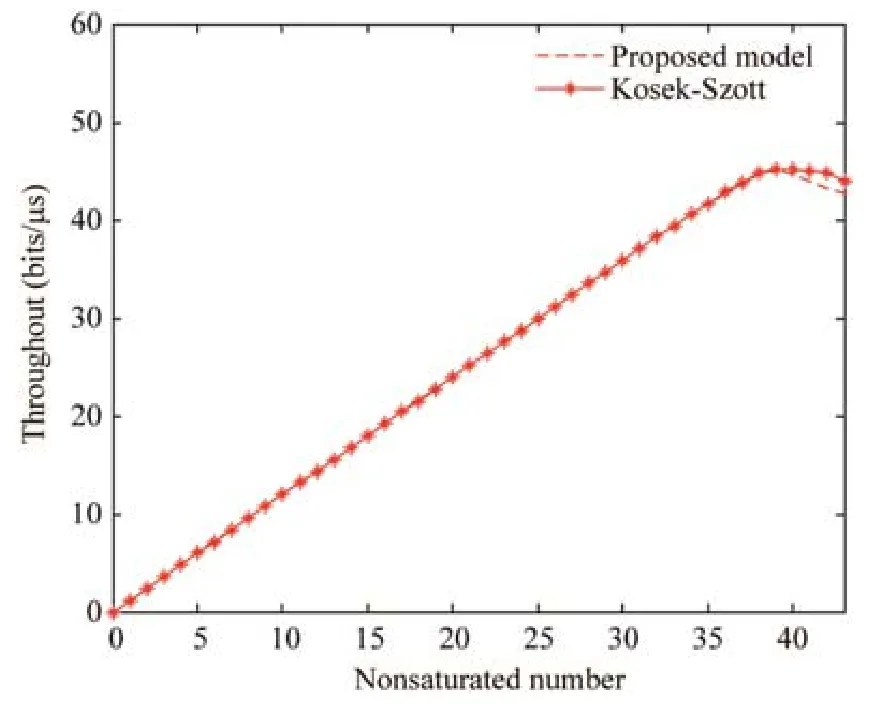
Fig.2 Throughput and number of nodes圖2 吞吐量與節點數關系

3.5 平均傳輸時延

定義平均傳輸時延為從站點進入退避過程開始,到成功收到接收站點回復的ACK確認幀,確認數據成功傳輸為止,為數據的傳輸時延,即一次成功的數據通信所消耗的平均時間.與式(33)相似,可以分別歸納出非飽和站點及飽和站點的平均傳輸時延:

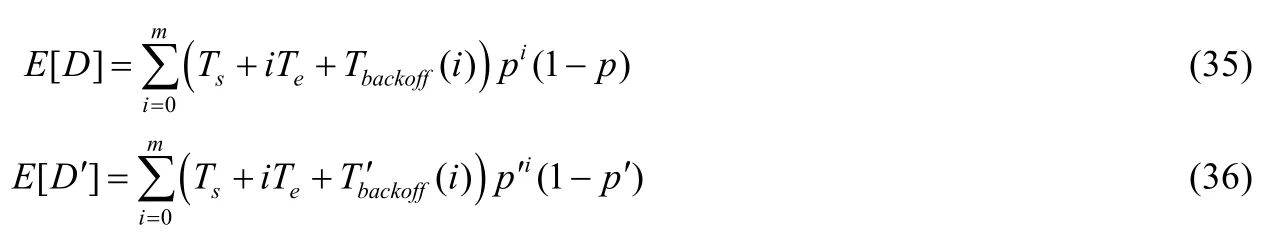
3.6 傳輸丟包率

由于數據到達率服從泊松分布,且緩存狀態與之前狀態過于相關,故服務時長內緩存溢出丟包率的是極其復雜的,只考慮當前狀態而不考慮之前狀態是不準確的.因此本文只討論給出了由于站點達到最大重傳次數限制而丟包的傳輸丟包率,對于非飽和工作站點及飽和工作站點的傳輸丟包率可分別表示為

4 數值分析及仿真實現

仿真的參數來源于IEEE 802.11ac[2]協議的相關部分,見表1.需要特別指出的是,在進行算法比較時,不同模型間的對比將采用包括但不限于對算法部分內容進行置零等方法,使提出的算法與對比算法在參數及變量上保持一致,以盡可能地消除不必要的干擾.

Table 1 Summary of IEEE 802.11ac parameters表1 IEEE 802.11ac DCF參數設置

本文提出的算法在圖 2中與 Kosek-Szott[19]提出同樣聚焦于異構混合成分網絡的算法進行了對比.在仿真的過程中提出的算法在參數設置上與文獻[19]完全相等,即不考慮最大重傳次數大于最大窗口的階數,不考慮誤碼率等情況.同樣地,與文獻[19]中討論的方式相同,為了便于仿真以及增加多組對比,只對非飽和工作模式下的DCF模型進行了分析比較.結合文獻[19]中的相關成果,可以得出,在不飽和節點逐漸增多的過程中,由于傳輸碰撞概率的增加不飽和性減小而飽和概率增加,提出的算法結果優于文獻[19]中的結果,更接近于 DCF機制的實際吞吐量,這主要得益于概率歸納更準確以及服務時長考慮更完善.同時,在建模過程中,本文提出的算法對不飽和性的計算是通過概率的大小來表示的,故在算法實現的過程中,隨著不飽和節點數或數據包達到率的增加可以自動同步計算新的不飽和性.而文獻[19]中的算法由于其采用的是M/M/1/K排隊模型,且在不飽和性的處理上將其與單位時隙平均達到的數據包個數相等同,因此,隨著系統趨于飽和,需要計算不飽和模式與飽和模式之間的連接點并適時地利用飽和算法來計算飽和模式下的任意時隙有數據發送的概率.因此,這種算法相對提出的算法更加復雜,且文獻[19]中數據包達到率被定義為服從泊松分布,因此,簡單地用平均值來處理系統不飽和性的方法也是不太準確的.

在圖3和圖4中,提出的算法與兩種只聚焦于同質網絡成分的算法在相同參數條件下進行了仿真比較.

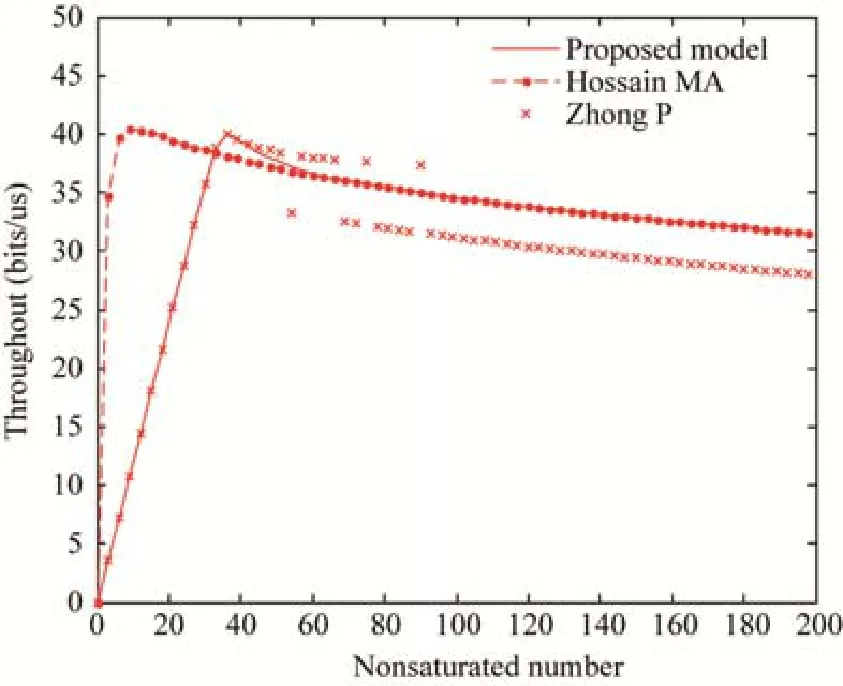
Fig.3 Throughput and number of nodes (m＞m′)圖3 吞吐量與節點數關系(m＞m′)

相較于Hossain等人[11]提出的算法,由于本文充分考慮了數據排隊等待的不同狀態時長,分別給出了不同q值和ρ值,而文獻[11]中簡單地將二者等同,故而在系統進入飽和前,提出的算法對非飽和狀態的結果處理得更好,與 Zhong等人[21]提出的算法仿真結果趨于一致,而文獻[21]中的成果同樣驗證了這一結果是準確的.但是隨著不飽和節點的增加,系統進入飽和狀態,提出的算法與文獻[11]中的算法仿真結果保持一致,反觀文獻[21],由于模型穩態求解的結果有誤,以及對退避過程考慮不夠全面,當m＞m′時,仿真結果出現劇烈的波動；當m=m′時,3種算法仿真結果保持基本一致.

Fig.4 Throughput and number of nodes (m=m′)圖4 吞吐量與節點數關系(m=m′)

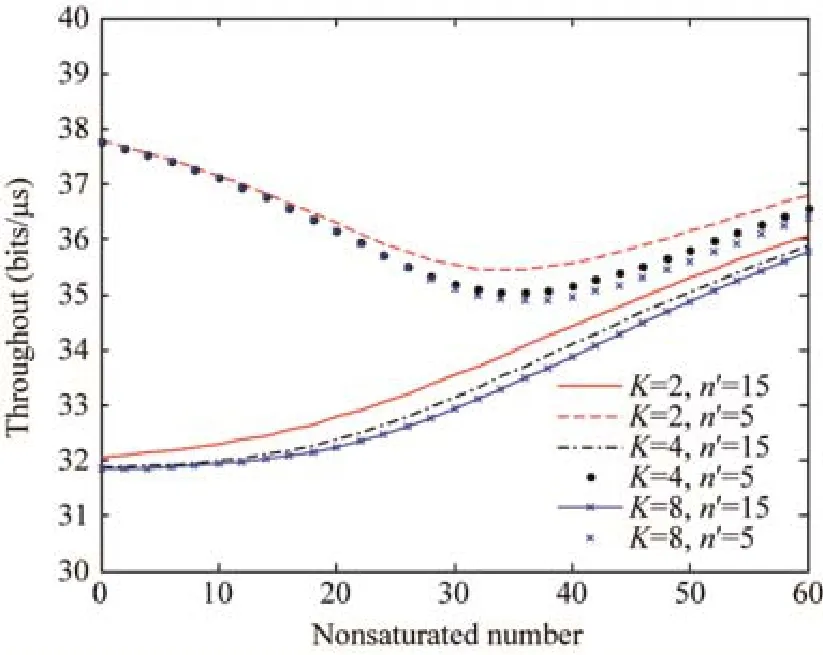
Fig.5 Throughput under heterogeneous traffic sources圖5 異構業務下的吞吐量

因此,相較于文獻[11,19,21]中的算法,本文提出的算法更加準確、全面,同時保持了相對的簡單.故而能夠更好地模擬與分析包括單一的同質網絡業務成分和異構網絡業務成分在內的IEEE 802.11 DCF機制的性能.

圖5～圖7中利用提出的算法對異構網絡業務進行了綜合性仿真,分別給出了不同大小的緩存K值、飽和節點數n′隨著不飽和節點數n的增長與系統吞吐量、傳輸時延及傳輸丟包率的關系.

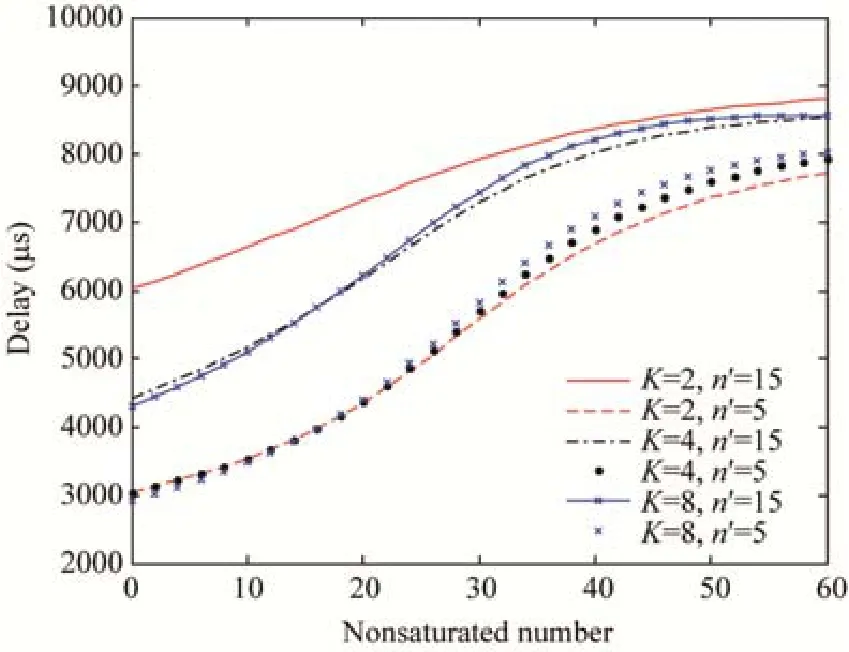
Fig.6 Delay under heterogeneous traffic sources圖6 異構業務下的傳輸時延

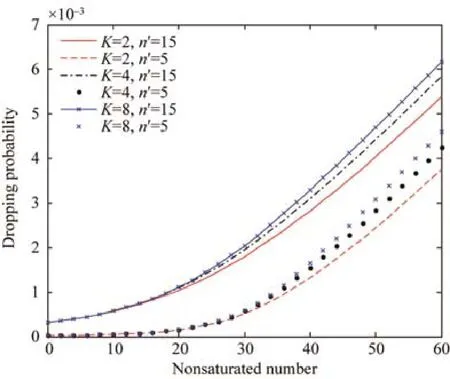
Fig.7 Dropping probability under heterogeneous traffic sources 圖7 異構業務下的傳輸丟包率

可以看出,當飽和節點數n′一定時,吞吐量會隨著K值的增長而降低,這是由于K值的增加導致非飽和節點任意時隙發送幾率隨之增加,從而導致吞吐量一定程度的下降；同樣地,傳輸時延將在一定程度和范圍內出現增加.當K值一定時,隨著飽和節點數的增多,吞吐量由于系統過于飽和導致沖突可能性的激增,進而導致吞吐量的減少,伴隨著不飽和節點的增多,飽和性能被稀釋,逐漸進入非飽和階段,吞吐量重新進入增長期,直至進入新的飽和狀態,再隨節點數的增加而減少；同時,由于網絡中節點數的增長,數據碰撞概率增加,傳輸時延跟隨不飽和節點數的增長而增加.對于傳輸丟包率,隨著節點數的增加,傳輸丟包率趨于指數型增長.同時,隨著K值的增加,丟包率也會出現輕微的增加.

5 結 語

本文提出了一種改進的全新混合Markov模型,詳細分析了模型中的不同變量和概率,給出了相應的改進計算方法.結合M/G/1排隊模型,以及對有錯信道的思考,全面考慮了IEEE 802.11 DCF機制中的退避凍結及重傳限制等,在保持模型簡單的同時,能夠準確地分析緩存大小、節點數量、包到達率等關鍵問題與系統吞吐量以及時延的關系.通過仿真與分析可以得出,本文提出的算法模型與現有算法模型相比,不僅能夠更好地對異構混合業務進行合理的建模、分析,而且更加準確、簡單；同時,在單一業務的工作模式下(即將另一種業務的任意時隙的發送概率置零的情況下),本文提出的算法與DCF機制仍然保持了較好的一致性.

在接下來的工作中,將進一步完善相關模型,以及對文獻[22]中提到的公平性等問題進行合理、有效的討論,同時,聚焦于對新的隨機接入方式TF-R(trigger frame for random access)[23]進行分析與研究.在提出的模型上,將DCF與 TF-R接入方式進行聯合建模,從而對 IEEE 802.11ac與 802.11ax混合模式場景下的性能進行有效的分析.

Table A表A

Table A (Continued)表 A(續)