方程思想漫談
——以北師大版四下“認識方程”為例

□王林

小朋友，方程思想是數學中的一種重要思想，在用這種思想解題時，從分析問題的數量關系開始，找出已知量與未知量之間的關系，用字母表示未知數，列出方程，并解方程，讓問題得以解決。這種思想在生活中隨處可見，不信？請看：

例1奶奶今年57歲，孫子今年5歲。再過多少年，奶奶的年齡是孫子的5倍？

［分析與解］無論過多少年，奶奶與孫子的年齡差是不變的。不妨假設再過x年，奶奶的年齡是孫子的5倍，這樣就可以建立等量關系式：奶奶今年的年齡+再過的年數=（孫子今年的年齡+再過的年數）×5。

解：設再過x年，奶奶的年齡是孫子的5倍，則奶奶今年的年齡+x=（孫子今年的年齡+x）×5。

列出方程如下：

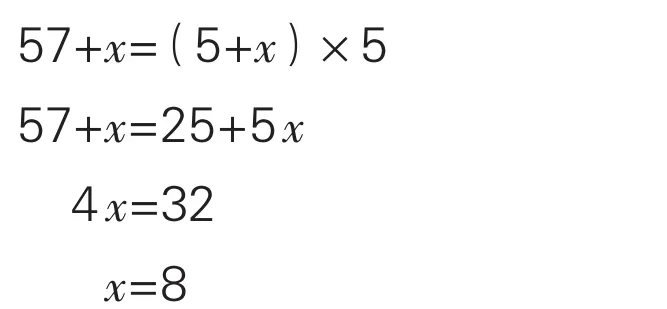
答：再過8年，奶奶的年齡是孫子的5倍。

例2在雙軌鐵道上，行駛著兩列火車，在前面的是一列長300米的和諧號列車，在后面的是一列長200米的復興號列車。復興號超過和諧號一共用了125秒。復興號每秒行駛27米，你知道這列和諧號列車此時的速度嗎？

［分析與解］兩列火車、超車、只知道一列火車的速度……想不“蒙”都有些難，一切似乎都在變，都不穩定。不要著急，有變就有不變。不變的在哪里呢？找找看，比如，兩列火車的車身長有沒有變？對了，沒變！

看準聯系，運用方程思想解決問題。當復興號超過和諧號時，此時一共比和諧號多走了300+200=500（米）（想想為什么）。換句話說，就是復興號在125秒的時間里，比和諧號多走500米。

和諧號的速度+復興號每秒比和諧號多走的米數=復興號的速度解：設和諧號每秒行駛x米。