封隔器膠筒變形穩定性分析*

張付英 張玉飛 李天天 水浩澈 董城城 楊俊梅

(1.天津科技大學機械工程學院 天津 300222；2.天津市輕工與食品工程機械裝備集成設計與在線監控重點實驗室 天津 300222)

封隔器膠筒是井下油氣分層鉆采工藝的關鍵密封零部件，通過依靠管柱壓重或水力載荷壓縮膠筒，從而封隔環形空間實現密封。隨著能源供給結構的調整和對油氣需求的增加，封隔器膠筒的設計研究也日漸深入。 由于封隔器工況環境惡劣，膠筒在整個密封過程中的狀態及變形都可能對材料造成破壞及影響密封性能。因此膠筒的穩定性問題受到極大關注。

提高材料穩定可靠性，降低因不穩定性帶來的社會、環境和經濟等效益損失，一直是專家學者研究的重點。超彈性材料的穩定性研究，最早是EULER于1774年發表的關于彈性曲線的研究[1]。此后諸多專家學者進行深入研究，如李旭和竇益華[2]分析了膠筒變形階段其絕對體積變化規律，確定了膠筒最小坐封載荷和約束壓力，解釋了膠筒坐封時損壞的原因；任九生和程昌鈞[3]應用有限變形彈性理論，分析了受內壓和拉伸作用的超彈圓筒發生非均勻變形的不穩定問題；郭易和劉博[4]選取不同尺寸圓筒試件，通過試驗檢測、理論計算和有限元分析，對各理論與試驗結果進行了契合比較，試圖找出一種能準確推斷圓筒結構失穩載荷的理論方法；GELLIN[5]通過建立管道截面的應變-位移關系，對無限長管在彎曲作用下的失穩和極限承載力進行了研究。任九生和程昌鈞[6]綜述了Rivlin立方塊問題、薄壁球殼和圓柱扭轉問題、空穴生成問題等超彈性材料中材料不穩定問題的最新進展成果，闡述了各種非線性不穩定問題的特點、求解以及研究方向。鄭明軍、史守峽等[7-8]應用有限元對橡膠件的變形階段進行了相關研究。

目前對封隔器膠筒變形過程的穩定性研究主要集中于數值計算，應用有限元模擬膠筒不穩定變形等相關問題的研究還未深入。因此，為了模擬封隔器膠筒在實際工況下的不穩定變形過程，本文作者分析了膠筒在初始狀態時，在軸向載荷作用下不同橡膠材料在不同高徑比的不穩定變化過程，研究結果對膠筒材料及參數的選擇提供了參考。

1 模型建立及變形過程

1.1 膠筒結構的有限元模型

作為封隔器中關鍵的密封元件，其密封性能直接影響井下工作的安全與開采效率。隨著完井鉆探技術的提高，相應地對密封材料的性能提出了更高要求，近年來應用較為廣泛的膠筒材料有丁腈橡膠(NBR)、氫化丁腈橡膠(HNBR)、氯丁橡膠(CR)、聚四氟乙烯(PTFE)、氟橡膠(FKM)和聚氨酯橡膠(PU)等。文中選擇NBR、HNBR、FKM和PU 4種材料進行研究，建模過程中膠筒的材料模型采用Mooney-Rivlin模型。各種材料的Mooney-Rivlin系數如表1所示。

中心管、套管、壓環等材料均采用40CrMnMo，彈性模量為206 GPa，密度為7.85 g/cm3，泊松比為0.25。由于其變形量較小，因此可近似為剛性，膠筒與中心管、套管等之間的接觸視為剛性與柔性的接觸。膠筒接觸面作為分析的柔性從表面，其網格劃分比剛性主表面較為嚴格質密[9]，因此膠筒網格劃分采用四結點雙線性軸對稱四邊形CAX4RH單元，而中心管、套管等以CAX4H為單元劃分網格。

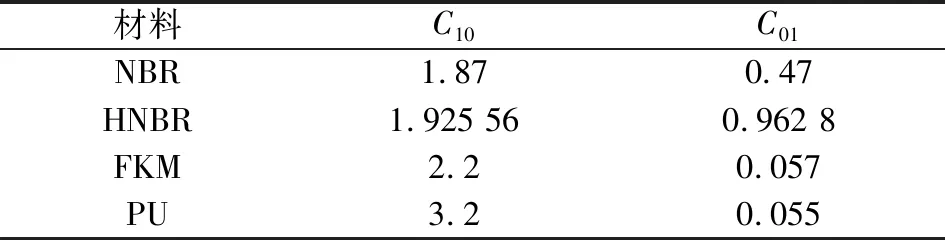
表1 材料屬性

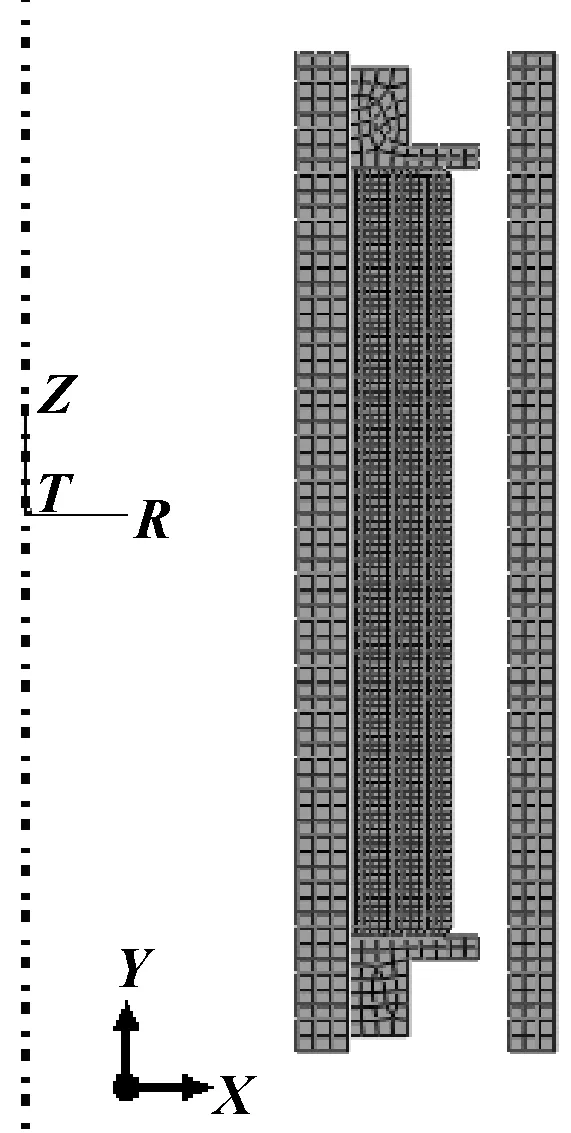
圖1 膠筒結構有限元模型

1.2 膠筒變形過程

初始安裝的封隔器膠筒在井下處于無壓縮狀態。在軸向壓縮力作用下，膠筒體積的不可壓縮性使膠筒在徑向發生膨脹變形，膠筒側面未與套管內壁接觸前屬于自由穩定變形(如圖2所示)，該變形階段是膠筒由靜態平衡向動態平衡轉變的開始，同時也是膠筒在無約束變形過程中，最容易發生不穩定變形的階段(如圖3所示)。

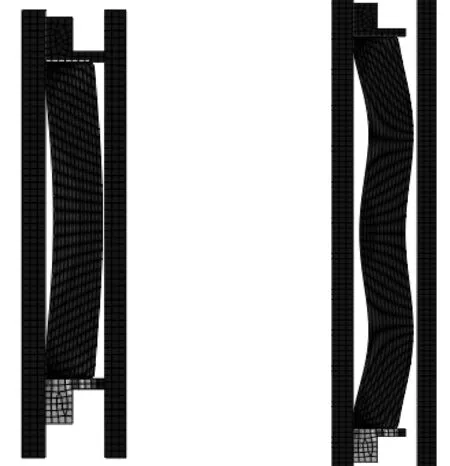
圖2 自由穩定變形 圖3 自由不穩定變形

當自由變形到達膠筒側面與套管和中心管接觸時，膠筒因受到套管和中心管的限制而發生約束變形。膠筒首先與套管內壁接觸，隨著軸向力的增加接觸面也隨之增大；但在約束變形過程中，如果膠筒的密閉接觸面是由中間向上下兩邊延伸(如圖4所示)，則是約束穩定變形；若膠筒接觸面之間出現環空的未接觸空間(如圖5所示)，則是膠筒發生約束不穩定變形，再繼續施加適當載荷后，膠筒逐漸形成穩定變形。該階段的膠筒不僅受到軸向載荷力作用，還受到套管及中心管約束而產生的接觸應力和庫侖摩擦力作用，由于膠筒材料的特殊性，膠筒變形呈現非線性變化，體應變不為0。

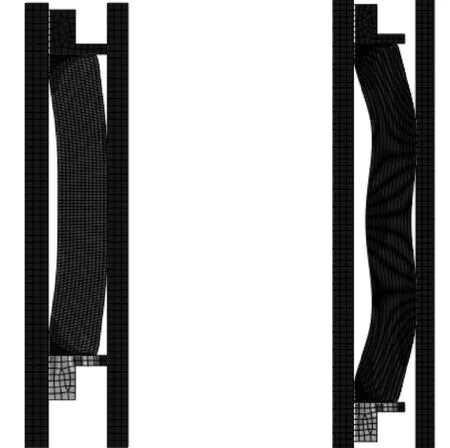
圖4 約束穩定變形 圖5 約束不穩定變形圖

在膠筒約束變形階段基礎上，施加工作載荷，膠筒的變形逐漸過渡到穩定變形階段。穩定變形階段的膠筒變形仍是非線性的，其絕對體積也發生了變化。

2 膠筒的變形分析

橡膠與類橡膠材料的力學性能復雜，如天然橡膠、合成橡膠、合成纖維等都具有非線性、高彈性和大變形等顯著特點[10]。一定環境和載荷下，彈性體材料都會存在變形、失穩、破壞及使用壽命等問題，膠筒作為關鍵的密封部件，研究其材料和結構變形的不穩定性對后續材料損傷和疲勞破壞的研究具有重要作用。

2.1 自由變形分析

膠筒自由變形階段，膠筒端面受到軸向載荷作用而逐漸膨脹變形，向套管內壁靠攏。但在膠筒外側面未與套管內壁接觸前，不同高徑比或材料性能的差異使膠筒側面在自由變形階段出現分化：如圖6所示的情況，膠筒變形是以平穩“拋物線”的形式向穩定變形的方向發展；如圖7所示的情況，由于膠筒高徑比的增大，使膠筒筒身受力不均而導致其側面以“馬鞍型”不穩定波動變形。兩種分化現象屬于膠筒同一變形階段下的兩種不同表現形式。

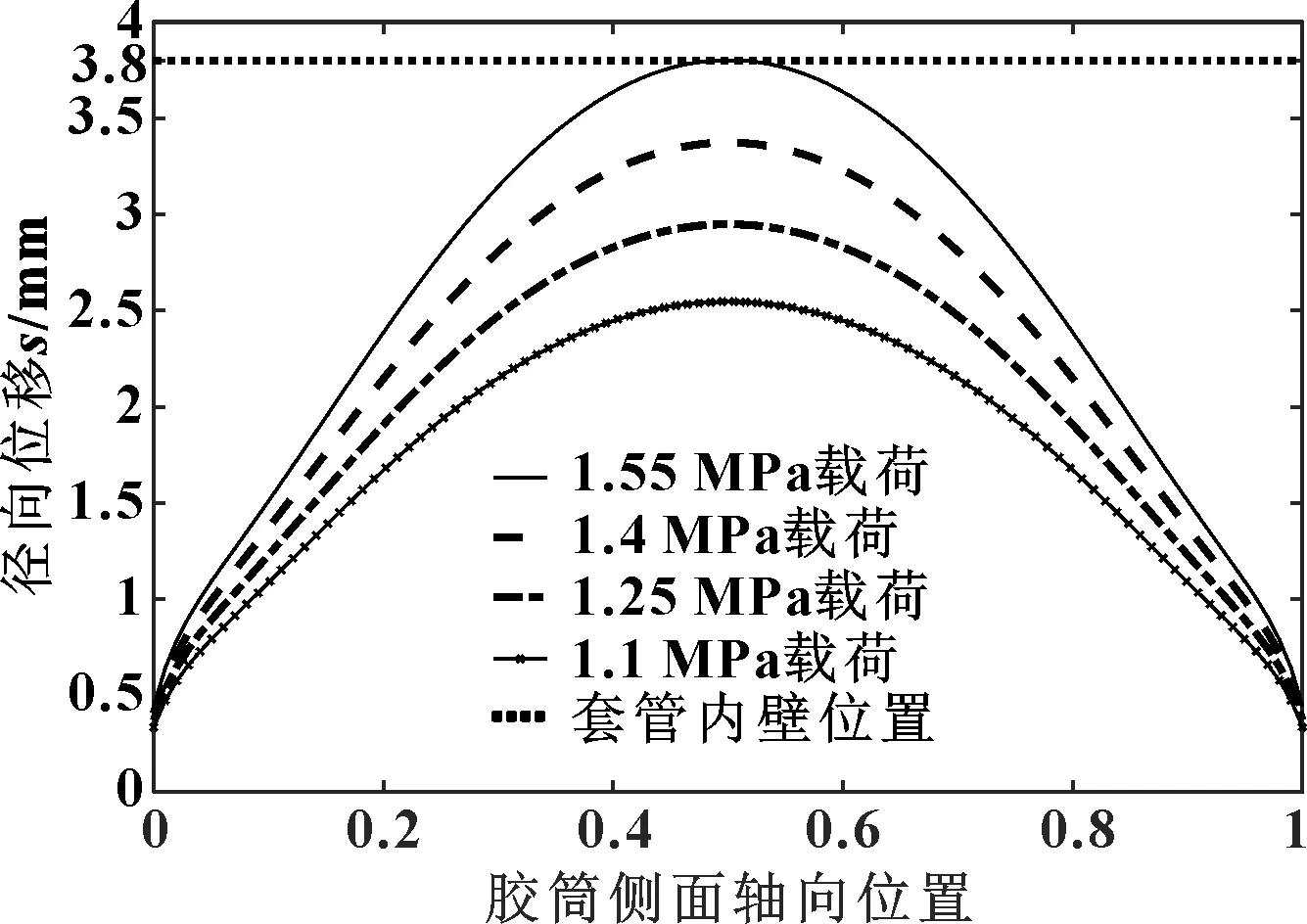
圖6 自由穩定變形的位置-位移圖(高徑比為0.901)

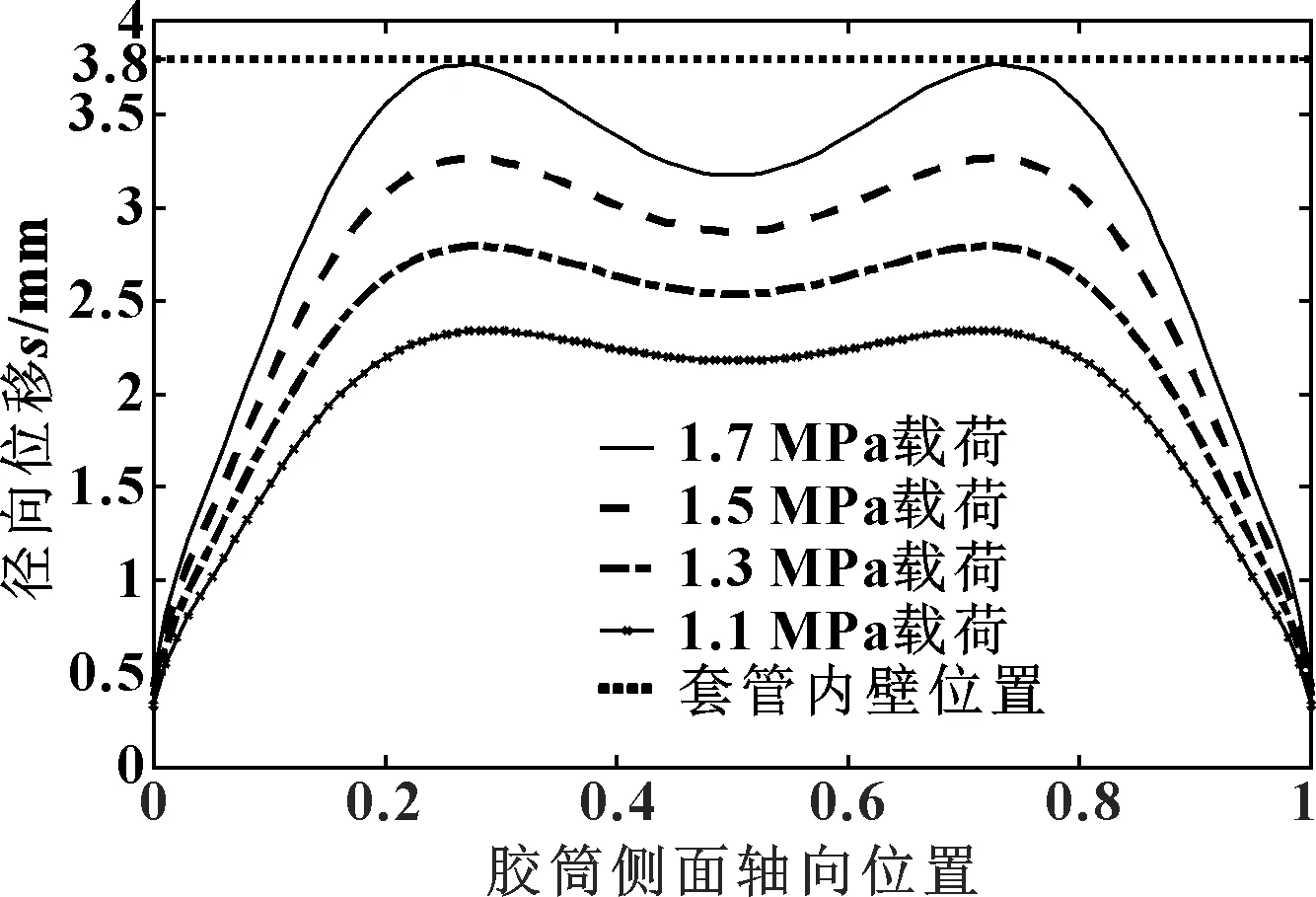
圖7 自由不穩定變形的位置-位移圖(高徑比為1.622)

如圖6所示為膠筒高徑比取0.901，材料選擇HNBR時，在不同載荷下的變形位置與位移關系。隨載荷增大，膠筒徑向最大變形位移逐漸靠近套管內壁位置，但膠筒始終表現出穩定的形變過程。這是由于高徑比在一定范圍時，膠筒兩端受到一對相反的作用力，膠筒最大變形沿筒高出現在膠筒中部位置，使膠筒發生屈曲變形。

當膠筒高徑比高于某一特定值后，由于筒身受力情況的變化，膠筒側面最大變形位置由原來的中部一個點變為兩個點，致使膠筒的自由變形過程出現了“馬鞍狀”的不穩定形狀，如圖7所示為HNBR材料的膠筒在高徑比為1.622時的變形圖。可見， 在該高徑比下，不同載荷值都會使膠筒的變形呈現出較明顯的不穩定變形現象，變形曲線都有兩個峰點和一個谷點，谷點位置位于膠筒的中部，兩個峰點以中部位置為中心，左右對稱分布。

當膠筒側面任意位置剛剛接觸到套管內壁時，膠筒自由變形階段即結束，其繼續變形會受到套管的約束。因此，為了研究HNBR膠筒的高徑比變化對初封需要施加的載荷的影響，文中在高徑比0.901～2.252范圍內，對使膠筒與套管能夠實現剛剛接觸所需要的最小施加載荷進行了分析，結果如圖8所示。顯然，膠筒高徑比在0.901～1.342范圍內時，膠筒外側面與套管內壁接觸所需的最小軸向載荷隨高徑比的增大而升高；高徑比在1.468～1.73時，需要施加的最小載荷隨高徑比的增大而降低；當高徑比在1.342～1.468與1.73～2.252之間時，膠筒與套管接觸所需的最小施加載荷是不變的，分別是1.75和1.7 MPa，其值不隨高徑比變化而變化。表明膠筒高徑比對所需剛好使膠筒與套管實現接觸的最小載荷是有影響的，但影響的效果不是線性的，不同高徑比區間所需要的使膠筒與套管接觸的最小載荷是不同的。

常用的密封材料有橡膠、塑料、石棉-石墨、金屬等，用于高壓完井的聚合物密封材料又分為合成橡膠、熱塑性塑料和熱固性塑料。為了研究材料差異對膠筒變形過程的影響，圖8中還對常用的HNBR、NBR、FKM、PU 4種膠筒材料，在不同高徑比下使膠筒和套管剛好接觸所需要的最小載荷進行比較，如圖8所示。

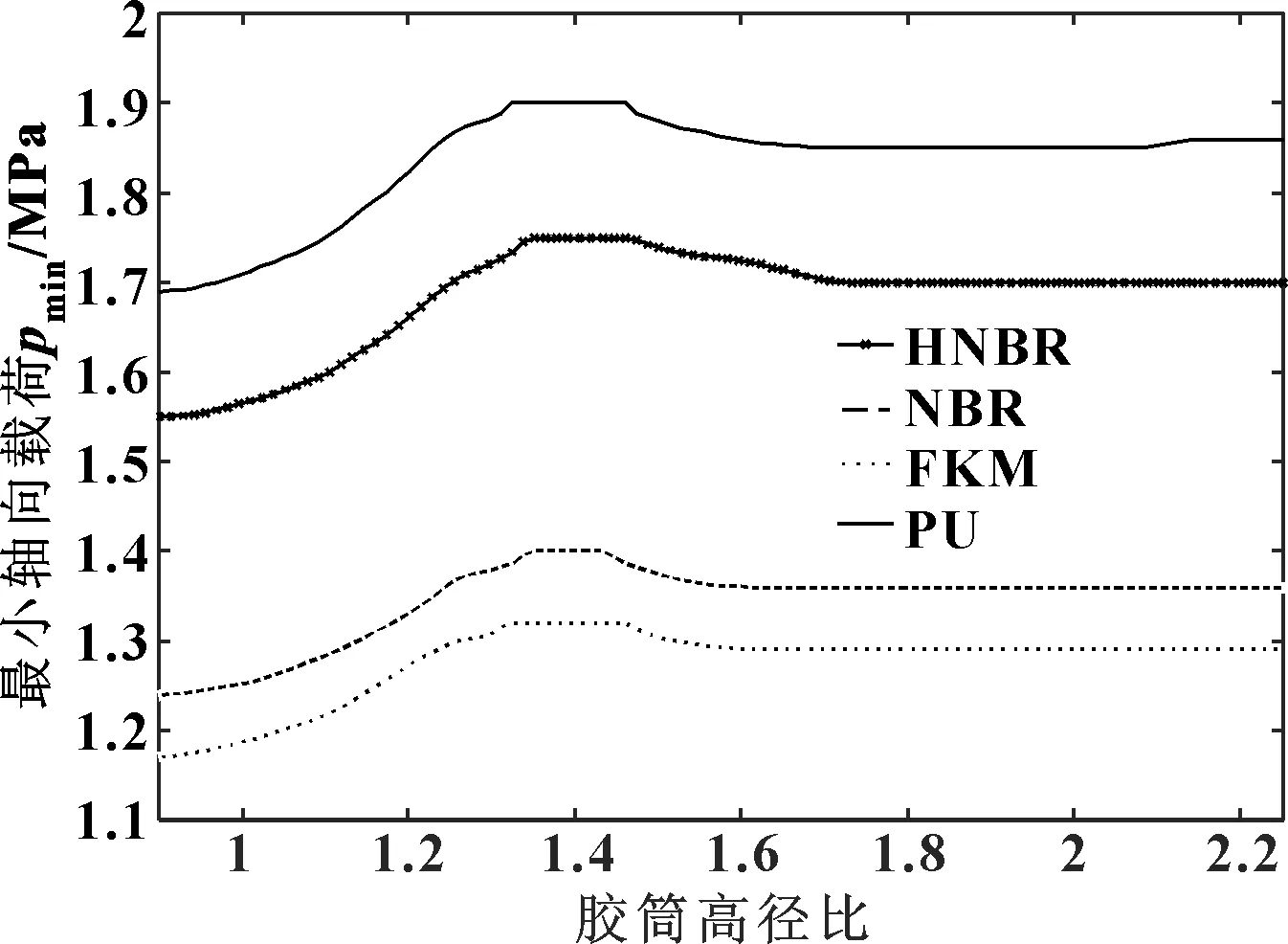
圖8 高徑比與最小軸向載荷關系

顯然，膠筒采用不同的材料會對膠筒變形過程產生不同的影響。4種材料的高徑比與使膠筒和套管剛好接觸所需要的最小載荷關系曲線變化趨勢大致相同，但每種材料使膠筒和套管剛好接觸所需要的最小載荷隨高徑比變化有所不同。這表明高徑比變化時，材料的差異對使膠筒和套管剛好接觸所需要的最小載荷的變化趨勢影響不明顯，但對使膠筒和套管剛好接觸所需要的最小載荷的取值有顯著影響。4種材料中，PU材料使膠筒和套管剛好接觸所需要的最小載荷的值最高，然后依次是HNBR、NBR和FKM。

2.2 約束變形分析

約束變形階段，膠筒由于受到套管內壁限制，隨著軸向載荷的增加，膠筒與套管的接觸面積逐漸增大。與自由變形相似，此過程同樣會由于高徑比與材料的差異使膠筒的變形出現穩定和不穩定兩種分化現象，約束穩定變形是指在膠筒最大變形點處，膠筒與套管內壁接觸后，在軸向載荷作用下，膠筒側面的接觸面平穩向兩側延展。如圖9所示為膠筒材料為HNBR，高徑比取0.901時膠筒的約束變形，在逐步施載過程中，膠筒始終保持穩定的形變過程，在套管約束作用下，也未出現失穩現象。穩定變形對膠筒使用壽命和密封性能具有十分重要的意義。

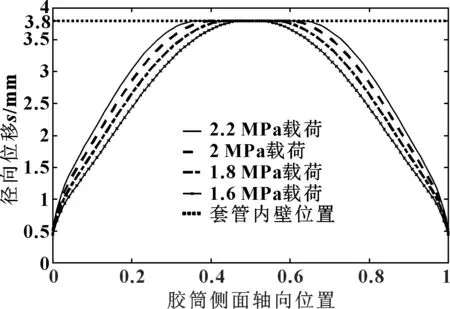
圖9 約束穩定變形位置-位移圖(高徑比為0.901)

約束不穩定變形是指膠筒中部位置的最大變形與套管內壁實現接觸后，隨軸向載荷的增加，膠筒最大變形位置從中心位置沿軸向向上和向下兩個位置移動，使變形曲線形成兩個峰點和一個谷點。兩個峰點處膠筒與套管接觸，而谷點處膠筒未與套管接觸，此變形過程會使膠筒受力不均，因而對膠筒損傷較大。因此需繼續施加軸向載荷以消除不穩定性變形，使膠筒側面的谷點變形接觸到套管內壁，確保膠筒變形進入穩定約束變形階段。

如圖10所示為膠筒材料選用HNBR，高徑比取1.622時膠筒的變形情況。顯然，膠筒從不穩定變形過渡到穩定變形是一個漸變過程，當軸向載荷到達某一臨界值時，膠筒不穩定變形消失。

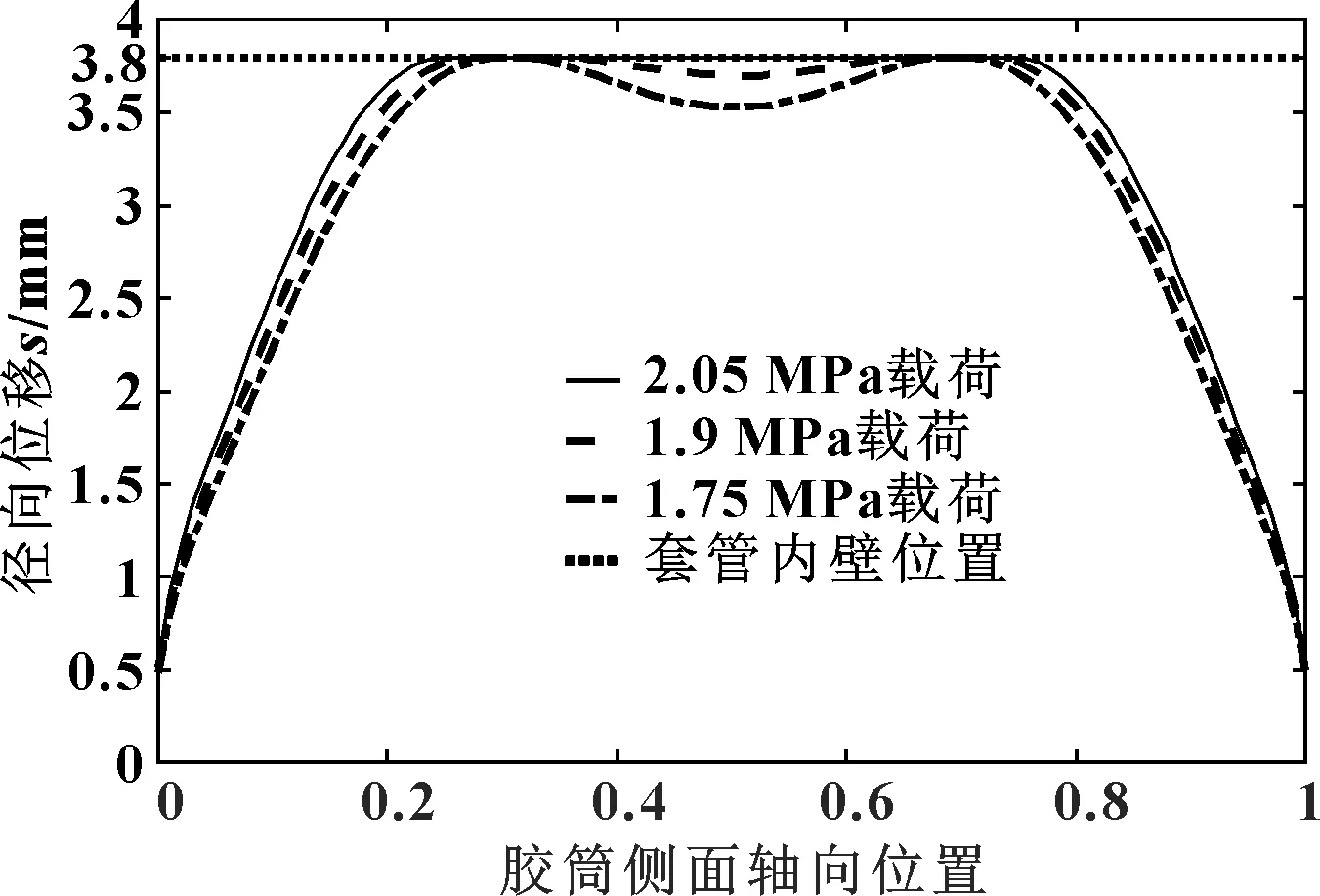
圖10 約束不穩定變形位置-位移圖(高徑比為1.622)

為了探索高徑比變化過程中，膠筒從不穩定變形過渡到穩定變形所需的臨界載荷，文中對HNBR、NBR、FKM和PU 4種膠筒材料，在高徑比0.901～2.252范圍內的膠筒變形進行了分析，結果如圖11所示。

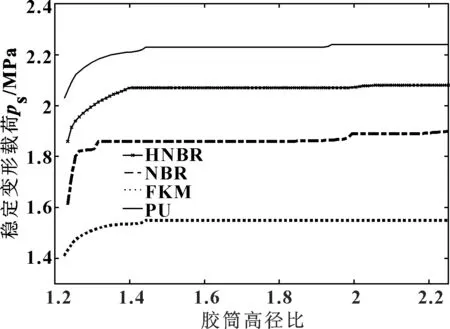
圖11 高徑比與穩定變形載荷關系

以HNBR為例，膠筒的高徑比小于1.234時，膠筒變形始終是穩定的，其變形不會隨高徑比或載荷力的變化而發生不穩定變形的情況；只有當膠筒高徑比大于1.234時，膠筒才會在載荷作用下發生不穩定變形，且隨高徑比的變化，膠筒從不穩定變形過渡到穩定變形所需的載荷值會有所不同。高徑比在1.234～1.405范圍內，膠筒從不穩定變形到達穩定變形所需的載荷值隨高徑比的增大而增高；高徑比在1.405～1.982范圍內時，膠筒從不穩定變形過渡到穩定變形而所需的載荷值穩定為2.07 MPa；當高徑比大于1.982后，膠筒達到穩定變形所需要的載荷值稍有升高，但在高徑比大于2.072后，達到穩定變形所需的載荷值保持在2.08 MPa且其值不再變化。

圖11還表明，4種材料的高徑比與使膠筒到達穩定變形的載荷關系變化趨勢大致相似，因此可認為材料差異對使膠筒實現穩定變形的載荷變化趨勢影響不大，但對從不穩定變形達到穩定變形所需的載荷值的大小有顯著影響。4種膠筒材料中，PU達到穩定變形所需載荷最高，FKM最低。且HNBR與NBR在高徑比小于1.234，FKM與PU在高徑比小于1.225時，不會出現膠筒不穩定變形的情況。當4種材料隨高徑比變化發生約束不穩定變形時，從不穩定變形過渡到穩定變形所需要的載荷值逐漸增大；在到達某一特定值后，膠筒所需要的穩定變形載荷將基本保持不變，不再隨高徑比變化而出現較大波動。

3 結論

(1)由于高徑比與材料的差異，膠筒在自由變形與約束變形階段都會出現穩定變形與不穩定變形兩種分化現象。自由穩定變形階段膠筒隨載荷的增加，膠筒側面變形以“拋物線”的形式逐步向套管內壁靠近；自由不穩定變形階段膠筒側面呈現“馬鞍形”的變形曲線形狀。

(2)HNBR膠筒在自由變形階段，高徑比在0.901～1.342時，使膠筒側面與套管接觸的最小軸向載荷隨高徑比的增大而增大；高徑比在1.468～1.73時，使膠筒側面與套管接觸的最小軸向載荷隨高徑比的增大而降低；當高徑比在1.342～1.468與1.73～2.252范圍時，使膠筒側面與套管接觸的最小軸向載荷值分別為1.75和1.7 MPa。表明膠筒高徑比會影響使膠筒側面與套管接觸的最小軸向載荷，但影響的效果不是線性的，不同高徑比區間所需要的使膠筒側面與套管接觸的最小軸向載荷是不同的。

(3)HNBR膠筒在約束變形階段，當高徑比小于1.234時，膠筒的變形始終穩定；當膠筒高徑比大于1.234時，膠筒在載荷作用下發生不穩定約束變形。高徑比在1.234～1.405范圍內時，膠筒達到約束穩定變形的載荷值隨高徑比的增大而增高；高徑比在1.405～1.982范圍內時，膠筒過渡到穩定變形的載荷值穩定在2.07 MPa；當高徑比大于1.982后，膠筒實現穩定約束變形所需要的載荷值略有升高，但在高徑比大于2.072，達到穩定變形所需的載荷值重新保持在2.08 MPa后不再變化。

(4)當膠筒材料取HNBR、NBR、FKM和PU不同材料時，高徑比變化時材料差異對自由變形階段所需要的使膠筒與套管接觸的最小載荷和約束變形階段從不穩定變形過渡到穩定變形所需要的載荷值的變化趨勢的影響不明顯，但對自由變形階段使膠筒與套管接觸的最小載荷值、約束變形階段從不穩定變形過渡到穩定變形所需要的載荷值有顯著影響。4種材料中，PU材料在自由變形階段所需要的使膠筒與套管接觸的最小載荷和約束變形階段從不穩定變形到穩定變形所需要的載荷值普遍最高，然后依次是HNBR、NBR和FKM，且HNBR與NBR在高徑比小于1.234，FKM與PU在高徑比小于1.225時，不會出現膠筒不穩定變形的情況。