套管式相變蓄熱器內管排列方式和壁溫的影響

郭夢雪

(山東建筑大學熱能工程學院，山東濟南250101)

1 概述

相變材料因其蓄熱和放熱時雖然溫度波動小但是吸收和釋放的潛熱特別大而且具有過程容易控制等優點受到了普遍的關注[1]。根據相變材料的不同相態和類型，相變過程可分為4種類型：固-固相變、固-液相變、固-氣相變和液-氣相變。由于固-氣相變和液-氣相變會在相變過程中產生氣體，相變過程不容易控制，并且所需蓄熱器體積龐大，因此，在工業中很少使用。相變材料的固-液單位質量蓄熱量很大，安全可靠，易于控制，但缺點是熱導率相對較小，會影響吸放熱過程中的傳熱速率，因此，必須采取有效的技術措施來提高其性能[2]。

由于相變材料在能源儲存方面有極大的潛力，在節能以及溫度控制領域有很好的前景，因此，如何將相變蓄熱技術利用到極致已經成為國內外學者的研究熱點之一。例如，文獻[3]通過溫度熱阻迭代法建立了同心套管相變蓄熱器的傳熱模型，對相變材料蓄熱器的結構進行了優化分析。文獻[4]利用實驗與數值計算相結合的方法模擬了殼管式換熱器內相變材料熔融和凝固過程，流體入口溫度對相變材料的熔化和凝固過程有很大的影響。文獻[5]研究了相變材料相變過程中的動態參數，將同一蓄熱器分別填充水和相變材料進行比較，得出填充相變材料的換熱器蓄熱效果更好的結論。文獻[6]通過CFD模擬了兩種不同結構的蓄熱器的蓄熱能力和傳熱方式，結果表明，合理增加換熱器內管的數量可以提高蓄熱器的蓄熱能力。文獻[7]以石蠟作為相變材料建立了圓外管相變實驗系統，得到了蓄熱、放熱過程中不同部位石蠟的相變規律，以及石蠟熔化時間。文獻[8]通過焓法建立了殼管蓄熱器中相變材料的吸熱和放熱過程的數學模型。通過數值模擬分析了石蠟的熔化和凝固過程。文獻[9]建立了一個熱管網路，由一個主熱管和同心熱管組成，對其進行數值模擬，并對熱管的幾何形狀進行了優化。文獻[10]利用數值模擬的方法研究了多排管式相變蓄熱器，得出相變材料使用膨脹石墨與石蠟混合物可提高蓄熱效率。文獻[11]研究了雙換熱管中相變材料的熔化和凝固過程，得到偏心率影響蓄放熱過程的結論。

商業軟件COMSOL Multiphysics涵蓋多種模塊，最大優點是可以解決多物理場耦合的問題，適合于多個專業。本文通過COMSOL Multiphysics軟件建立正方形、菱形1、菱形2三種不同的排列方式的換熱內管分布在填充了相變材料石蠟中的蓄熱器傳熱模型。并對模型進行了數值計算，分析了不同排列方式的換熱內管對相變蓄熱器的傳熱過程的影響，以及當換熱內管排列方式一定時內管壁溫對傳熱性能的影響。

2 模型的建立

2.1 物理模型

本文研究的相變蓄熱器為臥式套管式蓄熱器。蓄熱器的組成部分有3個：外管、4根相同的內管、相變材料石蠟。外管直徑較大，兩端封閉，長度為480 mm。4根相同內管直徑較小,兩端開放，長度為500 mm。外管套在4根內管外面。內管兩端連接傳熱流體。外管和內管之間的封閉空間封裝著石蠟。蓄熱器蓄熱時，熱流體從內管的一端流向另一端，石蠟受熱熔化，吸收熱量；蓄熱器放熱時，冷流體以相反的方向從內管中流過，石蠟受冷凝固，放出熱量。

外管和內管的壁厚均不到1 mm，在計算和測量時不計壁厚。管半徑均為管內壁半徑。本文是在內管半徑和外管半徑之比為1∶5的條件下，改變內管的排列方式。內管半徑r=10 mm，外管半徑R=50 mm。內管數量設置為4個是為了增強傳熱效果。文獻[12]指出，當內管管中心間距較大時(管中心間距=1.5倍內管直徑)時，熔化形狀沿界面豎直方向發展。因此，依次相鄰內管之間的中心間距均設為：d1=30 mm。

為了便于分析，減少計算量，對物理模型進行合理的簡化，在內管管長與半徑之比不是很大的情況下，可認為流體進出口溫度基本相同，即沿管長方向沒有熱量傳遞。這樣將三維裝置簡化為二維模型。設置外管中軸線為z軸，沿z軸方向可認為傳熱流體沒有熱量損失，液態石蠟不沿z軸流動。z軸上任一點為坐標原點O，在坐標原點O作垂直于z軸的xOy平面，得到xOy平面上的二維截面,即為研究對象。在此截面上x軸正向水平向右，y軸正向垂直向上。不同換熱內管排列方式的蓄熱器物理模型見圖1。

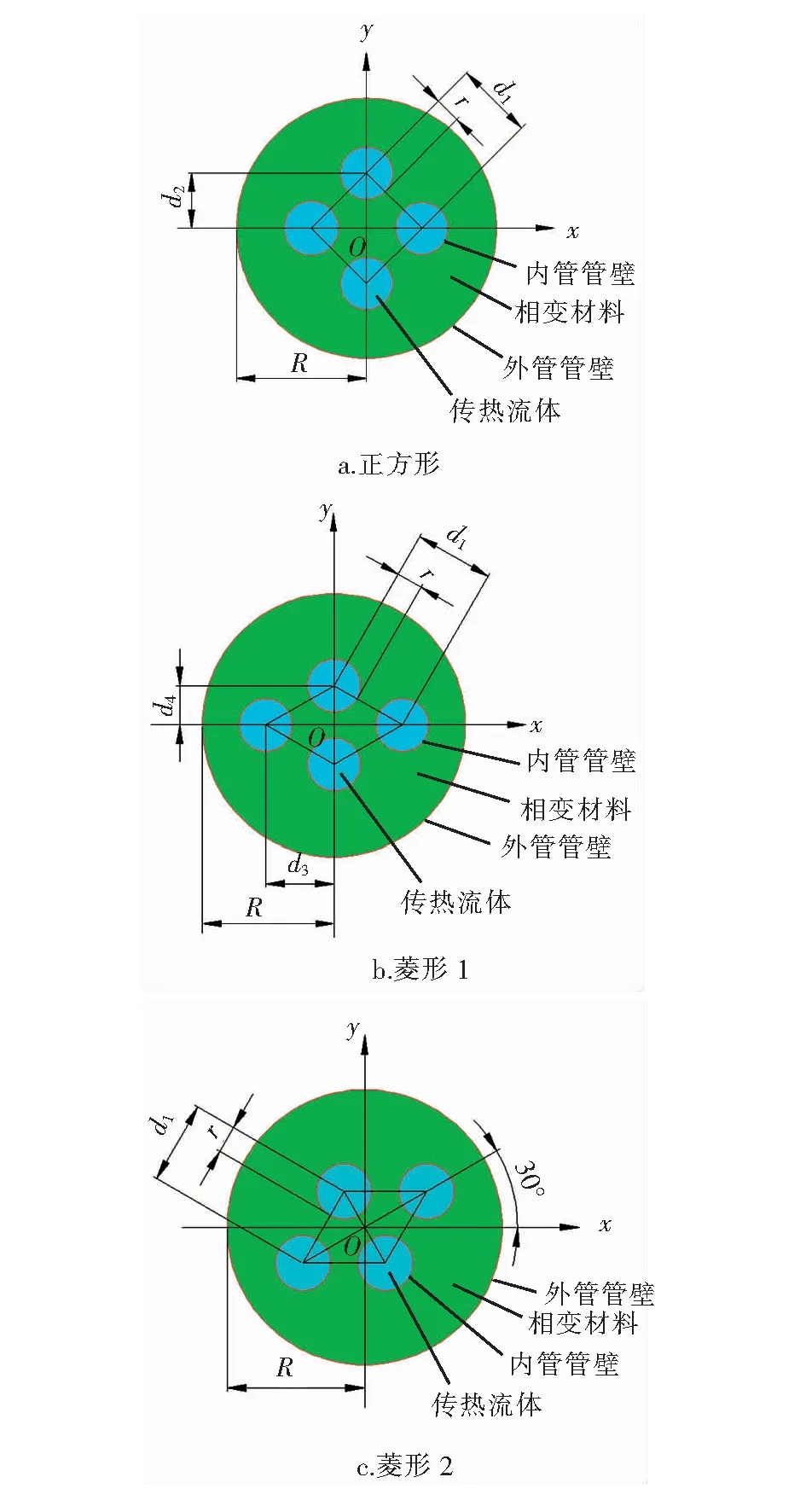
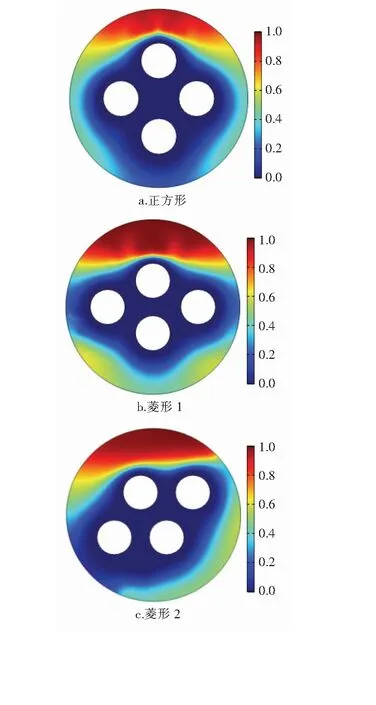
圖1 不同換熱內管排列方式的蓄熱器物理模型

為了探究內管不同排列方式對蓄熱器換熱的影響，分別建立正方形、菱形1、菱形2三種不同的內管排列方式，均勻分布在外管內部。石蠟在外管和內管之間熔化和凝固，液態石蠟受熱內管壁或冷內管壁的影響，會有密度的變化，受到重力和浮升力的作用，形成環狀自然對流，內管排列方式的改變或者角度的改變都會影響石蠟熔化和凝固的形態。4根內管的排列方式分別為：

a. 正方形排列：4根內管的圓心分別位于正方形4個頂點處，正方形的中心位于坐標原點O，頂點在x軸和y軸上。正方形的邊長為d1=30 mm。正方形中心到頂點的距離為d2=21.21 mm。

b.菱形1：4根內管圓心分布在菱形4個頂點處，菱形的中心位于坐標原點O，對稱軸長軸位于x軸，頂點距原點距離d3=25.98 mm。對稱軸短軸位于y軸，頂點距原點距離d4=15 mm。菱形的邊長為d1=30 mm。

c.菱形2：將菱形1以中心為圓心，逆時針旋轉30 °。

為了簡化計算，需要對計算模型進行一些設定和簡化：

① 石蠟的密度和相變溫度為常數。

② 石蠟的物性參數在固、液相中不隨溫度發生變化，處于熔融狀態時，參數隨溫度線性變化。

③ 液相為牛頓不可壓縮流體，并且符合Boussinesq假設。浮升力中的液相石蠟密度隨溫度線性變化。

④ 外管壁面與外界絕熱。

⑤ 內管和外管的壁厚為0，熱阻為0，忽略其對傳熱效果的影響。

2.2 數學模型

由于石蠟是在一個溫度區間內發生和完成相變的。因此，固相區和液相區之間會有一個未完全熔化和凝固的固液共存的區域，稱為糊狀區。該數學模型遵循三大守恒定律，即質量守恒、動量守恒和能量守恒。該模型的控制方程式如下[13](以下公式中的物性參數均為石蠟的物性參數)：

連續性方程：

(1)

式中ρ——密度，kg/m3

t——時間，s

u——x方向速度，m/s

x——x軸坐標，m

v——y方向速度，m/s

y——y軸坐標，m

動量方程：

(2)

(3)

(4)

(5)

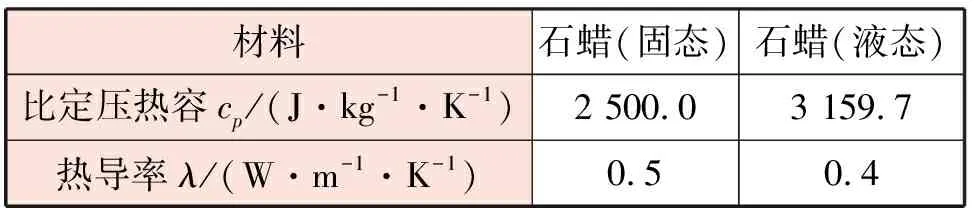
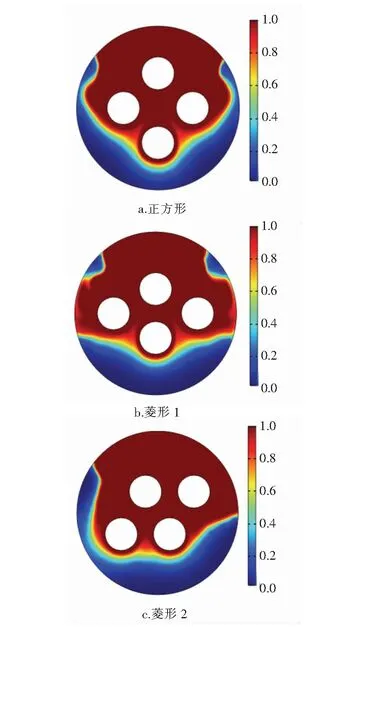
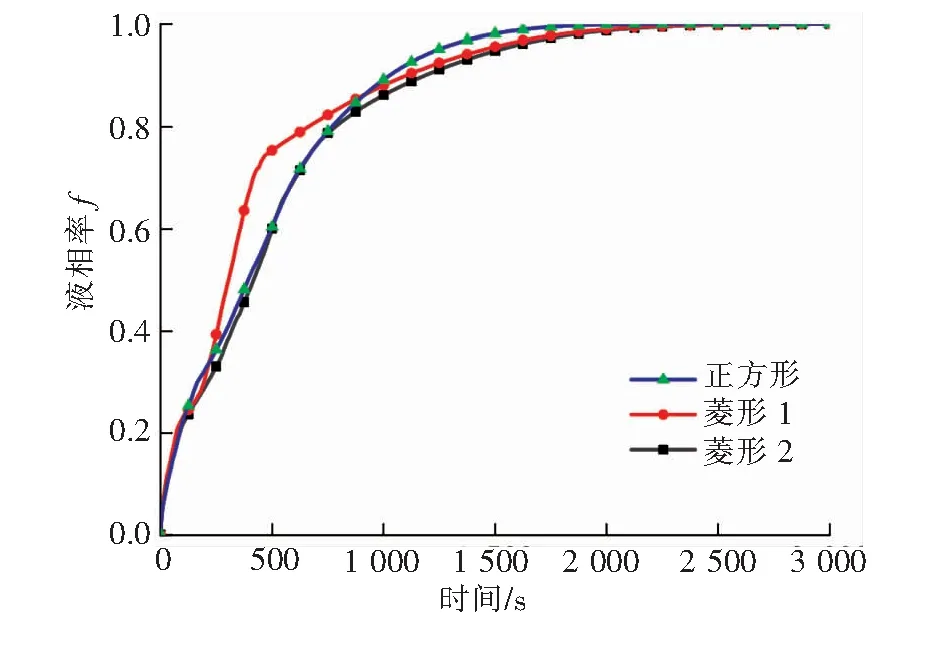
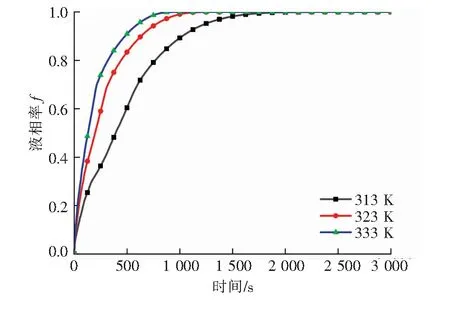
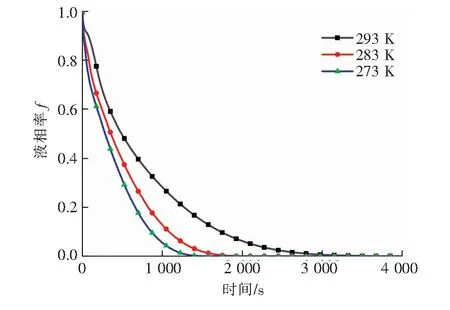
當T

f=0

(6)

當Ts≤T≤Tl時，

(7)

當T>Tl時，

f=1

(8)

式中μ——動力黏度，Pa·s

p——絕對壓力，Pa

Su——u方向動量方程源項

Sv——v方向動量方程源項

f——液相率

ε——系數，取10-3

Amush——糊狀區的連續數系數，取5×104

ρref——石蠟的基準密度，即石蠟的初始密度，kg/m3

g——重力加速度，m/s2

α——體積膨脹系數，K-1

T——任意時刻石蠟溫度，K

Tref——石蠟的基準溫度，即石蠟的初始溫度，K

Ts——相變初始溫度，即固相溫度，K

Tl——相變終止溫度，即液相溫度，K

石蠟熔化或者凝固過程中，會出現3個區域，完全為液態石蠟的液相區，完全為固態石蠟的固相區以及固液交界面處液態石蠟和固態石蠟相互摻混的糊狀區。糊狀區的產生是由于熔化溫度是一個范圍值，有熔化起始溫度和熔化終止溫度，因此固液交界面處會出現固液摻混現象。糊狀區到液相區會發生一個黏度急劇增大的現象，為了限制糊狀區速度的發展，添加一個大小合理的力Su和Sv。液相率f為液相和固相共存狀態下，液相體積與液、固相混合物總體積之比。為了防止公式(4)和(5)分母為0，建立了一個小于或等于0. 001的系數ε，本文ε取10-3。

能量方程：

(9)

(10)

h=hs+Δh

(11)

(12)

Δh=frq

(13)

式中h——任意時刻比焓，J/kg

λ——熱導率，W/(m·K)

cp——比定壓熱容，J/(kg·K)

Sh——能量方程源項

hs——顯熱比焓，J/kg

Δh——潛熱比焓，J/kg

href——石蠟基準比焓，即初始比焓，J/kg

rq——相變潛熱，J/kg

2.3 邊界條件以及初始條件

本文模擬了4種工況，分別為：

① 工況1：保持內管壁溫和石蠟初始溫度不變，當內管排列方式發生變化時，模擬石蠟熔化。

② 工況2：保持內管壁溫和石蠟初始溫度不變，當內管排列方式發生變化時，模擬石蠟凝固。

③ 工況3：保持內管排列方式和石蠟初始溫度不變，當內管壁溫變化時，模擬石蠟熔化。

④ 工況4：保持內管排列方式和石蠟初始溫度不變，當內管壁溫變化時，模擬石蠟凝固。

2.3.1 邊界條件

外管壁面絕熱，內外沒有熱量傳遞。忽略壁面厚度以及管壁熱阻對傳熱的影響，將內管壁面溫度設定為恒定的內管內傳熱流體的溫度。不同模擬工況下的內管壁溫見表1。液態石蠟的流動設為層流流動。石蠟在豎直方向施加重力作為原始驅動力。

表1 不同模擬工況下的內管壁溫

2.3.2 初始條件

蓄熱器內石蠟熱物性參數見表2。

表2 石蠟熱物性參數

不同模擬工況下的石蠟初始溫度見表3。

表3 不同模擬工況下的石蠟初始溫度

石蠟相變的初始溫度Ts=295 K，相變的終止溫度Tl=311 K。石蠟的相變潛熱rq= 2×105J/kg，體積膨脹系數為α=10-3K-1，初始密度ρref=900 kg/m3。動力黏度μ=4.43×10-3Pa·s，初始內部絕對壓力為pref=1.01×105Pa。相變開始之前認為石蠟沒有相變，速度為0 m/s，熔化之前為純固體，凝固之前為純流體。

3 模型求解

利用COMSOL Multiphysics軟件對模型進行求解。通過耦合層流和固體傳熱兩個物理場，求解連續性方程、動量方程和能量方程。層流物理場里設置液態石蠟的初始值以及物性參數。為液態石蠟的流動添加浮升力和重力。固體傳熱物理場里設置固態石蠟的初始值和物性參數，設置邊界條件，添加相變材料項，將石蠟性質設置為相變材料。最后將求解器設置為瞬態求解器，得到結果。

4 結果與討論

4.1 不同內管排列方式對傳熱的影響

① 工況1

t=500 s時3種不同內管排列方式的石蠟熔化液相率分布見圖2。圖2中,色標右面的標值為石蠟的液相率(圖4與此同)。在該圖中，藍色區域是固相石蠟，紅色區域是液相石蠟，兩者之間的黃綠色區域是糊狀區。固液界面處于不規則形態，這是由于液相區域自然對流的影響。一般上方區域的石蠟先熔化，再熔化下部，因為液相石蠟受熱，密度減小，受到向上的浮升力，形成環狀自然對流。正方形排列由于距離外管上下左右距離合適又相等，因此熔化比較均勻，呈碗狀分布。菱形1排列上部兩側會有兩個區域的石蠟較難熔化，這是因為距離內管較遠。菱形2排列因為內管偏右排列，所以左上部會有一個區域較難熔化。

圖2 t=500 s時3種不同內管排列方式的石蠟熔化液相率分布

圖3為不同排列方式換熱內管石蠟熔化液相率曲線。開始階段，正方形排列熔化速率比菱形1慢。菱形1排列石蠟熔化速度最快，液相率也最大。是因為菱形1呈扁寬形狀，開始階段靠近外管兩側的區域熔化快。而后速度變慢是因為菱形1和菱形2距離外管壁下部較遠，容易造成死區。排列方式為正方形、菱形1、菱形2的蓄熱器的石蠟完全熔化(f=1)的時間分別為2 100 s、2 680 s、2 720 s。與正方形排列方式相比，菱形1和菱形2的蓄熱器的石蠟完全熔化時間分別增加了21.64%、22.79%。

圖3 不同排列方式換熱內管石蠟熔化液相率曲線

② 工況2

t=1 000 s時3種不同內管排列方式的石蠟凝固液相率分布見圖4。石蠟接觸到低溫的內管壁開始凝固，石蠟的下部先開始凝固，然后才是上部開始凝固。液態石蠟受冷，密度增大，形成環狀自然對流。正方形排列由于在外管內部分布均勻,因此凝固也會比較均勻。菱形1排列和菱形2排列由于內管分布距離和角度的差異,會分別使下部兩側和下部右側的石蠟較難凝固。

圖4 t=1 000 s時3種不同內管排列方式的石蠟凝固液相率分布

不同排列方式換熱內管石蠟凝固液相率曲線見圖5，3條曲線的下降趨勢基本相同，正方形排列斜率最陡，其他兩個相差不大。排列方式為正方形、菱形1、菱形2的蓄熱器的石蠟完全凝固(f=0)的時間分別為3 710 s、4 740 s、4 630 s。與正方形排列方式相比，菱形1和菱形2的蓄熱器的石蠟凝固時間分別增加了 27.76%、24.80%。

圖5 不同排列方式換熱內管石蠟凝固液相率曲線

4.2 不同換熱管壁溫對傳熱的影響

① 工況3

選取3種排列方式中傳熱效果最好的正方形排列，對其進行不同內壁面溫度下石蠟熔化過程的研究。內管以正方形排列時不同內管壁溫條件下石蠟熔化液相率曲線見圖6。由圖6可知，3條曲線在熔化初期幾乎呈線性穩定上升，后期斜率逐漸減小。內管壁溫越高，石蠟完全熔化所需時間越短，這是因為蓄熱器內部的主要傳熱方式為自然對流。不同內管壁溫時石蠟完全熔化的時間差別非常明顯，當壁溫從313 K上升到323 K、333 K時，熔化時間分別減少43.57%、57.14%。

圖6 內管以正方形排列時不同內管壁溫條件下石蠟熔化液相率曲線

② 工況4

內管以正方形排列時不同內管壁溫條件下石蠟凝固液相率曲線見圖7。3條曲線在整個凝固過程中幾乎呈平滑的下降趨勢，凝固曲線的斜率逐漸變小，曲線逐漸變得平緩。內管壁溫越低，完全凝固所需時間越短。當內管壁溫從293 K下降到283 K、273 K時，凝固時間分別減少47.57%、59.97%。在石蠟凝固初始階段，液態石蠟與低溫內管壁直接接觸，溫差大，凝固速度快。初始階段過后，導熱作為主要的傳熱方式，凝固速度降低，導致液相率下降的速度逐漸放緩。

圖7 內管以正方形排列時不同內管壁溫條件下石蠟凝固液相率曲線

5 結論

利用COMSOL Multiphysics軟件研究了蓄熱器的換熱內管數量相同時不同排列方式(正方形、菱形1、菱形2)以及不同內管壁溫對相變蓄熱器傳熱過程的影響。在外管壁為絕熱，內管壁溫恒定,熔化工況時石蠟的初始溫度為293 K，凝固工況時石蠟的初始溫度為313 K,石蠟初始時刻無相變的條件下,獲得如下結論：

① 蓄熱器內管的3種不同排列方式中，傳熱效果最好的是正方形排列，內管壁溫313 K時石蠟完全熔化和內管壁溫度293 K時石蠟完全凝固所需要的時間最短。

② 內管壁溫度從313 K增加到323 K、333 K時，正方形排列熔化時間分別降低了43.57%和57.14%。內管壁溫度從293 K下降到283K、273 K時，正方形排列凝固時間分別縮短了47.57%和59.97%。