射線追蹤方程與程函方程的初至旅行時層析對比

郭振波 孫鵬遠 李培明 任曉喬 錢忠平 唐博文

(東方地球物理公司物探技術研究中心，河北涿州 072751)

0 引言

對于油氣地震勘探，需建立較精確的近地表模型以消除地表起伏及近地表速度異常對反射信號的影響，特別是對于山地等復雜探區，近地表模型的精度直接決定了最終的成像效果[1-2]。由于初至旅行時的穩健性及旅行時層析的高效性，目前利用初至旅行時層析反演進行近地表建模是應用最廣泛的方法。近地表模型通常用于靜校正[3]、深度域建模[4]等處理流程。

經典的初至層析反演方法基于射線追蹤方程，在反演中需要顯式計算炮點到檢波點的旅行時及射線路徑[5]，本文將這類經典的初至層析反演方法稱為基于射線追蹤方程的初至層析反演方法。反演中通常采用兩種方式求取旅行時及射線路徑：①采用兩點射線追蹤[6]或類似方法同時求取旅行時及射線路徑；②采用波前追蹤類方法，如基于程函方程的有限差分類方法[7-8]、基于線性旅行時假設的線性旅行時插值方法[9]、基于圖理論的最短路徑方法[10]等，該類方法需在求解得到初至時間場的基礎上從檢波點開始反向追蹤得到射線路徑[9，11-12]。反演通常采用反向投影[13]、最小二乘奇異值分解(LSQR)[11]、同時迭代重構(SIRT)[14]等方法。基于射線追蹤方程的層析反演方法已在實際生產中廣泛應用，目前主要研究方向是如何與波形反演等精度較高的反演方法相結合[15-16]。

除了上述經典算法外，還存在一類層析反演算法，本文將其稱為基于程函方程的層析反演方法。該類方法僅需要計算初至時間場而不需要計算射線路徑，借助伴隨狀態方法[17]求取模型更新量。該類方法最早由Sei等[18]于1994年提出，近年來得益于波形反演的興起，伴隨狀態方法為地球物理學家所熟知，進而開展了廣泛的研究。Leung等[19]、Taillandier等[20]、謝春等[21]采用快速掃描方法進行初至旅行時層析； Huang等[22]利用該方法進行透射及反射旅行時層析； Benaichouche等[23]、李勇德等[24]討論了該類層析方法中預處理方法對層析的影響； Waheed等[25]將該類方法用于各向異性介質的初至旅行時層析。

雖然兩類方法已得到了廣泛研究，但目前還沒有從理論及數值測試上進行系統的對比分析。本文首先基于統一的反演框架從方法原理上對兩種方法進行了詳細的對比分析，并做了定性的評價；然后通過一個數值測試實例，對兩種方法的反演精度、計算效率、內存占用等情況進行了定量的對比分析。

1 方法原理及對比分析

1.1 層析反演基本理論

旅行時層析通過迭代反演尋找正演旅行時與觀測旅行時最優擬合的模型，若不考慮正則化項，L2模的目標函數可寫為

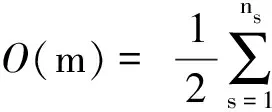
(1)

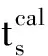
將目標函數在m0處展開且只保留至二階項，可整理為

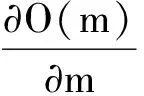
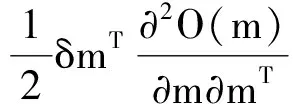
(2)

通常將目標函數相對于介質參數的一階導數稱為梯度，即

(3)

將目標函數相對于介質參數的二階導數稱為Hessian矩陣，即

(4)

由于求取目標函數最小，需要求取目標函數的駐點，即g=0的點。對式(2)求導并將其設為零，可得

H|m0δm=-g|m0

(5)

δm=-(H|m0)-1g|m0

(6)

式(6)為在當前模型m0下對應模型更新量的顯式表示。利用δm更新當前模型參數m0并將其作為下次迭代的初始模型，可實現非線性反演。當目標函數小于給定的閾值時，停止迭代，得到最終的反演模型。

由于Hessian矩陣的逆很難直接求取，通常通過迭代反演的方式求取式(5)所示的線性方程，此時反演方法通常稱為高斯—牛頓法。對于尺度較大的問題，Hessian矩陣H的求取非常耗時且存儲困難，通常需要對其進行近似處理。若將Hessian矩陣近似為一單位矩陣，則退化為最速梯度方法；若將Hessian矩陣近似為對角或帶限矩陣，則退化為預處理的最速梯度方法。

1.2 基于射線追蹤方程的初至層析反演

對基于射線追蹤方程的初至層析反演，需要求取每個炮檢對的射線路徑，在得到射線路徑之后，可將初至時間表示為

(7)

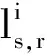
(8)

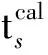
假設每次迭代的模型更新量不大，不足以引起射線路徑的劇烈變化，即?Ls(m)/?m=0。利用該假設，將式(8)代入式(1)，利用式(3)可求得一階梯度為

(9)

利用式(4)可求得二階Hessian矩陣為

(10)

若利用對角元素近似Hessian矩陣，并將其代入式(6)，通過整理可得到反向投影算法的基本公式

(11)

式中δts，r為第s炮的第r個檢波點處的初至旅行時殘差。

將式(9)和式(10)代入式(5)，整理可得

(12)

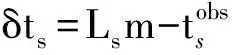
1.3 基于程函方程的初至層析反演

基于程函方程的初至層析反演方法直接采用程函方程而不是射線追蹤方法作為反演中的正演方法。各向同性介質中初至旅行時的傳播滿足程函方程，利用迎風有限差分進行離散之后的形式為

(Dxts)(Dxts)+(Dyts)(Dyts)+(Dzts)(Dzts)

=diag(m)m

(13)

滿足初始條件

ts(is)=0

(14)

式中：ts為第s炮對應的所有網格點上的初至時間；Dx、Dy、Dz分別為x、y、z方向的迎風差分矩陣；diag(m)為將慢度向量的元素放在對角位置形成的對角矩陣；is為第s炮震源網格序號。本文利用基于快速匹配方法的迎風差分方法[26]求解式(13)。

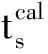
(15)

將式(15)代入式(1)，利用式(3)可求得一階梯度為

(16)

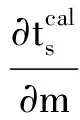
diag(Dzts)Dz]-1diag(m)

(17)

將式(17)代入式(16),可得一階梯度為

(18)

由于很難直接求解上式中矩陣的逆，對于單炮梯度可通過有限差分方法求解如下方程得到

(19)

式(19)是Taillandier等[20]的連續形式偏微分方程式(13)的離散形式。本文對式(19)采用迎風差分方法求解。

利用式(4)可求取Hessian矩陣為

(20)

由于式(17)中存在矩陣的逆，通常無法直接求解。將式(20)代入式(5)，通過整理可獲取其等價的形式為

(21)

若在每次非線性迭代內部迭代求解式(21)即為高斯—牛頓法。若只保留Hessian矩陣對角元素，則為預處理的最速下降方法。

1.4 對比分析

上文基于相同的目標函數，在統一的反演框架下分別推導了基于射線追蹤方程與程函方程初至旅行時層析迭代反演的基礎公式。詳細對比兩者的理論推導過程，兩類方法具有如下共性。

(1)具有相同的理論基礎。理論初至旅行時的計算均采用基于高頻近似的射線理論進行；初至旅行時反演采用統一的目標函數，且均可在統一的反演框架下推導迭代反演的基本公式。

(2)具體反演算法之間具有對應性。基于射線追蹤方程方法中的反向投影算法與基于程函方程方法的預處理最速下降方法是對應的；基于射線追蹤方程方法中的LSQR、SIRT等與基于程函方程方法中的高斯—牛頓算法是對應的。對應方法之間可產生相近的效果。

由于兩者在理論上的相似性，兩者具有相似的分辨率以及處理復雜問題的能力，如兩者均無法解決速度反轉等復雜探區的問題。

兩種方法在理論上具有如下的主要區別。

(1)二者所基于的正演算子不同。前者基于射線追蹤方程，即旅行時為沿射線路徑對慢度的積分；后者基于程函方程，即利用有限差分等數值解法通過求解程函方程得到檢波點處的初至時間。

(2)二者求取或構造目標函數相對于介質參數一階梯度及二階Hessian矩陣的方式不同。對于前者，可利用不同網格內射線段長度顯式地構建一階及二階導數所對應的矩陣(式(9)、式(10))，直觀且物理意義明確；對于后者，只能通過隱式數值求解偏微分方程(式(19))得到單炮所對應的梯度，對于Hessian矩陣則很難顯式地進行構建，只能通過間接的方式考慮Hessian矩陣的影響，物理意義相對不明確。

基于理論上的異同，結合具體實現細節(如圖1所示兩種方法的反演流程對比)，在實際應用中，基于射線追蹤方程的初至層析反演方法具有如下優勢。

(1)反演過程中針對性處理更為靈活。可利用已知的射線路徑計算射線角度、射線密度等信息，可利用這些信息在反演的過程中進行針對性處理。

(2)豐富的質控方法。將射線路徑、射線角度、射線密度等利用圖形化的方式進行顯示，可對最終的反演方法進行有效的質控，如可檢查射線是否到達模型邊界、根據射線密度判斷不同部位反演模型的可靠程度等。

基于程函方程的初至層析反演方法具有如下優勢。

(1)避免了射線路徑的計算以及由于射線路徑計算引入的誤差。由于初至旅行時只考慮最小時間且由于地表起伏可能引起的散射，實際處理中很少直接進行顯式的射線追蹤，而是在利用程函方程計算得到初至時間場的基礎上通過從檢波點處反向追蹤得到射線路徑。不管是采用梯度方法[7]還是線性旅行插值方法[9]，均基于局部近似，求取射線路徑存在一定誤差，特別是在地表起伏等復雜近地表條件下。若采用基于射線追蹤方程的層析反演，需顯式進行射線路徑的求取，在增加計算量的同時也在反演過程中也引入了部分誤差。由于不需要進行射線路徑的求取，因此基于程函方程的層析反演有效地避免了這個問題。

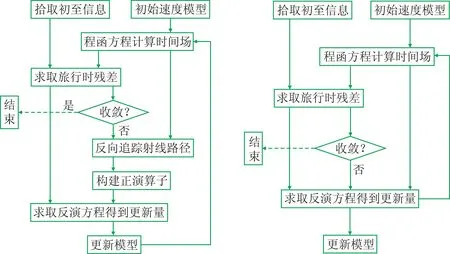
圖1 兩種層析反演方法反演流程對比

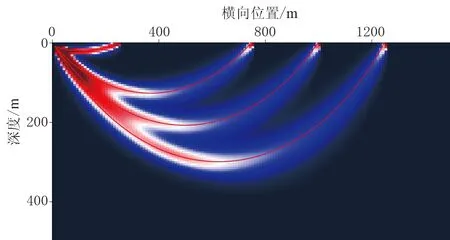
圖2 兩種反演方法核函數對比背景圖片為基于程函方程層析反演的核函數； 紅色

(2)計算效率及占用內存大小主要受模型大小的影響，與檢波點個數基本無關。在基于程函方程層析反演內部，主要利用有限差分求解式(13)、式(19)和式(21)，這些方程的計算效率及所需內存的大小僅與所用模型的大小有關，與檢波點的個數無關。

(3)如圖2所示，基于程函方程的層析反演方法核函數具有一定的寬度，在復雜區域反演效果略好。核函數代表空間任一位置一個散射點對走時變化的影響[27-28]，決定了梯度的形態。主要受差分算子的影響，基于程函方程的層析反演其核函數具有一定的寬度，類似于有限頻效應，在復雜區域理論上具有更好的反演效果。

2 數值對比分析

為了對比兩種方法在反演精度、計算效率、內存占用等方面的差異，選用Amoco靜校正基準測試模型(圖3)進行數值測試。該模型包含了大部分常見的近地表地質構造，如高速層出露、局部高速、低速異常體、淺層低速層、近地表復雜構造及極淺層低速體等，可進行較全面的對比分析。由于常規近地表建模通常的反演深度大約在1km左右，圖3所示模型是對原有模型在深度方向進行壓縮之后的結果，在保留原有模型復雜性的同時使其深度與常規近地表問題一致。

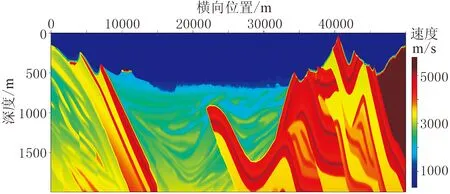
圖3 Amoco靜校正基準測試模型

2.1 反演精度對比

兩種反演方法內部的正演算子均通過數值求解程函方程實現，具體采用基于快速匹配追蹤的迎風差分算法[26]。對于基于射線追蹤方程的層析反演，在通過求解程函方程獲取時間場之后由檢波點位置開始沿初至時間場的負梯度方向追蹤射線路徑，最后計算每條射線所經過網格內射線段的長度來構建式(7)中對應的正演算子[13]。基于程函方程的層析反演采用預處理的最速梯度方法，預處理算子采用與Benaichouche等[23]、李勇德等[24]相同的形式，式(19)對應的方程采用迎風有限差分方法進行求解；基于射線追蹤方程的層析反演方法采用與最速梯度法對應的反向投影算法。除以上差別外，兩種反演方法均采用相同的處理方式，數值試驗時也選用相同的參數。

以25m為間隔在地表均勻布置共1998炮，每炮最大炮檢距為7500m，檢波點間距為20m。采用數值正演方法為層析反演生成合成數據。選用圖4所示線性遞增模型為初始模型，地表速度為4500m/s，速度隨深度變化梯度為0.5，在模型底部速度約為5500 m/s。圖5為基于射線追蹤方程的層析反演結果，圖6為基于程函方程的層析反演結果。對比圖5與圖6可知，從整體形態上來說，兩種反演結果基本一致，高速層出露、局部高速、低速異常體、淺層低速層、極淺層低速體等近地表地質構造均得到較好的反演。由于射線層析分辨率的限制，模型右側復雜構造區域均未取得理想的效果。從反演細節上來說，由于基于程函方程的層析反演其核函數是帶限的，即具有類似有限頻的特性，反演結果更加穩定，特別是在復雜構造區域，如圖5黑色箭頭所示區域，基于射線追蹤方程的層析反演結果存在局部的高速異常，但在基于程函方程的層析反演結果中不存在這類高速異常。從反演精度上來說，兩類方法具有相似的反演精度，在局部細節上基于程函方程的層析反演方法略優。由圖7的兩種方法殘差曲線對比可知，兩者具有相似的收斂效率。

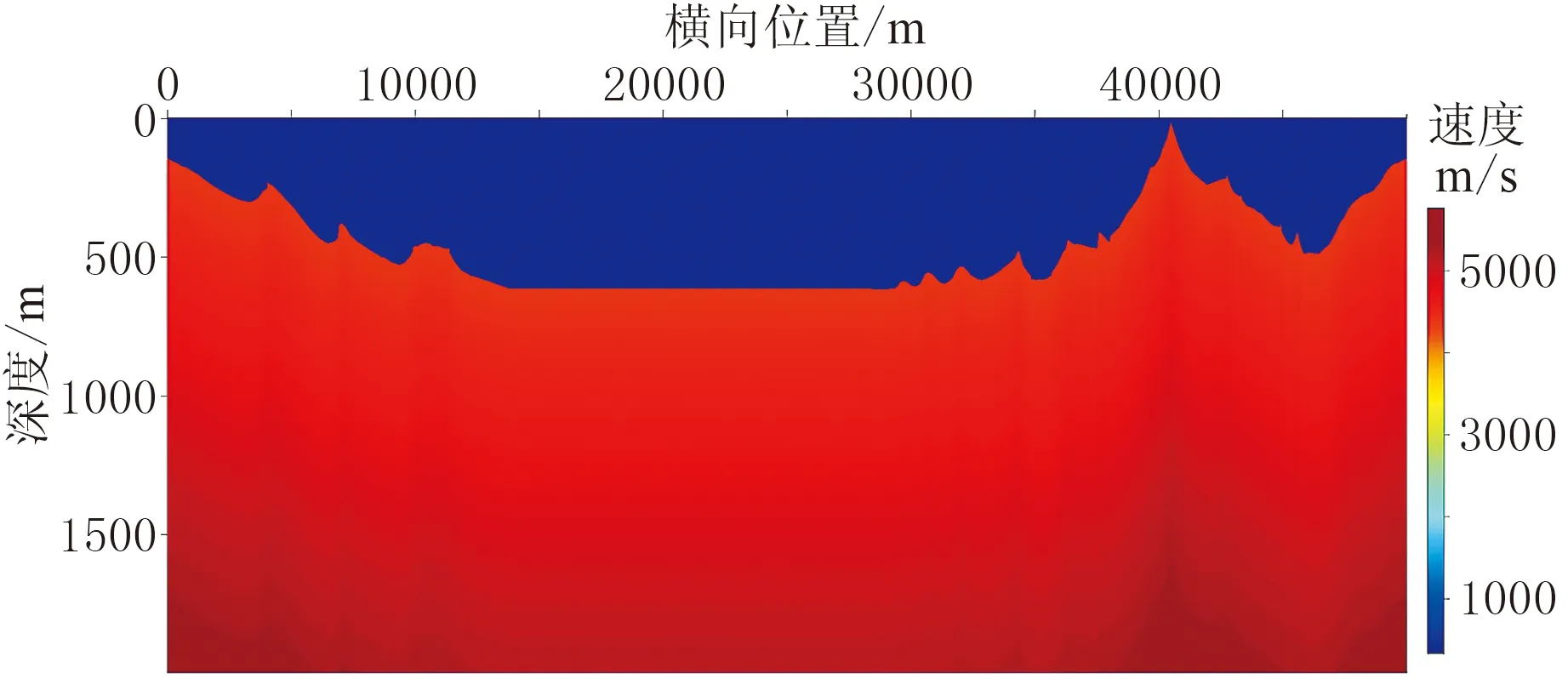
圖4 初始模型

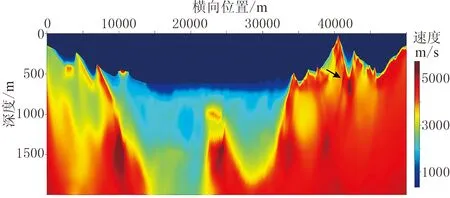
圖5 基于射線追蹤方程的層析反演結果

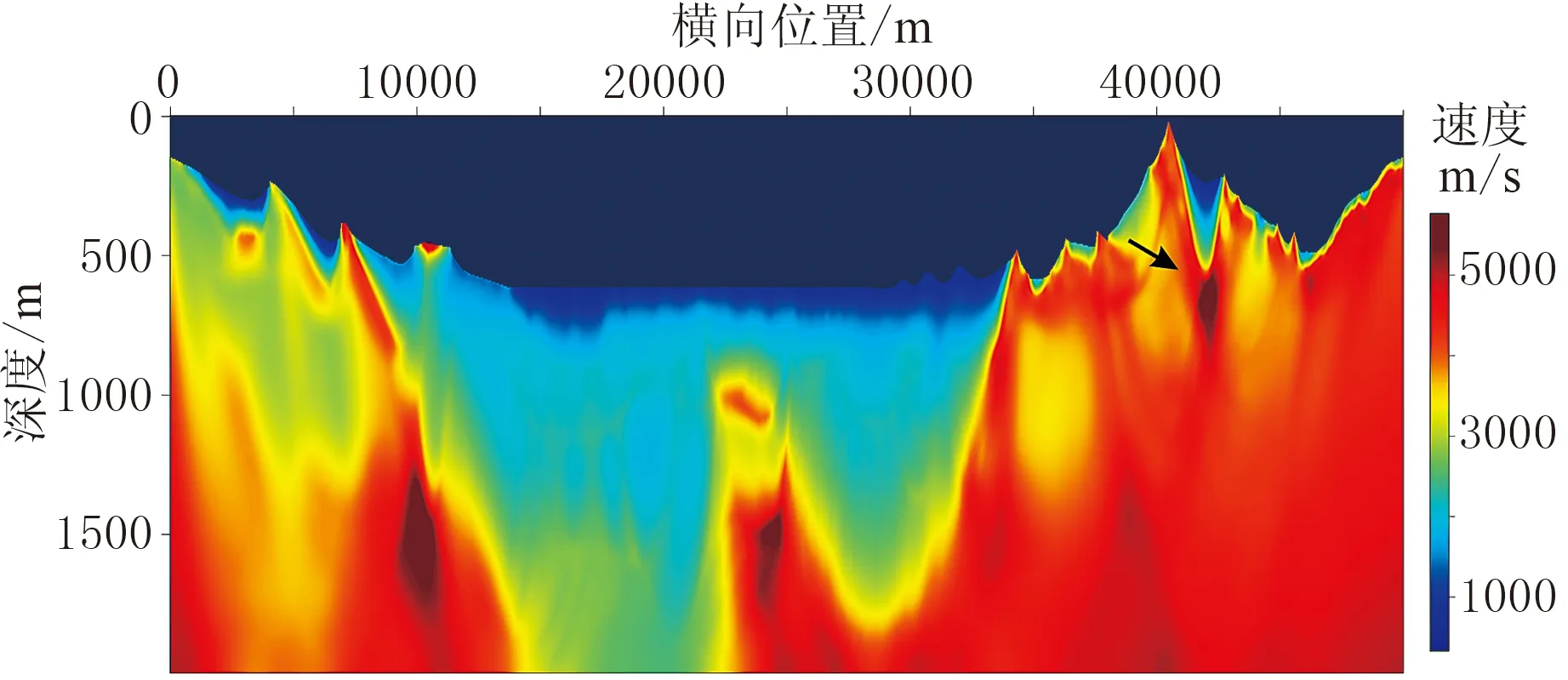
圖6 基于程函方程的層析反演結果

圖8為基于射線追蹤方程層析反演最后一次迭代的射線密度，利用射線密度可分析不同區域速度反演的可靠性。由于基于程函方程的層析反演沒有射線密度的概念，因此缺少類似的質控圖件。

2.2 內存占用及計算效率對比

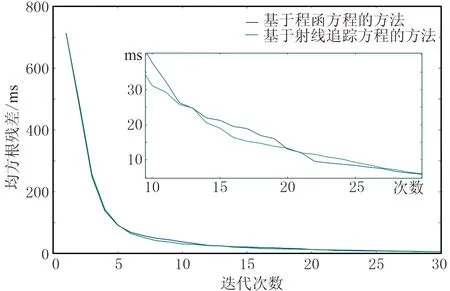
圖7 兩種方法反演殘差曲線對比

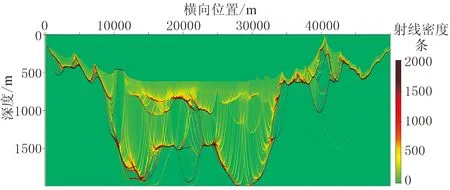
圖8 基于射線追蹤方程層析反演最后迭代的射線密度

為了在內存占用、計算效率等方面對兩種方法進行更全面的對比，設計了四種不同的觀測系統進行測試。由前面的理論分析可發現，基于射線追蹤方程層析反演的一個主要特點是其內存占用、計算效率等均是與檢波點個數相關的。基于這個主要差別，在固定總炮數、最大炮檢距的基礎上通過設置不同的檢波點間距(5、10、20、40m)模擬不同的觀測系統。測試環境為Linux集群，操作系統為企業版Red Hat 6.4，CPU為Intel(R) Xeon(R) CPU E5-2670(2.60GHz)，編譯器為Intel icpc。程序源代碼采用C++編寫，內部采用MPI并行處理。數值測試共用7個節點，每個節點有30個線程，每次層析反演迭代30次。

在不同觀測系統下內存占用(單進程對應內存占用)及運行時間對比如圖9所示，可以看出：①基于程函方程的層析反演內存占用及計算時間與檢波點個數無關，只與當前模型的大小有關；②基于射線追蹤方程的層析反演占用內存及計算時間均是檢波點個數的函數，檢波點個數越多，占用內存越大、計算時間越長；③當檢波點較密時，如寬方位、高密度等觀測數據，基于程函方程的層析反演方法在內存占用、計算效率等具有較大優勢；當檢波點稀疏時，基于射線追蹤方程的層析反演方法具有更大的優勢。

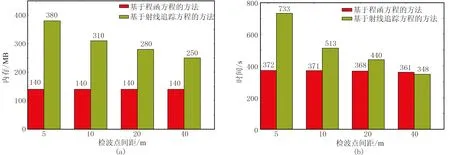
圖9 兩種方法在不同檢波點間距下內存占用(a)和運行時間(b)對比

3 結論

本文在統一的反演框架下推導了兩種層析方法的基本公式，在理論上對兩種方法的主要差別進行了定性的分析；通過理論數值測試，對兩種方法在反演精度、計算效率等方面進行了定量的分析。基于以上的分析，可以得出如下結論：

(1)兩種方法在理論上具有對應性，可在統一的反演框架下導出，且不同迭代反演方法之間均具有對應關系，主要的差別是由于反演中正演算子的不同引起；

(2)當基于射線追蹤方程的方法采用反向投影反演方法、基于程函方程的方法采用與之對應的最速梯度方法反演方法時，兩者具有相近的反演精度，基于程函方程的反演方法核函數具有類似有限頻的特性，在復雜構造中的反演更加穩定；

(3)計算效率及內存占用是兩者的主要差別。對于基于射線追蹤方程的層析反演方法，計算效率等依賴于檢波點個數，在檢波點特別稀疏時具有優勢；對于基于程函方程的層析反演方法，其主要依賴于模型大小，在檢波點間距較小時具有優勢；

(4)基于射線追蹤方程的層析反演方法具有射線密度等質控手段，是一個主要的優勢。

鑒于目前寬方位、高密度數據的大量采集，建議在實際中以應用基于程函方程的層析反演方法為主；在層析反演過程中選用部分炮進行射線追蹤以指導、控制反演過程并生成射線密度等質控圖件，從而充分利用不同方法之間的優勢。