基于巖相約束的Xu-White模型線性化近似與反演

凌東明 杜啟振 田 軍 王貴重 成 鎖 王繼勛

(①中國石油大學(華東)地球科學與技術學院，山東青島 266580； ②東方地球物理公司研究院庫爾勒分院，新疆庫爾勒 841001；③東方地球物理公司研究院，河北涿州 072751； ④中國石油塔里木油田公司勘探開發研究院，新疆庫爾勒 841000)

0 引言

巖石物理模型是儲層地質特性與地球物理特性之間的橋梁，用于建立儲層物性與彈性參數之間的關系[1]。巖石物理模型分為兩類：一是基于波動力學推導得到的理論模型及相應的近似模型，如K-T、Xu-White模型等[2-4]；二是利用實驗數據擬合得到的經驗模型，如Wyllie時間平均方程等[5]。理論模型的物理意義明確、理論依據充足，能夠更好地反映彈性參數與物性之間的關系。

儲層物性反演需要以巖石物理模型為基礎，由地球物理彈性參數預測儲層物性參數[6-10]。但由于理論模型的非線性特征較強，導致大多數物性反演方法利用復雜的非線性優化算法迭代求解，如共軛梯度法、馬氏鏈蒙特卡洛法、模擬退火法等[11-16]，此類算法多解性強且計算量巨大。針對巖石物理模型的非線性問題， Grana[17]采用一階泰勒級數展開法線性化近似巖石物理模型，并通過正演與反演方法分析經驗模型、顆粒介質模型和等效介質模型的近似結果，取得了一定效果；印興耀等[18]和Tian等[19]采用泰勒級數展開法線性化近似Xu-White模型，并通過縱、橫波速度正演驗證結果的有效性。前人研究成果表明，基于泰勒級數展開法線性化近似巖石物理模型具有一定的可行性，在已知點附近的精度較高，但在距已知點較遠處，難以保證精度。因而該方法適用于巖相單一、物性較均勻的地層，對于巖相復雜多樣、非均質性較強的地層則不適用。

在前人研究基礎上，本文提出基于巖相約束的Xu-White模型線性化近似方法，使之適用于非均質性較強的砂泥巖地層，并以疊前彈性反演成果為基礎，實現儲層物性線性化反演。該方法在模型試算及實際測試中，均表現出較好的應用效果。

1 Xu-White模型線性化近似方法與改進

1.1 Xu-White模型非線性原因分析

1995年，Xu等[3]在K-T模型的基礎上，應用微分等效介質理論推導出新公式計算砂泥巖地層的縱、橫波速度等彈性參數，該公式被命名為Xu-White模型。該模型是基于砂巖與泥巖的孔隙扁率具有顯著差異這一基本條件得到的，目前普遍應用于砂泥巖地層中。其計算可分為四個部分[3-4]。

(1)將孔隙空間區分為泥巖柔性孔隙與砂巖剛性孔隙兩部分，應用K-T模型計算干巖石體積模量與剪切模量

[ScTiijj(αc)+(1-Sc)Tiijj(αs)]

(1)

μdry-μma

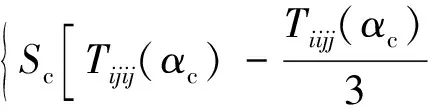
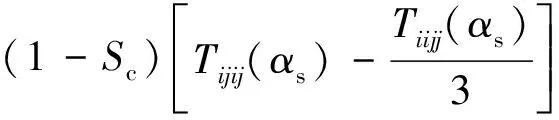
(2)

式(1)和式(2)中：Kdry、Kma和Ki分別為干巖石、巖石骨架和孔隙填充物的體積模量;μdry、μma和μi為相應的剪切模量；Sc為巖石骨架中的泥巖含量；αs為砂巖剛性孔隙扁率,αc為泥巖柔性孔隙扁率；Tiijj、Tijij是從張量函數Tijkl推導而來[20]，與Ki、μi、αs、αc和飽和巖石的泊松比等參數有關。

(2)應用微分等效介質理論，令φ為巖石總孔隙度，對式(1)、式(2)做進一步推導，得到

(1-Sc)Tiijj(αs)]

(3)

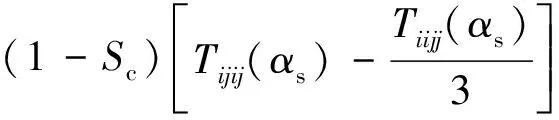
(4)

式(3)和式(4)為耦合非線性微分方程，求解過程非常復雜。但對于干巖石模量計算,Ki、μi取值為零，且泊松比可近似為常數。因此，可通過式(3)、式(4)得到干巖石模量簡化計算式

Kdry=Kma(1-φ)p

(5)

μdry=μma(1-φ)q

(6)

其中

(7)

(8)

(3)在求得干巖石模量基礎上，利用Gassmann方程計算飽和流體巖石體積模量與剪切模量。取Kf為孔隙流體的體積模量，可采用Reuss平均方程獲得

(9)

式中：Sw為飽和流體巖石孔隙中的含水飽和度；Kw和Khc分別為孔隙中地層水、碳氫混合物的體積模量。飽和流體巖石體積模量(Ksat)與剪切模量(μsat)通過

(10)

μsat=μdry

(11)

計算得到。取ρ為飽和流體巖石的等效密度，則

ρ=φ[ρwSw+ρhc(1-Sw)]+

(1-φ)[ρs(1-Sc)+ρcSc]

(12)

式中：ρw和ρhc分別為孔隙中地層水、碳氫混合物的密度；ρs和ρc分別為巖石骨架中砂巖顆粒和泥巖顆粒密度。

(4)結合式(10)～式(12)求取飽和流體巖石縱、橫波速度

(13)

(14)

在上述計算過程中，式(5)和式(6)中分別出現了指數系數p和q的形式，式(13)和式(14)中出現了平方根的形式，這四式是導致Xu-White模型非線性特征的主要原因,p和q與數值2之間的大小關系是決定巖石物理模型非線性強弱的關鍵因素。

p、q與巖石礦物模量、孔隙填充物體積模量、砂巖孔隙扁率、泥巖孔隙扁率及泥質含量相關。其中前四項為固定值，可通過巖石物理建模得到，泥質含量具空變特征，導致空間不同位置處的模型非線性特征不同。為研究p、q與泥質含量的關系，設定其他參數固定不變，泥質含量按照20%的間隔在0～100%范圍變化。考慮不同地質條件的影響，構建泥巖與砂巖孔隙扁率比參數(αc/αs)[4]，建立指數系數與孔隙扁率比關系圖(圖1)。

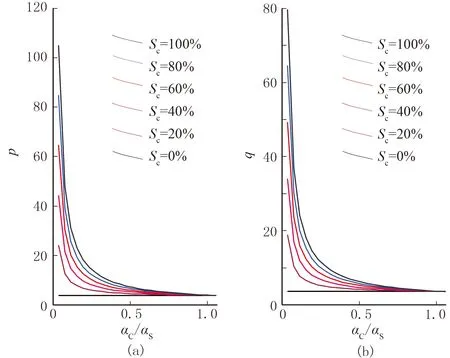
圖1 不同泥質含量的指數系數—孔隙扁率比關系圖

一般情況下，孔隙扁率比參數值遠小于1,p、q隨泥質含量增大急劇增大。圖1的不同泥質含量的模型曲線中，泥質含量從0至100%的線性變化分別對應p的最大值為2.7、22.4、43.1、63.8、84.5、105.2，對應q的最大值為2.8、17.4、33.1、48.6、64.2、79.8。可以看出，當泥質含量為0時,p、q略大于2，巖石物理模型為近線性特征；隨著泥質含量增加,p、q急劇增大，導致巖石物理模型為強非線性特征[4,21-23]。

1.2 Xu-White模型線性化近似方法

當前的巖石物理模型線性化近似方法采用泰勒級數展開、去除高階項之后得到一階近似結果。將該方法應用于Xu-White模型，對于由n個樣點組成的計算道，可將Xu-White模型正演過程寫成

d=f(m)+e

(15)

其中

(16)

式(15)和式(16)中：d為VP、VS和ρ組成的3n×1階矩陣；m為φ、Sc和SW組成的3n×1階矩陣；f為Xu-White模型函數；e為誤差向量。

基于該非線性模型進行反演，需應用復雜的迭代優化算法，此類算法多解性強，且計算量巨大。為此，對式(15)中的Xu-White模型函數f采用泰勒級數展開，保留一階項，得到線性近似式

d?f(m0)+Jm0(m-m0)+e

(17)

其中

(18)

式(17)中Jm0為模型函數f在已知點m0處的雅可比矩陣，可直接調用數學函數進行數值求解。反演過程中，將m0設置為屬性均值，可由測井數據統計得到。為研究Xu-White模型線性近似效果，選擇塔里木盆地哈得遜油田的W1井進行分析，該井包含實測縱波速度、橫波速度與密度曲線，通過計算得到孔隙度、泥質含量與含水飽和度曲線如圖2所示。

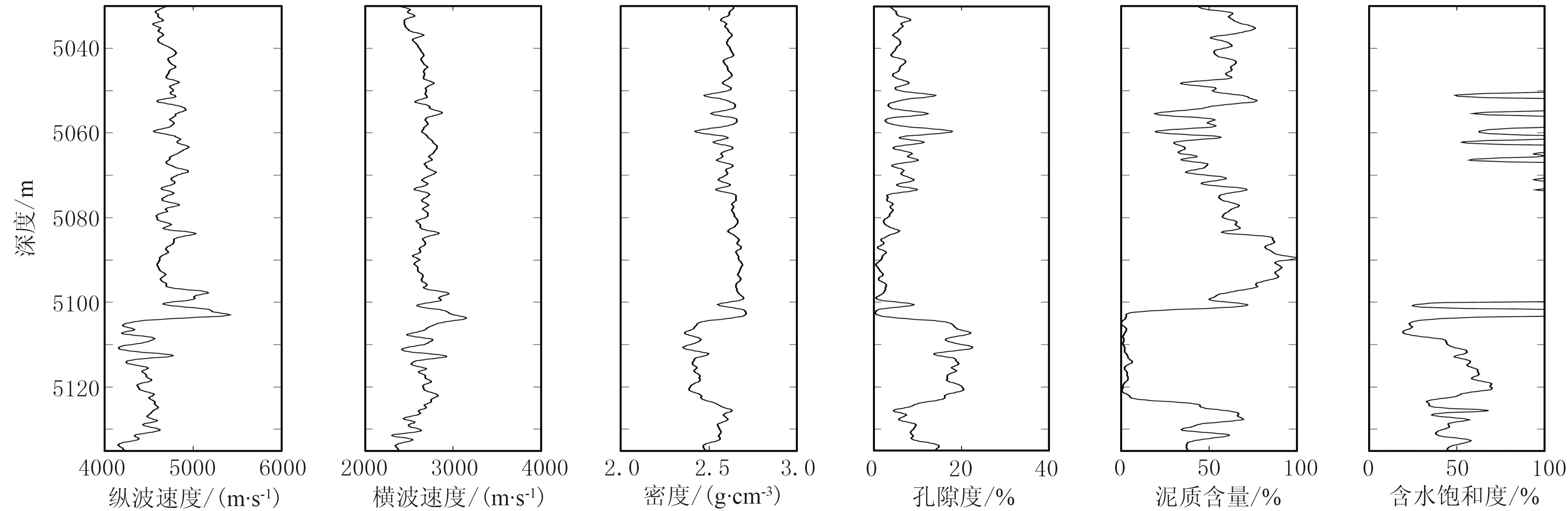
圖2 W1井實測彈性曲線與計算物性曲線

通過測井資料統計與實驗數據分析結果，給定各礦物組分和流體的巖石物理基本參數(表1)，并基于Xu-White模型開展巖石物理建模。由巖心薄片掃描電鏡結果獲得砂巖、泥巖孔隙扁率的初始參考值[24-25]。通過調整孔隙扁率，使計算縱、橫波速度與實測縱、橫波速度達到最佳擬合[6]，最終確定適用于本區的砂巖、泥巖孔隙扁率分別為0.172、0.027。

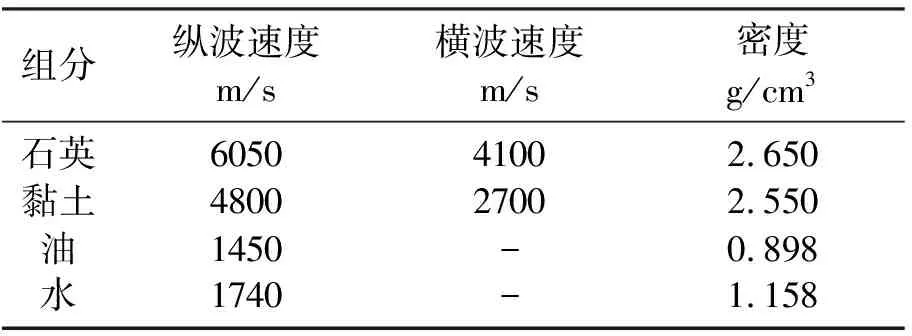
表1 巖石物理基本參數

以巖石物理建模參數為基礎，利用Xu-White模型的線性化近似(式(17))，分別開展模型及實測曲線的正演分析。模型分析中有3組18個正演模型，第一組包含6個正演模型，反映不同泥質含量、相同飽和度條件下縱、橫波速度隨孔隙度變化規律； 第二組反映不同孔隙度、相同飽和度條件下縱、橫波速度隨泥質含量變化規律； 第三組反映不同孔隙度、相同泥質含量條件下縱、橫波速度隨含水飽和度變化規律。

圖3a和圖3b為第一組正演模型，反映縱、橫波速度隨孔隙度變化規律，由圖可見，在泥質含量較小的條件下，Xu-White模型與其線性近似后的正演結果基本吻合。但隨泥質含量增加，在孔隙度低值段與高值段，差異性逐漸明顯。說明泥質含量越大，模型非線性特征越強，采用泰勒級數一階近似的正演結果與Xu-White模型出現較大偏差。

圖3c和圖3d為第二組正演模型，除孔隙度為零時表現為近線性特征，其他模型的非線性特征基本一致，說明孔隙度變化對模型非線性特征的影響較小。

圖3e和圖3f為第三組正演模型，趨勢一致且呈線性變化，說明含水飽和度基本不影響模型非線性特征。

綜上所述，泥質含量是影響Xu-White模型非線性特征的主要因素，泥質含量越大時，模型非線性特征越強(與圖1的分析結論完全吻合)；具有強非線性特征的巖石物理模型不能直接開展線性化近似，需要改進方法、提高精度。因此，利用反映泥質含量的自然伽馬曲線劃分巖相，針對不同巖相分別采用不同的孔隙度、泥質含量及飽和度均值進行泰勒級數一階近似，可改善儲層線性近似效果。

1.3 巖相約束的Xu-White模型線性化近似方法

利用反映泥質含量的自然伽馬曲線劃分巖相并作為約束條件，形成多個具有相似非線性特征的研究層段，實現強、弱非線性層段分離。巖相模型的建立可概括為兩個步驟：第一步，對測井曲線進行標準化處理，利用自然伽馬曲線確定泥巖基線，進而劃分出砂巖相與泥巖相；第二步，以地震層位為格架、地震波形為約束，利用單井巖相曲線進行井間插值(本文采用反距離加權插值算法)得到巖相模型體。巖相模型精度主要取決于地震格架的合理性、地震波形的保真度與參與曲線內插井的個數。

在不同的巖相內，由實際數據統計得到孔隙度參數的上、下限，用于確定研究范圍、找準均值點m0的位置，可有效改善線性化近似效果。在砂泥巖條件下，可假設巖石孔隙在不同組分中分布均勻，巖石總孔隙由砂巖基質孔隙和泥巖孔隙兩部分組成，即

φ=(1-Sc)φs+Scφc

(19)

式中φs、φc分別為砂巖、泥巖孔隙度。根據不同組分孔隙度變化范圍，可計算巖石總孔隙度上、下限。

相比于砂巖基質，泥巖孔隙度變化范圍較小。如圖4所示的W1井泥巖相孔隙度變化范圍為0～5%，砂巖相孔隙度變化范圍為5%～25%。結合圖3a、圖3b分析可知，泥質含量較低的巖相內的非線性特征較弱，限定孔隙度范圍并精確確定物性均值m0后，表現出近線性特征；泥質含量較高的巖相內雖然非線性特征較強，但是孔隙度范圍大幅收窄并精確確定m0后，其表現出弱非線性特征，此時的線性化近似成果精度可得到大幅提高。

通過式(19)計算得到巖石孔隙度上、下限，在此范圍內精確確定不同泥質含量條件下的物性均值m0，對圖3第一組正演模型開展巖相約束的Xu-White模型線性化近似。

由圖5可見，在W1井巖石孔隙度上、下限范圍內，泥質含量越大，巖石有效孔隙變化范圍越小。在有效孔隙范圍內，模型的非線性特征整體減弱。Xu-White模型和線性近似正演結果的吻合程度較高，預測效果得到改善。表明巖相約束巖石物理模型線性化近似方法可行、有效。

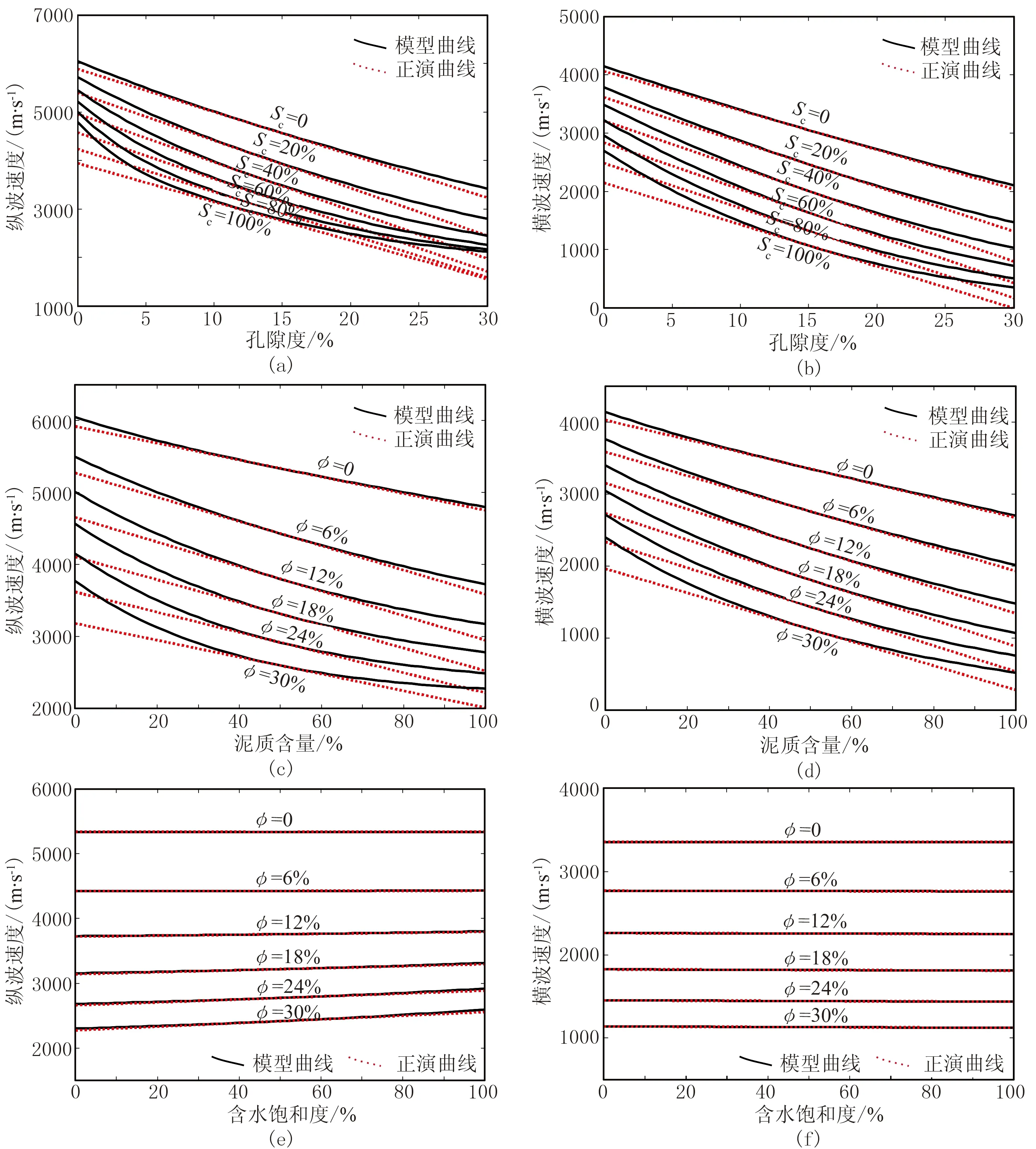
圖3 Xu-White模型與線性近似式正演結果對比

(a)不同泥質含量條件下縱波速度隨孔隙度變化，含水飽和度為100%； (b)不同泥質含量條件下橫波速度隨孔隙度變化，含水飽和度為100%； (c)不同孔隙度條件下縱波速度隨泥質含量變化，含水飽和度為100%； (d)不同孔隙度條件下橫波速度隨泥質含量變化，含水飽和度為100%； (e)不同孔隙度條件下縱波速度隨含水飽和度變化，泥質含量為50%； (f)不同孔隙度條件下橫波速度隨含水飽和度變化，泥質含量為50%

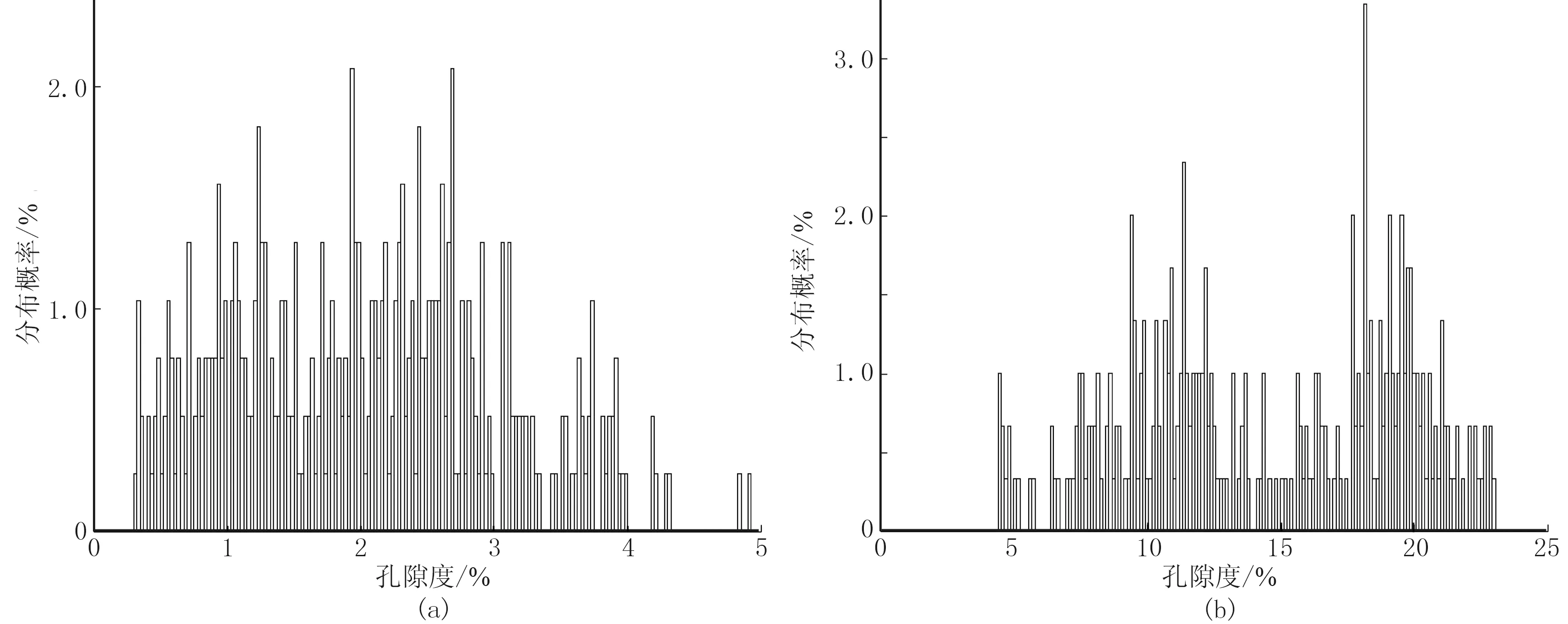
圖4 W1井分巖相孔隙度統計分析

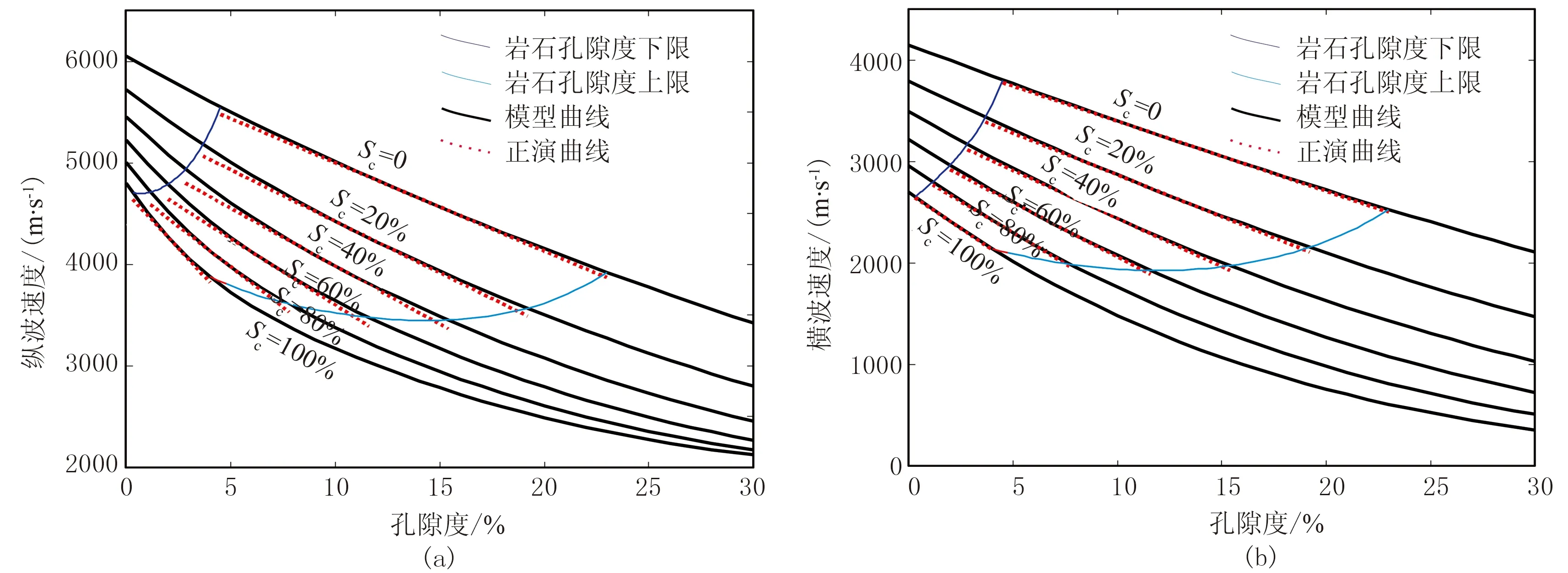
圖5 不同泥質含量條件下Xu-White模型與巖相約束線性近似正演結果對比

因此，在常規線性化近似方法式(17)的基礎上，提出巖相約束的Xu-White模型線性化近似方程

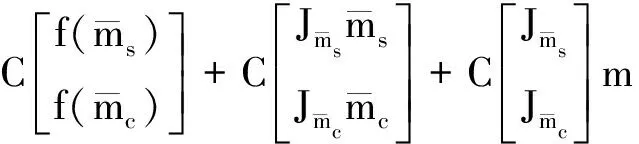
(20)

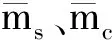
(21)

其中I為單位陣，而

(22)

式(22)中設定A中對角線元素ai為計算道中序號為i的樣點位置處的巖相系數，砂巖相中ai=1，泥巖相中ai=0。

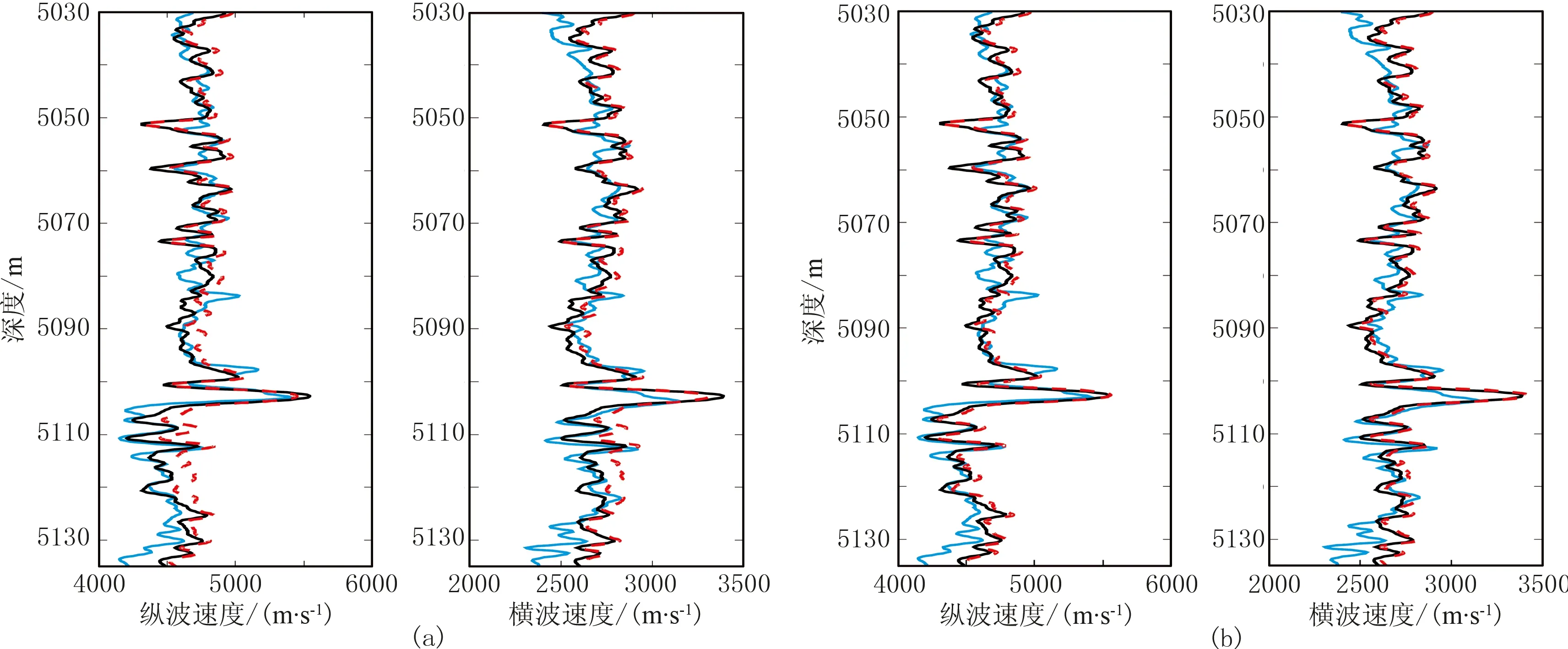
圖6 巖石物理模型線性化近似效果

將該方法用于實測曲線近似分析，效果如圖6所示，藍、黑、紅色曲線分別為實測、Xu-White正演及線性化近似結果。由圖可見，巖相約束的方法提高了線性化近似結果與Xu-White正演結果的吻合程度，進一步驗證了該方法的有效性，為后續實現儲層物性線性化反演奠定了基礎。

2 儲層物性線性化反演

2.1 反演目標函數

基于巖相約束的Xu-White模型線性化近似式(20)，采用貝葉斯理論構建儲層物性線性化反演目標函數。令

則式(20)可簡寫為線性化形式

d′=Gm+e

(23)

假設式(23)中的誤差項e與模型參數m均服從高斯分布，依據貝葉斯理論[26-27]，基于式(23)可構建后驗概率密度分布函數近似式

P(m|d′)?const×

(24)

式中： const為常量系數；Ce、Cm分別為誤差項e和模型參數m的協方差矩陣，與m0共同作為先驗信息(均由測井數據統計得到)約束求解過程，得到概率最大值。該過程一般通過求解下式最小值的方式實現，即

(25)

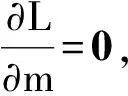
=m0+CmGT(GCmGT+Ce)-1(d′-Gm0)

(26)

式(25)的求解過程可看作最小二乘擬合過程，式(26)得到的解析解則為最小二乘最優估計值，即最終的反演結果。依式(24)推導反演參數協方差矩陣，用于分析反演結果的不確定性。即

(GCmGT+Ce)-1GCm

(27)

2.2 反演效果

為驗證線性化儲層物性反演方法的可行性及有效性，分別采用哈得遜油田一維測井數據W1(如圖2)與過該井的二維反演剖面進行測試。基于W1井所建立的巖石物理模型，將縱、橫波速度與密度曲線作為輸入，應用上述反演方法反演孔隙度、泥質含量及含水飽和度。反演過程采用巖相約束的孔隙度、泥質含量、含水飽和度等先驗物性數據，在巖相內選擇數據，統計數值范圍并計算數據均值，依據巖相內均值計算結果分別設定砂巖、泥巖段待反演物性參數m0。

圖7a為單井巖相曲線，用于約束反演過程。由圖7b可見實測曲線與反演結果趨勢基本一致，只在局部細節有所差異，差異主要是由模型線性化近似方法、巖石物理建模精度和測井物性曲線計算精度等共同導致。圖7c為反演結果的不確定性分析，藍色曲線為實測曲線，背景顏色為每個樣點對應的后驗概率密度分布。概率密度函數服從高斯分布，均值為樣點位置處的反演結果。方差值為對應的反演參數協方差矩陣對角線元素，由式(27)求取。方差值越大，概率密度分布范圍越大，反演結果不確定性越大。由圖可見，后驗方差從小到大依次為孔隙度、泥質含量和含水飽和度，說明孔隙度不確定性最小，反演精度最高； 泥質含量次之； 含水飽和度不確定性較大，反演精度較低。

基于疊前同步反演得到的縱、橫波速度及密度等彈性參數，采用巖相約束的儲層物性線性化反演方法，求取孔隙度、泥質含量與含水飽和度等物性參數，過W1井儲層物性反演結果如圖8所示。W1井在目的層系鉆遇薄砂層與東河砂巖兩套儲層，且東河砂巖儲層物性明顯好于薄砂層，與孔隙度、泥質含量反演結果相吻合。為進一步驗證反演效果，提取井點位置處的反演曲線(圖9)進行分析。

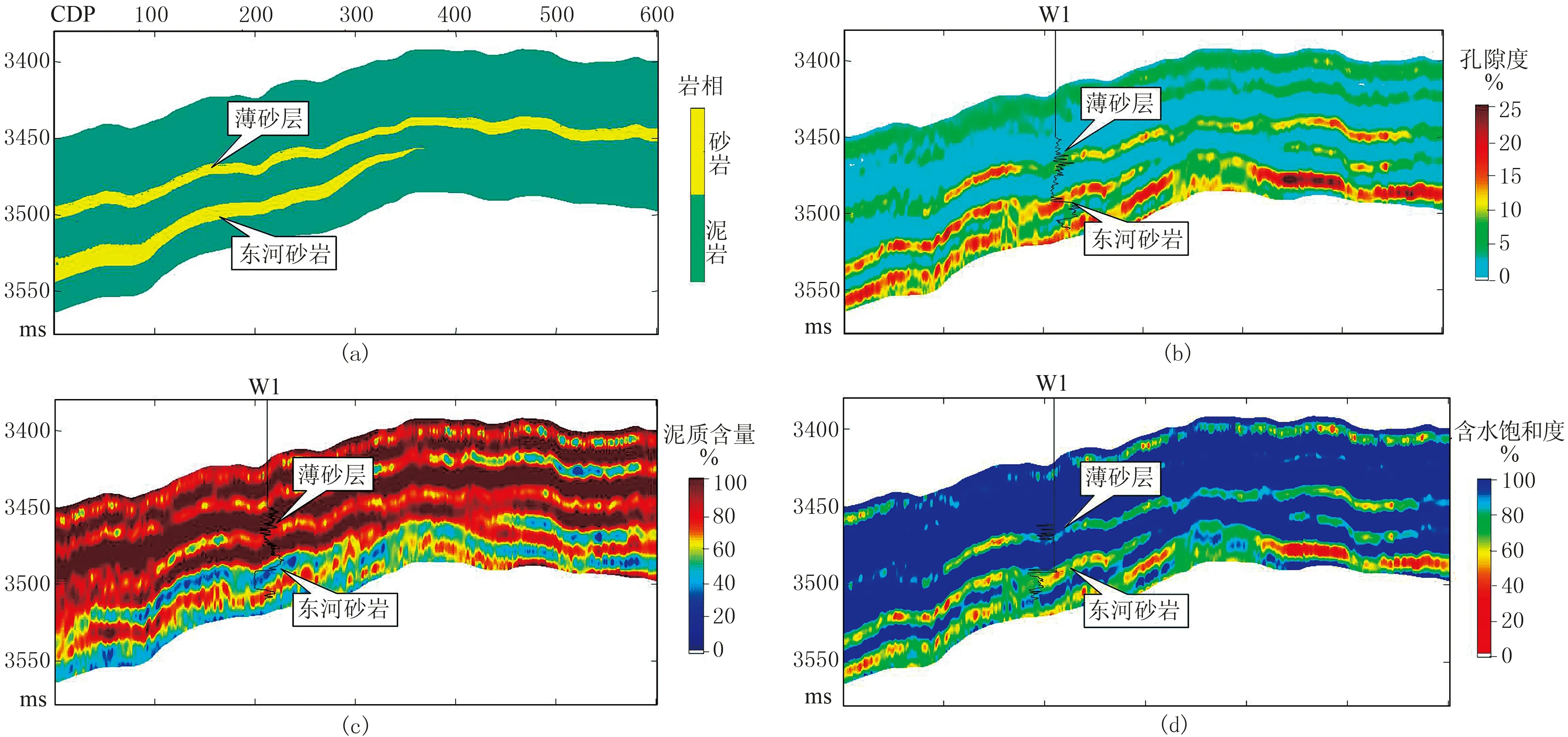
圖8 過W1井儲層物性反演剖面

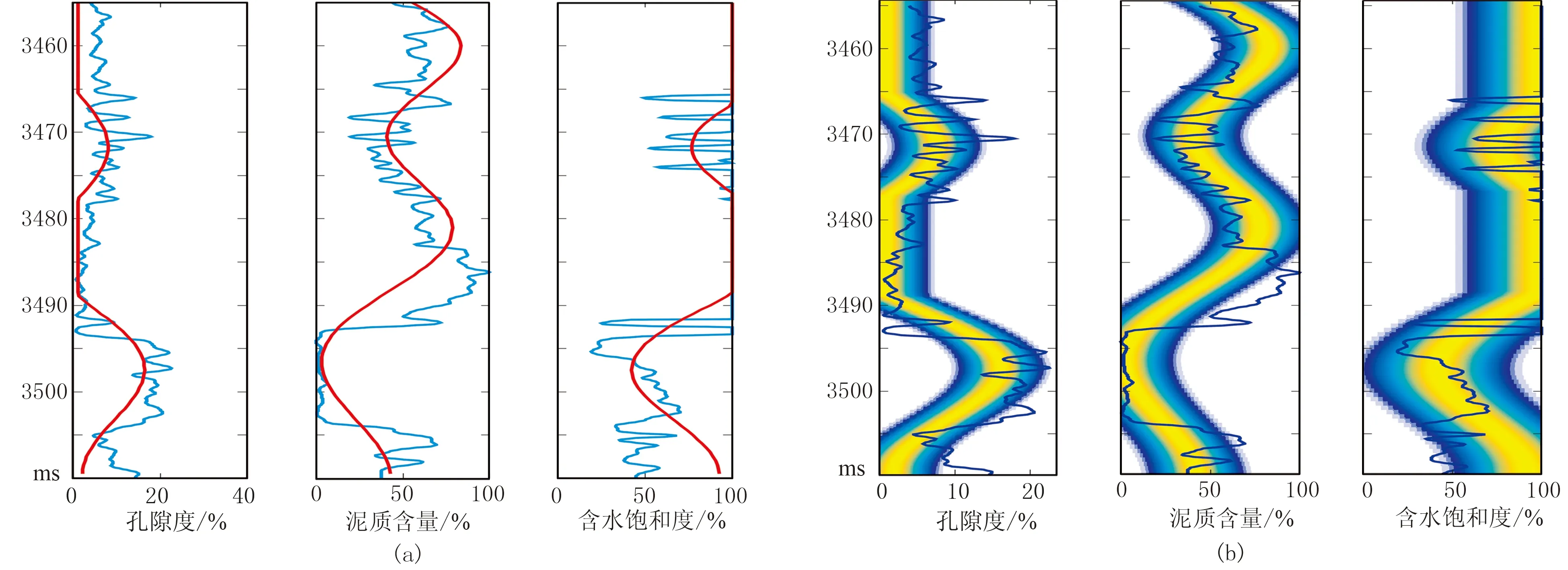
圖9 W1井點位置線性反演效果

由圖9a可見，實測曲線與反演結果趨勢基本一致，細節差異主要由地震資料分辨率所致。圖9b為不確定性分析結果，孔隙度、泥質含量不確定性相對較小，可靠程度較高，而含水飽和度反演不確定性相對較大。綜合分析表明，反演結果對儲層物性具有一定指示作用。

3 結論

針對Xu-White模型開展的正演分析表明，泥質含量為0時，該模型為近線性特征；隨著泥質含量增加，模型的非線性強度快速增大；泥質含量的大小是決定模型非線性強弱的關鍵因素。利用反映泥質含量的自然伽馬曲線劃分巖相，在不同巖相內確定實際數據分布范圍并求取儲層物性均值進行泰勒級數一階近似，可大幅改善巖石物理模型線性化近似的精度。

本文提出基于巖相約束的巖石物理模型線性化近似和反演方法，實現了Xu-White模型線性化求解儲層物性參數的反演過程，主要有四個步驟：①利用測井曲線建立巖相模型；②利用泰勒級數展開方法，分巖相線性化近似Xu-White模型；③依據貝葉斯理論分巖相建立儲層物性參數反演目標函數，并利用最小二乘優化算法得到孔隙度、泥質含量與含水飽和度反演結果；④通過不確定性分析，驗證反演結果的可信程度。該方法在模型試算及實際測試中，均取得了較高質量的反演結果，對孔隙度、泥質含量和含水飽和度等儲層物性參數具有一定指示作用。