利用反褶積廣義S變換提取流體流度屬性

劉 杰 張懿疆 王秀玲 曾紹剛 張文珠

(①中國石油大學(華東)地球科學與技術學院，山東青島 266580； ②中海石油(中國)有限公司深圳分公司，廣東深圳 518067；③油氣藏地質及開發工程國家重點實驗室，四川成都 610059； ④成都理工大學地球物理學院，四川成都 610059)

0 引言

隨著石油工業從增加產量轉向價值優化，石油行業對儲層預測的精度要求越來越高。由于儲層的滲流能力反映儲層品質，因此在評價中、深層優質儲層時，不能僅考慮孔隙度參數，而要同時兼顧滲透率、流體性質等其他因素。但迄今為止，人們還基本停留在通過研究滲透率的地震響應特征評價儲層[1-2]，而很難基于地震資料反演滲透率或預測儲層。因此，近年來人們將目光逐漸由滲透率轉向儲層流體的可動性，如流體流度屬性可很好地表征流體的可動性。有人[3-5]以滲流理論為基礎首次推導了飽和流體彈性介質波動方程，并證明該方程與試井分析中常用的Frenkel-Gassmann-Biot多孔彈性模型、壓力擴散模型[6]相關，最終得到飽和流體儲層低頻域反射系數漸近表達式，認為低頻反射系數正比于流體流度(Fluid Mobility，又稱遷移率)、巖石體積密度、地震信號頻率的平方根。Goloshubin等[7-8]應用流體流動性和散射機制，推導出與地震頻率相關的流體流度屬性，并用該屬性預測儲層中流體的流動能力和滲透率。Chen等[9]基于實際地震資料的流體流度屬性識別流體，取得了較好的效果。張生強等[10]基于高分辨率反演譜分解近似計算流體流度屬性，進一步提高了流體流度屬性剖面的分辨率。其中高分辨率反演譜分解使用稀疏反演算法將地震資料投影到分頻子波庫，再將所得結果進行重排，從而得到一個稀疏的時頻譜,其實質仍是一種分頻方法。

由于在流體流度屬性計算過程中，需要計算地震數據的瞬時振幅譜，不同時頻分析方法獲得的流體流度屬性剖面的分辨率存在差異，進而影響儲層預測精度。因此為提高儲層預測精度，有必要選擇時頻分析方法以獲得高分辨流體流度屬性剖面。小波變換(WT)繼承和發展了短時傅里葉變換局部化的思想，同時能夠提供一個隨頻率改變的“時—頻”窗口，是信號時頻分析的較理想工具，但小波變換的結果是時間—尺度譜，而非時頻譜。為此，Stockwell等[11]提出了S變換，S變換不僅反映信號在頻率域的變化，而且可以實現無損重構。為了使窗函數更靈活，人們又提出了廣義S變換，如陳學華等[12-14]引入了兩個調節參數λ、p，可根據實際地震資料分解尺度的需要靈活調節，以使地震資料的分辨率達到所需的分析尺度。與小波變換相比，S變換、廣義S變換等引入信號頻率參數控制窗口尺度，其變換結果是更為直觀的時間—頻率譜，便于分析信號的頻率特征。受測不準原理的制約，以上變換的時頻譜分辨率仍然有限。Wigner-Ville分布作為一種非線性時頻分析方法，擺脫了測不準原理的制約，但對于復雜信號會產生交叉項干擾[15]。Lu等[16-17]提出反褶積短時傅里葉變換，不僅提高了時、頻分辨率，且減少了交叉項干擾。朱恒等[18]首次利用反褶積短時傅里葉變換提取單頻剖面預測薄儲層。張懿疆等[19]首次利用反褶積廣義S變換分析薄儲層的低頻伴影，取得較好的效果。本文利用反褶積廣義S變換提取流體流度屬性，通過仿真試驗和實例試算驗證了方法的有效性和實用性。

1 方法原理

1.1 流體流度屬性的定義及提取方法

Korneev等[3]、Silin等[4]、Goloshubin等[8]推導了飽和流體介質在低頻域地震響應的反射系數線性漸近表達式。平面縱波在干巖石與飽含流體彈性介質界面上的反射系數為

(1)

式中： i為虛數單位；R0和R1是實系數，為反映巖石和流體特性的函數，包括孔隙度、密度和彈性系數信息；κ為儲層滲透率；η為流體黏滯系數；ρb為儲層內流體的密度；ω為低頻地震信號的角頻率。

將式(1)對ω求導，得

(2)

Goloshubin等[7]在低頻漸近分析理論的基礎上提出了成像屬性的概念，即

(3)

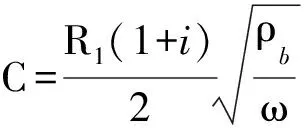
(4)

(5)

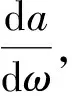
1.2 優勢頻率及基質體積模量的求取

在求取流體流度屬性過程中，需要求取峰值頻率，Silin等[5]在推導縱波入射滲透地層的反射理論公式時，獲得了快縱波反射共振峰值頻率

(6)

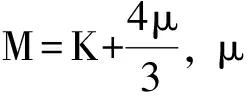
式中：Ksg和Kfg分別為骨架的體應變和流體壓力變化造成的基質顆粒壓縮，把顆粒體應變與骨架應力、流體壓力聯系起來；Kg為基質體積模量；φ為孔隙度；K為干巖石體積模量。以上各參數中，Kg最難求取。為此，本文采用賀錫雷[20]的LRM線性擬合法求取Kg。通過對Biot-Gassmann流體替換方程進行合理改造，可獲得其近似公式。考慮到難以直接由測井資料獲得骨架模量或干巖石模量以及孔隙結構明顯影響巖石有效彈性模量等因素，將含有孔隙結構信息的干巖石橢球包體近似公式引入流體替換方程近似式，與常規計算巖石基質模量的方法相比，LRM法簡單易行且精度較高。圖1為根據南海A區巖石物理參數得到的壓縮系數(體積模量的倒數)—孔隙度交會圖。根據LRM方法可知，壓縮系數為截距B(在負半軸，取絕對值)與斜率A的比值。表1是據A區54塊巖樣計算的壓縮系數及擬合系數A、B。由表可見，巖樣飽和不同流體求出的壓縮系數基本是一致的，在實際計算過程中取平均值即可。

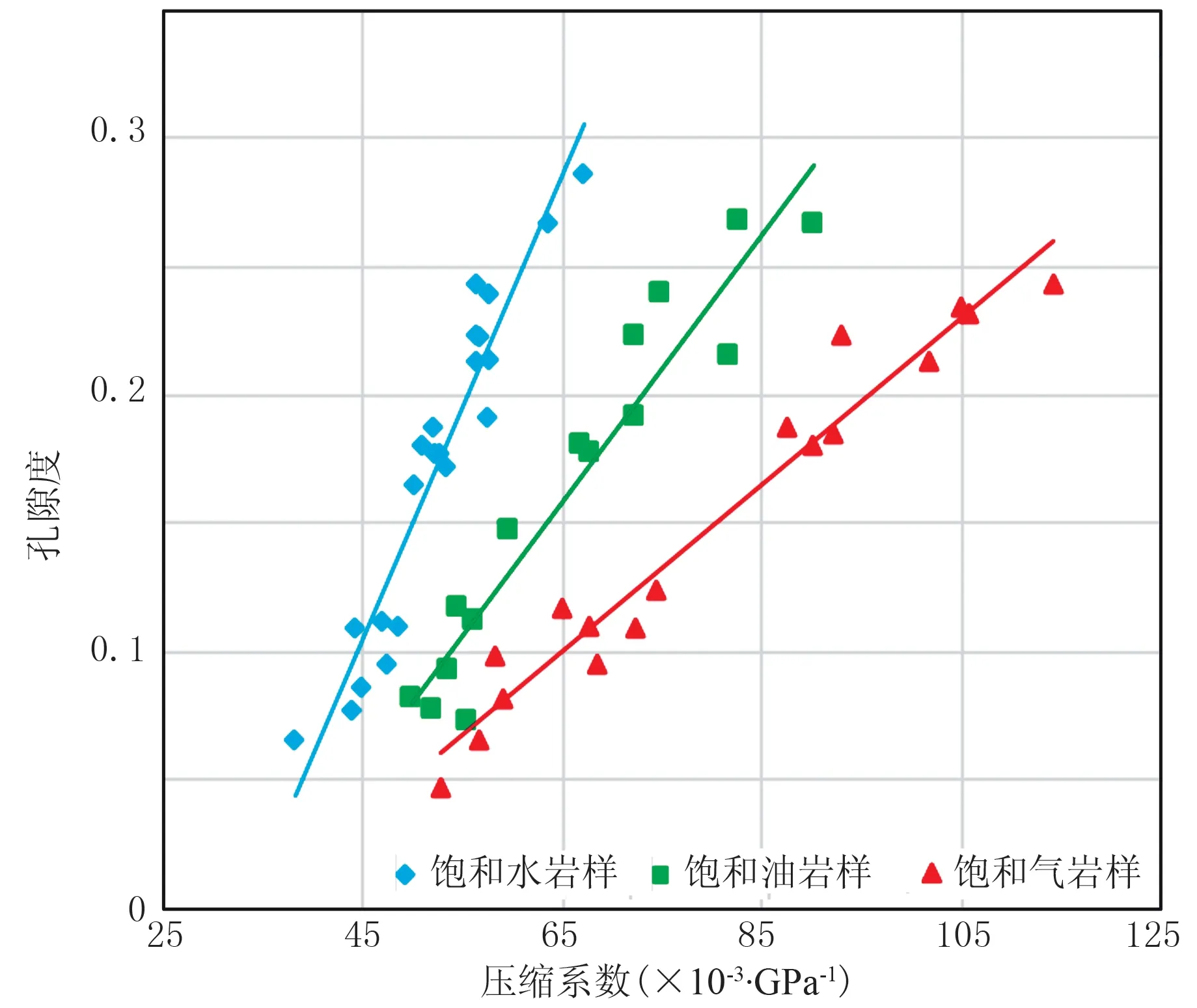
圖1 壓縮系數—孔隙度交會圖

巖樣類別塊數系數A系數B壓縮系數飽和水巖樣220.0090.300533.3889飽和油巖樣150.00520.179734.5577飽和氣巖樣170.00320.110934.6563

1.3 反褶積廣義S變換

陳學華等[12-13]引入高斯窗函數的調節參數λ>0、p>0 ，通過調節λ、p改變高斯窗隨頻率的變化趨勢，從而靈活地分析、處理具體信號。對于信號x(t)，其廣義S變換可表示為

(7)

式中：τ為用于確定分析時窗的時間位移；f為頻率。

廣義S變換譜為原始信號與高斯窗各自的Wigner-Ville分布的二維褶積，即

WVDh(t-u,f-v)dudv

(8)

式中： WVDx為原始信號x(t)的Wigner-Ville分布(簡寫為Wx)； WVDh為高斯窗h(u)的Wigner-Ville分布(簡寫為Wh)。本文采用非線性的迭代復原反褶積算法——Lucy-Richardson反褶積算法[16-17]計算廣義S變換譜，其表達式為

(9)

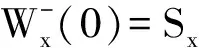
2 仿真實驗

首先利用合成信號驗證廣義S變換、反褶積短時傅里葉變換、反褶積廣義S變換的時頻分析效果。合成信號x(t)為由3個線性信號疊加而成的時變信號，即

(10)

圖2為合成信號及利用不同分析方法得到的時頻譜。由圖可見：利用廣義S變換得到的時頻譜中頻率發生突變的位置(紅色箭頭所示)不清晰(圖2b)；對信號做反褶積短時傅里葉變換得到的時頻分布的邊界相對清楚(圖2c)，但仍不明顯；對信號做反褶積廣義S變換得到的時頻分布(圖2d)較好地區分了不同頻率成分的信號，顯示出較高的時頻分辨率與時頻聚集性。

利用黏滯—彌散波動方程進行數值模擬，該方程是一種考慮流體黏滯性和彌散性的聲波方程，可以很好地體現含流體儲層對不同頻率地震波的衰減特性[21-23]。圖3為透鏡體儲層模型及由不同方法得到的流體流度屬性剖面。由圖可見：基于反褶積短時傅里葉變換得到的儲層流體流度剖面中目的層的高流體流度屬性區域與透鏡體位置不完全對應(圖3c)；基于反褶積廣義S變換得到的儲層流體流度剖面中高流體流度屬性區域與透鏡體的位置較為一致，尤其對透鏡體儲層兩側尖滅點刻畫較好，驗證了方法的高分辨率特性(圖3d)。

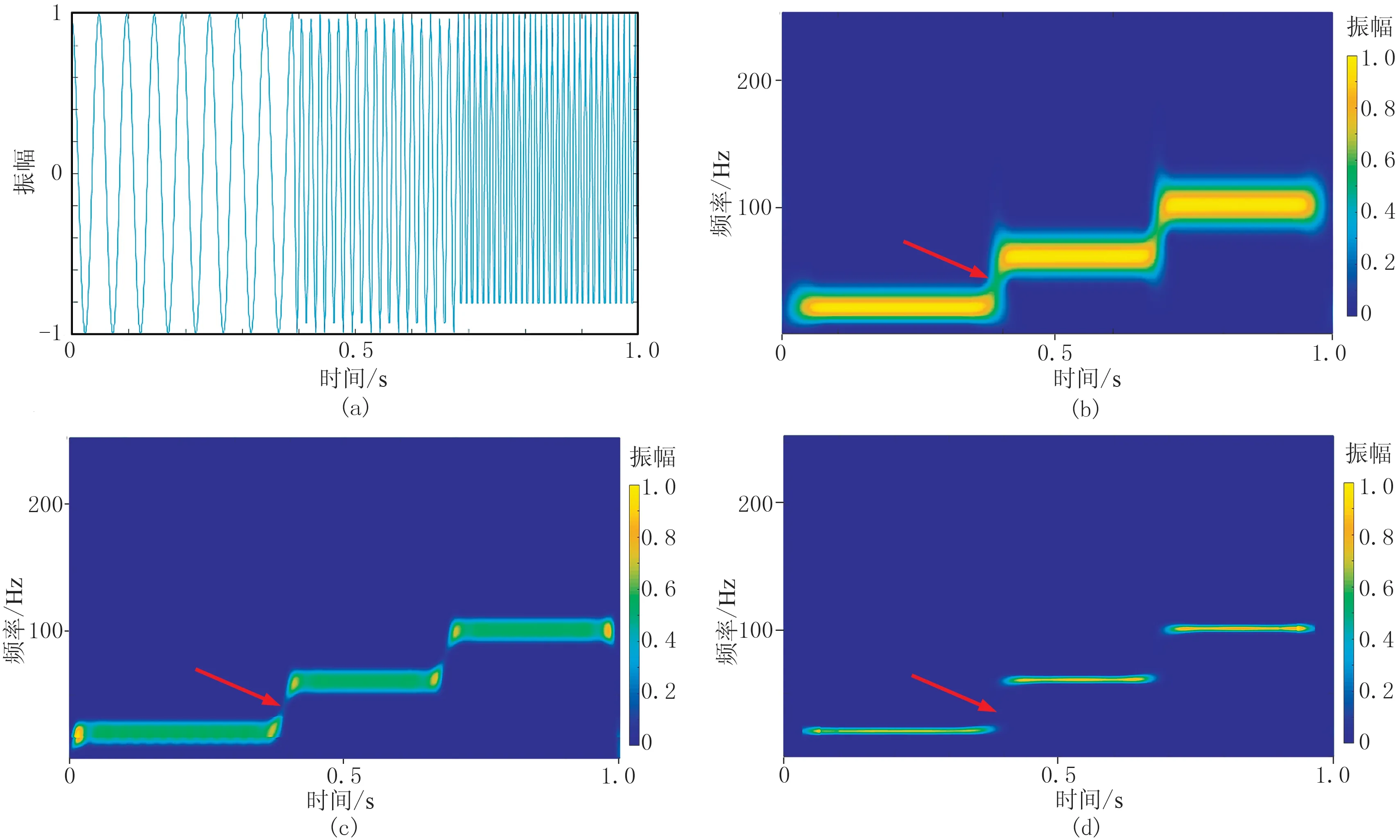
圖2 合成信號及利用不同分析方法得到的時頻譜

圖3 透鏡體儲層模型及由不同方法得到的流體流度屬性剖面

3 實例分析

為了進一步驗證文中方法的實效性，從南海A區的地震數據中提取了流體流度屬性。該區位于南海北部陸坡前緣，處于長源富砂珠江組下方，是深水勘探的有利地區，已發現多個油氣田和具有潛在商業價值的含油氣構造。工區內儲層縱波速度約為3500～4200m/s，地震資料主頻為25～30Hz，砂體平均厚度約為30m。地溫梯度、埋深、成巖作用類型及強度共同控制砂巖儲集性能的優劣。研究區優質儲層埋深變化較大，主要分布范圍為1000～3000m，地溫梯度G分布范圍為3～7℃/100m。在低地溫梯度條件下(G<4℃/100m)，儲層原生、次生孔隙發育，滲透率較大，即使埋深達3000m時孔隙度也可達到15%，滲透率可達數十毫達西；在中、高地溫梯度(G≥4℃/100m)條件下，儲層次生孔隙發育、原生孔隙次之，形成中孔、低滲儲層。工區橫向地溫梯度及縱向埋深差異造成強烈的儲層物性非均質性，致使儲層物性評價面臨巨大挑戰。

圖4為A—B—C—D—E—F井連井地震剖面，圖5、圖6分別為利用廣義S變換和反褶積廣義S變換獲得的流體流度屬性剖面。由圖可見：由于流體在砂巖中的流動性較高，對應于高流度屬性值(圖5、圖6)；基于廣義S變換的流體流度屬性剖面雖然在儲層位置呈流體流度屬性高值，但高值區域的儲層厚度大于井中解釋的儲層厚度(橢圓區域所示)，即剖面的分辨率不高(圖5)；基于反褶積廣義S變換的流體流度屬性剖面高值區與儲層解釋結果吻合很好，具有較高的分辨率(圖6)。

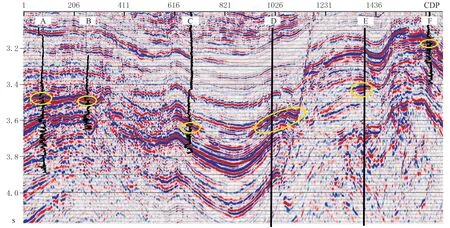
圖4 A—B—C—D—E—F井連井地震剖面

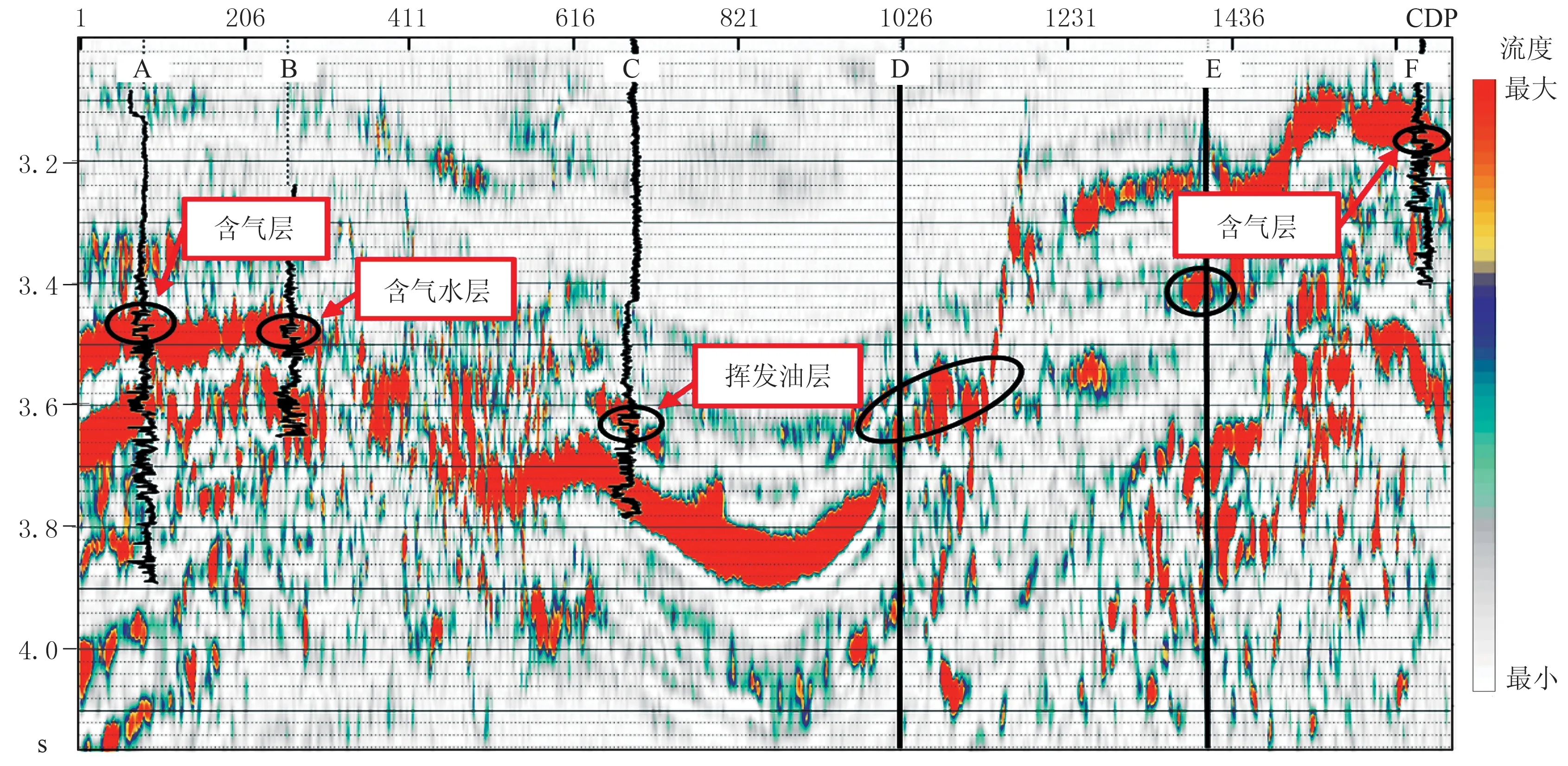
圖5 廣義S變換獲得的流體流度屬性剖面

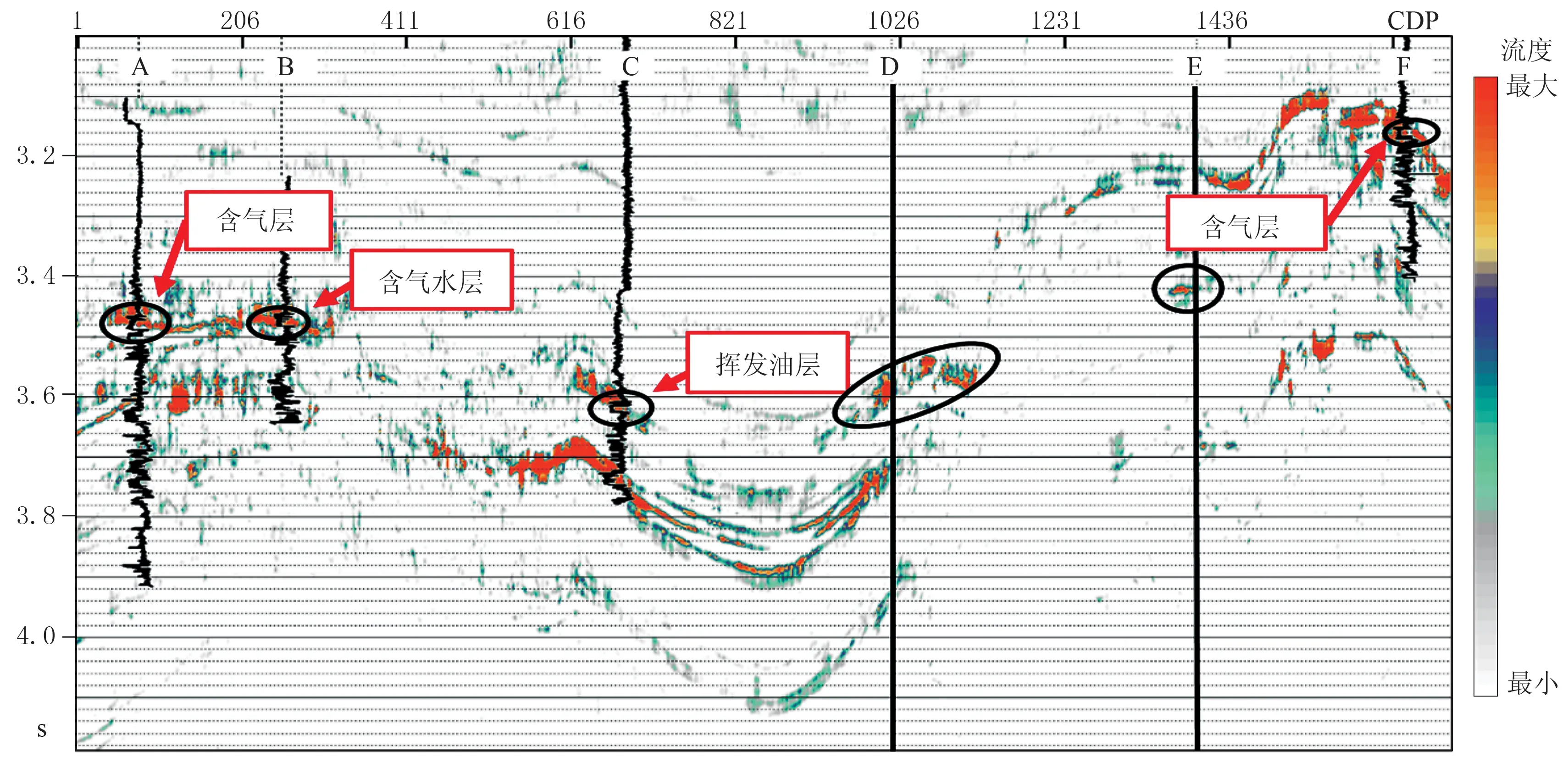
圖6 反褶積廣義S變換獲得的流體流度屬性剖面

4 結束語

(1)與廣義S變換相比，反褶積廣義S變換的時頻分辨率與頻率聚集性進一步提高，適合處理具有時變特征的地震數據。

(2)Goloshubin流體流度屬性與儲層滲透率和流體黏滯系數具相關性，在理論上表征了儲層流體的活動能力。實例分析展示了由地震數據得到的流體流度屬性預測儲層的可行性。

(3)精確獲取地震頻率信息是獲得高精度流體流度屬性的關鍵，不同時頻分析方法獲得的流體流度屬性剖面的分辨率存在一定差異，本文通過引入反褶積廣義S變換，提高了流體流度屬性剖面的分辨率。

尚需指出，流體流度屬性目前在流體性質識別方面上存在一定缺陷，因此需結合其他方法(如疊前反演或AVO分析)評價儲層。