艦炮供彈系統動力學仿真分析

葛勝利

(中國船舶重工集團公司第七一三研究所，河南 鄭州 450015)

0 引 言

傳統艦炮設計理論對艦炮的運動和受力進行分析時，多基于“平面、對稱及靜平衡”3個基本假設[1]。因此，在對艦炮進行建模與分析時，雖然引入了多種經驗系數，但仿真結果與實際仍有較大差異。出現上述現象的原因在于，傳統的分析方法實際上是準靜態的分析方法，而艦炮實際工作時，是一個受沖擊的過程，應采用多體系統動力學的方法進行分析。隨著現代火炮設計理論與方法的發展，基于虛擬樣機技術的設計越來越受到重視，是未來火炮設計理論與方法的發展趨勢。例如美國TACOM公司提出利用虛擬樣機技術支持3 200多種武器系統的研制，依據武器系統的虛擬樣機可以在物理樣機制造之前，全面掌握武器潛在的各種問題，提出設計變更和設計反饋，減少設計失誤和實物試驗驗證次數。

虛擬樣機技術是一種新型的產品設計和過程開發的方法，虛擬樣機模型包含了產品全壽命周期設計的信息，包括物理樣機的幾何信息、材料信息和供仿真分析的數學模型信息，這種模型實際上是一種設計、分析一體化的模型，可用來分析和評估系統的性能，為物理樣機的設計和制造提供參考依據。虛擬樣機開發過程如圖1所示。

圖1 虛擬樣機開發過程Fig.1 Virtual prototype development process

建立一個全面反映艦炮的工作過程并準確描述各零部件運動和受力的動力學模型，是解決艦炮仿真問題的重要步驟。虛擬樣機技術是將機械系統作為一個整體進行考慮，外部影響通過作用力和驅動約束等元素施加于系統，可以準確地分析系統內部構件之間的關系與作用[2]。本文探討了虛擬樣機技術在某艦炮供彈系統設計中的應用，通過在PRO/E環境下建立的三維參數化模型，在ADAMS中建立供彈系統的虛擬樣機模型，并進行動力學仿真研究，得到主要傳動件的動力學數據。然后利用已經建立的彈鼓運動阻力參數檢測裝置對供彈系統樣機進行了試驗，通過該裝置的數據采集系統，輸出射擊狀態下彈鼓運動速度、輸入扭矩等參數曲線，其變化趨勢及最終狀態與仿真計算數據基本吻合，充分證明了計算結果的可信性。

1 供彈系統工作原理

某型艦炮的彈鼓式無鏈供彈系統是1套大容量、能夠連續快速供彈、結構緊湊并具有多彈種更換功能的系統平臺，其機械結構簡圖如圖2所示。

供彈系統動力由自動機提供，經過齒輪箱中4級齒輪和太陽輪運動傳遞至行星輪，行星輪的公轉帶動內鼓旋轉將炮彈從內鼓輸出，經齒輪箱各級撥彈輪輸入炮膛。

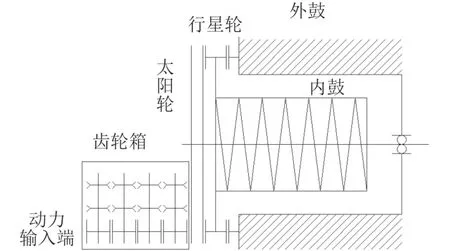
圖2 供彈系統結構簡圖Fig.2 Schematic diagram of the structure of a projectile supply system

2 建立供彈系統虛擬樣機模型

本文利用PRO/E軟件建立模型，根據供彈系統機械結構，建立三維模型。在PRO/E中裝配時，要檢查裝配模型的干涉情況，以減小仿真分析時，由模型初始狀態所引起的誤差。彈藥傳遞過程中存在復雜的接觸碰撞關系，仿真不但要求得到機構的運動規律，還要能夠得到運動過程中零件間的相互作用，以更好的模擬零件的真實工作狀態。對于建好的三維模型，首先需要對模型進行校核，檢查裝配模型是否存在干涉，若存在需對模型進行局部修改或者重新裝配，其次在建立動力學模型過程中需對模型進行適當的簡化處理，如一些不影響仿真結果的零件（如螺栓、螺母等）和一些不關心的部件（如機箱），可直接刪除，這樣可以降低求解資源、節省計算時間。

該模型全面反映了機構的幾何特征，包括各部分的尺寸、各幾何體之間的連接關系和裝配關系。

建立模型的步驟如下：

1）在PRO/E中裝配好三維實體模型后，將模型導入ADAMS中；

2）在ADAMS中設置重力在-Y方向，并設置每個部件的密度，使其具有轉動慣量[4]。

3）機架以及不參加運動的部件和大地建立固定副，齒輪添加轉動副。兩齒之間添加接觸副，接觸參數設置為：k=1.1×10E9，e=1.5，δ=45，C=0.01。設置轉動副和接觸副摩擦系數；并通過軟件檢查機構自由度驗證動力學模型的可解性，對模型中的過約束進行修改。添加完約束必須進行機構檢查（model verify），必須確保沒有過約束，否則仿真會產生不可預料的結果。特別對于封閉機構（如曲柄滑塊機構），ADAMS一定會產生過約束，此時要用基本約束副代替旋轉副或滑動副。

4）根據實際試驗中自動機射速，在輸入軸上施加轉速驅動。模擬轉速曲線如圖3所示。

將實驗得到的每2發彈發射間隔轉換為星形體的轉速，將轉速添加在底部曲柄連桿機構的大錐齒輪上，從而給整個機構提供動力。由于實驗中每兩發彈發射間隔時間是變化的，故需將轉速數據導入到ADAMS中，用AKIMA插值擬合發進行擬合，得到曲線，并將轉速曲線加載到錐齒輪上，由錐齒輪帶動星形體運動，同時錐齒輪與五齒齒輪嚙合，帶動撥彈軸運動，從而給撥彈輪傳遞動力。供彈系統的虛擬樣機模型如圖4所示。

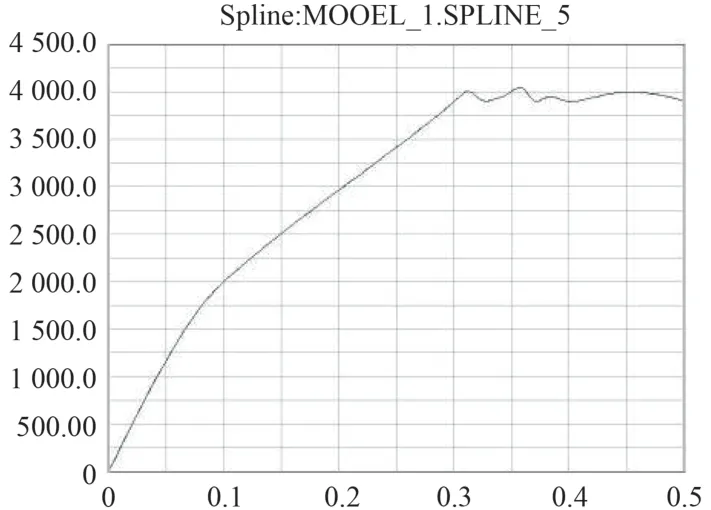
圖3 模擬轉速曲線Fig.3 Simulated rotational speed curve

圖4 彈鼓虛擬樣機模型Fig.4 Virtual prototype model of missile and drum

5）仿真計算

建好虛擬樣機模型后，選擇求解器并確定分析時間及步長，即可進行仿真計算。

3 動力學仿真分析

本文主要分析艦炮發射過程中，從啟動到運行平穩這個階段，考慮了彈鼓中不裝彈空載和裝滿彈滿載2種情況。內鼓轉動速度決定了供彈系統的供彈速度，進而影響自動機發射率。這段時間內彈鼓旋轉角速度和角加速度變化情況如圖5和圖6所示。

整個過程處于加速階段，因此齒輪上的作用力較大。運動經由齒輪箱最后一級齒輪與太陽輪的嚙合傳入彈鼓，此處處于傳動鏈的中間位置。本文采集此處的嚙合力曲線如圖7所示。

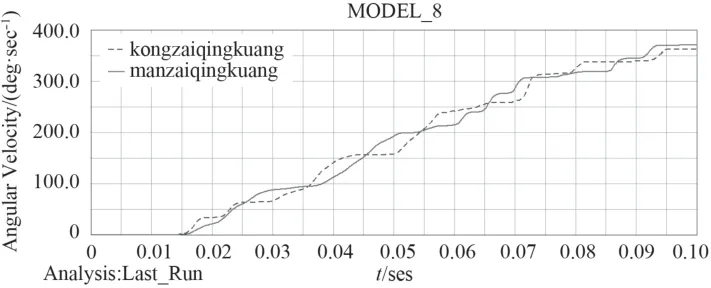
圖5 2種情況下彈鼓角速度Fig.5 Projectile angular velocity in two cases

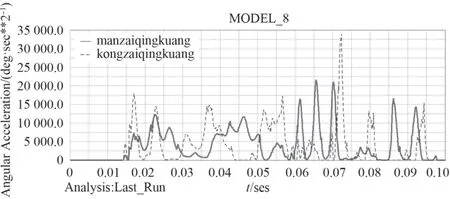
圖6 2種情況下彈鼓角加速度Fig.6 The acceleration of the blast angle in two cases

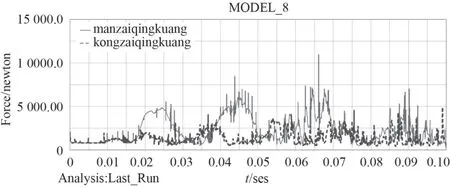
圖7 嚙合力曲線Fig.7 Meshing force curve

供彈系統啟動加速過程中，扭轉力矩迅速增大，隨著啟動過程結束，供彈系統旋轉速率穩定，扭轉力矩經歷正弦式波動后逐漸趨于平緩，最后圍繞一個較小值在小范圍內正弦波動。如圖8所示。

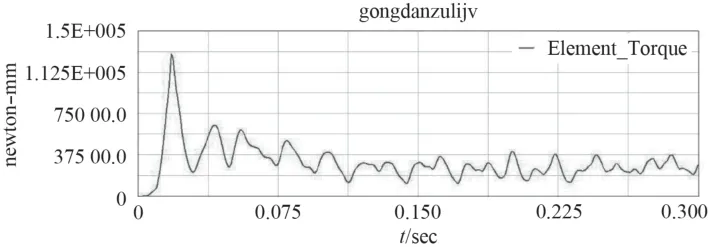
圖8 彈鼓啟動力矩Fig.8 Start torque of a drum

圖5中彈鼓角速度增加基本一致，但滿載情況下上升較為平緩，空載情況下曲線出現尖點拐點。從圖6中可以看出，空載情況下的彈鼓角加速度變化劇烈，滿載情況下較為穩定，同時印證空載情況下受力波動較大。空載時，角加速度最大值出現在0.072 s附近，滿載時在0.06—0.07 s內連續出現3次峰值。此時嚙合力在7 000 N附近波動，并在0.066 s出現最大值。在0.095 s后，角加速度趨于0，角速度達到最大值，運行趨于平穩。由圖7可以看出，空載情況下，受力波動較大，這時輪齒受到較嚴重的沖擊。在速度達到最大值并將穩定運行時，嚙合力仍以較大幅度波動，末端反而出現一個最大受力。滿載情況下，受力波動較小，但是受力較大，最大值接近11 000 N。在速度達到最大值并穩定運行時，受力逐漸減小趨于穩定。由圖8可以看出彈鼓啟動力矩最大值為125 N·m，射速穩定后輸入扭矩25 N·m。

4 試驗驗證

彈鼓運動阻力檢測裝置主要用于研制內能源轉管自動機帶動彈鼓供彈系統的能源匹配試驗、彈鼓運動阻力矩檢驗和可靠性試驗，可以進行模擬試驗和動態特性的測試，確定彈鼓供彈系統的阻力距特性、供彈的可靠性以及其他特性，為該產品的檢驗提供試驗數據和技術參數。彈鼓運動阻力檢測裝置主要由彈鼓阻力矩及運動狀態測試系統、彈鼓運動控制系統、炮彈運動及加速度存儲測試系統、數據采集及分析系統等4部分組成，如圖9所示。

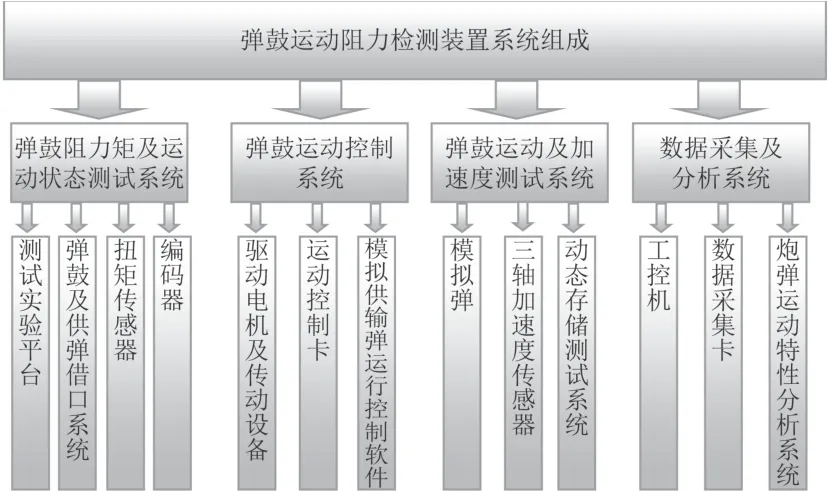
圖9 彈鼓運動阻力檢測裝置Fig.9 Resistance detection device for drums and drums

按照4 200發/min射速設置試驗裝置狀態，彈鼓運動角速度曲線如圖10所示，輸入扭矩曲線如圖11所示。

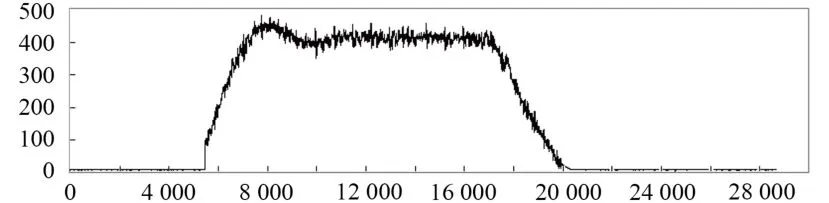
圖10 彈鼓運動角速度Fig.10 Angular velocity of projectile and drum motion

圖11 輸入扭矩Fig.11 Input torque

試驗過程模擬了滿載情況下，該型艦炮射擊時供彈系統動力學參數，由于仿真計算步數限制，得到的彈鼓運動角速度曲線較短，沒有顯示出穩定狀態，但其基本趨勢及最大值等數據與試驗數據一致。試驗過程中，在停射時輸入扭矩會有一個突然增大的波峰，這是由于緊急制動造成的，其變化趨勢與仿真計算結果也基本一致。

5 結 語

在射擊起始階段，空載情況下的供彈系統齒輪嚙合力波動較大，產生較大的加速度，因此振動較大；滿載情況下的齒輪嚙合力大，加速過程相對空載時較平穩。通過模擬射擊試驗，試驗數據與仿真計算數據基本一致。根據以上供彈系統動力學分析結果，可以為供彈系統的強度校核、結構優化提供較為可靠的分析依據。