基于CUDA的KNN算法并行化研究
劉端陽,鄭江帆,劉 志
(浙江工業大學 計算機科學與技術學院,杭州310023)
1 引 言
分類技術在許多領域得到廣泛應用,比如人工智能,網絡入侵檢測等.分類技術是把未知分類的樣本數據經過一系列模型之后分到若干已知分類的過程[1].它先通過已有的訓練數據集進行學習和分析,從這些數據的分布中找出分類的規律,逐步優化分類的模型,從而判斷新數據屬于哪個類別.K最近鄰(KNN:K-Nearest Neighbor)算法[2]是最為流行的分類算法之一,廣泛應用于數據分析、圖像處理、文本分類[3]等領域.KNN算法在距離計算階段需要計算每個測試數據點到所有訓練數據點的距離,距離排序階段需要對距離向量進行排序.如果任務的測試數據總量為m,訓練數據總量為n,數據的維度為d,則距離計算的時間復雜度為O(mnd),排序階段的時間復雜度為O(mnlogn).隨著測試數據集和訓練數據集規模的增加,算法的時間成本也會成倍增長,無法滿足大數據時代下的快速計算需求.因此對于計算密集型的KNN算法,運用CUDA(Compute Unified Device Architecture)并行化該算法,能夠節省大量計算時間.CUDA是NV-IDIA公司推出的通用并行計算架構,它采用GPU(Graphics Processing Unit)來解決復雜計算問題.CUDA提供了硬件的直接訪問接口,并不依賴傳統的圖形API,實現GPU的訪問,降低了圖形處理器的編程難度.
國內外已經有很多基于CUDA架構的KNN以及其他算法的并行化研究,Jian等[4]將輸入的數據分組,在每個組內進行并行計算,然后得到每個組的top-K元素隊列,最后合并每個組得到全局的K個近鄰,該方法降低了距離排序的時間復雜度,但是在距離的計算階段并行度不高.Garcia等[5,6]將KNN的暴力搜索算法并行移植到GPU中執行,在距離計算階段使用了分塊的矩陣乘法,具有良好并行性,但是在距離排序階段時間復雜度較高.Dashti等[7]在面對高維度數據時合理使用線程加速距離計算,并且在GPU中并行實現了三種距離排序方法,但是當訓練集數據量很大時排序階段的加速效果有限.Masek等[8]和王裕民等[9]使用多塊GPU設備搭建了一個GPU集群,利用GPU的集群優勢對KNN和卷積神經網絡算法進行加速,該方法可以處理更加龐大的數據集,不過提高了硬件成本.Liang等[10]提出cuKNN算法,采用數據流的方式對輸入數據進行計算,利用共享內存加速每個測試數據距離向量的排序,能夠批量處理輸入數據的同時也提升了性能.Barrientos等[11]提出基于CUDA的窮舉排序算法解決KNN問題,在K值較高的情況下也有良好的加速比.Mayekar等[12]提出一種并行的KNN方法快速解決字符識別的問題,并且能保持較高的準確率.
基于上述國內外的研究現狀,本文提出了新的KNN并行化算法(即GS_KNN).新算法充分利用了CUDA函數庫以及內存體系,將算法的所有計算過程都移植到GPU中,發揮其良好的運算能力.在運算量最大的距離計算階段,將測試數據集和訓練數據集存儲在CUDA全局內存中,使用Cublas函數庫的通用矩陣乘計算,提高了運算速度.在距離排序階段,針對k值的大小提出了兩種優化策略,分別是基于k次最小值查找的最近鄰選擇和基于雙調排序的最近鄰選擇,降低了時間復雜度.在決定分類標號階段,采用了CUDA內部的原子加法操作,GPU全程參與計算,從而提高了整體性能.最后通過實驗證明,在保證算法魯棒性的前提下,獲得了良好的加速效果.
2 背景知識
2.1 KNN算法
KNN算法是目前最為流行的分類算法之一,該算法是一種基于距離的分類,通過計算測試數據與訓練數據之間的距離或者相似度來進行分類,同一類別的內部數據之間具有較高的相似度,而不同類別之間數據相似度較低.現有R={r1,r2,…,rn}是一個擁有n個點的輸入訓練集,其中每個點的數據維度為d,即rj=(rj1,rj2,…,rjd),而S=(s1,s2,…,sm)是與R在同一個維度空間上的輸入測試集.KNN算法的目標是對于每一個si∈S,搜索距離si最近的k個R數據點,然后根據這k個數據點的類別判斷si的類別.如圖1所示,表示一個R大小為15,k等于4的查詢例子.
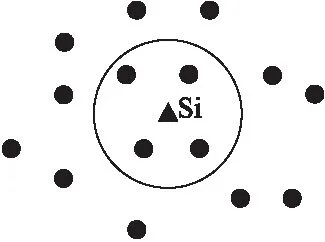
圖1 KNN查詢示例Fig.1 KNN query example
求解KNN算法最經典的方法就是通過暴力搜索解決,具體算法過程如算法1所示.
算法1.基于CPU的串行KNN算法
輸入:包含n個點的帶有分類標號的訓練數據集R;包含m個點的無分類標號的測試數據集S;最近鄰個數k.
輸出:m個測試數據的分類.
1)計算測試集S中點si到所有rj的距離.
2)對步驟1得到的n個距離進行升序排序.
3)根據排序結果,選擇前k個最小距離,得到距離點si最近的k個訓練數據.
4)統計這k個訓練數據的分類標號,出現次數最多的那一個標號即為點si的分類.
5)循環步驟1至4,一直到m個測試數據的分類計算完畢.
由于數據維度為d,步驟1(即距離計算階段)的時間復雜度為O(nmd),步驟2(即排序階段)的時間復雜度為O(mnlogn).步驟4(即決定分類標號階段)的時間復雜度為O(mk),此值較小,可忽略不計.當訓練數據集n很大時或者面對高維度數據時,運用CUDA計算架構并行化KNN算法通常可以取得很好的加速效率.
2.2 CUDA編程模型
CUDA是NVIDIA公司推出的一款通用并行計算架構,CUDA架構改變了傳統的GPU編程方式,它不需要將程序任務轉換為GPU圖形處理任務,降低了開發難度.CUDA架構主要包括計算核心和存儲器體系.每個GPU計算核心由多個流多處理器 (stream multiprocessor,SM) 組成,每個SM由多個標量處理器 (stream processor,SP) 組成.同時,GPU提供了可供線程訪問的多級存儲器.每個線程具有私有的本地存儲器,每個線程塊則有共享存儲器,它對塊內所有線程共享數據,并且它的生命周期與塊相同,讀寫速度快.常量存儲器和紋理存儲器是只讀存儲器,可以針對不同的用途進行優化,全局存儲器則用于接收從CPU端傳入的數據.
在CUDA編程模型中,GPU被認為是能夠并行執行大量線程的協處理器.一個簡單的源程序包括運行在CPU上的主機端代碼和運行在GPU上的內核(kernel)代碼.Kernel函數通過__global__類型限定符定義,并通過Kernel<<
3 基于CUDA的KNN算法并行優化
分析串行KNN算法的流程可知,算法的時間開銷大部分都在距離計算階段和排序階段.因此本文著重在這兩個步驟上進行并行優化,并且在GP-U中進行所有計算.以下四個小節詳細介紹了GS_KNN算法的優化過程.
3.1 基于Cublas的距離矩陣計算
Cublas Library是基于NVIDIA的通用函數庫,它實現了Blas(基本線性代數子程序),它允許用戶訪問GPU中的計算單元,在使用時在GPU中分配所需的矩陣向量空間并填充數據,然后調用其中的函數可以加速向量和矩陣等線性運算.對于KNN算法中龐大的距離計算量,本文利用Cublas庫中的矩陣乘法函數cublasSgemm()來加速距離計算,該函數能實現向量與矩陣,矩陣與矩陣之間的運算,并且擁有很好的加速比.
cublasSgemm()函數調用時有許多參數,調用方法為cublasSgemm(handle,transa,transb,m,n,k,*alpha,*A,lda,*B,ldb,*beta,*C,ldc),在Cublas里面所有的矩陣都是按照列優先方式存儲,lda,ldb,ldc代表矩陣A,B,C的行數,矩陣A的維度為m*k,B的維度為k*n,C的維度為m*n,transa和transb代表矩陣A和B是否轉置,函數實現的矩陣運算為:
C=alpha*OP(A)*OP(B)+beta*C
(1)
為了滿足公式(1),GS_KNN算法的距離度量選擇歐幾里得距離的平方.這樣,GS_KNN算法的距離計算可以轉化為:
|x-y|2=x2+y2-2x*y=alpha(x*y)+beta(x2+y2)
(2)
其中,alpha取值為-2,beta取值為1.在設計CUDA核函數時,如果有m個測試數據點和n個訓練數據點,數據維度為d,則矩陣A為x,代表m*d維的測試數據點矩陣,矩陣B為y,代表n*d維的訓練數據點矩陣,由于x和y都是按照列優先方式存儲,實際上在函數運算時矩陣A的維度為d*m,矩陣B的維度為d*n,為了得到m*n維的距離結果矩陣,需要將矩陣A進行轉置,矩陣B不需要轉置,所以將transa這個參數的值設為CUBLAS_OP_T代表轉置,transb這個參數的值設為CUBLAS_OP_N代表不需轉置.由于矩陣A的行數為m,矩陣B的列數為n,矩陣A的列數為d,所以分別將函數參數列表中的m賦值為m,n賦值為n,k賦值為d.在調用函數之前先要計算矩陣C也就是x2+y2的值,對于x2算法開啟m個線程,若矩陣A在CUDA內存中的地址為p,線程編號為threadId,每個線程計算地址在p+d*threadId至p+d*(threadId+1)上的數據平方并求和,即一個測試數據點在d個維度上的平方和.對于y2開啟n個線程,若矩陣B在CUDA內存中的地址為q,線程編號為threadId,每個線程計算地址在q+d*threadId至q+d*(threadId+1)上的數據平方并求和,即一個訓練數據點在d個維度上的平方和.得到以上兩個結果之后,在CUDA中繼續開啟n個線程,每個線程將一個訓練數據點的平方和分別與m個測試數據點的平方和相加從而得到維度為m的向量,則n個線程計算得到m*n維的矩陣,即表達式為x2+y2的輸入的矩陣C.最后將矩陣A,B和C在CUDA全局內存中的地址指針傳入cublasSgemm()函數,函數返回m*n維的距離結果矩陣,每一行向量代表一個測試數據點分別與n個訓練數據點的距離.
3.2 基于k次最小值查找的最近鄰選擇
通過計算獲得每個測試數據點的距離向量后,需要進行排序.雖然有不少研究把排序算法移植到CUDA中執行,如Sintorn等[13]和Satish等[14]的研究,但算法的時間復雜度為O(nlogn),并行度不高.通過分析KNN算法可知,參數k往往遠小于訓練集數據量n,所以對于每一個測試數據來說,沒有必要將它到訓練集的所有距離都進行排序,只需要獲得前k個最小距離即可.冒泡排序算法和選擇排序算法,每次排序都可以選出一個最小值,k次排序就可以獲得k個最小距離.雖然這兩種算法的時間復雜度只有O(kn),但是它們卻無法并行執行,因為每次排序都要依賴前面元素的排序結果.因此,冒泡排序算法和選擇排序算法都不適合CUDA平臺.
本節提出了一個基于k次最小值查找的最近鄰選擇方法,適合GPU的多線程環境,并且是一個基于比較網絡的模型,可以在同一時刻執行多個不相關的比較操作.算法定義的一個比較器如圖2所示,比較器的輸入為兩個任意未經過排序的數據,經過比較器之后兩個輸出被排序,并且上端線路的元素大于或者等于下端線路的元素,一個比較器所執行的時間為一個單位時間,時間復雜度為O(1).

圖2 K次最小值查找的比較器
Fig.2 Comparator of K-min search
對于一個測試數據,經過距離計算之后得到它對n個訓練數據的距離向量{d0,d1,…dn-2,dn-1},需要從該距離向量中選擇出k(k≤n)個最小距離,根據排序網絡的比較器需要兩個輸入,算法將該向量以dn/2處的位置一分為二,然后d0和d0+?n/2」(符號?」表示向下取整)輸入比較器做判斷之后得到max{d0,d0+?n/2」}和min{d0,d0+?n/2」}.與此同時,d1和d1+?n/2」做比較得到max{d1,d1+?n/2」}和min{d1,d1+?n/2」},dn/2之前的一個元素d?n/2」-1和d?n/2」-1+?n/2」比較得到max{d?n/2」-1,d?n/2」-1+?n/2」}和min{d?n/2」-1,d?n/2」-1+?n/2」},當n為奇數時,最后一個數dn-1無須經過比較自動進入下一輪迭代.這些兩兩元素之間的比較是互不相關的,符合CUDA并行執行的特性.在經過第一輪比較器之后會產生兩個子向量l1和l2,如果n為偶數,則向量如下所示:
l1={max{d0,d0+?n/2」},max{d1,d1+?n/2」},…
max{d?n/2」-1,d?n/2」-1+?n/2」}}
(3)
l2={min{d0,d0+?n/2」},min{d1,d1+?n/2」},…
min{d?n/2」-1,d?n/2」-1+?n/2」}}
(4)
如果n為奇數,則子向量l2為:
l2={min{d0,d0+?n/2」},min{d1,d1+?n/2」},…,
min{d?n/2」-1,d?n/2」-1+?n/2」},min{dn-1}}
(5)
產生兩個子向量l1和l2需要經過「n/2?(符號「?表示向上取整)次比較器的使用,在CUDA中這「n/2?次比較可以同時執行,對于要尋找到本輪迭代中的最小值來說,它必定存在于子向量l2中,循環迭代上一步的過程,繼續將向量l2一分為二輸入比較器,直至l2中只存在一個元素時結束迭代,此時最后的這個元素就是本輪迭代中得到的最小值.經過上述的第一輪最小值選擇操作之后,距離向量變為{e0,e1,…en-2,en-1},并且en-1這個元素是該向量中的最小值,也是算法選擇出的第一個最近鄰元素,然后繼續對{e0,e1,…en-2}向量做如上操作,就能得到第二個最近鄰元素.經過k次最小值查找之后,就可以查找出初始距離向量中的k個最近鄰元素,由于每輪迭代中可以在CUDA中開啟多線程并行查找,將原本時間復雜度為O(n)的比較階段降為O(1),所以一次最小值查找的時間復雜度就等于迭代次數O(「log2n?),那么整體k次最小值查找的時間復雜度就是O(k「log2n?),相比于其它排序算法擁有更低的時間復雜度.
綜上所述,基于k次最小值查找的最近鄰選擇算法的詳細步驟如下:
1)將全局存儲器中的m*n的距離矩陣拷貝至共享內存.
2)當n的值小于1024時,在CUDA中開啟m個線程塊,每一個線程塊負責一個測試數據點距離向量的排序,每個線程塊內部分配「n/2?個線程,每個線程負責兩個對應位置上數據的比較器選擇,留下值較小的數據并更新到共享內存上.
3)每一輪迭代通過syncthreads()函數同步塊內的所有線程,同步完成之后繼續對子向量l2進行比較器選擇,在完成O(「log2n?)次迭代之后,每個線程塊零號線程對應位置上的共享內存存儲的數據就是本輪最小值.
4)經過k次選擇就得到屬于該測試數據的k個最近鄰.
當n的值較大時,由于CUDA架構的硬件限制,則每個向量需要使用「n/1024?個線程塊負責計算,通過找出這些線程塊輸出數據中的最小值從而得到最近鄰數據.
3.3 基于雙調排序的最近鄰選擇
通知分析可知:基于k次最小值查找的最近鄰選擇算法,當k值比較大時,經過k次查找所需要的時間也越大.從時間復雜度上分析,如果k值接近于訓練集數據量n時,該方法的時間復雜度就變為O(nlogn),與快速排序的時間復雜度相同,相當于將距離向量完全排序,因此它不適應k值較大的情況.本節介紹了一種基于CUDA的雙調排序算法,它同樣能夠利用多線程特性來并行執行,適合于k值比較大的排序場合.
本算法定義一個序列s=(a0,a1,…,an-1),如果滿足條件a0≤a1≤…≤an/2-1并且an/2≥an/2+1≥…≥an-1,那么稱序列s就是一個雙調序列.算法將任意一個長度為n(n為偶數)的雙調序列s分為相等長度的兩段s1和s2,將s1中的元素和s2中的元素一一比較,即a[i]和a[i+n/2](i 經過距離計算得到的m*n的距離矩陣,使用基于雙調排序的最近鄰選擇算法的詳細步驟如下: 1)對于每一個測試數據對應的距離向量l,其長度為n,算法中雙調排序輸入的序列長度為2a(a>0),當n的大小不足2a時,補足最少個數的元素使n=2a,補足的元素統一為能夠表示的最大數. 2)將數據拷貝至共享內存,同時開啟若干個線程塊負責距離序列的雙調排序,塊內總共進行a輪迭代,前a-1輪進行相鄰兩個單調性相反的序列合并,并分別按相反單調性遞歸進行雙調排序. 3)第a輪時合并前面兩個長度為n/2的單調序列,開啟n/2個線程做兩兩元素的比較,按此方式迭代a輪,每輪都會開啟n/2個線程參與計算,直至最后一輪迭代時是長度為2的序列相比較,即可得出最后單調遞增的距離序列. 圖3 構建雙調序列示意圖Fig.3 Diagram of a bitonic sequence 基于雙調排序的最近鄰選擇算法的時間復雜度為O((logn)2),所以當k較大時,該方法的時間復雜度是優于基于k次最小值查找的最近鄰選擇算法. 基于CUDA的決定分類標號的具體步驟如下:在CUDA中開啟m個線程塊,每個線程塊負責一個測試數據分類標號的統計,在共享內存上開辟一個數組,數組長度為訓練數據集的類別個數.塊內開啟k個線程,每個線程統計自己對應位置上數據的類別標號,采用CUDA內部的原子加法操作統計,即atomicAdd()操作,在類別數組上取數據并執行加法操作.最后同步線程塊內線程,得到最終記錄數組,數組當中數字最大的類別即為該測試集最終的分類. 綜合前面各節所述,GS_KNN算法的詳細步驟如算法2所示,算法流程如圖4所示. 圖4 GS_KNN算法流程圖Fig.4 Flow chart of GS_KNN algorithm 算法2.基于CUDA的GS_KNN算法 輸入:m個點的測試數據集,n個點的訓練數據集,以及最近鄰個數k. 輸出:m個測試數據的分類結果 1)在CPU主機端初始化測試數據集,訓練數據集和最近鄰個數k的內存空間. 2)在GPU設備端分配測試數據集,訓練數據集以及最近鄰個數k的內存空間. 3)將主機端數據拷貝至設備端. 4)利用CUDA調用基于Cublas通用矩陣乘的距離計算內核函數,得到所有測試數據集數據到訓練數據集的距離矩陣. 5)隨機抽取一個測試數據的距離向量,分別進行基于k次最小值查找和基于雙調排序的最近鄰選擇排序算法的實驗,得到時間T1和T2. 6)如果T1小于T2,則選擇基于k次最小值查找的最近鄰選擇算法,進行距離排序.否則,選擇基于雙調排序的最近鄰選擇算法來排序. 7)進行基于CUDA的決定分類標號,得到每個測試數據的分類結果. 8)將最后的分類結果從GPU設備端返回拷貝至CPU主機端并輸出. 本文所使用的實驗平臺為Intel Core i5-4590 CPU,主頻3.30GHz,內存8GB,GPU為NVIDIA GTX750 Ti,計算能力為5.0,擁有5個流多處理器,640個SP.軟件環境為Windows 10,Visual studio 2010和CUDA7.0. 本文實驗所使用的第一個數據集為程序生成的模擬數據,可以指定測試集大小、訓練集大小、每個樣本的類別以及它的屬性維度.第二個數據集為KDDCUP1999提供的網絡入侵檢測數據集,該數據集包含大量真實的網絡入侵數據,數據集中每個元素包含41個維度的屬性,每個維度屬性為浮點類型的數據,總共有24種攻擊類型.由于每個維度上的度量單位不同,需要對輸入數據進行標準化和歸一化,本文使用Wang等[15]的方法進行數據的預處理. 4.2.1 固定m,k,改變n,d對加速的影響 本實驗采用模擬數據,設定測試集的大小m為1200,訓練集n的大小為210到215,這樣可以方便線程的訪問,測試集與訓練集的維度d相同,k的值設為25.由于k值較小,所以經過評估后算法采用基于k次最小值查找的最近鄰選擇.選擇了兩種算法來與GS_KNN算法作對比.第一種算法選用了基于CPU的超快近似最近鄰搜索算法庫,即ANN-C++[16],另一種選用了BF-CUDA算法.改變n和d的大小,實驗結果如表1所示,可以看出GS_KNN算法在相同數據集上的性能上要優于ANN-C++算法和BF-CUDA算法,并且隨著訓練集大小和維度的增加,GS_KNN算法相較于這兩個算法的加速比也越來越高,當n等于215,d等于256時,GS_KNN算法相對于ANN-C++算法的加速比為145,相對于BF-CUDA算法的加速比為2.8. 4.2.2 固定m,n,d,改變k對排序的影響 實驗(1)是在固定k=25的情況下進行的,為了比較k值的大小對算法距離排序階段的影響,選取測試數據集大小為1200,測試數據集為16384,數據維度為32,第一次實驗中GS_KNN算法的距離排序采用基于k次最小值查找的最近鄰選擇,第二次采用基于雙調排序的最近鄰選擇,然后每次實驗都不斷增加k的值,觀察記錄距離排序階段的執行時間,實驗結果如圖5所示,可以看出當k的值為46時,基于雙調排序和基于k次最小值查找的距離排序所用時間相同,當k的值小于46時,k次最小值查找所需的時間要少于雙調排序.隨著k的不斷增加,雙調排序所花費的時間不變,因為不管k值如何變化,算法都會得到一個完整的排序結果,而k次最小值查找的時間開銷呈線性增長趨勢,因為算法的迭代次數會隨著k的增加而線性增加,此時雙調排序的優勢會越來越明顯. 表1 改變n和d時各算法運行時間比較(單位:s)Table 1 Comparison of running time of each algorithm when changing n and d (unit:s) 圖5 改變k對距離排序時間的影響Fig.5 Effect of changing k on distance sorting time 4.2.3 算法準確性驗證 從KDDCUP99數據集中選取5000條數據,其中4900條正常數據,100條包含攻擊的入侵數據作為訓練集,再選500條包含正常數據以及訓練集中未知的入侵數據集作為測試集,分別運用經典的基于CPU的K最近鄰入侵檢測算法和GS_KNN算法,進行10次實驗取檢測率和誤報率的平均值,每次調整k值的大小,統計結果如表2所示. 表2 入侵檢測魯棒性檢測結果Table 2 Intrusion detection robustness test results 從結果來看,GS_KNN算法在檢測4類攻擊上與標準CPU版本的K最近鄰算法相比,檢測率和誤報率幾乎相同.造成略微差異的主要是由于在距離排序階段,離測試數據距離完全相等而類別標號不同的訓練數據被k的不同切分所導致. 本文在經典串行KNN算法的基礎上,利用GPU的并行計算能力,提出了一種基于CUDA的并行KNN算法,即GS_KNN算法,該算法能有效處理大規模數據情況下的數據分類問題.算法利用矩陣乘的思想加速了距離矩陣的運算,提出基于k次最小值查找和雙調排序兩種策略優化距離排序,并在CUDA中完成分類標號的統計.它與經典的BF-CUDA算法相比獲得2.8倍的加速比.然而本文在GPU和CPU之間的數據傳輸以及多GPU協同合作還有待研究,因此下一步盡可能優化數據的存儲,利用GPU集群提升算法的性能.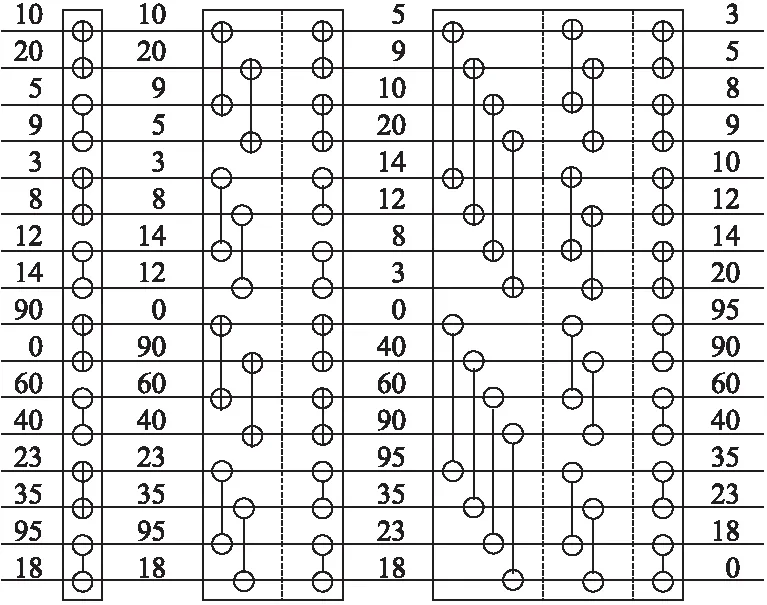
3.4 基于CUDA的決定分類標號
3.5 GS_KNN算法的詳細步驟

4 實驗與分析
4.1 實驗環境
4.2 實驗結果

5 結 論

