基于差分進化和森林優化混合的特征選擇

林達坤，黃世國，林燕紅，洪銘淋

1(福建農林大學 智慧農林褔建省高校重點實驗室，福州 350002)2(生態公益林重大有害生物防控福建省高校重點實驗室，福州 350002)

1 引 言

特征選擇在機器學習中扮演重要角色.通過特征選擇可以提高模型預測精度、減少計算時間.但選擇最優特征子集是一個NP-hard問題.當特征的數量為n時，其特征子集的數量為2n.應用窮舉方法評價每個特征子集的效果將產生大量計算，現有計算能力一般難以滿足計算需求.因此，許多學者提出眾多特征選擇算法旨在尋找近似最優解.特征選擇方法一般分為嵌入式、過濾式和封裝式.過濾式特征選擇只考慮數據集的內在性質，在選擇過程中不考慮目標評價問題.封裝式特征選擇通過評價不同特征子集尋找近似最優的集合.嵌入式特征選擇則是將特征選擇作為組成部分嵌入到學習算法.由于封裝式特征選擇一般比過濾式特征選擇具有更優的評價結果[1]，因此，基于元啟發機制的特征選擇方法一般采用封裝式特征選擇.

與傳統特征選擇方法(如序列向前算法和序列向后算法)易陷入局部最優相比[2]，基于元啟發機制的算法，特別是群智能計算方法由于其很強的全局搜索能力，在特征選擇中得到廣泛研究.目前，許多群體智能優化算法都已被成功應用到特征選擇中.Babatunde等[3]在2014年提出一種基于二進制遺傳算法的特征選擇，結果表明該算法能夠有效剔除無用特征并提高分類精度.但遺傳算法的局部搜索能力較差，在進化后期搜索效率較低.Kennedy和Eberhart在1997年提出粒子群優化(Particle swarm optimization，PSO)的二進制版本[4].Emary等在2015年提出二進制灰狼優化(Binary grey wolf optimization，BGWO)，結果表明該算法能夠在特征空間中搜索到合適的特征組合[5].但該算法存在著收斂速度快，易早熟等缺點.Mirjalili在2015年提出基于蜻蜓算法(Dragonfly algorithm，DA)的特征選擇[6].該算法在特征選擇過程中也存在早熟、求解精度不高等問題.Ghaemi等在2014年提出森林優化算法(Forest optimization algorithm，FOA)[7]，在2015年將其應用于特征選擇中，結果表明森林優化算法具有較好的性能[8].但該算法的局部搜索方式趨向于窮舉式搜索，存在著計算量大、收斂速度慢等問題.

由于各種群體智能優化算法有其優點也有不足，采用單一的算法有時難以獲得滿意的效果.近年來，一些學者綜合多種群智能優化算法的優缺點，將其混合用于特征選擇，取得了較好的效果.李虹等將遺傳算法與粒子群優化算法結合，提出了混合粒子群優化算法，結果表明該算法具有較強的全局搜索能力，能夠有效避免粒子群優化算法早熟收斂的問題[9].Khushaba等將蟻群算法與差分進化算法結合，進一步提升了蟻群算法的開發與探索能力，實驗結果表明該算法能夠取得較高的分類精度[10].Zawbaa等將灰狼優化算法與蟻獅優化算法結合，且將其用于小樣本高維數據集的特征選擇，結果表明該算法具有良好的降維效果與分類精度[11].

本研究針對森林優化算法收斂速度慢的問題，采用智能算法混合策略，提出基于差分進化和森林優化混合的特征選擇.利用差分進化算法較快收斂的特點，在森林優化算法前期引入差分進化算法使其加快收斂.同時，針對森林優化算法局部搜索計算量大的問題，利用局部搜索中每棵樹的取值僅改變一位的特點，給出了更有效的距離計算方法，進一步提高了算法的性能.

2 基于森林優化算法的特征選擇

特征選擇是指從已有的M個特征中選擇N個特征使得系統的特定指標最優化.針對分類問題的特征選擇，通常是產生一條二進制編碼.“1”代表選擇相應特征，“0”代表去除相應特征.

森林優化算法是模擬利用種子傳播找到生存條件優越的棲息地來搜索問題的最優解.一棵樹代表問題的一個可能解，由所有樹構成的森林則代表問題所有解.該算法有5個步驟：初始化森林、局部播種、種群限制、全局播種、更新最優樹.具體步驟如下.

Step1.初始化森林：產生n棵樹，每棵樹都以一維數組[v1,v2，…，vD,Age,Fitness]表示，其中D為問題的維數，變量V的取值為1或0，Age代表樹的年齡，其初始值為0，Fitness為適應度值(評價樹的好壞).

Step2.局部播種(Local seeding)：每棵年齡為0的樹產生LSC棵與父代完全相同的樹，然后隨機選中每棵新樹的某一維(不包括Age與Fitness)，將其值取反.將森林中的老樹的年齡加1且新樹的年齡設為0.

Step3.種群限制：森林中當樹的年齡大于最大年齡數(Life time)將該樹從森林中剔除并放入候選種群.當森林中保留下來的樹的數量超過區域限制時，則剔除適應度值較差的樹并將其也放入候選種群.

Step4.全局播種：從候選種群中隨機選出一定數量的樹.對每棵被選中的樹隨機選中GSC維，將其值取反.

Step5.更新最優樹：將森林中適應度值最大的樹作為最優樹，并將該樹的年齡設為0，以便于最優樹能在下次迭代中進行局部播種.

3 基于差分進化和森林優化混合的特征選擇

具有反饋機制的二進制差分進化(Binary Differential Evolution with Feedback Strategy，BFDE)[12]是二進制差分進化算法的變種，能獲得更好的降維和分類效果.森林優化算法中的局部播種方式是一種精細搜索方法，計算量大，算法收斂速度慢，同時，差分進化具有較快的收斂速度，因此本研究在森林優化算法早期迭代階段利用BFDE算法進行特征選擇，后期則繼續利用森林優化算法進行特征選擇，以充分發揮森林優化算法局部搜索的優勢.我們提出的新算法命名為差分進化和森林優化混合的算法(Differential Evolution Based Forest Optimization Algorithm，DEFOA).

3.1 具有反饋機制的二進制差分進化

BFDE的具體步驟如下：

(1)

S(xi,j,t)=1/(1+e-xi,j,t)

(2)

BFDE的變異操作方式為DE/current-to-best/1，具體操作如公式(3)所示.

(3)

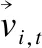
算法 1.

輸入：種群大小N，最大迭代次數T.

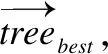
2.評價二進制種群Pbt.

fori=1 to N

利用公式(4)、(6)對種群Pt進行交叉變異操作產生新向量Gi,t，同時將界限控制在[xmin,xmax]之間.

End fori

利用公式(1)、(2)更新并評價二進制種群Pbt.

利用公式(5)進行反饋操作.

End for t

4.將二進制種群Pbt的每個個體xbi,t看作森林優化算法中的樹，額外增加一維Age，Age初始值全為0.

fori=1 to N

對Age為0的xbi,t進行局部播種產生LSC棵Age為0的新樹，xbi,t老化Age值加1.

評價每棵新樹.

End fori

進行種群限制，清除前次迭代產生的候選種群，形成新的候選種群.

利用公式(7)、(8)對候選種群進行反饋調節.

對候選種群進行全局播種，評價新樹并加入到二進制種群Pbt中.

為維持種群大小N，再次進行種群限制.

更新最優樹.

End for t

(4)

BFDE在原有差分進化的基礎上引入了反饋操作，利用公式(5)將二進制種群Pbt的信息反饋到原始種群Pt中.

(5)

3.2 差分進化和森林優化混合的特征選擇

(6)

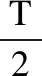
(7)

(8)

i=1，…，N，j=1，…，D.DEFOA的偽代碼如算法1所示.

3.3 針對局部搜索階段改進的K最近鄰算法

在基于智能計算的封裝式特征選擇算法的更新迭代過程中，每更新產生一個新粒子需要對其進行評價.該評價過程計算量大，增加了算法的計算時間.特別是在DEFOA和FSFOA[8]的局部播種階段會產生大量相似的粒子(新樹與老樹只有一維不同).若為了評價這些相似粒子，均利用分類算法重新訓練，必將顯著增加算法的計算量.

針對局部播種階段這一特殊情況，本研究引入一種改進的K最近鄰算法(K Nearest Neighbor,KNN)[13]，以降低DEFOA算法的計算量，提高運行速度.該KNN用于森林優化時作如下改進：1)在局部播種時，Age為0的樹所對應的樣本距離被保留.2)評價新樹時，只需計算值發生改變的維數所對應的樣本距離.

改進的KNN的優點在于老樹進行局部播種時無需重新計算新樹所對應樣本總距離，只需計算值發生改變的一維所對應樣本距離與老樹相加減即可，大大地減少了原本的計算量.

4 實驗與結果

4.1 數據集

為了評價DEFOA的性能，使用不同的數據集進行實驗.所使用數據集的具體信息如表1所示，共10個數據集.除SRBCT來自http：//www.gems-system.org.外，其它數據集均來自UCI machine learning repository(http：//archive.ics.uci.edu/ml/datasets.html).其中，Wine、Zoo、Dermatology的特征維度較低，Sonar、Movement、HilVally_noisetrain屬于中維度數據集，Musk1、Arrhythmia、LSVT和 SRBCT屬于高維度數據集.

表1 數據集Table 1 Datasets

4.2 參數設置

為了評估DEFOA的性能，DEFOA和現有的特征選擇方法進行比較.本研究主要選擇了6種算法：BFDE、FSFOA、BGWO、GA、BPSO和BDA.實驗采用的是K作為分類器，K值設為5.10折交叉驗證的分類錯誤率的平均值AE將作為適應度值，具體計算過程如公式(9)、公式(10)所示.

(9)

(10)

所有算法由美國MathWorks公司出品的MATLAB(R2014b)編程實現.所有實驗均在3.6 GHz CPU和8GB RAM的Intel Core i5機器上獨立運行10次.所有算法的迭代次數設為100，種群大小為50.在DEFOA中，F值設為0.9，CR值設為0.6.對于DEFOA與FSFOA的共有參數，“Life time”為15，“Transfer rate”為5%，LSC與GSC依賴于問題的維數，一般LSC為數據集維數的20%，GSC為數據集維數的40%.GA的交叉概率為0.8，變異概率為0.1.BPSO的學習因子c1和c2值都為2，其慣性權重區間為[0.4，0.9].

為進一步提升所有算法的性能，在進行實驗前對數據集進行0-1標準化.具體如公式(11)所示，其中X代表原始變量值，X*代表標準化后的變量值，max是變量的最大值，min是變量的最小值.

(11)

4.3 結果與分析

圖1表明FSFOA與DEFOA使用改進的KNN作為分類器后的運行時間減少率，易看出改進的KNN能夠顯著降低算法的運行時間.這也進一步證明引進的KNN能夠有效解決森林優化算法局部播種計算量大的問題.

表2展示了DEFOA與其它算法的分類性能對比結果.Mean代表算法獨立運行10次結果的平均值，Std代表其標準差.Rank是對算法在不同數據集上的性能對比排序結果，Mean值越小則排名越前，若Mean值相同，則Std值小的排前.從表2可看出DEFOA除在數據集Wine的排名在第2位外，其它數據集排名均在第1位，且其對應的標準差相對較小，說明DEFOA的分類性能較為穩定.Average Rank是對算法在不同數據集上排序值總和的平均值，根據Average Rank可得出每個算法的總排名.從表2易得出DEFOA的分類性能比其他6種算法好.

圖1 新型KNN的計算效率Fig.1 Computational efficiency of new KNN

表2 算法分類性能對比Table 2 Comparison of classification performance in algorithms

為進一步驗證DEFOA對分類性能的影響，將DEFOA與其它特征選擇算法進行t檢驗，結果如表3所示.其中“+”表示DEFOA性能顯著大于其它算法，“=”表示兩者相似.易看出DEFOA除在數據集Wine、Zoo、Dermatology上與其它特征算法性能相似外，在其它數據集上的性能皆顯著高于其它算法.因此，DEFOA在中維度和高維度數據集上具有良好的分類性能.

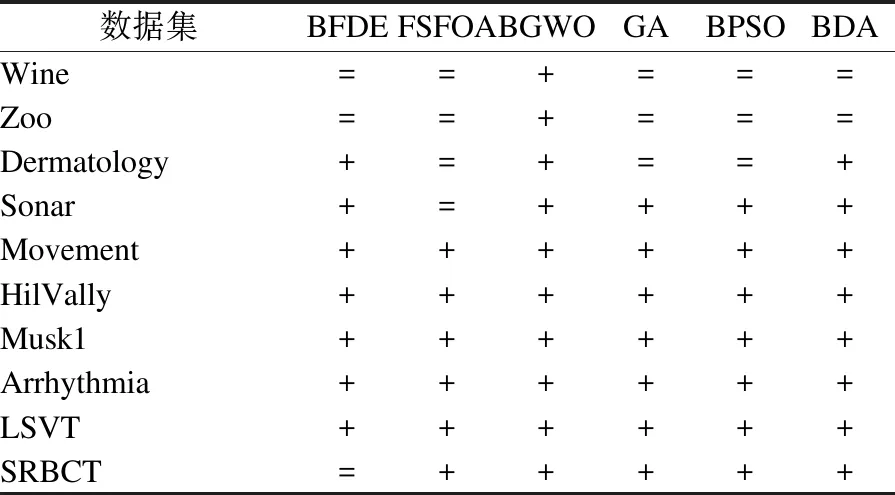
表3 DEFOA分類性能的t檢驗Table 3 T test for classification performance of DEFOA

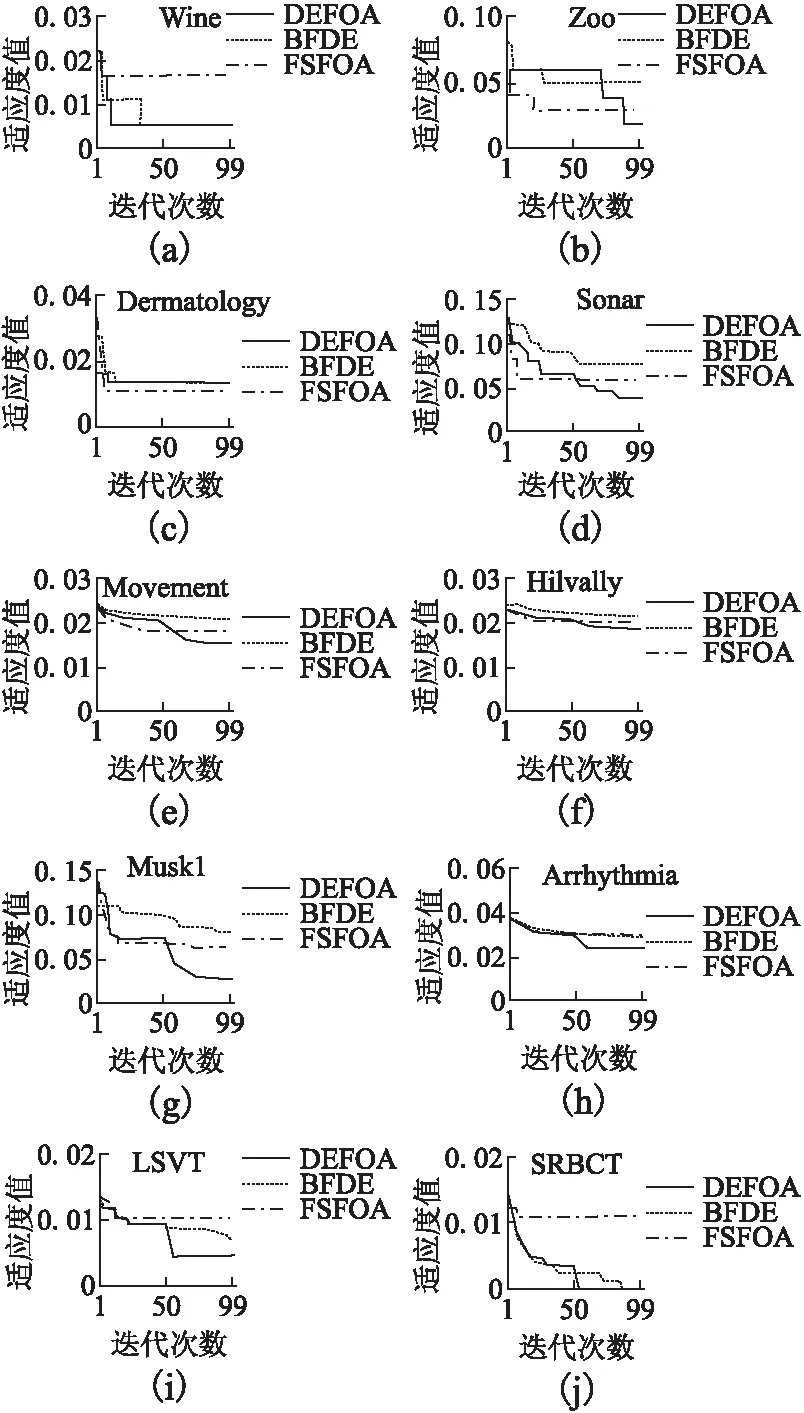
圖2 算法收斂圖Fig.2 Convergence diagram of algorithms

圖2是不同算法在不同數據集上的收斂圖.易看出DEFOA在各數據集上均能獲得較好適應度值且具有更穩定的收斂速度.

5 結 語

本研究針對森林優化算法的局部播種計算量過大的問題，在森林優化算法的前期迭代中使用差分進化算法代替局部播種，提出差分進化和森林優化混合的算法.經實驗驗證，該算法具有良好的分類性能與穩定的收斂速度.此外，還引入一種改進的KNN代替傳統的KNN作為分類器，實驗結果表明改進的K最近鄰算法能極大降低所提出的混合算法與森林優化算法的運行時間.