隨機森林和水平集的椎骨CT分割方法
陶永鵬,景 雨,頊 聰
(大連外國語大學 軟件學院,遼寧 大連 116044)
1 概 述
脊柱,是人體中央負重骨骼,是人體上半身結構的中軸線.新型掃描技術中CT是評估三維空間椎骨形態最精確的方式.椎骨CT圖像分割是診斷的基本步驟和任務,如識別脊椎異常診斷[1],生物力學建模或圖像引導脊柱干預[2].為了保證分割的準確性,圖像引導脊柱干預等通常需要亞毫米級精度.但由于椎骨形狀的復雜性和結構的變化性等特點,傳統的圖像分割方法并不適用于椎骨的分割.
近年來,眾多學者已提出部分針對椎骨圖像的分割算法.一些無監督的圖像處理方法也被應用于椎骨的分割,流域[3]和圖形[4]等處理復雜拓撲結構的水平集方法被應用于椎骨分割.Lim等[5]將Willmore流程納入水平集框架來擬合表面模型的演變.黃等[6]結合邊緣和基于區域的水平集函數實現CT圖像中椎體的分割.李等[7]提出了一種自動初始化水平集方法,實現基于混合形態濾波和高斯混合模型處理拓撲變化.Klinder等[8]提出了集成檢測框架,基于脊柱曲線提取和統計形狀模型識別和分割椎骨.Roberts等[9]使用主動形狀模型將椎骨分成幾部分進行分割協作,可應用于二維射線圖像并可以擴展到三維.唐利明[10]等提出了變分水平集的分割模型提高了對噪聲圖像的分割能力,但受聚類數目的影響較大.這些模型在某種程度上達到了較高的分割準確度,但初始姿態較敏感,部分并且需要對圖像手動改動.
目前,機器學習技術已被應用于醫學CT圖像.簡[11]等使用隨機森林分類算法成功的從存在背景干擾和光照變化的圖像中實現了目標檢測,但該方法并不能確定器官的范圍.Pauly等[12]應用隨機蕨類(random ferns),同時引入 3DLBP(Local Binary Patterns)特征,實現了對 MR 圖像中多重解剖結構位置和大小估計.Glocker[13]采用一種有向距離圖譜對人體器官進行檢測,將有向距離圖譜作為目標邊界形狀的隱式表達,通過邊界內外體素的正負值進行檢測.
2 本文方法
本文針對椎骨圖像分割中對初始輪廓敏感的問題,提出基于加權隨機森林和水平集分割的椎骨CT分割方法.提取CT圖像的SIFT特征,通過隨機森林分類回歸算法選擇距離圖譜中距離值最小的100個點進行Mean-shift 聚類分析,產生聚類中心,重建操作后獲得對應的3D距離預測圖譜,選取距離最小的點作為隨機森林確定的椎骨中心點.隨后將獲得的椎骨中心點作為CV分割模型的初始輪廓位置,通過求解平穩控制演化速度和噪聲敏感度的CV模型,由能量函數演化方程最小值來實現對椎骨CT圖像的分割.方法示意圖如圖1所示.
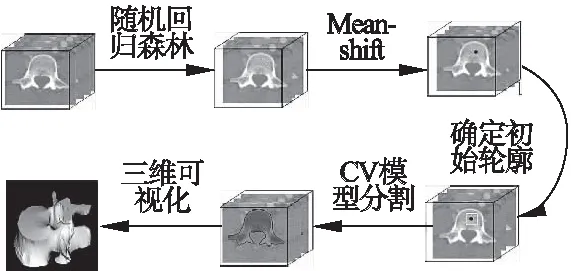
圖1 方法示意圖Fig.1 Schematic of the method
3 SIFT特征
SIFT特征(Scale-invariant feature transform)是一種圖像局部特征提取算法,能夠保持較好的穩定性.在描述子的生成過程中,對于16×16的關鍵點鄰域,在處理梯度時進行高斯加權處理,強化中心區域,淡化邊緣區域的影響.在每個4×4 子區域上計算8個方向的梯度方向直方圖,即形成一個種子點,每個關鍵點描述子由4×4=16個種子點組成,每個種子點有8個梯度方向信息,形成4×4×8=128維的SIFT特征向量.
4 隨機森林
本文方法將訓練數據點定義為Dk=(Sk,Ck),其中Sk是基于體素k得到的SIFT特征向量,Ck是體素k到標記椎骨中心點i的距離.概率密度函數為p(Ck|Sk).隨機森林回歸目標函數I(Dj,θ)定義為:
(1)
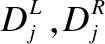
本文采用連續形式的微分熵:
(2)
樣本數據點D,采用連續高斯模型密度分布p(Ck),并將b元高斯的微分熵函數定義為:
(3)
根據一維輸入與輸出的回增益表達式推導過程[14],推廣到多元變量的情況可得:
(4)
其中,Λy為條件協方差矩陣,可以得到一棵決策樹的后驗概率pt(Ck|Sk),對T棵樹的后驗概率求平均值,T為決策樹數量,并將后驗概率平均值作為回歸的結果.
(5)
因為決策樹之間的決策結果差異較大,隨機森林中決策樹的性能越好的決策樹應該占有更高的比重.為解決這個問題,對隨機森林中的決策樹采取加權運算,來提高準確率.每棵決策樹的可信度可由公式(5)計算得到的后驗概率表示.
隨機森林初始化時,所有樹的權值相同,為:
ω0(k)=1/T
(6)
本文提出隨機回歸森權重公式為:
(7)
其中,ω(k)表示分類森林中第k棵決策樹的權重,γ(k)為第k棵決策樹的回歸中心與專家標記點間的距離,γ(k)越大所占權重越小,通過迭代優化最小絕對誤差函數來訓練隨機回歸森林.

4.1 水平集演化分割
由于水平集分割模型對初始輪廓敏感且脊柱CT圖像的灰度不均勻分布,可能會導致陷入局部最小,分割不完全.為了減小誤差,將初始輪廓置于隨機森林定位的椎骨中心點上并設定曲線由內向外演化.
令I為區域Ω上的一幅椎骨CT圖像,將分割的初始輪廓L選取在隨機森林算法確定的椎骨中心點位置,并使用水平集分割算法對椎骨CT進行分割,設定輪廓由內向外膨脹.
將邊緣指示函數定義為:
(8)
其中Gσ是標準方差為σ的高斯核函數,像素為D(x,y).引用兩個參數來調整水平集演化的速度及噪聲敏感度,β>0,γ>0,其中β用來調整演化速度,γ用來控制噪聲敏感度.
引進參數后,將新的水平集能量方程定義如公式(9).
E(φ)=αRp(φ)+λLl(φ)+ηAl(φ)
(9)
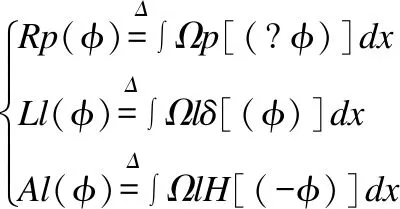
(10)
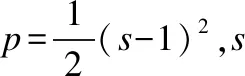
使用梯度下降法將公式(7)的能量方程進行最小化求解得到水平集演化方程如公式(11):

(11)
通過逆向有限差分算法,可得:
(12)
根據公式(10)進行水平集函數φ的演化,直至演化曲線達到穩定狀態后停止演化.為使分割更為準確,對達到穩定狀態的停止演化的曲線進行平滑曲線操作,作為最終的分割輸出結果,完成椎骨CT圖像分割.
本文方法實現椎骨CT圖像分割步驟如圖2所示.

圖2 分割步驟Fig.2 Segmentation step
4.2 分割結果
本文使用公開的椎骨CT分割挑戰數據集,對數據集中提供的20組脊柱CT圖像共計1190張CT圖像進行分割實驗.實驗環境為Intel Pentium 3.2 GHz CPU、4GHz GPU、MATLAB R2010a.實驗結果如圖3所示.
在圖3 (a)為初始輪廓椎骨CT的分割結果;圖3(b)為椎骨中心點位置,其中黑色點為最終確定椎骨中心點,周圍淺色區域為待定中心點;圖3(c)輪廓分割初始輪廓選取結果,其中白色方框為初始輪廓;圖3(d)本文方法椎骨分割結果,深色區域為本文方法分割結果,白色區域為專家手動分割真實值;圖3(e)為整個胸椎和腰椎的分割結果圖.
本文方法對椎骨可以準確、穩定地分割,相比其他算法對于任意位置初始輪廓的分割結果,準確性具有很大的提高.為了能夠更直觀的觀察椎體的分割效果,對腰椎椎骨L3、L4、L5的分割結果進行了三維重建,如圖4所示.
根據骰子系數(DC),對本文方法進行評估和對比,其定義如下:
(13)

圖3 椎骨切片分割結果Fig.3 Vertebral slice segmentation result
其中,Sr是參考體積,Ss是分割體積.將脊柱分為三段(T1-T6,T7-T12和L1-L5)對分割的平均骰子系數進行計算,本文方法分割結果骰子系數平均為0.936,具體結果如表1所示,隨機抽取4組脊柱CT進行了分割結果的骰子系數統計,結果如圖5所示.

圖4 腰椎分割結果三維可視化Fig.4 3D visualization results of lumbar segmentation

T1-T6T7-T12L1-L5All骰子系數0.9250.9320.9510.936
表2對本文方法的椎骨分割結果與其他3個算法進行了詳細比較.方法1只分割了腰椎區域,不能分割胸椎區域;方法1和方法2需要對椎骨進行手動定位;方法3和本文方法能夠對椎骨自動定位,本文方法分割更準確.本文方法分割骰子系數平均為0.936,能夠自動定位中心位置并有較高的分割準確率.
表2 椎骨CT分割結果對比
Table 2 Comparison of CT segmentation results of vertebrae

方法椎骨定位分割方法骰子系數DC方法1[15]手動定位統計形狀模型0.930方法2[16]手動定位平均形狀模型0.934方法3[17]自動定位平均形狀模型0.930本文方法 自動定位WRF-CV 模型0.936

圖5 測試CT集分割結果Fig.5 Test CT set segmentation results
5 結束語
本文提出了基于加權隨機森林和CV模型的椎骨CT圖像分割方法.通過對不同數據進行實驗得出,本文提出的算法能夠成功定位椎骨中心位置,能夠有效解決因初始輪廓不正確而造成的過分割和分割不完全的問題,在自動定位和準確性方面具有一定的優勢.在之后的研究學習中,還需要研究更為通用的椎骨CT圖像分割方法,提高自適應性.

