林區貨車ABS滑模控制器優化設計

楊云杰　朱洪前　馮磊華

摘要：由于林區道路濕滑、路面狀況復雜，采用傳統控制方法的防抱制動系統存在響應速度慢、魯棒性差等問題，制動效果不理想，為此本文提出RBF神經網絡與滑模變結構相結合的控制方法，建立貨車在林區制動情況的分析模型。實驗結果顯示：與常規滑模變結構控制相比，采用基于RBF滑模變結構控制的系統制動時間減少約0.185 s，制動距離縮短約1.88 m，到達最優滑移率和最大制動力矩的時間更快，系統更穩定。因此該方法不僅能夠削弱常規滑模變結構控制所引起的抖振現象，而且能夠提高ABS的響應速度和魯棒性，能夠很好地適應林區濕滑、復雜的路面狀況，從而驗證了所設計模型在實際應用中的可行性和有效性。

關鍵詞：防抱制動系統;徑向基函數;神經網絡;滑模變結構控制;抖振

中圖分類號：U463文獻標識碼：A文章編號：1006-8023（2019）02-0055-06

Optimization Design of ABS Sliding Mode Controller?for Trucks in Forest Area

YANG Yunjie?1， ZHU Hongqian?1*， FENG Leihua?2

（1. College of Materials Science and Engineering， Central South University of Forestry and Technology， Changsha 410004;?2. College of Energy and Power Engineering， Changsha University of Science and Technology， Changsha 410004）

Abstract：Due to the slippery roads in the forest area and the complicated road conditions， the anti-lock braking system using the traditional control method has problems such as slow response speed， poor robustness， and poor braking effect. In this paper， the control method combining RBF neural network and sliding mode variable structure is proposed， and the analysis model of truck braking condition in forest area is established. The experimental results show that compared with the conventional sliding mode variable structure control， the system braking time based on RBF sliding mode variable structure control is reduced by 0.185 seconds， and the braking distance is shortened by 1.88 meters. The time to reach the optimal slip ratio and the maximum braking torque is faster and the system is more stable. Therefore， the method can not only weaken the chattering phenomenon caused by the conventional sliding mode variable structure control， but also improve the response speed and robustness of the ABS， and can well adapt to the wet and complex road conditions in the forest area. The feasibility and effectiveness of the designed model in practical applications are verified.

Keywords：Anti-lock braking system; radial basis function; neural network; sliding mode variable structure control; chattering

0引言

汽車防抱制動系統簡稱ABS系統，作用就是在汽車制動時，根據車輪轉速自動管內壓力的大小，讓車輪處于邊抱死邊滾動的滑移狀態，縮短制動距離，使方向保持良好穩定性的一種安全裝置?[1]。ABS系統的作用決定了它必須具有較強的魯棒性、實時性和抗干擾能力。目前，汽車防抱制動系統的控制方法有多種，其中主要的控制方式有：邏輯門限控制、PID控制、模糊控制、滑模控制和神經網絡等?[2]。

當前國內外的ABS系統大多采用邏輯門限值控制方法?[3-4]。邏輯門限值控制算法雖然簡單，但是需要大量實驗獲得，對本文所研究的林區復雜路面的適應性差，控制效果不是特別理想。以滑移率為控制目標，更容易實現不間斷控制，提高制動過程的平穩性。實現連續控制最簡單的算法就是PID控制?[5]，但由于控制過程具有非線性、時變性和不確定性，PID算法也難以實現。滑模變結構控制作為一種非線性控制方法，能夠很好的滿足本文所需的要求?[6]，但是由于滑模控制器非線性特點使得系統控制信號會產生抖振，高頻抖振還有可能激勵起系統中固有振蕩源，對系統造成更大地影響?[7]。

公式（8）、（10）、（11）代入公式（12）可得制動執行器的數學模型：

Tb=k·Ik-Tm

（13）

其中，

k=9.55·2?π?·Ke·i·ηX·ηS·Kp·/Ph，

Tm=kp·Nm。

2基于RBF滑模控制器的設計

單輪車輛數學模型（1）可寫為：

=RFf-Tb/J?v=-Ff/m。（14）

結合公式（13），上式整理為：

=μBτb-τiueq+τm?v=-μBg。 （15）

其中，τb=RFn/J，τi=k?/J，τm=Tm，ueq=Ik。

公式（2）對時間求導得：

λ=-Rv+Rωv?2v。（16）

定義滑模面為：

Sλ，t=?d?s?d?t+δ?n-1e。（17）

這里，e=λ0-λ（λ0為道路最佳滑移率，λ為實際滑移率），δ為待設計正常數（一階系統中δ不做討論）?[19-20]。

在一階系統中n=1，因此?[19]：

S=e=λ0-λ。（18）

當系統在理想狀態下沿著滑模面滑動時：?S?=0，求導得：

S=-λ=0。（19）

將公式（15）代入 公式（16），得：

λ=Rv?2-μBgω-vμBτb+vτiueq-vτm。 （20）

把公式（20）代入公式（19）得：

S=-λ

=Rv?2μBgω+vμBτb-vτiueq+vτm=0。（21）

整理公式（21）可得到等效控制量：

u∧eq=μ∧Bgωvτi+μ∧Bτbτi+τmτi。（22）

其中，μ∧B為μB最大時的控制量。

若切換控制量選取為：

us=β?sgn?S。（23）

其中，β>0，則系統狀態總能在有限時間內到達滑動模態St=0。

在公式（23）中：

sgn?S=1S>0?-1S>0。（24）

因此，最終滑模控制器設計為：

u=u∧eq+us。（25）

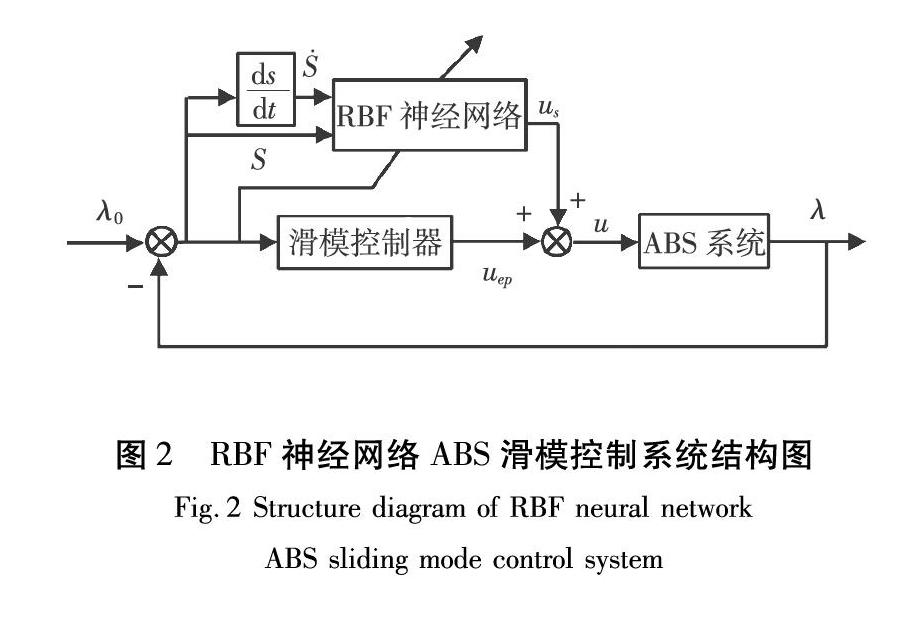
當出現諸如模型不匹配和未建模動態等問題，使系統軌跡偏離滑模面時，系統通過us=β?sgn?S切換控制使系統軌跡趨向滑模面。通過RBF神經網絡，對切換控制中β值進行在線實時調整，使β值盡量減小，從而削弱系統的抖振。其控制系統方框圖如圖2所示。

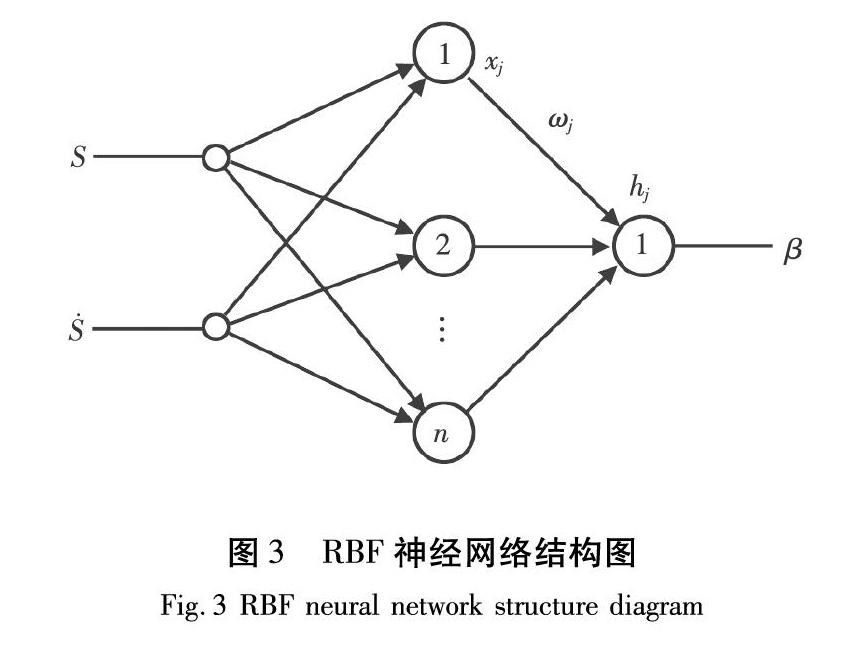
圖2中，滑模控制器用來產生等效控制ueq，RBF神經網絡用來調整切換控制中的參數β值。RBF神經網絡結構如圖3所示。

在圖3中，輸出結點hj由中間節點xj經過權值ωj得到。則結點hj的輸出為：

β=?Σ?jxjωj。（26）

根據滑模控制原理 ，控制目標選為St·St→0，則RBF神經網絡的權值調整指標為：

E=St*St。（27）

由公式（27）得：

d?ωj=-α?E?ωj=-α?StStωj

=-α?StSt?βt?βt?ωj。（28）

式中：α為神經網絡調整步長。

StSt?βt=St?St?βt=-bSt。（29）

βt?ωjt=?exp?-‖S-cj‖?2/bj。（30）

由公式（26）～公式（30）可得，RBF網絡權值增量值為：

dωj=γSt?expexp?-‖S-cj‖?2/bj

=γSthjS。 （31）

進而可給出權值調整算法為：

ωjt=ωjt-1+?d?ωjt+

αωjt-1-ωjt-2?。 （32）

3仿真及結果分析

仿真模型參數見表1～表3。

神經網絡采用2個輸入節點分別為滑移率誤差S及其變化率S;采用最大矩陣元法確定40個隱層節點;1個輸出節點為系統切換控制量us。隱層采用高斯函數，輸出層采用線性函數。

汽車ABS系統總體仿真模型如圖4所示，仿真結果如圖5～圖8所示。

圖5～圖8中，紅線為基于RBF神經網絡的滑模控制器控制效果，綠線為普通滑模控制器的控制效果。從圖5速度曲線中可以看出：車速從初始制動速度20 m/s（66.7 rad/s）降到0m/s過程中，采用常規滑模控制器的ABS系統制動時間約為2.598 s，采用基于RBF滑模控制器的ABS系統制動時間約為2.413 s，制動時間減少了約0.185 s;圖6的滑移率曲線可以看出：采用基于RBF滑模控制器的系統比采用常規滑模控制器的系統到達最優滑移率的時間減少了約0.087 s;圖7的制動力矩曲線可以看出：采用基于RBF滑模控制器的系統比采用常規滑模控制器的系統穩定于最大制動力矩的時間減少了0.175 s;圖8的制動距離曲線可以看出：采用常規滑模控制器的ABS系統的制動距離約為25.75 m，采用基于RBF滑模控制器的ABS系統的制動距離約為23.87 m，制動距離減少了約1.88 m。仿真結果表明：采用基于RBF的滑模控制器的系統的響應速度更快，系統更穩定，控制效果更優。

4結束語

滑模控制具有算法簡單、對模型要求低、響應速度快以及魯棒性強等優點，非常適合林區作業貨車的控制要求。但由于其非線性的特性使得控制信號會產生高頻抖振。本文從削弱抖振的角度出發，利用神經網絡算法的自學習能力，設計了新的林區貨車ABS滑模變結構控制器，通過仿真實驗結果分析，驗證了本文所設計的控制算法在林區貨車ABS控制中的有效性。

【參考文獻】

[1]黃銳，王森，喬華.淺析汽車制動防抱制動系統（ABS）[J].時代汽車，2018（7）：133-134.

HUANG R， WANG S， QIAO H， et al. Analysis of car brake anti-lock braking system（ABS）[J]. Times Car， 2018（7）： 133-134.

[2]凌濱，宋夢實，邢鍵，等.基于模糊PID的汽車防抱死制動系統[J].計算機仿真，2018，35（10）：166-170.

LIN B， SONG M S， XIN J， et al. Automobile anti-lock braking system based on fuzzy PID[J]. Computer Simulation， 2018， 35（10）：166-170.

[3]CHUN K， SUN W M. Wheel slip control with moving sliding surface[J]. IEEE Transaction on Automotive Technology， 2004， 5（2）：23-133.

[4]GLAVIC M. Design of a resistive brake controller for power system stability enhancement using reinforcement learning[J]. IEEE Transaction on Control System Technology， 2005， 13（5）：743-751.

[5]張策.基于MATLAB仿真的數字PID控制器設計方法[J].森林工程，2015，31（6）：85-88.

ZHANG C. Design method of digital PID controller based on MATLAB simulation[J]. Forest Engineering， 2015， 31（6）：85-88.

[6]尹鳳杰，井元偉，楊暉.基于模糊滑模控制的主動隊列管理算法[J].東北大學學報：自然科學版，2006，27（5）：473-476.

YIN F J， JIN Y W， YANG H. Active queue management algorithm based on fuzzy sliding mode control[J]. Journal of Northeast University， Natural Science Edition， 2006， 27（5）：473-476.

[7]宋文龍，楊鑫，賈鶴鳴.采摘機械臂的滑模PID控制[J].森林工程，2013，29（2）：74-76.

SONG W L， YANG X， JIA H M. Sliding mode PID control of picking manipulator[J]. Forest Engineering， 2013， 29（2）：74-76.

[8]張強.基于線控技術的防抱死制動系統研究[D].長沙：湖南大學，2013.

ZHANG Q. Research on anti-lock braking system based on wire control technology[D]. Changsha： Hunan University， 2013.

[9]付長勝.汽車ABS系統優化及關鍵技術研究[D].贛州：江西理工大學，2016.

FU C S. Research on optimization and key technology of automobile ABS system[D]. Ganzhou： Jiangxi University of Science and Technology， 2016.

[10]丁凡一，孫振偉，李智鑫，等.基于51單片機的輪胎自動加氣裝置[J].林業機械與木工設備，2017，45（2）：46-48.

DING F Y，SUN Z W，LI Z X， et al. 51SCM-based Automatic Tire Inflating Devices[J].Forestry Machinery & Woodworking Equipment，2017，45（2）：46-48.

[11]邊明遠.用于縱向道路附著系數評估的簡化輪胎模型[J].重慶理工大學學報，2012，26（1）：1-5.

BIAN M Y. Simplified tire model for evaluation of longitudinal road adhesion coefficient[J]. Journal of Chongqing University of Technology， 2012， 26（1）：1-5.

[12]邊明遠，李克強.基于雙指數模型的縱向附著系數計算模型[J].農業機械學報，2005，36（5）：5-8.

BIAN M Y， LI K Q. Calculation model of longitudinal attachment coefficient based on double exponential model[J]. Journal of Agricultural Machinery， 2005， 36（5）：5-8.

[13]彭曉燕.汽車線控制動系統安全控制技術研究[D].長沙：湖南大學，2013.

PENG X Y. Research on safety control technology of automobile wire brake system[D]. Changsha： Hunan University， 2013.

[14]陳思成，陳劭，楊越.森林消防車制動安全性評價與試驗研究[J].林業機械與木工設備，2015，43（11）：10-13.

CHEN S C，CHEN Z，YANG Y. Forest fire engine braking safety evaluation and experimental research [J].Forestry Science & Technology，2015，43（11）：10-13.

[15]徐雯靜，宋蟄存.永磁同步電機一種新型滑模觀測器的設計[J].森林工程，2014，30（6）：75-79.

XU W J， SONG Z C. Design of a new sliding mode observer for permanent magnet synchronous motor[J]. Forest Engineering， 2014， 30（6）：75-79.

[16]陳昌榮.基于滑移率的車輛線控制動系統ABS控制研究[D].長沙：湖南大學，2010.

CHEN C R. Study on ABS control of vehicle brake system by wire control based on slip ratio[D]. Changsha： Hunan University， 2010.

[17]沈沉，王軍，林逸.電子機械制動系統制動執行器建模與試驗[J].農業機械學報，2007，38（8）：30-33.

SHEN C， WANG J， LIN Y. Modeling and test of brake actuator in electro-mechanical braking system[J]. Journal of Agricultural Machinery， 2007， 38（8）：30-33.

[18]張文海.用反電勢系數計算直流力矩電機堵轉轉矩的公式[J].微特電機，2004（4）：45-46.

ZHANG W H. A formula for calculating the torque of DC torque motor by using the back EMF coefficient[J]. Micro Special Motor， 2004（4）：45-46.

[19]張靜，裴雪紅.基于RBF在線辨識的PID整定[J].電機與控制學報，2009，13（1）157-160.

ZHANG J， PEI X H. PID tuning based on RBF online identification[J]. Journal of Motor and Control， 2009， 13（1）：157-160.

[20]裴雪紅.基于改進RBF神經網絡的PID控制[D].哈爾濱：哈爾濱理工大學，2010.

PEI X H. PID control based on improved RBF neural network[D]. Harbin： Harbin University of Technology， 2010.

[21]李巖，蘇學軍.基于模糊徑向基函數神經網絡的PID控制算法仿真研究[J].自動化與儀器儀表，2014（9）：1-2.

LI Y， SHU X J. Simulation of PID control algorithm based on fuzzy radial basis function neural network[J]. Automation and Instrumentation， 2014（9）：1-2.