基于改進鯨魚優化算法的物流配送中心選址策略
尚 猛 康建英 曹峻瑋 萬志鵬
1(安陽工學院飛行學院 河南 安陽 455000)2(河北經貿大學經濟與管理學院 河北 石家莊 050091)3(嶺南大學經營學院 韓國 慶山 385141)
0 引 言
隨著電子商務的迅速發展,人們對于物流配送效率的要求也越來越高。物流配送中心選址作為物流調度配送問題中的核心問題,起到了中心樞紐的作用,很大程度上決定了物流配送系統的配送模式和配送體系。如何在多個配送地址中合理有效地選取配送中心地址是提高物流配送效率的有效途徑,具有重要的現實意義。物流配送中心選址模式屬于非線性模型,具有較多復雜的約束條件以及不光滑特性[1],可歸于NP-hard問題。近年來,國內外的研究學者對于物流配送選址問題進行了深入的研究,提出了層次分析法、智能優化算法、重心法和動態規劃法等,在解決物流配送中心選址的問題上取得了突破性的進展[2]。
袁群等[3]提出了一種基于改進混合遺傳算法的物流配送中心選址方法。胡琳等[4]提出了一種基于改進粒子群優化算法的物流配送中心選址策略。馬毓嚀等[5]提出了一種免疫粒子群算法的物流配送中心選址策略。王坤等[6]提出了一種基于蟻群算法的物流配送中心選址策略。周歡等[7]提出了一種基于布谷鳥算法的電子商務物流配送中心選址策略。卓婧婧等[8]提出了一種基于樹型動態規劃的物流配送中心選址算法。王朋等[9]提出一種基于重心法的物流配送中心選址。但當物流配送點較多時,單一機制的優化算法在尋優過程中很容易陷入局部最優,降低算法的搜索能力,最后的尋優結果較實際情況易出現較大偏差。
針對上述問題,本文提出一種改進的鯨魚優化算法物流配送中心選址策略。針對傳統的鯨魚優化算法[10]易陷入局部最優和收斂精度低的問題,本文首先通過引入綜合變異算子加強了算法的全局搜索能力,提高了算法的收斂精度。其次加入了隨機正弦慣性權重,提高了算法的局部搜索能力和種群多樣性,防止算法因喪失種群多樣性陷入局部最優。最后將改進的鯨魚優化算法用于物流配送中心選址問題上,解決了因物流配送點過多引起的選取偏差過大的問題。
1 物流配送中心選址數學模型
物流配送中心選址問題可理解為從N個物流中心備選點中選取M個需求點作為配送中心。由于各配送中心所處地理位置和建設成本的不同,因此,建立帶多種約束條件的物流配送中心選址數學模型的目標函數為:
(1)
式中:N為物流配送的全部地址;M為所選出的全部配送中心地址;Fj為每個配送中心的建設費用;hj為0或1,當hj=1時,Fj為配送中心;ψi,j為第i個配送點的需求量;di,j為第i個配送點和與其距離最短的第j個配送中心之間的距離;Zi,j為0或1,當Zi,j=1時,表示配送點i的需求貨物由配送中心供應。
物流配送中心選址問題的約束條件為:
(2)
式(2)表示每個配送點的所需量(所需貨物總量)皆應小于等于與其對應配送中心的貨物總量。
(3)
式(3)表示每個配送點的所需貨物只可從距配送點最近的配送中心發貨。
Zi,j≤hjj=1,2,…,N
(4)
式(4)表示無配送中心的點沒有客戶。
(5)
式(5)表示產生P個物流配送中心。
di,j≤t
(6)
式6表示每個配送點都應在與其對應的配送中心可配送范圍之內。
2 鯨魚優化算法
2.1 標準鯨魚優化算法
鯨魚優化算法是澳大利亞學者Mirjalili根據鯨魚獵食方式所提出的一種新啟發式優化算法。WOA由三個搜索階段構成:包圍獵物、螺旋捕獵、隨機搜索。在WOA中,可將每個鯨魚都看做一個粒子,每個粒子的位置均代表一個決策變量。鯨魚在捕獵過程中,并非按直線進行捕食,而是以一種螺旋方式靠近并捕食獵物,其算法流程如下所示:
(1) 包圍獵物:
鯨魚在狩獵時通常會先包圍獵物,其數學模型如下所示:
D=|CX*(t)-X(t)|
(7)
X(t+1)=X*(t)-A·D
(8)
式中:t為當前迭代次數,A和C為學習因子,X*(t)表示目前為止最優的鯨魚位置向量,X(t)表示當前鯨魚所在位置向量。A和C由如下公式得出:
A=2a×r1-a
(9)
C=2×r2
(10)
a=2-2×t/Tmax
(11)
式中:r1和r2為(0,1)之間的隨機數,a的值在(0,2)之間并線性遞減,t為當前的迭代次數,Tmax為最大迭代次數。
(2) 螺旋狩獵:
鯨魚在狩獵過程中,通常會以螺旋運動的方式包圍獵物并進行狩獵,其數學模型如下所示:
X(t+1)=X*(t)+Dp·ebl·cos(2πl)
(12)
Dp=|X*(t)-X(t)|
(13)
式中:Dp為鯨魚和獵物之間的距離,X*(t)為所有迭代至今為止最好的位置向量,b是一個常數,用來定義螺線的形狀,l是(-1,1)中的隨機數。值得注意的是,鯨魚以螺旋狀游向獵物,但同時還要收縮包圍圈。因此,在這種同步行為模型中,假設有Pi的概率選擇收縮包圍機制和(1-Pi)的概率選擇螺旋模型來更新鯨魚的位置,其數學模型如下:
(14)
在鯨魚對獵物進行攻擊時,越接近獵物,a的值就會越小,A的值也就會越小。在算法迭代過程中,由于a的值是從2到0線性遞減的,因此A就成為[-a,a]內的隨機數。當A的值在[-1,1]內時,鯨魚的下一個位置可以是它現在的位置和獵物的位置之間的任意位置。
(3) 搜索獵物:
搜索獵物采用隨機個體位置尋找獵物,其數學模型如下:
D=|CXrand-X(t)|
(15)
X(t+1)=Xrand-A·D
(16)
式中:Xrand是隨機所得的位置向量,算法設定當A≥1時,隨機選擇一個搜索領導個體,并通過領導個體的位置來更新其他鯨魚的位置,以此引導鯨魚離開當前獵物,借此找到更合適的獵物,目的是加強算法的全局搜索能力。
2.2 改進的鯨魚優化算法
鯨魚優化算法作為一種新的啟發式優化算法,更新機制簡單,調整參數少并具有一定的隨機性,相較其他啟發式優化算法具有更高的搜索能力和搜索速度。但由于算法螺旋尋優的更新機制,使得算法很容易陷入局部最優,降低算法的收斂精度。因此本文針對上述問題,在算法尋優過程中引入綜合變異算子和隨機正弦慣性權重,目的是加強算法的全局搜索能力,防止算法陷入局部最優。
首先,從式(7)至式(16)中可知,傳統的WOA優化算法的收斂速度回隨著迭代次數的增加而減慢,在算法迭代后期,越來越多的鯨魚個體逐漸向全局最優解靠近,使得算法的收斂速度快速降低,最終導致算法陷入局部最優,影響WOA算法的收斂精度。針對上述問題,本文提出一種基于非均勻變異和柯西變異相融合的綜合變異策略,其步驟如下所示:
1) 通過設置變異開關函數,通過對開關條件的判斷,對當前鯨魚的位置進行變異操作,其中變異開關的數學表達式如下所示:
(17)
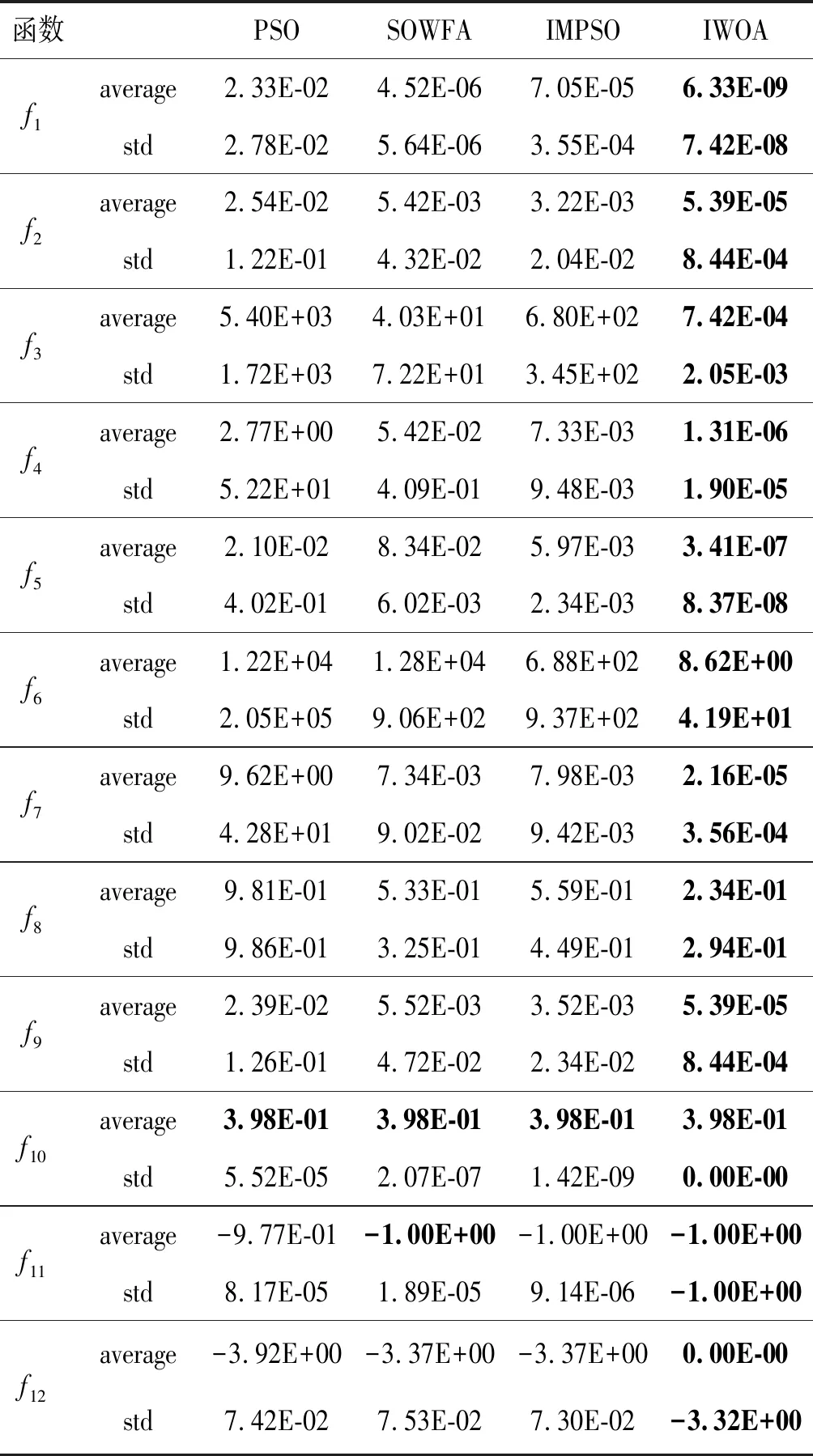
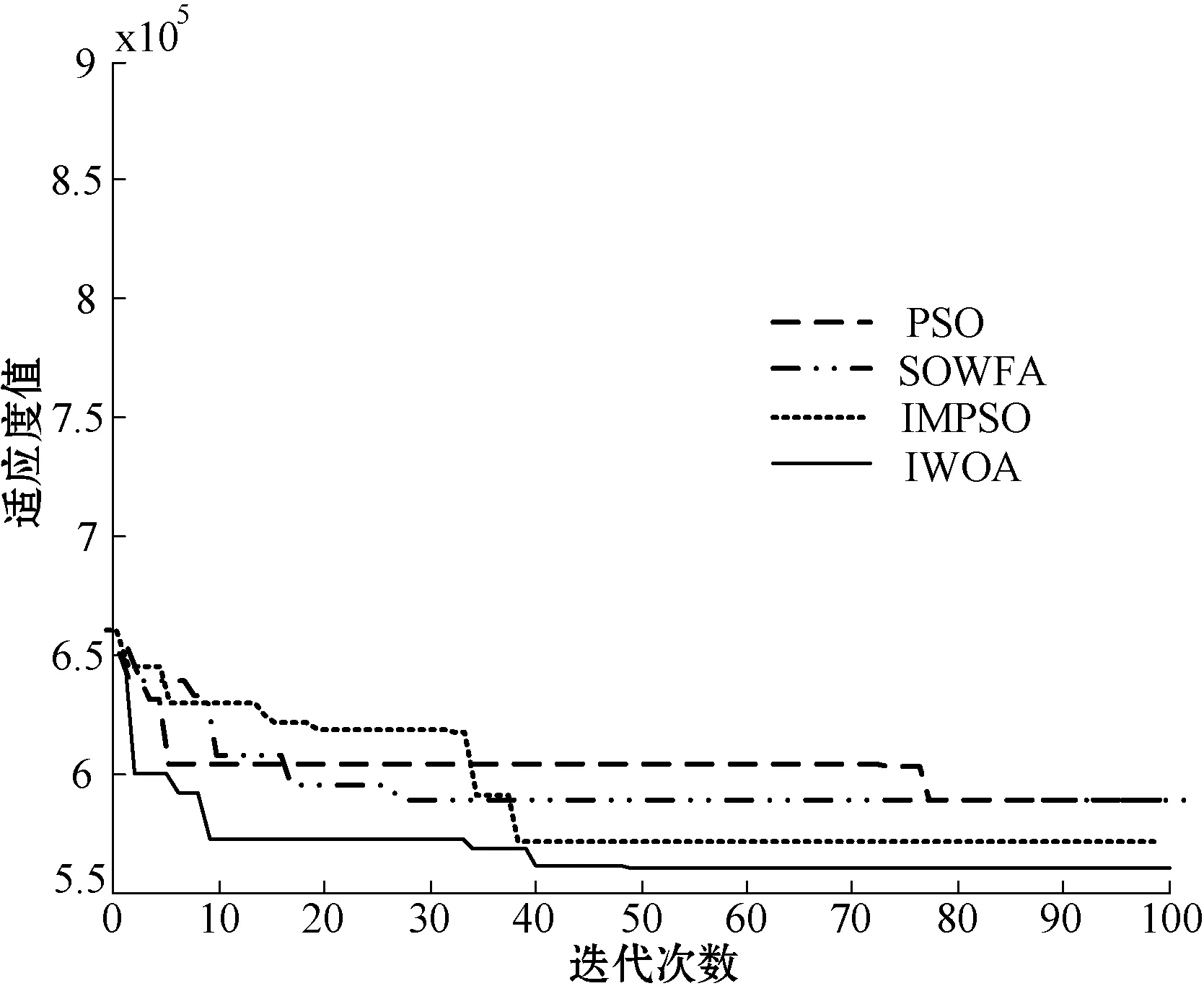
式中:n為維度,SN為鯨魚種群規模。定義當0 2) WOA算法的步長由|A|的值決定,當|A|>1時,此時算法處于迭代前期,算法搜索速度較快,范圍較廣。柯西變異的變異范圍較傳統的二項式變異,多項式變異和非均勻變異等具有更廣,因此在算法處于迭代前期,當粒子選入局部最優時,加入了柯西逆累積分布函數[11],通過柯西變異對粒子施加一個較大的擾動,幫助粒子跳出局部最優。由于WOA算法進行全局搜索時,會通過螺旋運動的方式更新粒子的位置,因此避免了經過柯西變異的粒子會出現盲目變異的情況。其中柯西逆累積分布函數的數學表達式如下所示: F-1(p;x0,γ)=x0+γ×tan(π×(p-0.5)) (18) 因此可將式(16)改進為: X(t+1)=xi,j(t)+A·tan(π×(p-0.5)) (19) 式中:xi,j(t)為第i頭鯨魚的第j個位置,γ=A,0≤p≤1。 3) 當|A|<1時,算法處于迭代后期,應對switch(k)進行判斷,如有小部分鯨魚粒子滿足變異條件,滿足變異條件的粒子會通過非均勻變異移向全局最優解,而不滿足變異條件的粒子則通過原來的位置更新公式向全局最優解靠近,加快了算法的搜索速度,減小了算法在迭代前期陷入局部最優的可能。非均勻變異來源于非均勻變異演化算法[12],與傳統遺傳算法中變異策略有所不同。非均勻變異演化算法在迭代過程中可自適應調整搜索步長,因此當算法處于迭代后期,收斂速度較慢時,將非均勻變異策略與WOA算法相結合,目的是使算法在迭代后期始終都有跳出局部最優的可能,有效克服了算法因早熟易陷入局部最優的問題,提高了算法的全局搜索能力。設鯨魚種群規模為SN,xi={xi1,xi2,…,xin,…,xiSN}T。假設對第n個分量執行變異操作,則其非均勻變異公式為: (20) 其次,通過式(9)至式(11)可知,鯨魚優化算法的全局尋優能力和局部尋優能力完全由參數a的值決定,在迭代后期,a的值線性減小,嚴重影響算法的收斂精度,使粒子極易陷入局部最優,因此本文通過綜合變異策略幫助算法跳出局部最優。本文根據正弦曲線的特性,提出一種隨機正弦慣性權重,目的是為了提高算法的種群多樣性和全局搜索能力。隨機正弦慣性權重的數學表達式如下所示: w=2×(1-sin(0.5×π×(t/tmax)))×rand() (21) 由式(21)可得,算法迭代初期,t/tmax的值趨于0,w較大,算法具有較好的全局尋優能力。算法迭代后期,當t趨近于tmax時,w趨近于0,具有較高的局部搜索能力。rand()為[0,1]之間的隨機數,目的是為了提高算法的種群多樣性,因此式(14)和式(19)可修改為如下形式: (22) X(t+1)=wxi,j(t)+A·tan(π×(p-0.5)) (23) IWOA算法流程如圖1所示。 圖1 IWOA算法流程圖 為了驗證本文所提算法的有效性,本文選取12個基準測試函數對試驗進行測試,其中f1至f4為單峰測試函數,f5至f8為多峰測試函數,f9至f12為固定維測試函數,具體測試函數如表1所示。并與改進粒子群算法PSO[13]、改進煙花算法SOWFA[12]和免疫粒子群算法IMPSO[5]進行對比試驗,迭代次數為100,并將100次的試驗結果求得平均值和最小值,最優解用加粗字體表示,試驗結果如表2所示。 表1 12個測試函數 表2 12個測試函數測試結果 由表2可得,對于單峰函數f1和f2而言,本文所提IWAO相較其他三種算法可以求得更小的平均值和標準差,證明IWAO具有更高的求解精度和穩定性。對于測試函數而言,PSO、SOWFA和IMPSO算法均由于陷入局部最優而過早收斂,但IWAO仍具有較高的求解精度和穩定性,這是由于混合變異的引用使得算法從迭代前期到迭代完成期間,始終具有發生變異的可能,因此,在算法尋優期間,當算法陷入局部最優均可能獲得一個較大的擾動,幫助粒子跳出局部最優。 對于多峰函數f8而言,雖然四種算法的尋優精度均不理想,但IWOA仍優于其他三種算法。這是由于在IWOA中,隨機正弦慣性權重使得算法在迭代過程中始終保持較快的收斂速度并持續向目標解靠近,這一特性是由正弦曲線非線性特性變化所決定,幫助算法在迭代后期也可以充分地進行全局尋優。 對于固定維函數而言,四種算法的收斂精度和穩定性均有提高,這是由于所求目標函數維數較低所致。但對于測試函數f11而言,IWOA算法的標準差更低,說明IWOA相較其他三種算法的穩定性更高,魯棒性更強。整體而言,IWOA算法具有更高的收斂精度和穩定性,算法的整體性能相較基本WOA有較大提高。 通過IWOA算法對物流配送中心選址模型優化時,可將粒子表示為X=[x1,x2,…,xN],N表示物流配送點總數,IWOA算法將在N個配送點中,選取M個配送點作為配送中心。若最終選取的最優粒子X=[1,0,1,1,0,0],表示自在6個配送點中,選取第1、3和4個配送點作為配送中心地址。 為了驗證本文所提基于改進鯨魚優化算法求解物流配送中心選址的高效性,以文獻[5]中的全國31個城市的地理位置和供需量為例進行試驗仿真,通過對比基于改進煙花算法的選址策略SOFWA[12]、免疫粒子群算法的選址策略IMPSO[5]以及改進粒子群算法的選址策略PSO[13]的試驗結果,驗證了本文所提方法的有效性。其中四種算法的迭代次數均為100,每種算法獨立運行50次。城市坐標以及貨物供需量如表3所示,試驗結果如表4和圖2-圖6所示,本文實驗均在Win7 64位操作系統,MATLAB 2014a中進行實驗仿真。 表3 城市地理位置及貨物供需量 表4 四種算法的選址性能比較 圖2 基于IWOA算法的物流配送中心選址 圖3 基于SOFWA算法的物流配送中心選址 圖4 基于IMPSO算法的物流配送中心選址 圖5 基于PSO算法的物流配送中心選址 圖6 基于4種算法的適應度值對比圖 圖2-圖5分別為基于IWOA的選址策略、基于SOWFA的選址策略、基于IMPSO的選址策略和基于改進PSO的選址策略所求解的平均適應度值和最小適應度值。從圖中可以看出,較其他三種算法而言,基于IWOA算法的物流配送中心選址方式在算法初期,所求解的適應度值下降速度更快,說明IWOA算法擁有更好的初值尋優,尋優范圍更廣。并且基于IWOA的選址策略可以求解答到更小的適應度值,說明基于IWOA的選址策略具有更高的求解精度。從表4中可以看出,IWOA所求解的平均配送費用較其他三種算法有較為明顯的降低,很大程度上降低了物流配送的成本,且相較其他三種算法而言,迭代次數明顯減小,算法運行時間也明顯降低,說明IWOA算法收斂速度更快,求解速度更快。總體而言,IWOA算法較其他三種算法,可以更加快速、精確地選取物流配送中心地址。 本文針對物流配送中心選址問題,提出一種改進的鯨魚優化選址策略。針對選址過程中算法出現的陷入局部最優和收斂精度低的問題,提出一種綜合變異策略和隨機正弦慣性權重,加強了算法的全局搜索能力,提高了算法的收斂速度和收斂精度,通過測試函數的對比試驗,驗證了算法的有效性。最后將改進的鯨魚優化算法對物流配送中心選址模型進行優化。試驗結果證明,本文所提方法,很大程度上減小了配送成本,可以快速選擇出合理的配送中心地址。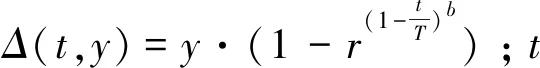

2.3 基于測試函數的性能測試

3 改進的鯨魚優化算法在物流配送中心選址中的應用






4 結 語

