基于波列邊帶不穩定性和阻尼影響的畸形波生成數值研究

張運秋

摘? ? 要：邊帶不穩定性是畸形波生成的一種可能的非線性機理，其數值模擬的實現對于實驗室基于非線性角度生成畸形波及開展畸形波對船舶等海工程結構物的波浪力研究都具有重要的指導作用。本文考慮到實驗室水槽試驗中影響畸形波生成的真實的阻尼作用，以包含阻尼影響的四階修正型深水非線性薛定諤方程和偽譜方法為基礎建立了波浪演化數值模型，通過載波加邊帶擾動的波列的非線性演化來模擬畸形波的生成，并在此基礎上進一步分析阻尼及水槽寬度和擾動頻帶寬度等參數對畸形波生成的影響作用，其結果對于探索畸形波的非線性實驗生成方法將提供有益的幫助。

關鍵詞：邊帶不穩定性;阻尼影響;畸形波;偽譜方法;數值研究

中圖分類號：U661.1? ? ? ??? ? ? ? ? ? ? ? ? ? ? ? 文獻標識碼：A

Abstract： Sideband instability may be a possible nonlinear mechanism of freak wave generation. The realization of its numerical simulation plays an important role in guiding the laboratory to generate deformed waves based on nonlinear angle and to carry out wave force research of freak wave on marine engineering structures such as ships. Considering the real damping effect on freak wave generation in laboratory flume tests， a numerical model of wave evolution is established based on the fourth-order modified deep-water nonlinear Schrodinger equation and pseudo-spectral method including damping effect. The generation of freak wave is simulated by the nonlinear wave train evolution of carrier wave plus sideband disturbance. On this basis， the effects of damping， flume width and disturbance band width on freak wave generation are further analyzed. The results will be helpful for exploring freak wave's nonlinear experimental generation method.

Key words： sideband instability; damping effect; freak wave; pseudo-spectral method; numerical research.

1? ? 前言

畸形波是波高大于兩倍的有效波高和相鄰波高以及波峰大于0.65倍波高的大波[1]。它是海洋工程和學術研究中比較關注的一種災害性波浪。由于其發生地點的不確定性和持續時間的暫時性，在天然狀態下很難捕捉到符合定義[1]的、完整的畸形波記錄。已有的一些偶然得到的或者是長期現場觀測到的少量畸形波數據，使人們對畸形波的基本特點、發生區域及發生條件的多樣性有了初步的認識，但還不足以從本質上了解畸形波的成因及特性。因此，有必要在試驗室中模擬畸形波的生成，獲得更多的實測數據來研究其發生機理及特性，并將其作為極限荷載來研究波浪與結構物作用的規律。

目前，物理模擬畸形波的研究已經取得了一定的進展。Suchithra and Koola[2]利用深水波浪的色散特性，在某位置處聚焦產生了單個大波，該波的波峰與波高的比為0.54，其波高大于相鄰波高的2.9倍;Kuhnlein基于線性波浪理論開發了一個關于極高波群演化的半經驗程序來產生高且陡的波，Clauss[3]通過其程序優化的改進技術在波浪水槽中生成了最大波高Hmax=2Hs，波峰ηc=0.6Hmax的畸形波;Shemer and Goulitski [4]利用振幅和頻率調制的較寬帶寬初始波列水槽中聚焦生成一個高而且陡的畸形波，波峰高度大于造波機處最大波峰高度的3倍，分析表明二階約束波（2nd bound wave）增加聚焦點處的非線性作用;Kriebel[5]提出在實驗室水槽中采用瞬時波列與隨機波列疊加來生成了波高H=2.24 Hs和波峰ηc=0.527H的畸形波;裴玉國等[6]采用調整隨機初相位、Kriebel[11]提出的雙波列疊加和改進的三波列疊加等方法，在實驗室中生成了符合定義[1]的畸形波;Boomgaard[7]研究了實驗室水槽中的波浪聚焦，指出線性理論不足以產生一個足夠聚焦的波，二階波浪生成理論是用來產生一個波浪聚焦信號的最有效的方法; Sundar et al.[8]由造波機產生的一個非線性瞬時波群在聚焦點處聚焦生成畸形波，波高H=2.125 Hs，波峰ηc=0.685H，其相鄰最大波高約為1.25 Hs。江文山[9]于深水區非線性波列調制研究的T091試驗中統計到了遠大于相鄰波高的大波，認為該結果給出了邊帶不穩定性生成畸形波的一個解釋，該實驗中波高的最大放大因子為2.26，波峰的最大放大因子為2.95，并且在多次實驗中觀測到了類似的瞬時大波。

總的來說，目前畸形波的物理模擬技術還主要是線性理論方面的波浪聚焦，模擬出來的畸形波大多與定義[1]有一定的差別，考慮到畸形波的強非線性特點，需要加強這種極限波浪的非線性生成技術以利于探索畸形波的生成機理及其對結構物作用方面的研究。因此，在實驗室中通過邊帶不穩定性機理，采用深水非線性波列演化方法生成畸形波，是物理模擬畸形波生成可考慮的一個發展方向。而波浪在實驗水槽中的演化或多或少都會受到一些阻尼影響，尤其是較窄的水槽，因此，本文將以考慮阻尼作用的四階修正非線性薛定諤方程[10]和偽譜方法為基礎建立波浪演化數值模型，來探索實驗室中通過深水非線性波列演化生成畸形波的可行性以及有效性。

2? ?數值模型

2.1? 控制方程

影響波浪行進的阻尼主要考慮粘性耗散的作用，假設它是邊界層處耗散的主要因素，由于邊界層區域在各向尺度與一個波長相當的流體體積中僅占極小的比例，則在幾個波長的距離和幾個周期的時間內，對波動的全局影響甚微;然而對遠大于波長的長距離和遠長于周期的長時間來說，粘性有累積效應，是不可低估的。因此，本文采用考慮粘性阻尼作用的四階修正非線性薛定諤方程來研究波浪水槽中波列的演化。群速度移動坐標系統下的無因次方程[10]為：

2.2? 數值方法

方程（1）為高階非線性方程，主要采用偽譜方法（Lo and Mei，1985）[10]來快速求解，偽譜方法以傅立葉變換為基礎，因此方程的求解總是在一個周期為2π域上進行。復波包A在傅立葉空間上的變換及逆變換表示為：

2.3? 邊帶擾動及不穩定性條件

3? ?數值計算結果及討論

邊帶不穩定性是畸形波生成的一個主要可能原因，但其演化受多種相關因素的影響，因此將邊帶不穩定性的演化與畸形波的生成結合起來，來分析各種因素對畸形波生成的影響以及如何在物理試驗中快速獲取畸形波。

3.1? 擾動頻帶寬度的影響

擾動頻帶寬度是載波與邊帶擾動之間的頻率偏差，亦即相鄰邊帶之間的頻率偏差。無因次的擾動頻帶寬度為Δω/ω=γε。對于確定的波陡，尺度因子γ決定著擾動頻帶寬度的大小，也決定著不穩定域內不穩定邊帶的多少。

計算中取邊帶擾動振幅S=0.05，載波的基頻f =2 Hz，波陡ka=0.15，實驗室水槽寬度B=1 m。根據公式（9）可知，當尺度因子0<γ<1.15時，邊帶擾動是不穩定的。在該不穩定域內調整尺度因子的大小，亦即調整擾動頻帶寬度或不穩定邊帶的多少來模擬畸形波的生成。

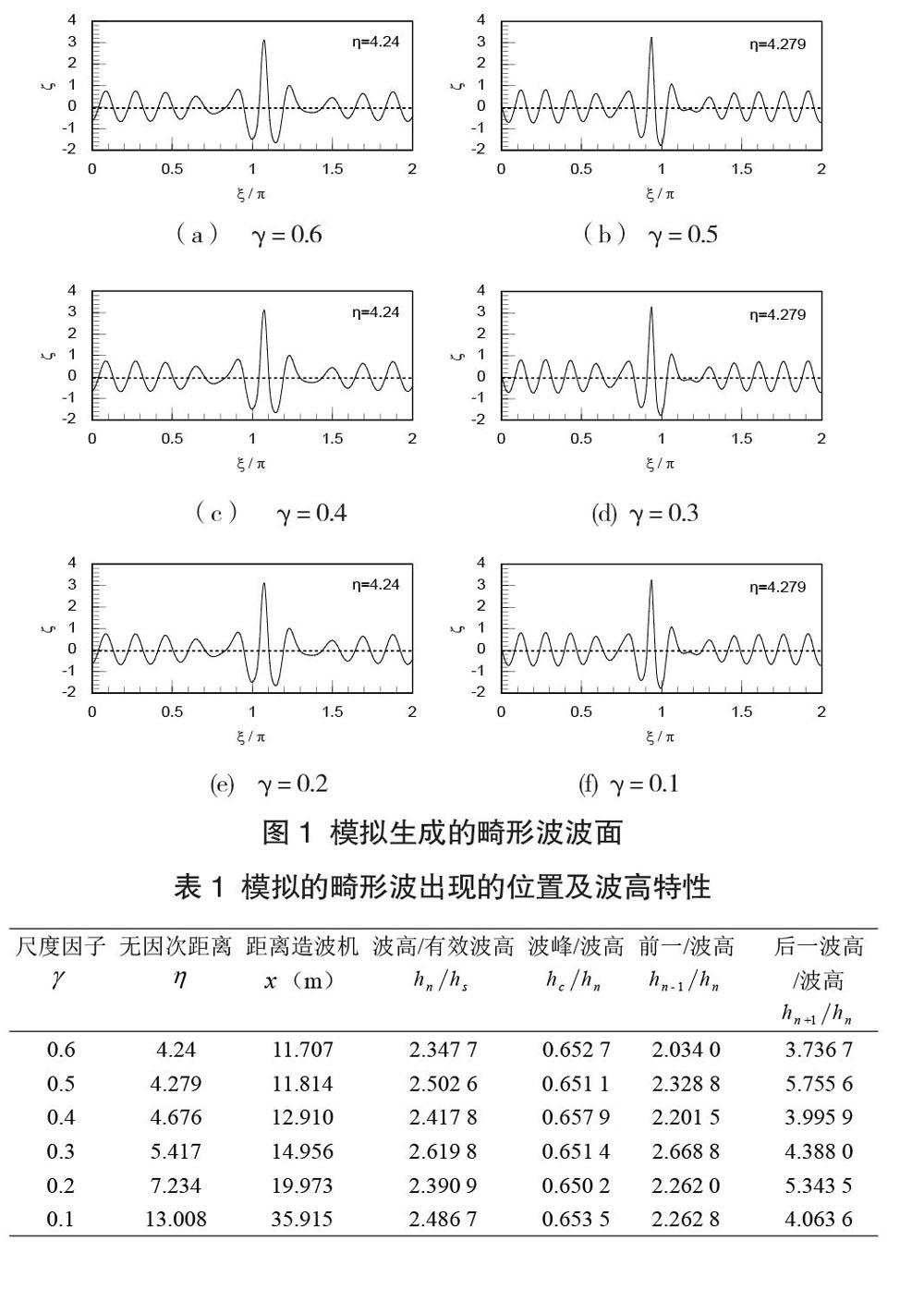
模擬中采用上跨零點法統計波高，取載波波高為有效波高，通過前面給出的定義判斷波列演化過程中畸形波的出現。圖1給出了尺度因子取不同值時畸形波首次出現時的波面，圖中近于正弦波的波面上突然升起了一個高且陡的大波。設該大波為波列中第n個波，波高為hn，波峰高度為hc，該大波前后相鄰波高為hn-1和hn+1。該大波生成的位置及波高特性如表1所示，所生成的大波波高與有效波高的比值均大于2，大于前一波高的2倍，大于后一波高的3～5倍，波峰與波高比大于0.65倍，波面垂直不對稱性明顯，表現出較強的非線性特征，完全符合畸形波的定義;隨著尺度因子的減小，畸形波的生成位置距造波機越來越遠，但與尺度因子并無線性關系，因此物理模擬中以數值結果為輔助更易于捕捉畸形波。

畸形波的生成與波列演化過程中載波與不穩定邊帶間的能量交換相關，為了解波列空間演化過程中畸形波生成的情況，圖2給出了移動坐標系統下無因次的空間上畸形波出現的位置和載波v=0及邊帶v=±1，±2譜振幅的演化。圖中畸形波出現的位置基本對應著載波能量的第一次降低至極值位置附近，這主要是由于粘性阻尼的耗散作用，載波及兩對邊帶的能量隨著演化距離的增加而不斷遞減，使得無阻尼作用下譜演化的類周期性質被改變，因此波列演化過程中多在載波能量第一次下降至極值位置附近易觀測到畸形波的出現。另外，隨著尺度因子的減小，在較近的距離上都可以統計到畸形波，說明生成的畸形波傳播的距離有所增長，有利于物理模擬中捕捉到畸形波。需要特別指出的是，數值模擬中γ=0.2時在某一個位置周期為2π的波面上統計到了2個畸形波，說明較多對不穩定邊帶之間的強非線性相互作用抵消了部分粘性阻尼作用，有利于物理試驗中得到畸形波。

3.2? 初始擾動振幅的影響

初始擾動振幅的大小決定了擾動邊帶初始能量的大小，影響著不穩定邊帶的發展。計算中取邊帶擾動振幅S=0.1，0.05，0.01，載波的基頻f =2Hz，波陡ka=0.15，實驗室水槽寬度B=1 m。圖3給出了上述條件下尺度因子γ=0.7時波列演化過程中畸形波出現的位置統計和載波v=0及邊帶v=±1，±2譜振幅的演化。如圖所示，隨著初始擾動振幅的減小，載波v=0及邊帶v=±1，±2的譜振幅曲線變化至極值的頻率降低，畸形波生成的概率也因此減少。由前面的模擬可知，因阻尼的作用，畸形波的出現大多位于載波能量下降至極值位置附近，而圖中僅有初始擾動振幅S=0.1時的模擬中在該位置附近出現了畸形波，說明較大的初始擾動振幅增加了畸形波生成的可能性，并且也縮小了生成位置的空間距離。顯然初始擾動振幅的增加，增加了不穩定邊帶v=±1的初始能量，加快了調制不穩定性的演化，使得載波v=0譜振幅下降至極值的幅度增加，向不穩定邊帶v=±1轉移的能量也隨之增加，從而利于物理模擬中獲取畸形波。

3.3? 水槽寬度的影響

由公式（3）可知，水槽寬度B的取值影響阻尼的大小，隨著水槽寬度的增加，阻尼減小。計算中取邊帶擾動振幅S=0.05，載波的基頻f = 2 Hz，波陡ka=0.15，水槽寬度B=3.0，2.0，1.5，1.0 m。圖4給出了水槽寬度變化對于畸形波的生成以及相應的譜振幅演化的影響。從圖中可看出，對于γ=0.7只有一對邊帶v =±1不穩定時，隨著水槽寬度的增加，載波v=0及邊帶v =±1，±2的譜振幅變化的幅度增加，即初始波列中被阻尼耗散掉的能量逐漸減少，當水槽寬度B=3 m時，載波v=0及邊帶v=±1，±2的演化已基本接近于無阻尼狀態的演化;而波列演化過程中，畸形波的生成都集中在載波v=0譜振幅第一次下降至最小值位置附近，但畸形波的傳播距離隨之增加，然而因較大的阻尼作用下單位寬度的水槽中并無畸形波出現。因此物理模擬畸形波試驗中，若選較大的尺度因子，亦即較大的無因次頻帶寬度，則需要水槽寬度也相應增加。

3.4? 波陡的影響

波陡ε=ka，由試驗經驗可知，較陡的波列易發生邊帶不穩定性[C.C. Mei，1989]。根據公式（9）可知，給定載波頻率f，波陡的變化不僅影響著邊帶的不穩定域的大小，而且還影響邊帶的帶寬。當ka=0.2，0.15，0.1時，所對應的不穩定域分別為0<γ<1.07、0<γ<1.15、0<γ<1.23。計算中取S=0.05，f =2 Hz，ka=0.15，B=1m，調整不穩定域內的尺度因子大小來模擬畸形波的生成。圖5給出了尺度因子γ=0.9時波陡變化對于載波及邊帶的譜振幅演化及其過程中畸形波的生成影響情況。隨著波陡的增加，載波v=0及邊帶v=±1，±2的譜振幅曲線變化至極值的頻率稍有降低，但由于無因次的空間距離與實際距離之間存在著一個波陡平方的系數關系，并沒有使畸形波可能生成的位置距造波機越來越遠，而是在很大程度上變近了;另外，由于不穩定邊帶v=±1的非對稱增長逐漸加強從而導致了ka=0.2時有畸形波生成，但阻尼的耗散作用使得譜振幅首次極值后再無畸形波出現。因此，物理模擬中適當地增加波陡，不僅有利于畸形波的生成，而且可減少畸形波生成的距離。

4? ? 結語

本文以考慮阻尼作用的四階修正NLS方程為基礎研究了數值試驗水槽中畸形波的生成。通過不穩定邊帶的譜演化分析并結合畸形波的出現位置統計，討論了擾動頻帶寬度、初始擾動振幅、水槽寬度、波陡等因素對實驗室生成畸形波的影響，可以得到如下結論：

（1）由于粘性阻尼的耗散作用，畸形波僅在水槽中不穩定邊帶譜振幅演化的首次極小值位置處出現，因此捕捉畸形波的儀器應設在該處;

（2）畸形波生成的位置與造波機間的距離與擾動頻帶寬度、初始擾動振幅、水槽寬度、波陡等因素并不呈線性關系變化，因此物理試驗中以數值結果為輔助更易于捕捉畸形波;

（3）適當地減小頻帶寬度，或增加初始擾動振幅，或選用較寬的水槽，或增加波陡，有利于物理模擬中生成畸形波，但生成的位置會有所改變。

參考文獻

[1]Klinting， P. and Sand， S.， 1987. Analysis of prototype freak waves， Coastal??Hydrodynamics， ASCE.

[2]Suchithra， N. and Koola， P. M.， 1995. A study of wave impact on horizontal slabs.?Ocean Engineering， 22 （7）.

[3]Clauss， G. F.， 2002. Dramas of the sea： episodic waves and their impact on offshore 、structures. Applied Ocean Research， 24（3）.

[4]Shemer， K.， Goulitski， E K.， 2006. Evolution of wide-spectrum unidirectional wave 、groups in a tank： an experimental and numerical study. European Journal of Mechanics B/Fluids.

[5]Kriebel， D. L.， 2000. Efficient Simulation of Extreme Waves in a Random Sea. In：?Abstract for Rogue waves 2000 workshop， Brest.

[6]裴玉國， 2007. 畸形波的生成及其基本特性分析： （博士學位論文）. 大連理工大學.

[7]Boomgaard， M. V. D.， 2003. Wave focusing in a laboratory flume： （Master's Thesis）.??Holland： Delft University of Technology.

[8]Sundar， V.， Koola， P. M. and Schlenkhoff， A. U.， 1999. Dynamic pressures on inclined?cylinders due to Freak waves. Ocean Engineering， 26（9）.

[9]江文山， 2005. 深水區非線性波列調變之研究： （博士學位論文）. 臺灣： 國立、成功大學.

[10]Lo， E. and Mei， C. C.， 1985. A numerical study of water-wave modulation based on a??higher-order nonlinear Schr?dinger equation. J. Fluid Mech.， 150.

[11]Dysthe， K. B.， 1979. Note on a modification to the nonlinear Schr?dinger equation for?application to deep water waves. Proc.R. Soc. Lond. A， 369.

[12]Mei， C.C.， 1989. The applied dynamics of ocean surface waves. World scientific.