基于OpenSees的鋼筋混凝土平面框架抗連續倒塌能力分析

易偉建 鄧茜

摘? ?要：采用Pushdown方法對移除柱后的鋼筋混凝土平面框架進行抗連續倒塌能力分析. 探究樓層層數對結構抗連續倒塌承載力的影響以及移柱后結構的空腹桁架效應，同時提出一種計算移柱后鋼筋混凝土框架結構體系可靠度的方法. 通過對約束梁、單層平面框架和多層平面框架的擬靜力試驗進行模擬，驗證基于OpenSees建立的有限元模型的正確性. 分別對2層、4層、6層及8層的4跨鋼筋混凝土平面框架進行分析，得到其Pushdown曲線及框架梁軸力曲線，通過Pushdown曲線計算承載力放大系數，利用框架梁鋼筋應變的相對大小設定框架梁層間相關性. 結果表明：隨著樓層的增加，單層平均承載力降低，結構體系連續倒塌概率增大.

關鍵詞：非線性靜力方法（Pushdown）;連續倒塌;平面框架;空腹桁架作用

中圖分類號：TU375.1 ? ? ? ? ? ? ? ? ? ? ? ? ? ?文獻標志碼：A

Abstract： The progressive collapse resistance of reinforced concrete plane frames removed post column was analyzed based on Pushdown method. The effect of the floor layers on the progressive collapse resistance capacity and the vierendeel action of the damage structure was investigated. At the same time，a method for calculating the system reliability of the reinforced concrete frame structure removed post column was proposed. By simulating static test of constrained beam，single-layer plane frame and multi-layer plane frame，the correctness of the finite element model based on OpenSees was verified. The 2，4，6 and 8-layer reinforced concrete frames were analyzed，and the Pushdown curve and the frame beam axis force curve were obtained. The bearing capacity enlargement coefficient was calculated by the Pushdown curve，and the correlation between the frame beams was set by the relative size of the strain of the frame beam. The results show that with the increase of storey，the average bearing capacity of single story decreases，and the probability of progressive collapse of structural system increases.

Key words： Pushdown;progressive collapse;plane frame;vierendeel action

1968 年Ronan Point公寓由于18層發生燃氣爆炸造成結構的一部分整體垮塌，自此結構的抗連續倒塌開始引起工程界的關注. 所謂連續倒塌破壞，是指由于偶然荷載使結構產生局部破壞，并且局部破壞向結構其他部位擴展從而引起結構的大范圍倒塌或整體倒塌[1].50年來，國內外學者對鋼筋混凝土框架結構的抗連續倒塌能力進行了大量試驗與理論研究. 如：Yu[2]以及初明進等[3]通過雙跨梁對子結構的壓拱機制和懸鏈線機制進行研究;易偉建等[4]對縮尺框架結構進行抗連續倒塌試驗研究;Sasani等[5-6]對框架抗連續倒塌空腹桁架作用進行研究;李易等[7-8]通過能量法對結構抗連續倒塌進行抗力需求分析;周育瀧等[9]提出了壓拱機制計算模型等.

Pushdown分析與結構抗震中常采用的Pushover分析相似. Pushover分析主要針對結構側向倒塌，而Pushdown分析主要針對結構豎向倒塌，在結構上逐漸加大豎向荷載，直到結構發生豎向倒塌，通過其荷載-位移曲線研究結構的豎向倒塌機制及豎向極限承載力.

本文采用有限元軟件對鋼筋混凝土（RC）框架結構進行非線性靜力Pushdown分析，研究了RC框架結構的豎向倒塌機制承載力的變化以及損傷結構的空腹桁架效應，同時提出一種新的計算結構體系可靠度的方法.

1? ?OpenSees分析模型

選用OpenSees（OpenSystem for Earthquake Engineering Simulation）開源有限元軟件進行數值分析，其具有強大的非線性模擬功能、豐富的材料庫與單元庫、開放的源代碼以及多種高效的算法. 本文選用Concrete02、Steel02材料，Beam With Hinges單元對框架結構進行模擬.

1.1? ?混凝土本構模型

混凝土選用Concrete02模型（修正的Kent-Park[10] 模型）. 該模型考慮了裂縫間混凝土的受拉強化作用，通過調整混凝土受壓曲線的峰值應力應變和受壓軟化的斜率來考慮箍筋的橫向約束作用. Concrete02本構模型的特點是能夠較好地獲得數值模擬的簡化與精確之間的平衡.

1.2? ?鋼筋本構模型

鋼筋選用Steel02模型. 該模型由Menegotto和Pinto[11]提出，后經Spacone[12]等修正. Steel02模型考慮了鋼筋等向應變硬化，并采用顯函數表達應變，因此Steel02在計算上非常有效率. Steel02本構模型的特點是計算的高效性和準確性.

1.3? ?截面模型

截面模型選用纖維模型（Fiber Model），纖維模型是按一定的尺寸把鋼混凝土梁、柱構件橫截面分割成一定數目的離散纖維，每根纖維的力學特性用混凝土、鋼筋的應力應變曲線分別表示. 纖維模型的使用滿足一定的假定，同時考慮了軸力與彎曲的耦合作用. 纖維模型的特點是物理概念明確，對材料的真實反映，保證分析結構的可靠性.

1.4? ?單元模型

單元模型采用Beam With Hinges單元模型. Beam With Hinges單元的理論基礎是有限單元法柔度理論，此單元模型是一種較為精細的塑性鉸單元模型，構件的兩端設定長度合理的塑性鉸，通過Gauss-Radau積分模擬分析構件的非線性反應，而構件中間區段依然處于彈性階段.

構件進入大撓度階段，OpenSees基于協同轉動方法（Corotational Transformation）[13]進行分析，計算構件的大位移大轉角. 分析過程中設定單元節點達到某一特定位移表示單元失效，單元模型不考慮鋼筋滑移效應.

2? ?試驗驗證

為了驗證OpenSees對鋼筋混凝土連續倒塌機制模擬的準確性，本文分別從梁構件、單層平面框架及多層平面框架層面上對試驗結果進行數值模擬.

2.1? ?梁構件試驗對比

2015年周育瀧等人完成了8 個鋼筋混凝土單向樓板子結構的抗連續倒塌試驗，研究了截面尺寸、配筋率和有無樓板等參數對梁板子結構連續倒塌承載能力的影響[3]. 本文的分析未考慮樓板作用，因此選取文獻[3]中不帶樓板的B2和B3子結構進行數值模擬. 試件幾何尺寸及截面配筋如圖1所示，具體材料性能參數見文獻[3]，數值模擬與試驗的對比如圖2所示.

2.2? ?單層平面框架試驗對比

2015年何慶峰等人完成了兩榀兩跨單層平面框架試驗，研究了局部構件失效后的鋼筋混凝土平面框架結構抗連續倒塌性能[14].本文選取其中靜力試驗的平面框架進行數值模擬. 試驗框架尺寸及截面配筋如圖3所示，具體材料性能參數見文獻[14]，數值模擬與試驗的對比如圖4所示.

2.3? ?多層平面框架試驗對比

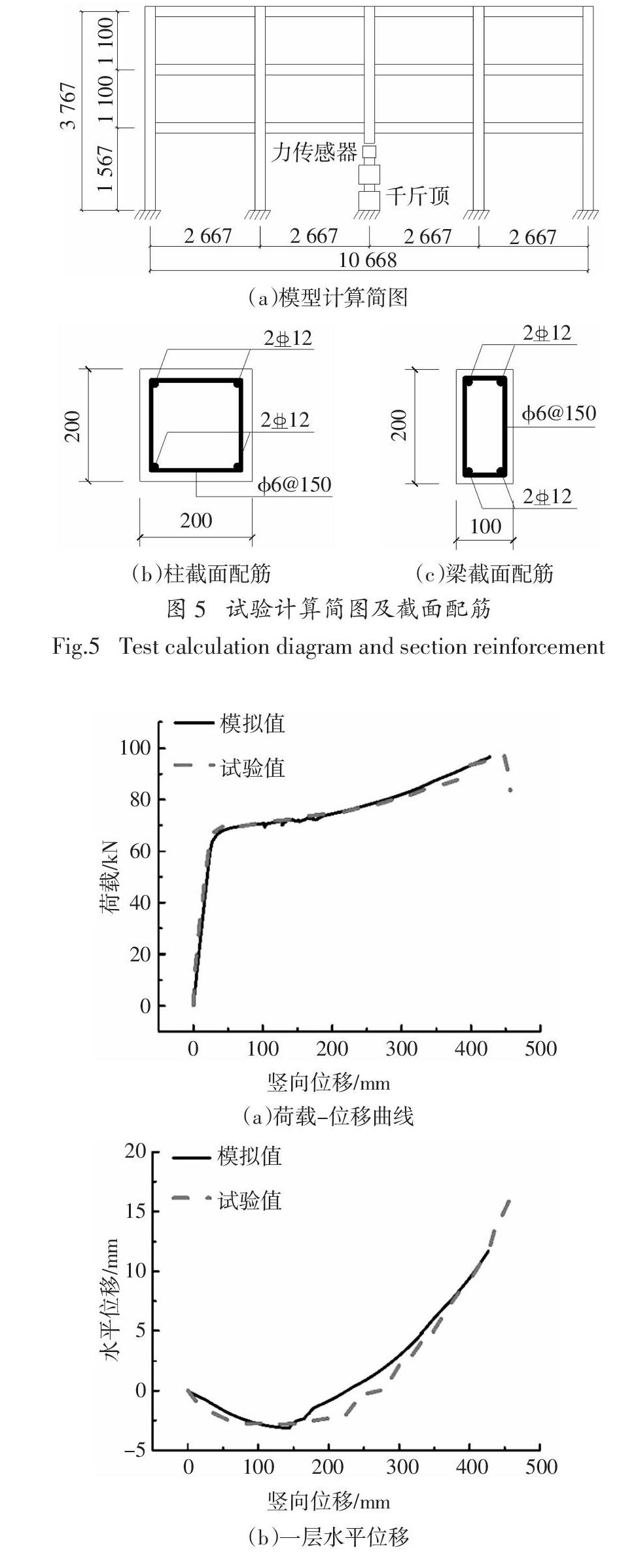
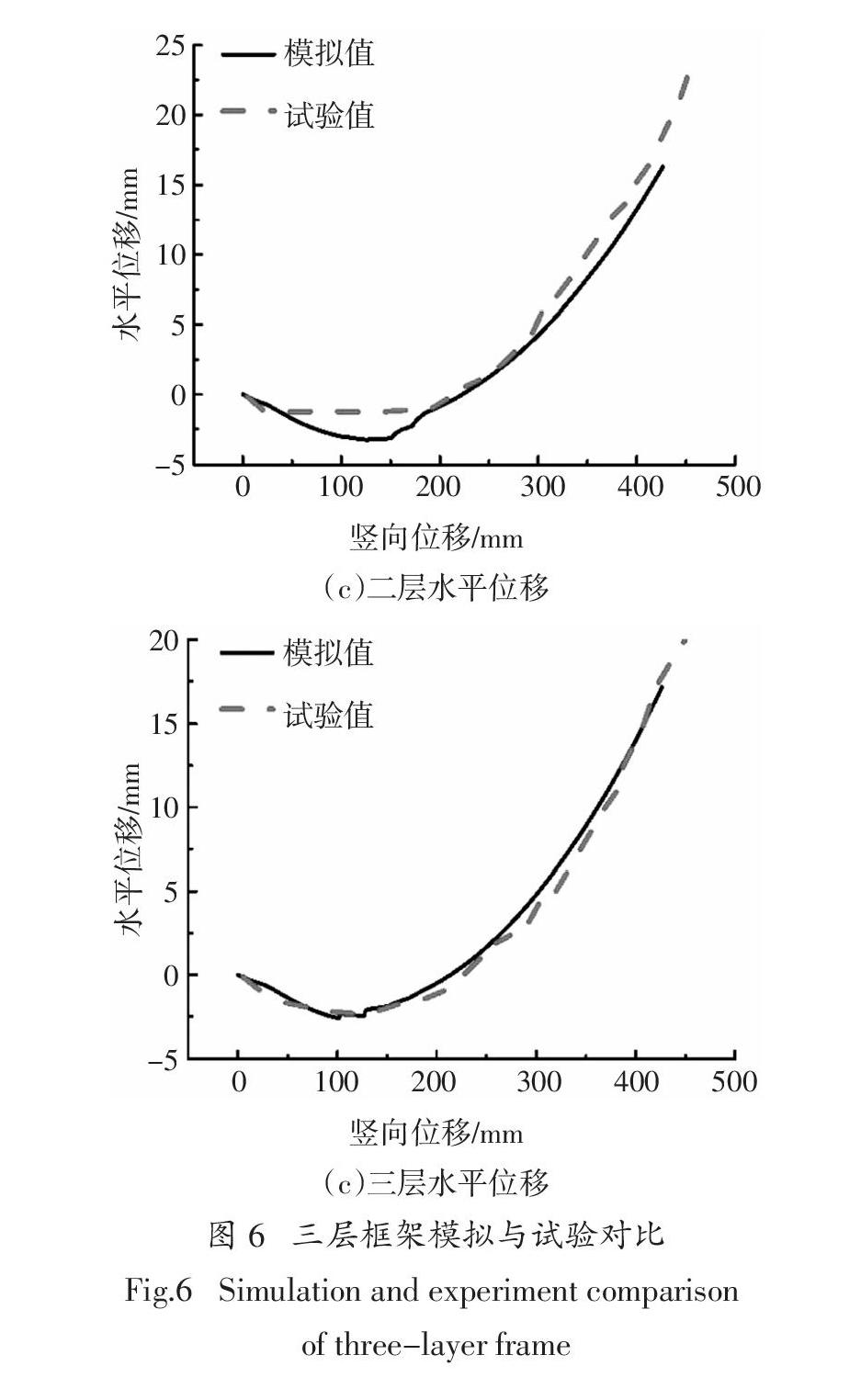
2007年易偉建、何慶峰等人采用擬靜力試驗方法完成了三層四跨平面鋼筋混凝土框架結構的抗倒塌性能試驗，研究了框架結構在倒塌過程中的靜力特性、破壞過程和受力特性[4]. 本文采用前文所述的模型對其進行數值模擬分析. 試件受力簡圖及截面配筋如圖5所示，具體材料性能參數見文獻[4]，數值模擬與試驗的對比如圖6所示.

2.4? ?分析結果的討論

從圖2、圖4、圖6可看出，本文建立的有限元模型能較好地模擬移柱后框架結構連續倒塌的過程. 圖2所示的曲線反映了兩端水平位移受到約束的梁的壓拱機制、轉換機制以及懸鏈線機制;圖4

所示曲線以塑性鉸機制為主. 圖6所示框架結構對移柱后結構可提供一定的約束，豎向位移和水平位移曲線都反映了有限的壓拱機制和懸索機制. 有限元分析結果與試驗曲線良好吻合表明，可以采用本文建立的OpenSees有限元模型對鋼筋混凝土平面框架抗連續倒塌性能進行進一步研究.

3? ?RC框架連續倒塌分析

3.1? ?設計模型

按照現行規范[15]設計一棟多層n榀4跨鋼筋混凝土框架，結構平立面圖如圖7所示. 結構參數如下：結構底層層高為4.7 m，其余層高為3.3 m，橫向跨度各為8 m，縱向跨度各為6 m，柱截面為600 mm×600 mm，梁截面為300 mm×600 mm. 恒荷載標準值取3 kN/m2，活荷載標準值取2 kN/m2，按照雙向板導荷方式計算沿梁長分布的線荷載，即恒荷載為13.88 kN/m，活荷載取9.25 kN/m. 混凝土強度等級為C30，鋼筋等級為HRB400，箍筋等級為HPB300，結構配筋圖如圖8所示. 取其中一榀框架做平面框架分析，為了研究結構樓層變化對連續倒塌承載力的影響，不改變構件尺寸及配筋，分別建立2層、4層、6層、8層框架模型.

3.2? ?非線性靜力Pushdown分析

本文選用Khandelwal[16]等建議的Pushdown分析加載模式進行加載：滿跨加載，即在結構的每一跨包括非損傷跨內均勻地增加豎向荷載. 通過Pushdown方法分析移除中柱后框架結構樓層層數對結構抗連續倒塌承載力的影響以及驗證空腹梁作用的影響.

在Pushdown分析過程中考慮實際構件變形能力的限制，參考DoD 2013[17]的規定，將框架梁失效準則設定為：拆除柱所在支承節點的豎向位移達到與節點連接的最短梁跨度的18%，即0.18l.

3.3? ?不同層數框架結構承載力分析

圖9給出了不同層數框架結構在中柱移除后的Pushdown曲線. 從圖中可看出，不同樓層數的框架移柱后的荷載-撓度曲線相差不大，壓拱機制不十分明顯. 2層框架移柱后的荷載-位移曲線表現出一定的壓拱機制、轉換機制以及懸鏈線機制. 圖10給出了不同樓層框架結構梁軸力的變化情況. 不同樓層框架結構對應的結構壓拱機制承載力和懸鏈線機制承載力計算見表1.

圖9及表1均表明隨著樓層的增加，壓拱機制和懸鏈線機制承載力均有所降低. 在壓拱機制階段，框架梁中軸壓力的存在能顯著提高梁的承載力. 在多層框架結構中，只有軸壓力大的樓層才能獲得更大的壓拱承載力. 如圖10所示，隨著樓層層數的增加，有較大軸壓力的樓層層數并未相應地增加，同時移柱位置上方框架梁中軸壓力值也沒有大幅度增加，因此由于軸壓力產生的壓拱承載力隨著樓層的增加被不斷稀釋，導致這一階段單層平均承載力不斷減小. 在懸鏈線機制階段，移柱后底層梁的軸力由受壓變為受拉. 從圖10也可看出，框架頂層梁始終受壓，懸鏈線機制將導致底層梁產生軸向拉力，移柱上方第二層梁也產生軸拉力，越往上走，內力的轉化越滯后. 因此與壓拱機制階段類似，隨著樓層層數的增加，單層平均懸鏈線機制承載力也降低.

3.4? ?拆除不同樓層位置中柱框架結構承載力分析

對8層平面框架結構進行拆除中柱分析，分別拆除結構的第1層、第3層、第5層、第7層中柱，圖11顯示了各框架結構的Pushdown曲線. 圖中第X層表示8層框架結構中拆除第X層的中柱后框架結構的Pushdown曲線. 圖12給出了拆除不同樓層位置中柱框架結構梁軸力的變化情況. 拆除不同樓層中柱的框架結構對應的壓拱機制承載力和懸鏈線機制承載力計算見表2.

從圖11及表2可看出，拆除不同樓層中柱的框架結構的承載力變化規律與樓層層數不同拆除底層中柱的框架結構Pushdown曲線相似. 拆除第7層中柱后框架結構的荷載-撓度曲線表現出明顯的壓拱機制以及懸鏈線機制. 拆除其余樓層的中柱，壓拱機制并不十分明顯，且拆除中柱所在層數越低，壓拱機制越不明顯. 隨著拆除中柱所在層數的逐漸降低，框架結構的壓拱機制承載力和懸鏈線機制承載力也逐漸減小.

3.5? ?空腹梁作用

圖10以及圖12顯示了框架梁在整個Pushdown過程中梁軸力的變化情況，在壓拱機制階段（位移不大于400 mm），頂層梁和緊挨移除柱的上層梁軸力均為壓力;進入懸鏈線階段（位移大于900 mm）后，頂層梁軸力仍保持為壓力，而緊挨移除柱的上層梁軸力由受壓轉化為受拉. 中間各層框架梁內力在一個較小的范圍內隨位移變化而波動. 移除柱的上兩層梁的軸力始終為拉力，臨近破壞時增長稍快. 移除柱的框架部分的空腹梁作用表現為：頂層和緊挨移除柱的上層梁相當于空腹梁的受壓區和受拉區，中間各層接近中性軸. 空腹作用實際上也反映了樓層間的軸力傳遞的滯后效應，當緊挨移除柱上層梁處于懸鏈線受拉狀態但不發生鋼筋拉斷破壞時，隨著加載的持續進行，軸拉力逐漸地向上傳遞.空腹作用的兩大特點：1）梁端存在相對垂直位移;2）梁柱存在雙曲率變形. 空腹作用被認為移柱后框架結構進行荷載重新分布的主要機制之一.[5-6] 即，連接移柱處節點與相鄰支承點的梁產生了雙曲率變形，從而形成足夠的剪切力導致荷載重新分配. 荷載重新分布的兩個表現，一個是框架梁的彎曲軸力的改變;另一個是柱荷載通過空腹框架的作用轉移到遠離受損區域的框架柱上.

圖10以及圖12給出的各框架梁軸力變化很好地說明了移柱后框架結構連續倒塌的機制. 按照本文的分析結果，多層框架結構任意一層的中柱移除后，最可能破壞的樓層就是緊靠移除柱的上層梁. 若該梁能夠有效地發揮替換的荷載路徑作用，則不會發生連續倒塌，否則，框架結構可能發生由下而上的逐層連續倒塌.

4? ?損傷結構可靠度分析

基于上述對鋼筋混凝土平面框架的Pushdown分析，對比不同層數框架結構的空腹梁作用，發現框架結構中柱移除后，緊靠該柱的上層梁結構將是結構的重要構件. 但從可靠度角度出發，除該層框架梁結構可能發生破壞外，其他層框架梁結構也有可能發生破壞而引起結構倒塌. 基于此，本文從可靠度方面對框架結構進行進一步分析，并提出以下

假定：

1）本文計算偶然事件發生后損傷結構的條件失效概率，不考慮偶然荷載作用出現的概率.

2）損傷結構后續破壞只發生在框架梁上，不考慮相鄰框架柱的失效概率. 這是因為一般情況下，合理的設計使結構在地震作用下呈現出強柱弱梁的失效模式，柱的失效概率遠小于梁的失效概率.

3）移柱后框架結構層與層之間為串聯體系，即若某一層發生破壞喪失承載能力，則視為整個框架結構發生破壞.

4）框架結構各樓層的材料強度、構件尺寸等隨機變量的分布為獨立同分布.

5）框架結構各樓層之間的相關性為確定性相關，采用與結構受力性能相關的系數對結構各樓層荷載效應進行調整.

4.1? ?極限狀態方程對于每層框架梁，按照單層固支梁塑性計算模式建立極限狀態方程：式中：抗力R為按照固支梁計算的塑性機制承載力;C為考慮框架整體性能后（壓拱機制和懸鏈線機制等）的承載力放大系數;α為層間相關系數;作用效應S為結構的荷載作用.承載力放大系數為有限元分析后得到的確定性參數，為了確定承載力放大系數C，取：式中：Pp為按照固支梁計算的塑性機制承載力;Pa、Pu分別為通過Pushdown分析得到的框架結構壓拱機制和懸鏈線機制承載力模擬值.放大系數C通過Pushdown曲線得到的承載力進行計算，一方面體現了框架作用的整體效應，通過結構承載力的相對大小體現樓層層數的影響;另一方面考慮對比了壓拱機制承載力以及懸鏈線機制承載力的大小. 在本文有限元模擬中，將結構的失效準則確定為：拆除柱所在支承節點的豎向位移達到與節點連接的最短梁跨度18%，即0.18l. 放大系數C 的計算結果見表3.

4.2? ?相關性假定

通過Pushdown分析，得到了移柱后損傷結構各層軸力的對比圖. 由于空腹作用的影響，框架結構層與層之間發生了荷載的重新分布，軸力的相對大小能明顯體現出荷載重新分布的規律. 在懸鏈線階段，底層框架梁軸拉力最大，是引發連續倒塌最薄弱的環節;頂層框架梁承受軸向壓力，沒有達到全截面受拉的狀態，最不容易發生破壞. 從宏觀上看軸力的相對大小可體現結構發生破壞概率的相對大小. 但結構進入懸鏈線階段后，結構發生破壞與否取決于鋼筋的強度及伸長率，軸力本身對結構破壞與否并不是決定性因素. 比較而言鋼筋的應力和應變狀態能更為直觀地比較各層框架梁破壞概率的相對大小. 因此本文將通過鋼筋應變的相對大小確定框架結構樓層之間破壞概率的相關性，通過相關性系數對結構各樓層的荷載作用進行調整.

通過本文建立的OpenSees有限元模型計算，可得到不同層數框架各樓層框架梁跨中底部鋼筋應變情況. 當拆除柱所在支承節點的豎向位移達到極限位移0.18l（1.44 m）時，框架結構中底層梁縱向受拉鋼筋最大應變為0.154 4，其他各框架的各層梁相應部位受拉鋼筋拉應變的最小值為0.149 6，結構底層框架梁受拉鋼筋應變與其他層框架梁受拉鋼筋應變相差約3%. 以8層框架結構為例，頂層鋼筋拉應變為0.149 6，7層鋼筋拉應變為0.149 7，其他各層受拉鋼筋應變差值的數量級為10-4，相對差值小于1‰. 因此本文忽略這種差別，不做詳細區分，對除底層以外的其他層框架梁底部受拉鋼筋應變統一按照頂層框架梁底部受拉鋼筋應變進行結果輸出，用于后續計算，各框架梁鋼筋應變見表4.

從受力機理分析，框架梁中鋼筋拉應變的產生主要來自于兩個方面，一是移柱后損傷結構由于空腹梁作用在豎向荷載作用下產生雙曲率變形，跨中部位的彎曲變形使得框架梁底部鋼筋產生很大的拉應變;另一方面則是因為框架梁中產生的軸向力對鋼筋作用，底層梁的受壓區混凝土壓碎后，鋼筋承擔的拉力使梁截面處于偏心受拉狀態，這也是底層框架梁和其他層框架梁鋼筋拉應變差異的主要原因. 因此通過鋼筋拉應變的相對大小能有效地反映框架梁發生破壞概率的相對大小.

為了簡化計算，同時又考慮框架結構底層和其他樓層的差異，假設鋼筋應變與外荷載之間的關系為線性相關. 因此對本文計算的各個框架，以底層框架梁作為基準，底層相關性系數α1=1，其余各樓層的相關性系數αi （1

4.3? ?隨機變量分布及荷載組合效應

抗力R為固支梁塑性機制承載力，其影響因素包括：材料性能、構件幾何尺寸以及計算模型. 抗力R作為隨機變量，各因素均存在一定的不確定性，對本文模型按照《建筑結構設計統一標準》[18]查取材料、尺寸及計算模型相關參數.

荷載作用按照其分布特點可分為兩大類：一類是永久荷載即恒載，其服從正態分布;另一類是可變荷載及樓面活荷載（本文不考慮風荷載），包括持續性活荷載和臨時性活荷載，均服從極值I分布. 規范[18]規定：樓面活荷載由任意時點持續性活荷載與設計基準期最大臨時性活荷載相組合. 本文按照住宅樓面活荷載進行計算分析，荷載參數按照《建筑結構設計統一標準》查取.

對柱移除后的剩余結構進行條件失效概率分析，按照偶然組合的效應規則進行組合：

式中：ψ f1為第一個可變荷載的頻遇值系數，按照規范[19]取值.

4.4? ?結構條件失效概率

采用Monte-Carlo方法對基本抗力變量和荷載變量進行隨機抽樣（2×109次），計算單層框架梁失效概率及可靠度指標. 結構為串聯體系，則結構體系條件失效概率為p = 1-∏n1（1 - pi），pi為底層中柱移除后第i層框架梁的失效概率，則單層梁及體系失效概率計算結果見表5.

從以上計算結果可看出，隨著樓層的增加，移柱后框架結構失效概率增大，結構體系可靠度逐漸減小. 一個原因是移柱位置框架梁受力特征隨上部樓層增加而變化：從圖10（e）各框架底層軸力對比圖可看出，結構在達到極限位移0.18l（1.44 m）時，底層框架梁軸拉力因空腹作用而隨著樓層層數的增加而增大，因此框架結構達到相同的極限位移條件下，8層框架底層梁更容易出現鋼筋拉斷而發生結構破壞. 另一原因則是移柱后框架結構各層梁之間的受力接近串聯體系，隨著樓層層數的增加，任意樓層的失效都將導致結構體系失效，從而使得結構體系失效概率相應增大.

5? ?結? ?論

1）本文采用OpenSees軟件建立有限元分析模型，對鋼筋混凝土約束梁、單層框架結構和多層框架結構連續倒塌試驗進行數值模擬，利用試驗獲取的豎向位移和水平位移數據驗證本文所建立的有限元模型，結果表明數值模擬結果與試驗結果吻合良好. 說明本文的有限元模型能夠較好地模擬平面框架結構抗連續倒塌過程中的壓拱機制、轉換機制和懸鏈線機制.

2）通過非線性靜力Pushdown分析方法對不同層數的移柱后框架結構進行分析，研究了樓層層數對移柱后框架結構抵抗連續倒塌能力的影響. 發現隨著樓層層數的增加，壓拱機制和懸鏈線機制承載力均有所降低.

3）移柱后損傷框架在荷載作用下將形成空腹梁作用，頂層框架梁和緊靠移除柱的上層框架梁相當于空腹梁的受壓區和受拉區，中間各層接近中性軸. 空腹梁作用造成框架梁軸力的改變，緊靠移除柱的上層梁結構成為結構的重要構件. 若該梁能有效地發揮替換的荷載路徑作用，則結構不會發生連續倒塌.

4）本文采用數值模擬與理論分析結合的方法，提出一種新的計算損傷框架體系可靠度的辦法. 對移柱后損傷框架建立單層框架梁連續倒塌極限狀態方程，在方程中比較壓拱機制與極限狀態懸鏈線機制的承載力，設定承載力放大系數，并考慮影響連續倒塌的各個因素;采用串聯體系計算體系條件失效概率，選取鋼筋應變作為樓層相關性系數對結構各樓層荷載效應進行調整.