基于LFM信號的TDMA網絡精密時間同步方法

王天雄，陳仕進，張玉鵬，閆勝虎

(中國電子科技集團公司第五十四研究所，河北 石家莊 050081)

0 引言

時間同步是時分多址(TDMA)網絡正常運行的基礎，網內各個節點的時間同步精度達到微秒量級，即可保證節點間的無碰撞同步信息傳輸，常用的時間同步算法均能滿足需求，例如：參考廣播方法[1]、RTT時間同步算法[2-3]和PTP時間同步算法[4]。文獻[5-6]針對自組織網絡研究了分布式同步算法，雖然時間同步精度不高，但是無需中心節點，網絡抗毀性能高。若要利用TDMA數據鏈路進行節點間的測距，則需要提高網內時間同步精度，例如：30 m的測距誤差就要求時間同步精度達到100 ns以內。為了提高時間同步精度，文獻[7]設計了基于卡爾曼濾波的高精度RTT時間同步算法，將時間同步誤差控制在50 ns以下。文獻[8]將卡爾曼濾波和RTT-PTP算法相結合，在Link22數據鏈結構的基礎上降低了時間偏差率誤差。

隨著多戰斗單元協同作戰理論和體系的發展，數據鏈路的時間同步面臨著更嚴峻的挑戰。例如：戰斗單元執行協同探測、協同偵查等任務時需要各個戰斗單元間納秒級的時間同步[9-11]，而衛星導航信號一旦被干擾，外部時鐘源無法進行授時，這就需要靠數據鏈路完成納秒級的精密時間同步，為其他作戰載荷提供時統，支撐協同作戰任務。

本文通過研究TDMA網絡的RTT同步技術，分析同步誤差產生的原因。設計了基于線性調頻(LFM)脈沖的時間同步算法，利用LFM脈沖壓縮的抗多普勒優勢[12-13]，通過采用大時間帶寬積的LFM脈沖提高了時隙到達時間的估計精度。仿真和實際平臺驗證表明該算法行之有效。

1 RTT同步技術

RTT時間同步方法是通過測量網絡內節點之間的信號往返時間來估計時間同步誤差的。在估計時間誤差的同時，還能夠估計出節點間的信號傳輸時延，因此，常用于TDMA網絡的節點間測距。

RTT時間同步原理如圖1所示。其中，tm為主節點(時鐘參考節點)時間，tc為從節點時間，Δt為主從節點的時鐘誤差。通過RTT算法可以將時間tc與時間tm同步。

圖1 RTT時間同步原理

從節點在其本地時間tc1時發送RTT詢問時隙，主節點在其本地時間tm1時收到來自從節點的RTT詢問時隙，時隙傳輸時延為tp1。主節點在其本地時間tm2發送RTT應答時隙，從節點在其本地時間tc2時收到來自主節點的RTT應答時隙，時隙傳輸時延為tp2。

假設主從節點交互時隙的時間非常短，主從節點間的距離可以近似認為不變，即可以取tp1=tp2=tp，此時，以上各參數滿足以下方程：

(1)

從而有：

Δt=(tm1+tm2-tc1-tc2)/2，

(2)

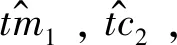
(3)

分析上述RTT時間誤差估計流程可以看出，在不考慮硬件一致性等原因引起的系統誤差的前提下，僅從算法本身考慮，主要存在以下估計誤差：在估計tm1，tc2的時候存在估計誤差εm，εs；由主從節點的時鐘相對漂移引入的隨機誤差εc；主從節點交互脈沖時由于主從節點的相對位置變化會引起tp1≠tp2，因此會造成產生估計誤差εtp。

目前減小上述誤差的途徑主要有3條：在硬件上提高用作系統時鐘的晶振穩定度，減小εc的方差；在軟件上使用卡爾曼濾波等估計算法，減小由εc，εm，εs引起的估計誤差方差；在幀結構設計上，盡量減小主從節點的時隙交互時間，減小由εtp引起的估計誤差。

然而，由于εm，εs的方差較大，即使采用了相應的估計算法，時間同步誤差也只能控制在幾十納秒量級。要想進一步提高時間同步精度，需要從根本上減小εm，εs的方差。當信號帶寬受限時，增加信號持續時間、提高信號的時間帶寬積是提高信號到達時間估計精度的有效手段。對于常規的偽隨機序列調制信號，提高信號持續時間就意味著增加序列碼長。但在多普勒頻偏條件下，對偽隨機序列進行長碼匹配濾波，其累積能量損失會隨著其碼長的增加而增大，累積能量信噪比的降低直接影響信號的捕獲概率和到達時間的估計準確度[14-16]。若采用差分能量累積算法，則會額外損失信噪比，要想達到與相干能量累積相同的效果，需要進一步加長偽隨機序列，增加額外時間開銷。若采用分段匹配加FFT的能量累積算法，額外信噪比損失較小，但會大大增加系統的復雜度，且原有的時域一維峰值搜索將變為時頻二維峰值搜索，增加了算法的復雜度。因此，采用偽隨機長碼序列調制信號進行信號到達時間估計存在很大的局限性。

線性調頻信號(LFM)對多普勒頻偏有天然的抗性，文獻[17-18]指出，通過脈沖壓縮方法對LFM信號進行能量累積時，由多普勒頻偏引起的能量損失只與頻偏帶寬比有關，與信號持續時間無關。因此，可以對大時間帶寬積的LFM信號直接進行脈沖壓縮，并利用能量峰值位置準確估計脈沖到達時間，算法復雜度和實現復雜度均較低。

2 LFM信號原理

2.1 LFM信號的脈沖壓縮

線性調頻信號可以表示為：

(4)

式中，A為幅度，f0為初始頻率，k為調頻率。設線性調頻信號的持續時間為τ，其理想的時頻分布如圖2所示。

圖2 線性調頻信號的理想時頻分布

從圖2中能夠看出，線性調頻信號的時寬為T=τ，其頻率隨時間線性變化，因此是非平穩信號，其瞬時頻率為：

f=f0+kt。

(5)

脈沖壓縮是雷達術語，在通信領域，即為匹配濾波。因此，LFM脈沖的捕獲和到達時間估計，是通過搜索信號匹配濾波響應峰值來實現的[12]。

2.2 LFM信號脈壓抗多普勒原理

線性調頻信號對多普勒頻移不敏感，在較大多普勒頻移的情況下，仍能通過匹配濾波得到很好的能量累積，但匹配濾波器響應會產生附加時延，延時的大小正比于多普勒頻移，延時會使脈沖到達時間的估計產生誤差。

LFM多普勒頻移影響示意圖如圖3所示。LFM脈沖附加了多普勒頻移之后，相對于原有頻率附加了頻率fd。實線部分為原始頻率變化范圍，虛線部分為頻移后的頻率變化范圍，因為只有頻率在f1～f2部分的波形可以通過脈沖壓縮收集能量，所以引入多普勒頻移后，將會產生以下不利影響：

① 可壓縮段變小了，將會損失一定的累積能量，損失部分可以表示為Δtd/T；

② 匹配濾波器輸出響應產生附加時延Δtd=Tfd/(f1-f2)。

圖3 LFM多普勒頻移影響示意圖

通過上述分析可知，當實際的多普勒頻移與LFM信號帶寬比較小時，產生的能量損失可以忽略不計。但產生的附加時延必需予以補償。正負斜率脈沖多普勒補償算法可以有效地修正附加時延。

正負斜率脈沖補償算法要求發送端連續發送正斜率脈沖和負斜率脈沖2個LFM脈沖，即2個脈沖信號的調頻斜率幅值相等，方向相反。在接收端需要2個匹配濾波器分別匹配正斜率脈沖和負斜率脈沖。當發射正斜率脈沖時，多普勒頻移使脈壓后的波形包絡在時間軸上發生移動，偏移量為Δtd1=-2πfd/k。同理，發射負斜率脈沖時，多普勒頻移使脈壓后的波形包絡在時間軸上發生移動，偏移量為Δtd2=2πfd/k,其原理如圖4所示。

圖4 多普勒對LFM正負斜率脈沖的影響

3 基于LFM的TDMA網絡時間同步方法

3.1 TDMA網絡幀結構

為了利用LFM脈沖進行信號到達時間估計的優勢。TDMA網絡時幀結構如圖5所示。一個時幀被分為2部分，前半部分為LFM脈沖部分，用于節點間進行信號往返時間估計，每個節點發送一個LFM脈沖串#n′，每個脈沖串包含若干個正負斜率脈沖對；后半部分為通信波形部分，用于節點間進行正常通信和傳輸LFM脈沖串到達時間的估計結果。

圖5 系統時幀結構圖

將LFM脈沖集中設計在時幀的前區，是為了盡可能地減小節點間信號往返交互的時間，從而減小誤差εtp的影響。

3.2 TDMA網絡時間同步流程

基于上述時幀結構，主從節點工作流程如圖6所示。

圖6 主從節點工作流程

主節點流程描述為：

① 系統初始化后，在tm=0時產生幀起始脈沖，為通信時隙和LFM脈沖時隙提供時間基準；

③ 在tm為tm2時發送RTT應答脈沖串；

由于LFM脈沖串本身沒有調制信息，因此，從LFM信號本身無法區分脈沖的信源，所以，在主從節點時間不同步時，從節點無法辨認主節點發送的LFM脈沖串，也就無法進行時間的初始化校準。為了克服上述問題，從節點借助通信時隙來完成時間的初始化校準，因此，從節點的時間同步分為時間粗同步和時間細同步2個步驟。

在時間粗同步階段，從節點工作流程描述為：

① 系統初始化后從節點保持靜默，接收主節點通信時隙，從中恢復時間的粗定時；

② 在粗同步的時間下，根據脈沖串到達時間區分脈沖串的信源，并進行本節點各LFM脈沖時隙和通信時隙的發送。

在時間細同步階段，從節點工作流程描述為：

① 在tc=0時產生幀起始脈沖，為通信時隙和LFM脈沖調制提供時間基準；

② 在tc為tc1時發送RTT詢問脈沖串；

⑤ 按式(3)計算Δt，并修正本地時間；

4 仿真和實現驗證

本文針對上述TDMA網絡時間同步方法，以4節點網絡進行了仿真和實現驗證。

仿真條件1：校時幀周期為40 ms，其中LFM脈沖部分占3 ms，通信波形部分占37 ms，每個LFM脈沖串包含8個正負斜率脈沖對，每個脈沖脈寬40 μs；信號帶寬20 MHz；多普勒頻偏20 kHz；系統時鐘晶振穩定度10-8；節點相對運動速度不大于30 m/s。主從節點的時間同步誤差如圖7所示。

圖7 條件1下主從節點的同步誤差圖

從圖7可以看出，在接收信噪比達到-14 dB時，時間同步誤差開始收斂，當信噪比達到-8 dB時，同步誤差標準差不大于5.5 ns。

仿真條件2：在條件1的基礎上分別將LFM脈沖帶寬和脈沖寬度降低到10 MHz，20 μs，仿真結果如圖8所示。從圖8可以看出，由于降低LFM的帶寬或脈寬減小了脈沖的時間帶寬積，致使時間同步靈敏度下降，-8 dB時，時間同步誤差標準差增大到10 ns左右。

仿真條件3：在仿真條件1的基礎上將多普勒頻偏增加到200 kHz，仿真結果如圖9所示。

圖8 條件2下主從節點時間同步誤差圖

圖9 條件3下主從節點時間同步誤差圖

比較圖7和圖9可知，LFM信號具有良好的抗多普勒性能，在200 kHz多普勒頻偏下，時間同步靈敏度和時間同步精度均未有明顯的損失。

仿真條件4：在條件1的基礎上分別將時鐘穩定度調制為10-7，節點間相對運動速度調整為300 m/s，校時幀周期調整為1 s，仿真結果如圖10所示。

圖10 條件4下主從節點時間同步誤差圖

從圖10可以看出，時鐘穩定度、相對運動速度和校時幀周期直接影響時間同步精度，為了減小時間同步精度損失，應選用高穩定度的時鐘和減小校時周期。

根據上述方法設計FPGA程序實現，并加載到現有的通信終端設備上，實驗條件是仿真條件1的基礎上去掉節點間的相對運動速度，利用示波器來觀察實際的主從節點幀起始脈沖的同步情況。

實驗結果顯示，從節點的幀起始脈沖在主節點幀起始脈沖附近波動，誤差介于±4 ns左右之間，因為沒有模擬節點間的相對運動，所以實測結果要好于仿真結果。

5 結束語

本文利用LFM信號抗多普勒性能強的特點，基于LFM信號設計了TDMA網絡的RTT時間同步算法。LFM信號的高時間帶寬積提高了接收端脈沖壓縮的能量累積量，減小了脈沖到達時間的估計誤差；節點間集中交互LFM脈沖的幀結構，減小了脈沖交互時間，降低了節點間相對運動引入的時間同步誤差。仿真和實際平臺驗證結果表明，該方法在大多普勒頻移環境下仍能夠大幅提高TDMA網絡內節點的時間同步精度，可以為其他任務載荷提供高精度授時，特別適用于小規模協同作戰。