射頻接收機中自動增益控制電路建模與設計

王 帥，張 杰，張彥峰

(中國電子科技集團公司第五十四研究所，河北 石家莊 050081)

0 引言

在無線通信中，由于受距離遠近、電磁波輻射功率大小及氣象條件等各種因素影響，射頻接收機接收到的射頻信號功率強度動態范圍較大。為了保證接收機輸出信號強度和信號質量，接收機需要AGC電路[1-2]。

在實際電路應用中，一般要求AGC電路的增益調整時間恒定，與接收到的信號功率大小無關，與設置的穩定輸出功率值無關。同時，時分通信體制要求射頻接收機具有較小的AGC穩定時間，而QPSK等信號調制體制要求射頻接收機具有較大的AGC穩定時間[3-5]。因此，AGC電路增益調整時間的長短十分關鍵。

1 AGC環路分析

射頻接收機兼容QPSK和時分體制，要求該接收機AGC穩定時間(AGC時間常數是穩定到63.2%所需時間，AGC穩定時間一般是幾倍的時間常數)在35～40 μs，傳統的設計方法是根據經驗值進行初值電裝，再根據測試結果不斷修正再測試，拓撲結構不合適則需要重新投板再加工，缺乏準確的理論設計和仿真設計。

典型的AGC電路原理框圖如圖1所示，一般由可變增益放大器(VGA)、檢波器、比較電路和環路濾波電路組成[6-7]。檢波電壓經過與基準電壓的比較和環路濾波，產生的控制電壓調整可變增益放大器增益，使輸出信號電平在較小的范圍內波動。

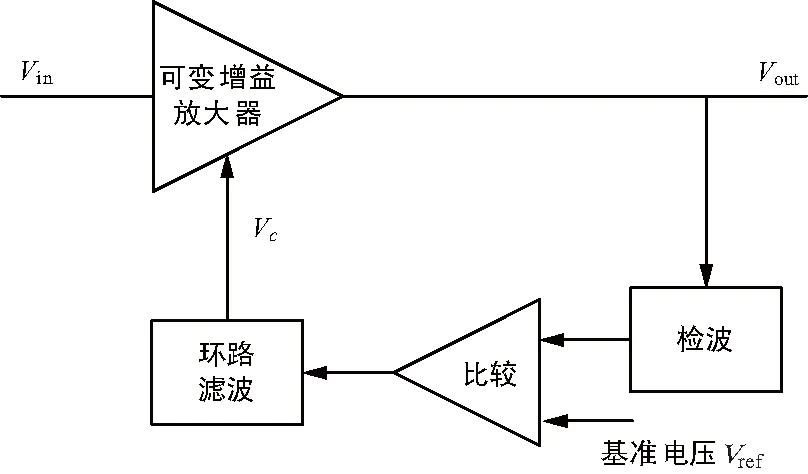
圖1 AGC電路原理框圖

AGC電路的優點是具有優秀的線性特性且電路實現不需要大動態范圍的檢波器；缺點是存在一定的不穩定性，即為了保持穩定性限定了最大的環路濾波帶寬，限定的最大環路濾波帶寬限制了最小的AGC電路時間常數。Vout和Vin分別是輸入輸出信號的幅度，G(Vc)是受電壓Vc控制的可變增益放大器增益[8]，則:

Vout=Vin·G(Vc)。

(1)

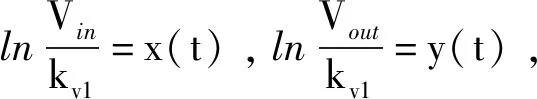
y(t)=x(t)+ln(G(Vc))。

(2)

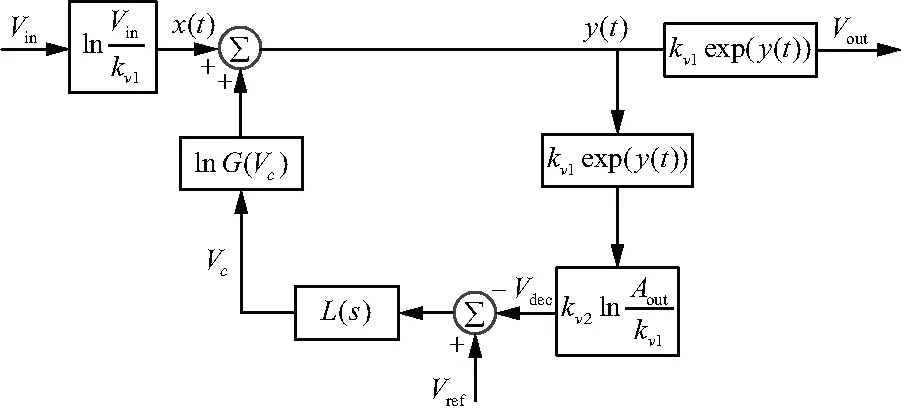
圖2 自動增益控制環路模型

可變增益放大器的增益控制電壓為：

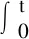
(3)

對式(2)兩邊求導，并把式(3)代入，得到:

(4)

假如L(s)和比較電路用圖3所示電路來實現，本文稱其為RC比較環路濾波電路。

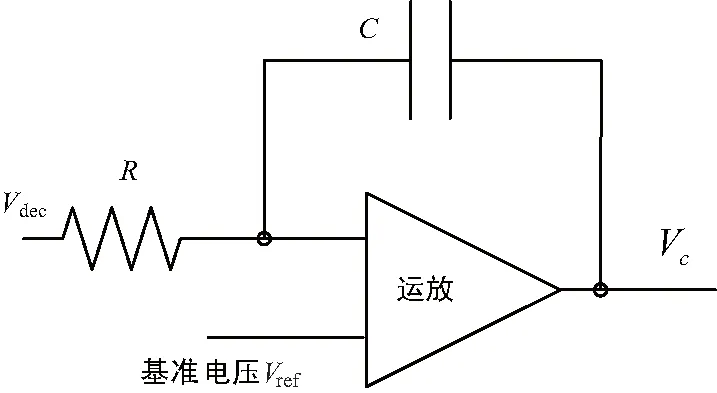
圖3 RC比較環路濾波電路

根據圖3可以推導出：

(5)

結合式(3)～式(5)得到：

(6)

(7)

時間常數為：

(8)

G(Vc)=k1ekVc，

(9)

式中，k1為常數，所以要求可變增益放大器的增益與控制電壓成指數關系，即增益的對數跟控制電壓成線性關系，可以實現AGC時間常數恒定的要求[10-11]。

2 AGC電路建模

根據上節論述得到了AGC電路恒定時間常數的要求，但仍然缺少復雜AGC電路時間常數的詳細公式，沒有解決特定AGC時間常數的設計難題。本文對實際射頻接收機AGC電路進行建模，模型如圖4所示。

該模型不同于圖2的模型，圖2的模型是基于電壓進行建模運算，雖然進行了對數轉換，但仍然不夠直觀。圖4的模型直接采用實際接收機接收功率進行建模運算[12-14]，該模型的Pin，Pout分別代表AGC電路的輸入功率和輸出功率，量值為dBm；GdB(Vc)表示可變增益放大器的增益與控制電壓的對數關系，表達式為GdB(Vc)=kg·Vc，kg是可變增益放大器對數增益與控制電壓的線性斜率，單位為dB/V,該可變增益放大器的特性符合上節的AGC電路恒定時間常數的限定要求。D(Pout)表征檢波電壓與輸出功率成對數關系，表達式為D(Pout)=kd·Pout，kd是檢波器電壓與輸出功率的線性斜率，單位為V/dBm。H(s)和C(s)表征AGC電路中比較和環路濾波電路的實際數學建模。因此得到式(10)～式(13)。

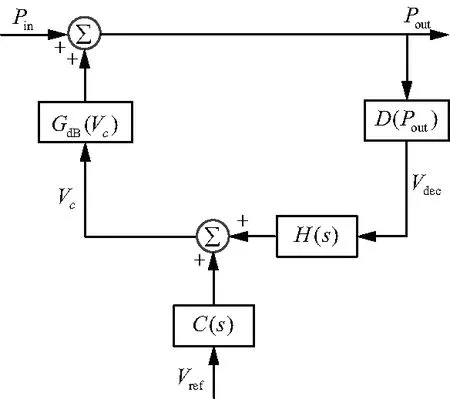
圖4 射頻接收機AGC電路模型

(10)

Vc=H(s)Vdec+C(s)Vref，

(11)

Pout=Pin+kg(kdH(s)Pout+C(s)Vref)，

(12)

(13)

(14)

(15)

根據式(13)可知，Pout為Pin和Vref經過各自閉環傳遞函數線性疊加的結果，即式(14)～式(15)。對于一個實際AGC電路，Vref為固定值，根據上一節知道，圖4配置模型的AGC時間常數與Vref無關。因此對于圖4模型的AGC時間常數只需要分析式(14)，而式(15)影響最后的收斂穩定值。

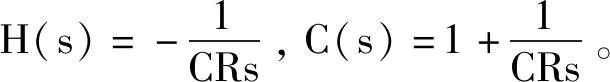
(16)

根據式(14)得到Pout1的閉環傳遞函數為：

(17)

圖4類型的AGC電路時間常數為式(18)，與式(8)相吻合。

(18)

根據式(18)可知圖4類型的AGC電路時間常數與該電路的電容C容值、電阻R阻值成正比，與可變增益放大器增益斜率和檢波斜率成反比。

當一個AGC電路可變增益放大器和檢波芯片已經確定，則影響AGC時間常數的主要因素就是比較環路濾波電路。下面針對另外2種射頻接收機常用的AGC電路進行AGC時間常數公式推導，圖5是一種較為常用的比較環路濾波電路(本文稱為常用一階比較環路濾波電路)，對該電路采用本文論述的方法進行分析，得到閉環傳遞函數式(19)，該拓撲結構的時間常數公式為式(20)，根據公式知道AGC電路的時間常數與電容容值成正比，與R1和R2阻值正相關，與可變增益放大器增益斜率和檢波斜率成反相關。

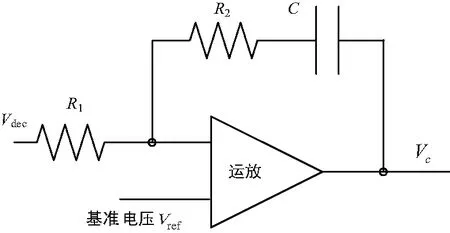
圖5 常用一階比較環路濾波電路

(19)

(20)

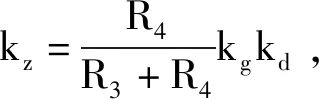
(21)

(22)

(23)

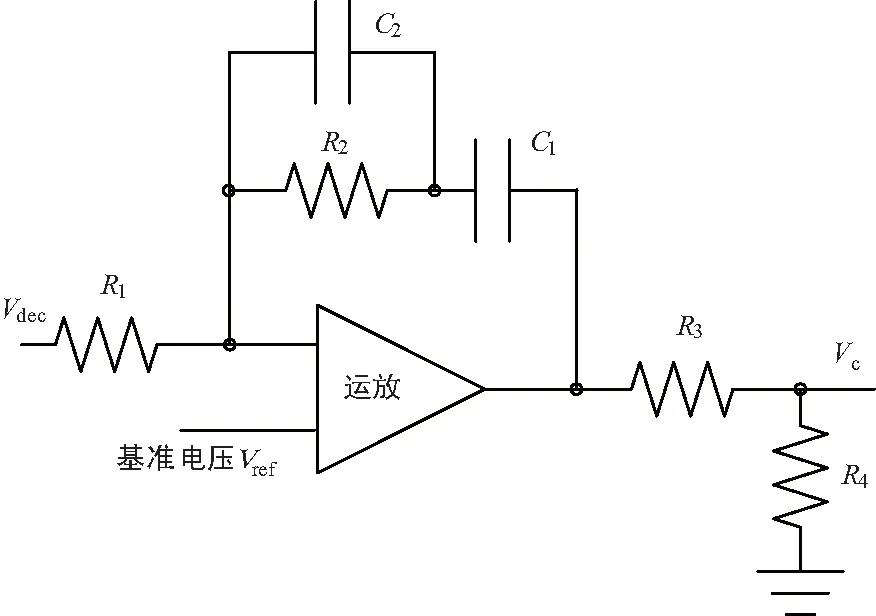
圖6 常用二階比較環路濾波電路

3 仿真驗證和電路驗證

上節對射頻接收機的AGC電路進行了具體建模，對3種常見的比較環路濾波電路進行了AGC時間常數公式推導，得到了具體的表達式。本節采用電子設計軟件進行建模仿真，仿真結果與上節的公式結論進行對比驗證，對常用二階比較環路濾波電路進行加工制作，測試其AGC穩定時間。

采用Keysight公司的Advanced Design System(ADS)軟件對接收機的AGC電路進行建模仿真，仿真原理圖如圖7所示，該仿真針對的是RC比較環路濾波電路[15]。模型中采用兩級可變增益放大器來保證AGC電路的動態范圍，增益斜率為100 dB/V，檢波器的檢波斜率為0.05 V/dB,在原理圖中對AMP6的VoltSlope參數進行了合適設置使其匹配實際檢波器斜率[16-18]。因此kg=100 dB/V，kd=0.05 V/dB，R=40 kΩ，C=100 nF，根據式(18)計算得到時間常數為0.8 ms(穩定到63.2%)，假設穩定到86.5%為整個AGC電路的穩定時間，那么穩定時間為2倍時間常數，即為1.6 ms。ADS仿真結果如圖8所示，根據仿真數據分析得到向下恢復時間常數為0.809 ms，穩定時間為1.617 ms；向上恢復時間常數為0.807 ms，穩定時間為1.616 ms;與模型公式理論計算結果吻合很好。

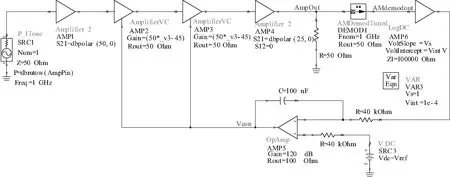
圖7 ADS軟件下AGC電路仿真原理圖

對圖5模型(常用一階比較環路濾波電路)進行ADS軟件仿真，可變增益放大器參數和檢波器參數同圖7一致，其他參數為R1=39 kΩ，R2=30 kΩ，C=100 nF；圖6模型(常用二階比較環路濾波電路)相應參數為R1=10 kΩ，R2=10 kΩ，R3=39 kΩ，R4=10 kΩ，C1=1 nF，C2=16 pF。按照式(20)可以計算出常用一階比較環路濾波電路模型在該參數下的時間常數為3.78 ms；而采用ADS軟件對其進行仿真得到下降恢復時間常數為3.82 ms，上升恢復時間常數為3.74 ms。按照式(23)計算出常用二階比較環路濾波電路模型在該參數下無阻尼自然振蕩角頻率為790 570 rad/s,阻尼系數為7.97。因為阻尼系數大于1，該拓撲為過阻尼，極點

閉環極點p2比p1距虛軸遠得多，故忽略p2對輸出的影響，把二階系統近似作為一階系統來處理，因此，時間常數計算為τ3=-1/p1=20 μs；采用ADS軟件對其電路結構進行仿真，得到下降恢復時間常數為19 μs，上升恢復時間常數為19 μs。3種電路結構模型理論計算和ADS軟件仿真結果對比如表1所示。

表1 AGC時間常數理論計算和ADS仿真對比

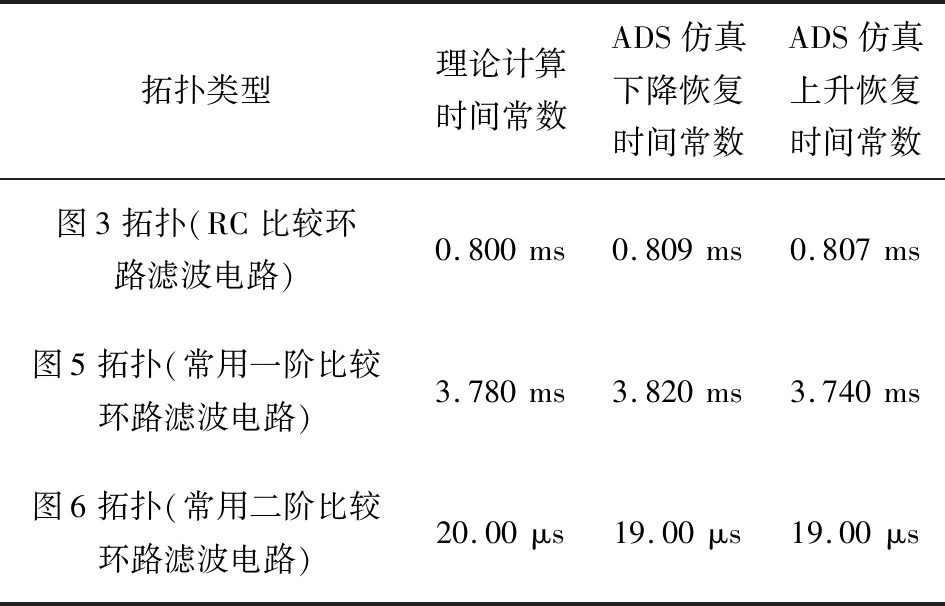
拓撲類型理論計算時間常數ADS仿真下降恢復時間常數ADS仿真上升恢復時間常數圖3拓撲(RC比較環路濾波電路)0.800ms0.809ms0.807ms圖5拓撲(常用一階比較環路濾波電路)3.780ms3.820ms3.740ms圖6拓撲(常用二階比較環路濾波電路)20.00μs19.00μs19.00μs

該射頻接收機實際要求AGC穩定時間為35～40 μs，采用常用二階比較環路濾波電路的拓撲結構和舉例的各個電阻和電容參數進行實際電路制作，圖9為加工電裝后的實際電路，該電路的AGC時間常數理論計算為20 μs，ADS仿真結果為19 μs，各自達到穩定時間(86.5%穩定)分別為40,38 μs。實際測試結果如圖10所示，AGC穩定時間為36.8 μs，與理論計算和軟件仿真結果吻合良好，滿足實際系統要求。

圖9 接收機中的AGC電路

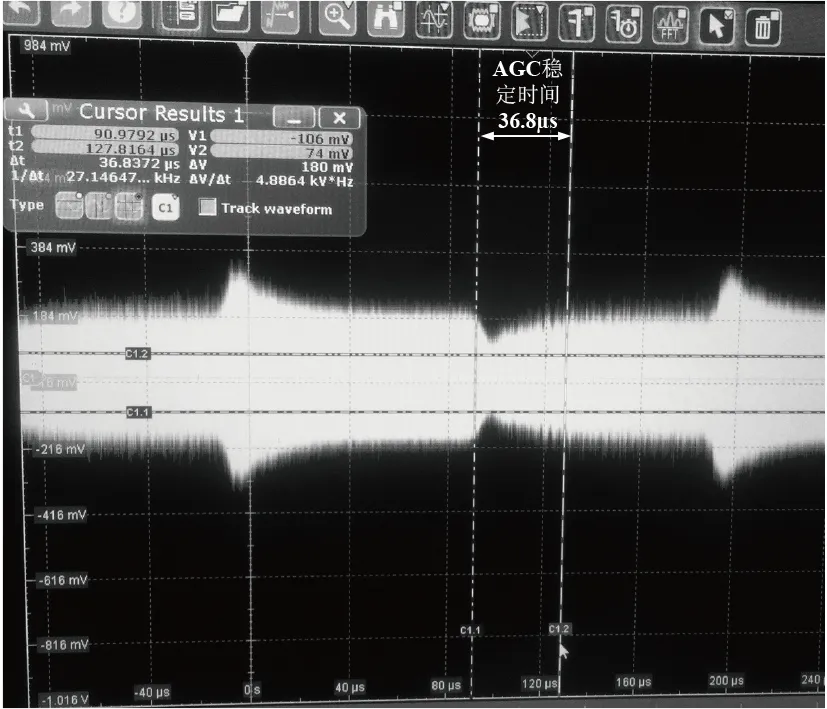
圖10 示波器測試結果

4 結束語

本文對射頻接收機中自動增益控制電路進行了建模分析，得到了穩定時間常數的電路條件。在此基礎上提出了射頻接收機中自動增益控制電路的物理模型，對于3種常見自動增益控制電路進行了時間常數公式推導和ADS電子設計軟件仿真驗證，而且進行了實際射頻接收機電路制作和測試，理論計算結果、軟件仿真結果和實際電路測試結果吻合良好，證明了模型的準確性和軟件仿真的可行性。對于特定AGC時間常數的自動增益控制電路設計，采用本文的公式和方法可以準確計算出該AGC電路的時間常數，利用ADS電子設計軟件繼續對電路參數進行仿真優化直到滿足系統需求的AGC時間，節約了后期大量的調試時間，本文的設計方法對AGC電路設計有很好的理論指導作用。