一種基于應力-應變特征的巖石脆性指數評價改進方法

曹 茜 ，戚明輝 ，張昊天 ，黃 毅 ，張燁毓

（1.頁巖氣評價與開采四川省重點實驗室，成都 610091；2.四川省科源工程技術測試中心，成都 610091；3.成都理工大學油氣藏地質及開發工程國家重點實驗室，成都 610059）

0 引言

脆性是巖石綜合力學性質的一種表現，與巖石的礦物組成、成巖作用及應力狀態等因素均有關［1-5］。作為巖石的重要屬性之一，巖石脆性對油氣資源的勘探及開發起著至關重要的作用，巖石脆性評價最終可以服務于工業化壓裂施工生產方案。

目前，國內外學者研究泥巖脆性參數的方法主要有礦物組分法、彈性力學參數法及應力-應變測試法［6-12］。Jarvie 等［10］在對 Barnett儲層產氣量較高層段的巖石樣品進行研究的過程中，提出利用（石英+碳酸鹽）含量/礦物總量計算其脆性指數，在此基礎上張晨晨等［13］和 Cao 等［14］分別考慮樣品的總有機碳（TOC）含量和鏡質體反射率（Ro）對該方法進行了改進。從本質上看礦物組分法雖然可以在一定程度上表征巖石整體的脆性，然而受沉積環境等因素的影響，礦物組成相同的巖石樣品其孔隙度和密度可能均不同，從而具有不同的脆性特征。一些學者提出根據對巖石樣品進行的室內三軸壓縮實驗結果，可得到不同樣品的應變強度等力學參數，從而建立應力-應變關系曲線，進而獲取特征參數來評價巖石的脆性特征，然而脆性不是巖石的某種單一屬性，而是一種綜合的力學特征，巖石脆性也受其物質組成、結構、孔隙及流體等因素的影響［15-19］。利用楊氏模量和泊松比表征巖石脆性的理論依據是巖石樣品的應力-應變關系，即巖石在變形和破壞時存在著明顯的差異，其脆性和塑性行為也可以在全應力-應變曲線上反映出來［20-22］，因此，在巖石脆性指數評價的過程中，須綜合考慮彈性模量、泊松比、應力-應變及強度等參數的影響，這樣既能夠反映巖石在受壓時的破壞情況，又能夠反映巖石破裂后維持裂縫發展的能力。

以四川盆地新場氣田須家河組五段21塊巖石樣品的室內三軸力學實驗測試為基礎，分析應力-應變關系曲線中反映的巖石脆性特征，提出改進巖石脆性指數評價的方案，并針對實測樣品特征建立脆性指數模型，進而對模型的可靠性進行討論，以期更加準確地評價巖石的脆性特征。

1 實驗樣品及方法

1.1 實驗樣品

本次實驗樣品共計21塊（表1），均取自四川盆地新場氣田須家河組五段，對應巖性主要有黑色、灰黑色、深灰色泥巖，黑色炭質泥巖，淺灰色、灰色砂巖等，樣品的TOC質量分數主要為2%～15%，Ro主要為0.5%～2.0%，孔隙度主要為1%～4%。

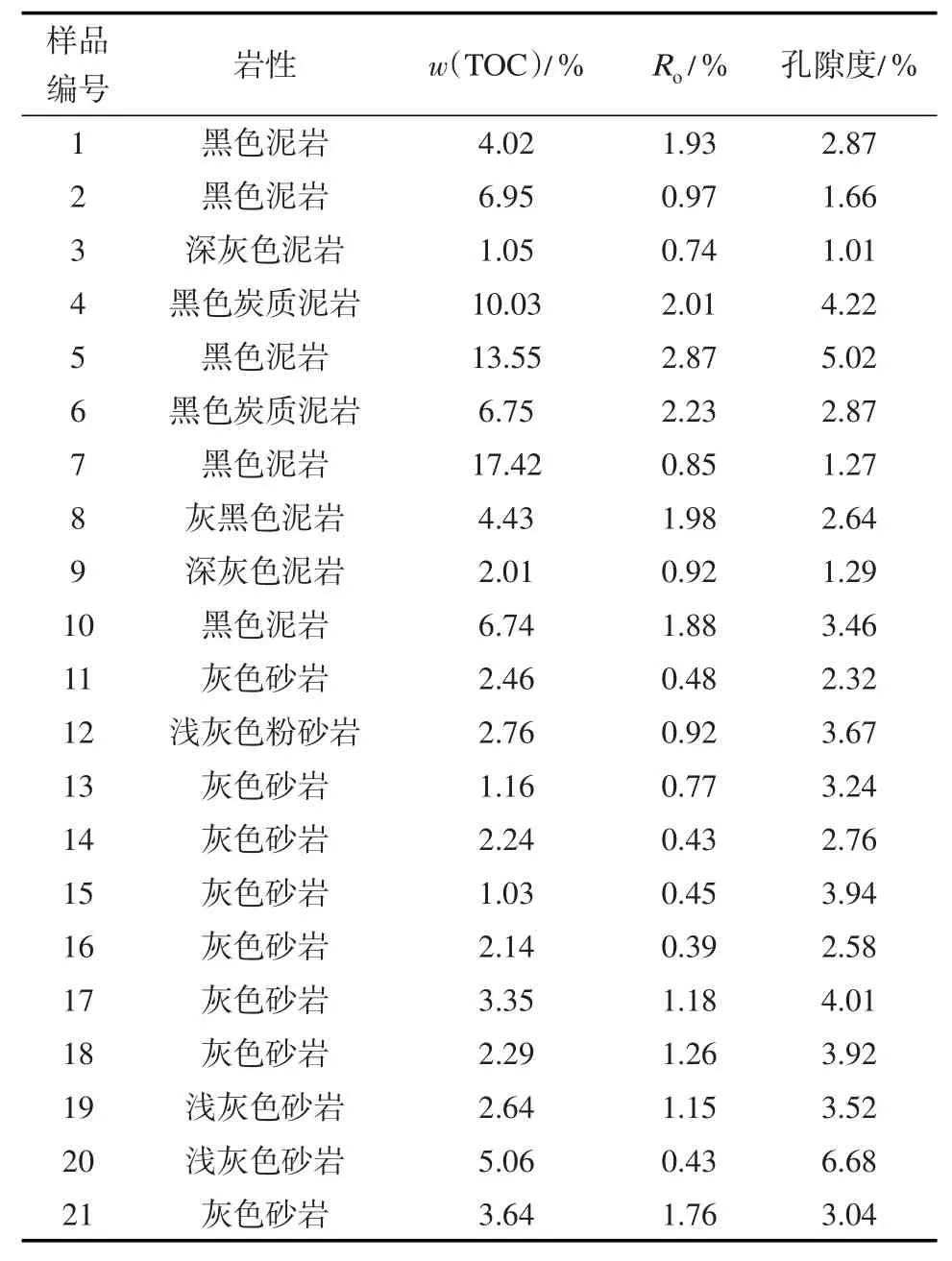
表1 巖石樣品信息Table 1 Data of rock samples

1.2 實驗方法

實驗室巖石力學特征測試是研究巖石力學性質最直接的方法，為了全面地分析巖石脆性特征，對研究區巖石樣品的物理性質、應力-應變特征及聲波特征等進行了測試。應力-應變測試所采用的儀器是從美國MTS公司引進的數字伺服程控剛性實驗機，該儀器可以在模擬測試地層條件下巖石靜力學參數的同時進行超聲波同步測試，進而獲取縱橫波速度；儀器的最高伺服軸壓為1 000 kN，圍壓為140 MPa，孔壓為70 MPa，環境溫度為200℃；孔隙流體介質飽水或飽氣。系統可在溫度、壓力（軸壓、孔壓及圍壓）變化組合條件下模擬各種地層條件，并對巖石力學參數、孔滲參數及超聲波速進行同步測試。壓力傳感器測量誤差小于1%；軸向位移傳感器量程為-50～+50 mm，位移分辨精度為0.000 1 mm；超聲波換能器對于直徑 25 mm樣品頻率為1 MHz。本次測試樣品直徑和長度分別為25 mm和50 mm。

2 測試結果

本次實驗對泥巖和砂巖樣品的巖心分別進行模擬地層條件下的三軸飽水力學和聲學測試。考慮樣品所在區域地層有效圍壓約為32 MPa，分別測試圍壓12 MPa，22 MPa，32 MPa下泥巖和砂巖的應力-應變特征以及不同圍壓和軸壓下泥巖和砂巖的縱橫波速度，在21塊樣品中對1，11，12，13號樣品測試了圍壓12 MPa下的應力-應變特征、縱橫波速度和抗壓強度，對 2，3，4，5，14，15，16 號樣品測試了圍壓22 MPa下的應力-應變特征、縱橫波速度和抗壓強度，對 6～10，17～21號樣品測試了圍壓32 MPa下的應力-應變特征、縱橫波速度和抗壓強度，測試結果如表2所列。

表2 巖石樣品脆性特征Table 2 Brittleness characteristics of rock samples

分析不同樣品抗壓強度、楊氏模量及泊松比與圍壓之間的關系表明：①巖石的抗壓強度隨圍壓的增加而增大，且砂巖的抗壓強度明顯高于泥巖的抗壓強度；隨著圍壓的增大抗壓強度的增大量降低。當圍壓為0 MPa時，所選樣品的抗壓強度均較低；當圍壓從0 MPa增加到12 MPa時，所選樣品的抗壓強度均明顯增大；當圍壓大于12 MPa時，隨著圍壓的增加，大部分巖石樣品抗壓強度增大量變小，僅有個別樣品的抗壓強度增大量較大［圖1（a）］。當圍壓一定時，砂巖的抗壓強度明顯高于泥巖；圍壓越大，砂泥巖抗壓強度在巖性上的差異越明顯。②巖石的楊氏模量隨圍壓的增加而增大，砂巖的楊氏模量高于泥巖的楊氏模量。砂泥巖的楊氏模量均隨著圍壓的增加而增大，砂巖樣品楊氏模量隨圍壓的增加明顯增大，泥巖樣品的楊氏模量隨圍壓的增加則增大量較小。在圍壓相同時，砂巖樣品的楊氏模量高于泥巖，但是部分泥巖樣品也具有較高的楊氏模量，尤其是在低圍壓（圍壓為10 MPa左右）下砂泥巖楊氏模量差異較小［圖1（b）］。③巖石的泊松比隨圍壓的增大而減小，泥巖的泊松比大于砂巖。圍壓越高，巖石的泊松比越小，17，19，20號砂巖樣品的泊松比隨圍壓增加而減小的趨勢較為明顯，1，3，5號泥巖樣品的泊松比隨圍壓變化的趨勢并不明顯。在圍壓較低時（圍壓小于12 MPa），不同樣品的泊松比差異并不明顯，隨著圍壓的升高，泥巖的泊松比變化不大，而砂巖的泊松比明顯減小，所以在高圍壓下（圍壓大于22 MPa）泥巖的泊松比要明顯高于砂巖的泊松比［圖1（c）］。

圖1 巖石抗壓強度（a）、楊氏模量（b）、泊松比（c）與圍壓的關系Fig.1 Relationship of confining pressure with compressive strength（a），young's modulus（b）and Poisson's ratio（c）

3 不同樣品脆性指數評價

3.1 基于傳統脆性指數模型的脆性指數評價

目前基于應力-應變特征計算巖石樣品脆性指數的方法主要有以下幾種（表3）。根據上述實驗測試結果，分別利用表3所列模型計算各個測試樣品的脆性指數，以便對各個模型的評價結果進行對比和分析。

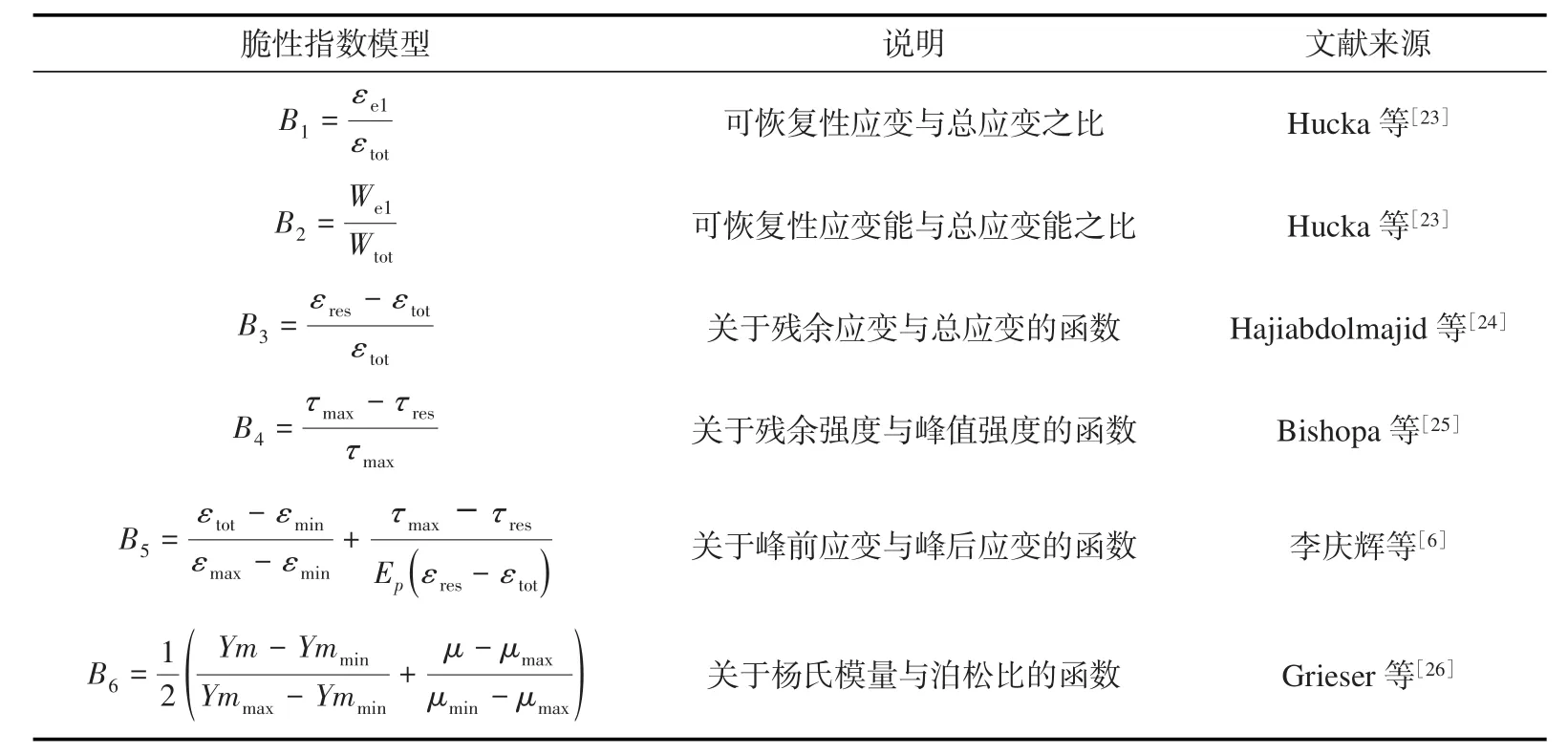
表3 幾種常見的基于應力-應變特征的巖石脆性指數模型Table 3 Several brittleness index model of rocks based on stress-strain characteristics

（1）應變和應變能

模型B1和B2分別用巖石可恢復應變占總應變的大小值、可恢復應變能占總應變能的大小值來評價巖石的脆性。分別計算了21塊測試樣品的可恢復性應變/總應變與可恢復性應變的關系（圖2）。從圖2可以看出，綠色框線內標出的部分樣品具有相近的可恢復性應變/軸向總應變值。5號泥巖樣品表現出典型的塑性破壞特征，13號砂巖樣品表現出典型的脆性破壞特征（圖3），且可見部分高脆性砂巖樣品的楊氏模量遠高于低脆性的泥巖樣品（參見表 2）。

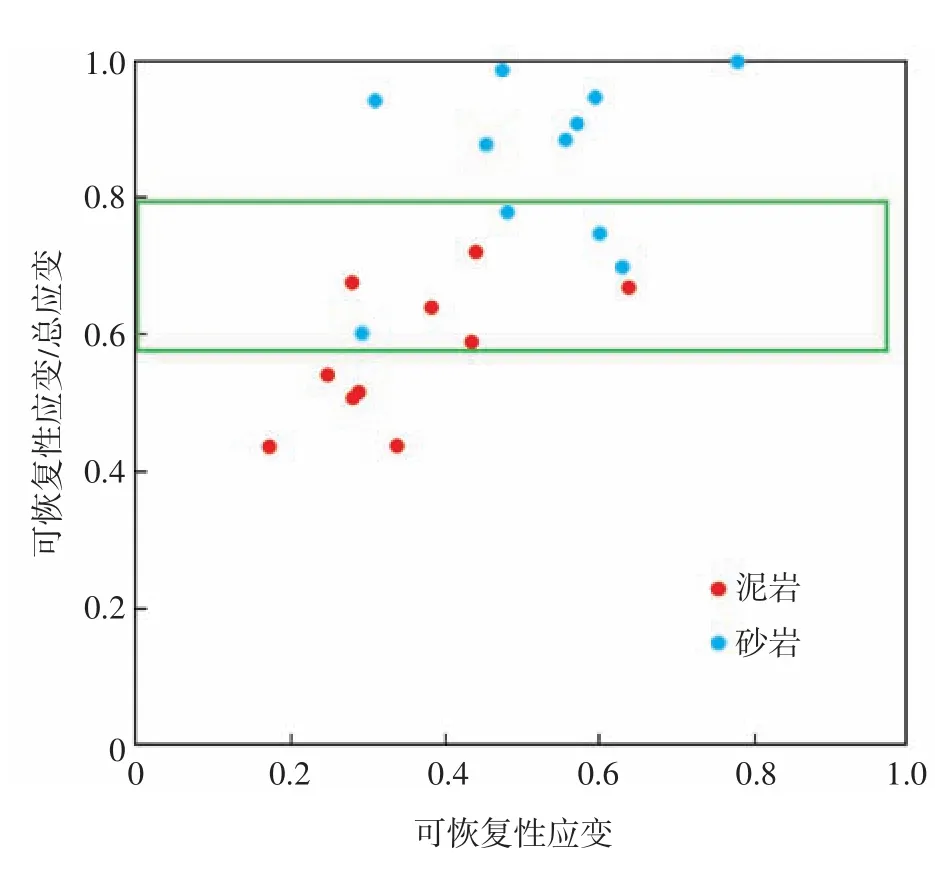
圖2 砂泥巖樣品的可恢復性應變/總應變與可恢復性應變的關系Fig.2 Relationship between the ratio of recoverable strain to total strain and recoverable strain of sand and mudstone samples

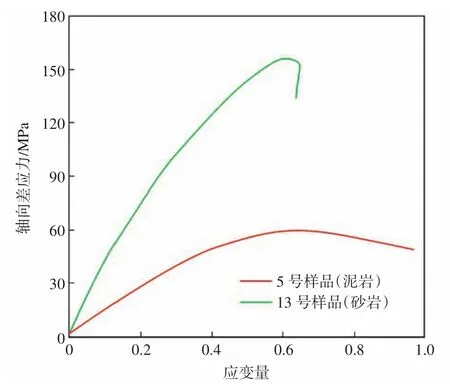
圖3 部分砂泥巖樣品的軸向差應力與應變量的關系Fig.3 Relationship between axial differential stress and strain of some sand and mudstone samples

（2）殘余強度

模型B3，B4，B5均考慮引入或者使用殘余強度評價泥巖的脆性，但是，由圖4可知，測試樣品1，2，4，8的峰后曲線并未呈現出塑性破壞特征，而是表現為典型的脆性破壞特征。分析原因認為，使用模型B3，B4，B5評價樣品的脆性時主要是基于試樣的破壞形式進行評價的，當樣品表現出應變軟化的變形特征，即峰后曲線斜率小于0，應變隨應力的增加而降低。對于部分泥巖樣品，其破壞形式為脆性斷裂，因此，這些評價方法不再適用。

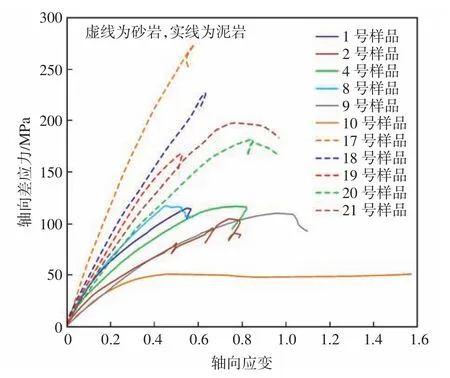
圖4 圍壓32 MPa下不同巖石樣品的應力-應變曲線Fig.4 Stress-strain curves of different rock samples under confining pressure of 32 MPa

（3）楊氏模量和泊松比

使用歸一化的楊氏模量和泊松比評價巖石的脆性是現場評價巖石脆性的重要方法。部分砂巖樣品與泥巖樣品具有相近的抗壓強度、楊氏模量和泊松比（圖5綠色圈中所示），其中10號樣品的塑性應變量遠高于21號樣品，21號樣品表現出典型的脆性破壞特征，10號樣品的塑性破壞特征較為明顯（圖6），可見僅使用楊氏模量和泊松比建立脆性指數，不能夠較好地適應巖石的脆性特征。

3.2 改進的脆性指數模型及評價

通過分析脆性指數與應力、應變參數的關系可知，抗壓強度、彈性模量及彈性應變與總應變之比越大、泊松比越小，則巖石的脆性越大。在具體區分巖石樣品脆性時傳統的脆性指數評價方法效果并不好，如泥巖可以有較高的楊氏模量，砂巖也可以有較低的楊氏模量和較高的泊松比。根據不同巖石樣品應力-應變曲線特征參數的差異，假設高脆性巖石具有高楊氏模量、低泊松比、高可恢復性應變量與總應變量之比、高屈服強度與抗壓強度之比的特征，建立這些參數與脆性指數的函數關系，并采用歸一化處理方法［式（1）—（4）］計算基于楊氏模量的脆性因子（BYm）、基于泊松比的脆性因子（Bμ）、基于可恢復應變與總應變的脆性因子（BRε）、基于屈服強度與抗壓強度的脆性因子（BRσ），建立綜合脆性指數Bn［式（5）］，進而對巖石樣品的脆性進行評價。

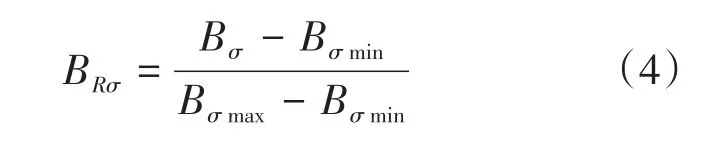
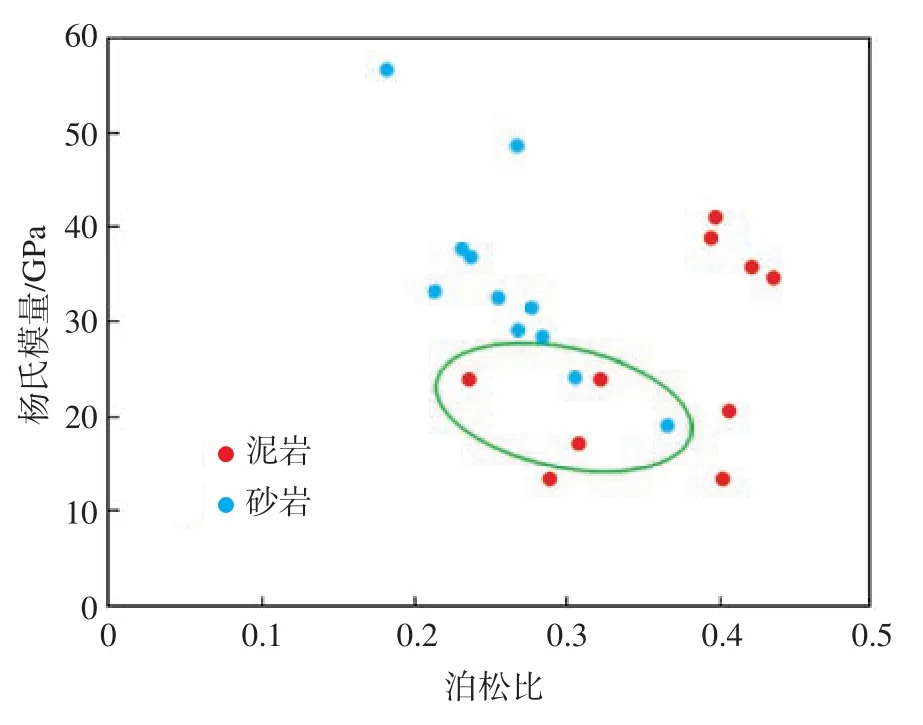
圖5 砂泥巖樣品楊氏模量與泊松比的關系Fig.5 Relationship between Young's modulus and poisson's ratio of sand and mudstone samples

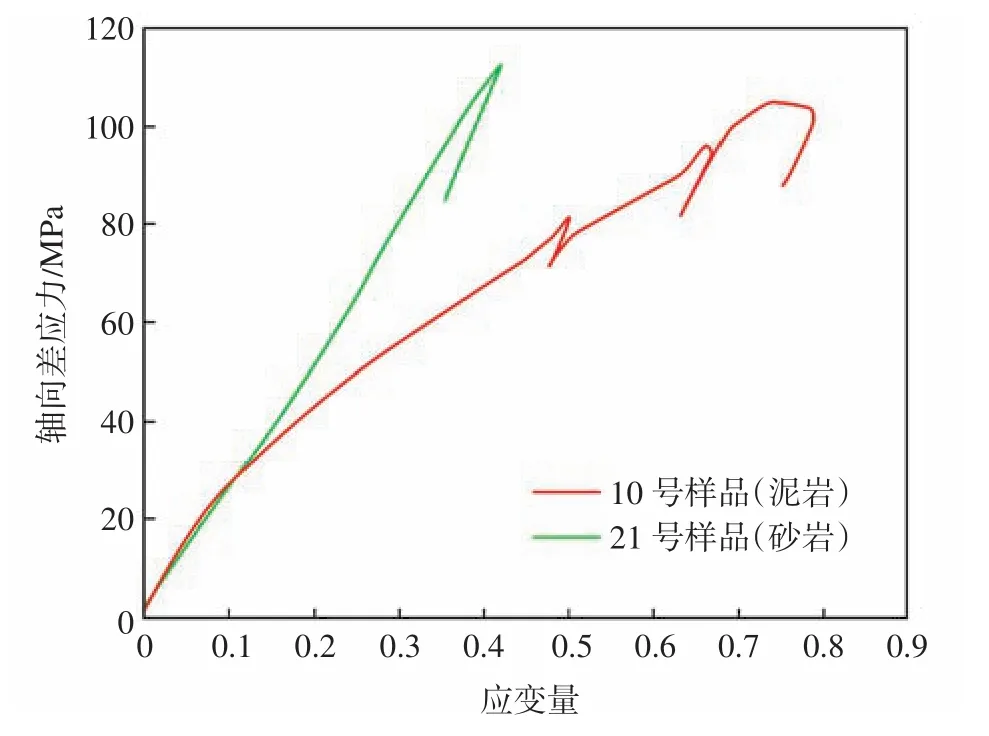
圖6 部分砂泥巖樣品的軸向差應力與應變量的關系Fig.6 Relationship between axial differential stress and strain of some sand and mudstone samples

綜合脆性指數由以上4個歸一化脆性因子聯合組成，即

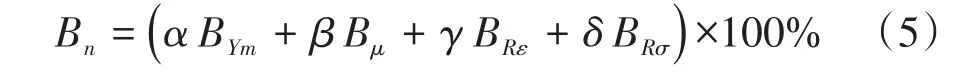
式中：α，β，γ，δ均為相關系數。

為了找出模型中可有效反映巖石脆性的脆性因子，開展如下工作：考慮到高脆性砂巖和低脆性泥巖的顯著差異，假設高脆性砂巖的脆性指數為1，低脆性泥巖的脆性指數為 0；對 Bn與 BRε，Bμ，BRσ，BYm的相關性分別進行了分析，結果表明Bn與BRε具有較好的相關性，而與 Bμ，BRσ，BYm也具有一定的相關性（表4）。多元回歸顯示，Bμ和BRσ沒有顯著差異（顯著性＞0.05）；共線性分析顯示，Bμ和 BRσ均存在嚴重的共線性（表5）。將共線性嚴重的影響因素排除，重新擬合。基于以上分析，認為在研究區脆性指數模型中Bμ，BRσ對于提高模型準確程度貢獻極小，可設β，δ取值為0，用BRε和BYm來表示巖石的脆性指數。通過多元回歸分析得到α，γ取值分別為0.477和0.662，即

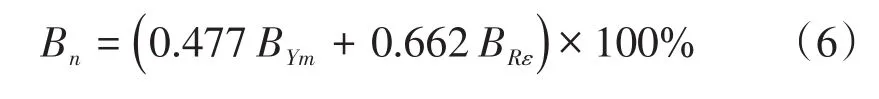
表 4 綜合脆性指數 Bn與 BYm，Bμ，BRε，BRσ 的相關性分析Table 4 Correlation analysis of comprehensive brittleness index（Bn）andBYm，Bμ，BRε，BRσ

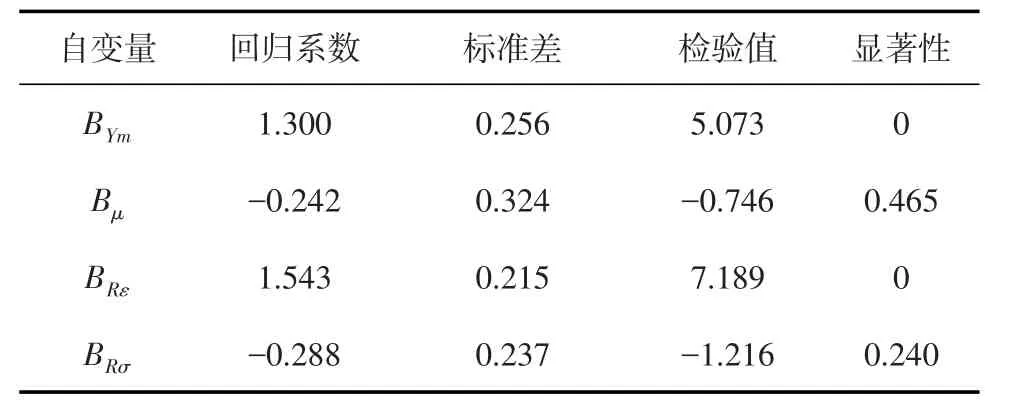
表5 回歸方程中自變量的顯著性分析Table 5 Significance analysis of independent variable in regression equation

通過分析可知，高脆性砂巖的脆性明顯高于低脆性泥巖的脆性，所以理想的脆性指數應該能夠明顯區分高脆性砂巖和低脆性泥巖。由圖7可知，B1和B6高脆性砂巖和低脆性泥巖脆性指數的分布區間存在重疊，不能明確對二者進行區分，而Bn高脆性砂巖和低脆性泥巖脆性指數的分布區間差異明顯，可見Bn在區分巖石脆性高低上較B1和B6具有更好的效果。

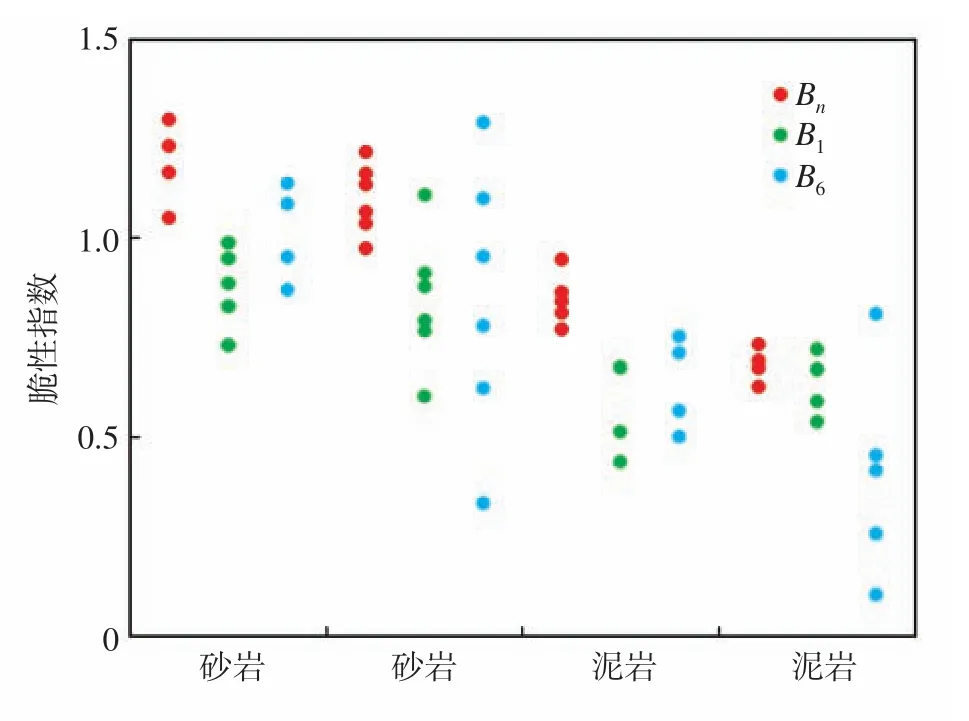
圖7 不同巖石樣品脆性指數評價Fig.7 Evaluation of brittleness index of different rock samples

4 結論

（1）選取四川盆地新場氣田須家河組五段的21塊砂泥巖樣品，基于不同樣品對應的應力-應變曲線特征參數的差異，對比分析了現有的基于應力-應變曲線的脆性評價方法，結果表明傳統的脆性指數評價方法在評價巖石脆性時效果不佳。

（2）分別計算了基于楊氏模量的脆性因子（BYm）、基于泊松比的脆性因子（Bμ）、基于可恢復應變與總應變的脆性因子（BRε）、基于屈服強度與抗壓強度的脆性因子（BRσ），綜合室內巖石力學測試結果建立了脆性指數 Bn與 BYm，Bμ，BRε，BRσ的函數關系式，并通過多元回歸方法建立新的脆性指數模型，評價結果表明該脆性指數模型能夠較好地區分研究區高脆性泥巖、低脆性泥巖和砂巖。