正用·逆用·靈活運(yùn)用

江蘇省海安市墩頭鎮(zhèn)仇湖初級(jí)中學(xué)八（2）班 孫 潤(rùn)

前些天寫作業(yè)的時(shí)候，遇到一道分式問題，它的解法太有意思了。

一開始拿到這道題的時(shí)候，我感覺無從下手，找不到解決問題的思路，但當(dāng)我再次看到題目中的“轉(zhuǎn)化成同分母的式子”的時(shí)候，再聯(lián)想到通分，就逐漸有了點(diǎn)頭緒。由于abc=1，于是我在第一個(gè)分式中嘗試湊abc，將分子、分母同時(shí)乘c，得到還真得到了一個(gè)和第3個(gè)分式同分母的分式。得出這個(gè)結(jié)論之后，我非常高興，接著嘗試將第2個(gè)分式的分母也化為ac+c+1，但將分子、分母同乘a之后，化成與第一個(gè)分式相同的分母，需再轉(zhuǎn)化一次，才能得到結(jié)果。

但第2天上課的時(shí)候，老師說，可以將第2個(gè)分式分母中的1換成abc，然后分子、分母約去b，就能達(dá)到化為同分母的目的。解答過程如下：

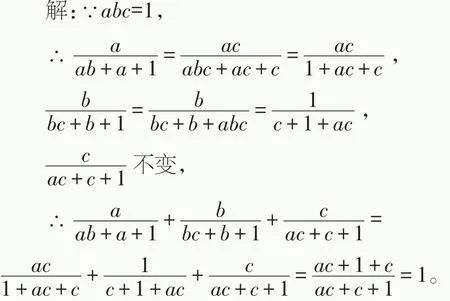
太巧妙了，利用abc=1這個(gè)條件，我們可以將題目中的abc換成1，也可以將1換成abc。

教師點(diǎn)評(píng)：小作者在解這道題目的過程中，體會(huì)到數(shù)學(xué)方法的巧妙，這是數(shù)學(xué)思維美的一種體現(xiàn)。我們平常做題目，總是喜歡將條件正用，但如果根據(jù)題目的特征，靈活運(yùn)用已知條件來解決問題，會(huì)收到意想不到的效果。