地鐵荷載下隧道周圍粉性土孔壓的單因素試驗

閆春嶺 張書石 李陽陽

（安陽工學院 土木與建筑工程學院 河南安陽 455000)

1 引言

動荷載作用下孔壓的變化規律是影響土體強度變化的重要因素之一，研究孔隙水壓力的發展規律，一是有助于了解土體在遭受外荷載作用下附加應力的分布狀況，二是進一步認識土體變形機制。因此，對循環荷載下土體的孔隙水壓變化規律的研究顯得尤為重要[1]。國內外一些專家學者對飽和土體在遭受動荷載作用時孔隙水壓力變化規律的認識有一定了解，如Seed等[2]對飽和砂土進行了一系列三軸試驗，得出了振動次數是影響孔隙水壓力的增長的一個不可忽視的因素，并提出了一種計算孔壓的理論表達式；Nasser等[3]對飽和的均勻松砂進行了大量的三軸試驗研究，首次從能量角度對孔壓增長規律進行了的解釋，隨后，Davis等[4]借助熱力學理論建立了土體能耗和孔壓增長之間的表達式；曹亞林等[5]對福建標準砂進行了大量三軸試驗，從土體累積耗損能量觀點，得出了孔隙水壓力增長的經驗表達式；謝定義等[6]對循環荷載下飽和砂土瞬時孔壓變化進行了相應的研究，對孔壓進行了相應的分類，并得到了孔壓的計算模型表達式。Chen[7]對未擾動的飽和軟黏土進行了大量的循環三軸試驗，研究了振動頻率對孔隙水壓力的變化規律，得到了對于給定的動態應力比，存在累積孔隙水壓力閾值，如低于此閾值，振動頻率對孔隙水壓力的影響非常小，反之，影響極大。Polito等[8]對砂土和粉性土進行了大量的循環三軸試驗，對孔隙水壓力采用了循環應力比及 Green-Mitchell-Polito兩種模型進行了研究。Lee等[9]對不飽和砂土進行孔隙水壓力三軸試驗研究，得出了隨著飽和度的降低，孔壓值顯著降低，在圍壓平均有效應力為30 kPa條件下，非線性變形特征略受B值影響。高軍[10]通過分析動三軸試驗結果，研究了孔隙水壓力與累積塑性應變之間的關系；肖東輝[11]、王世彪[12]、葛世平[13]、孟凡麗[14]通過土體的循環荷載試驗，研究了飽和土體的動孔壓模型。

目前，隨著城市化進程的推進，地鐵隧道設計埋深大多位于或穿越粉性土層。本文參考國內外專家學者的研究方法與成果，采用單因素試驗方法，結合方差分析，系統地研究動應力幅值、振動頻率及固結比對地鐵荷載下粉性土孔隙水壓力的影響程度和規律，該研究結果對地鐵隧道土體的長期沉降預測具有重要的理論價值和實際意義。

2 室內動三軸試驗

2.1 試驗儀器簡介

圖1 GDS動三軸循環系統

試驗采用英國進口多功能動態循環三軸系統GDS，如圖1所示。

2.2 試驗土樣

試驗土樣取自上海地鐵10號線國權路站附近②3層粉性土，其埋深為12.5m，該土層為Qh3的濱海-河口相沉積，厚約10m。粉性土的基本物理力學參數見表1。

表1 土體的基本物理力學指標

2.3 試驗準備工作

首先切取土樣，試樣加工制成高為10 cm，直徑為5 cm的圓柱土體；其次為了使試樣表面水力貫通，便于滲透，黏貼濾紙條，寬度約1 cm，并均勻布置在試樣兩側（3～4條），同時在兩端頂部分別貼上圓形濾紙；再次小心謹慎套乳膠膜，保證不擾動試驗為準；最后，往壓力倉注純凈水，開始試驗。

3 單因素試驗設計及結果

在本次試驗中，考慮地鐵影響土體孔隙水壓力的因素為振動頻率、動應力幅值及固結比。根據文獻[15]，本次試驗采用的頻率為0.5 Hz，1.5 Hz，2.5 Hz；根據文獻[16]，動應力幅值取20 kPa，30 kPa，40 kPa；根據土樣本身的物理力學指標及工程實際經驗，將試驗中固結比取1，2.5，3.3[17]。最終試驗結果列于表2。

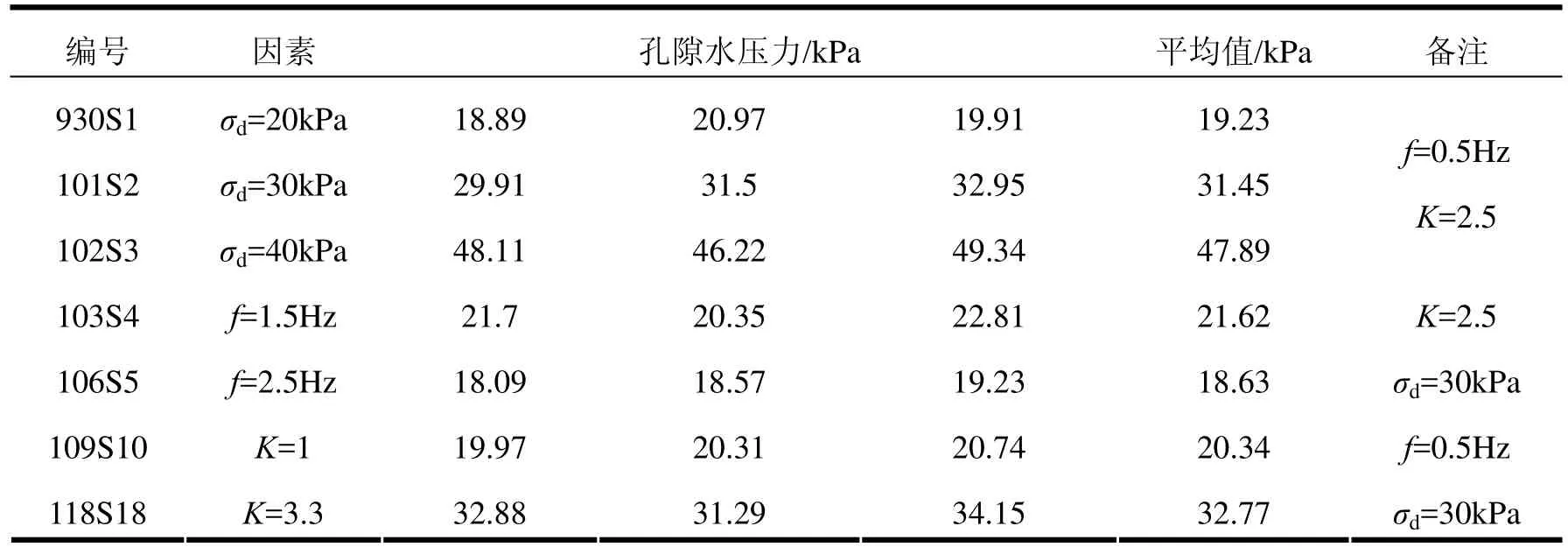
表2 地鐵荷載下粉性土的孔隙水壓力

4 試驗結果的方差分析

設某單因素A有r個水平A1，A2，…，Ar，在每個水平下分別做了ni（i=1，2，…，r)次試驗，按數理統計的方法，單因素方差分析步驟如下：

4.1 計算平均值

所以組內和為：

4.2 計算離差平方和

（1）總離差平方和

ST表示各試驗值與總平均值的偏差的平方和。

（2）組間離差平方和

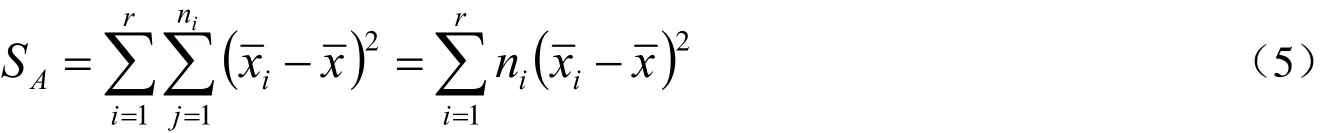
SA表示因素A組間離差平方和。

（3）組內離差平方和

Se表示組內離差平方和。

4.3 計算自由度

（1）總自由度

（2）組間自由度

（3）組內自由度

式中，dfT為總自由度；dfA為組間自由度；dfe為組內自由度。

4.4 F檢驗

將各因素的平均離差的平方和與誤差的平均離差的平方和分別相比，得到F值

FA為因素A的F值。如果，則認為因素A對試驗結果有顯著影響，否則認為因素A對試驗結果沒有顯著影響。

4.5 各因素對孔隙水壓力的方差分析

按上述步驟，對表2的數據進行計算，考慮工程中的實用性，給出檢驗水平α=0.05及α=0.01，從F分布表中查得F0.05（2，6）=5.14，F0.01（2，6）=10.93。結果列于表3～表5。從表3～表5中可看出，振動頻率、動應力幅值及固結比對孔隙水壓力均有非常顯著的影響。

表3 振動頻率對孔隙水壓力的方差分析

表4 動應力幅值對孔隙水壓力的方差分析

表5 固結比對孔隙水壓力的方差分析

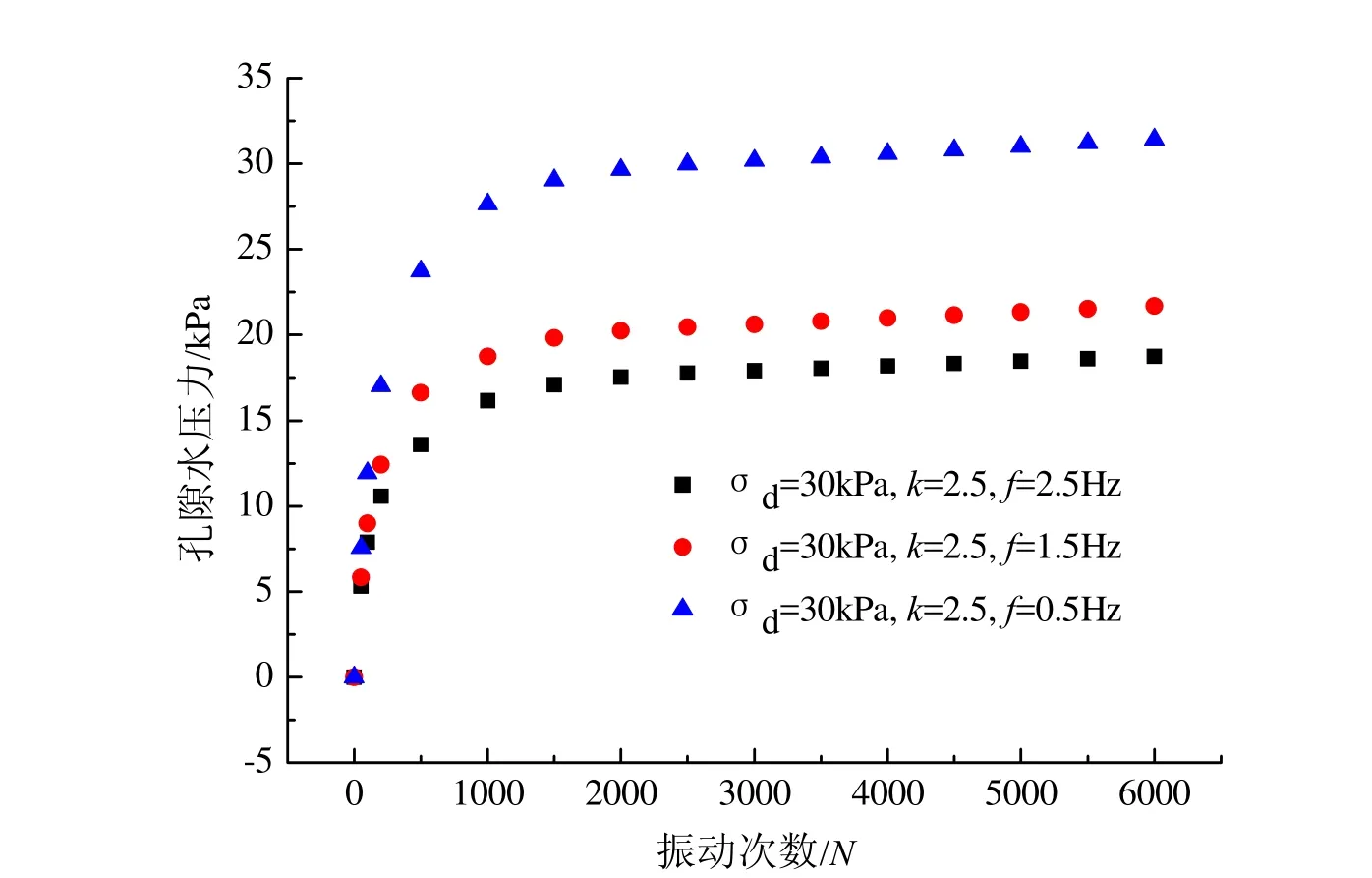
圖2 不同頻率的孔隙水壓力與振動次數關系

4.6 各因素對孔隙水壓力的分析

圖2為動應力幅值為30 kPa，固結比K=2.5，不同頻率的孔隙水壓力與振動次數關系曲線，從圖4可以看出，隨著振動次數的增加，粉性土的孔隙水壓力逐漸增大。在相同振動次數下，低頻（0.5 Hz）產生孔隙水壓力較大，高頻（2.5 Hz）產生的孔隙水壓力較小。

圖3 不同荷載幅值的孔隙水壓力與振動次數關系

圖3為固結比為2.5，頻率為0.5 Hz，不同荷載幅值的孔隙水壓力與振動次數關系曲線，由圖5可知，當荷載幅值較小時，隨著振動次數的增加，孔壓逐漸上升，但上升的速率較小；當作用較大的荷載幅值時，土體將在較短的時間內產生較大的孔壓。

圖4為動應力幅值為30 kPa，振動頻率為0.5 Hz，不同固結比的孔壓隨振動次數的關系曲線，本文采用的固結比分別為1，2.5及3.3，軸壓一定，固結比越大，產生的孔壓就越大。

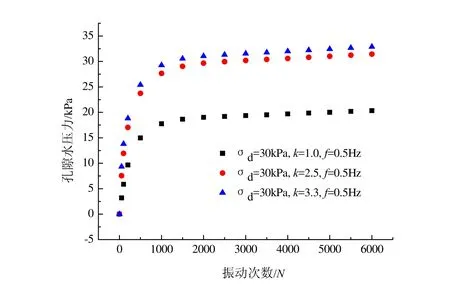
圖4 不同固結比的孔壓隨振動次數的關系

5 結論

通過對上海地鐵10號線附近的粉性土進行多功能GDS循環三軸試驗，考慮了振動頻率、動應力幅值及固結比等因素對孔隙水的影響，得到：

（1）相同振動頻率及固結比條件下，動應力幅值越大，產生的孔隙水壓力就越大；相同動應力幅值及固結比條件下，頻率越小，產生的孔隙水壓力就越大；相同動應力幅值及振動頻率下，固結比越大，產生的孔隙水壓力越大。

（2）從孔隙水壓力與振動次數的關系中可以看出，孔隙水壓力經過快速增長-緩慢增長-衰減穩定三個階段的變化過程，因此，地鐵運營初期是防止孔壓增長控制的重點。

（3）通過單因素及方差分析方法，得到振動頻率、動應力幅值及固結比均對孔壓有非常顯著的影響。