中考中的一元一次不等式問題

◎肖學軍

一元一次不等式是初中數學的基礎性內容，時常成為中考命題中必不可少的測試內容。本文擬以2018年部分省市的中考題為例，按考點歸類加以剖析。

考點一：不等式的性質

例1（2018·宿遷）若a＜b，則下列結論不一定成立的是（ ）。

【解析】由不等式性質容易知道，選項A、B、C中的不等式是成立的。選項D有時成立，如當a、b均為正數時成立；有時又不成立，如當a=-2，b=1時。故答案選D。

【點評】本題主要考查不等式的性質，我們只要掌握了不等式的性質便容易作出正確判斷。本題要尋找的是不一定成立的結論，不是錯誤結論，這是審題時必須要引起重視的。

考點二：求不等式（組）的解集及其數軸表示

例2（2018·威海）解不等式組并將解集在數軸上表示出來。

【解析】解不等式①，得x＞-4；解不等式②，得x≤2。根據“大小小大中間找”，可得原不等式組的解集為-4＜x≤2，在數軸上表示如下圖所示：

【拓展】（2018·貴港）若關于x的不等式組無解，則a的取值范圍是（ ）。

A.a≤-3 B.a＜-3 C.a＞3 D.a≥3

解決本題的關鍵是要利用不等式組取解集的方法，將問題轉化為不等式：a-4≥3a+2，答案為A。

【點評】這類問題是不等式問題的常見題型。要能夠熟練應用求不等式組解集的法則，即“同大取大，同小取小；大小小大中間找，大大小小無解了”。

考點三：不等式（組）的整數解問題

例 3（2018·包頭）不 等 式組的非負整數解有________個。

【解析】首先解不等式組，得到不等式組的解集為x＜4，從而該不等式組的非負整數解為0、1、2、3這4個，故答案為4。

【拓展】（2018·荊門）已知關于x的不等式3xm+1＞0的最小整數解為2，則實數m的取值范圍是（ ）。

A.4≤m＜7 B.4＜m＜7

【點評】這兩題均為不等式的整數解問題，例3比較直接，通過解集得出答案；拓展題關鍵是要由最小整數解得出符合題意的不等式。

考點四：不等式（組）的應用問題

例4（2018·南京）如圖，在數軸上，點A、B分別表示數1、-2x+3。

（1）求x的取值范圍；

（2）數軸上表示數-x+2的點應落在___。

A.點A的左邊 B.線段AB上

C.點B的右邊

【解析】（1）根據數軸上的點表示的數右邊的總比左邊的大，可得不等式-2x+3＞1，解得答案x＜1；

（2）由x＜1，得-x＞-1，于是有-x+2＞-1+2，根據不等式的性質，可得點在A點的右邊；根據作差法：-2x+3-（-x+2）=1-x＞0，可得點在B點的左邊。故選擇B。

【拓展】思考1.若將（2）中的點記為C點，這三點中存在某點是另外兩點所構成線段的中點嗎？

由（2）解答知C點在線段AB上，故只有C點有可能為線段AB的中點。計算AC和BC長度可知，結論成立。

思考2.若點B右側有一點D所表示的數是2x+5，且2＜BD≤6，試求x的取值范圍。

事實上，BD=（2x+5）-（-2x+3）=4x+2。根據題意可得不等式組解得0＜x≤1。又由問題（1）知x＜1，所以x的取值范圍為0＜x＜1。

【點評】本題主要考查同學們靈活應用不等式的有關知識解決問題的能力，既考查了應用數軸比較兩個實數大小和不等式的性質應用，又著重考查了數形結合的思想。

例5（2018·濟寧）“綠水青山就是金山銀山”，為保護生態環境，A、B兩村準備各自清理所屬區域養魚網箱和捕魚網箱，每村參加清理人數及總開支如下表：________________________________

10__________________________________16 68000_________村莊清理養魚網箱人數/人_____清理捕魚網箱人數/人_____總支出/元________A______B__15 9__________57000

（1）若兩村清理同類漁具的人均支出費用一樣，求清理養魚網箱和捕魚網箱的人均支出費用各是多少元；

（2）在人均支出費用不變的情況下，為節約開支，兩村準備抽調40人共同清理養魚網箱和捕魚網箱，要使總支出不超過102000元，且清理養魚網箱人數小于清理捕魚網箱人數，則有哪幾種分配清理人員方案？

【解析】（1）設清理養魚網箱的人均費用為x元，清理捕魚網箱的人均費用為y元，

（2）設m人清理養魚網箱，則（40-m）人清理捕魚網箱，根據題意，列不等式組

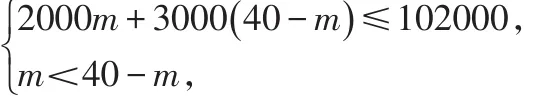
解得：18≤m＜20，

∵m為整數，∴m=18或m=19。

則分配清理人員方案有兩種，

方案一：18人清理養魚網箱，22人清理捕魚網箱；

方案二：19人清理養魚網箱，21人清理捕魚網箱。

【拓展】思考1.這些方案中，哪種方案總支出較少？

對此，可以分別求出兩個方案的總支出，通過比較可知方案二總支出較少。

思考2.若將總支出改為不超過110000元，問有幾種分配方案？其中哪種方案總支出最少？

仿照本題解法可得10≤m＜20，用列表法知共有10種方案。若分別求出10種方案的總支出，則很繁雜。由于總支出代數式為2000m+3000（40-m），化簡即為120000-1000m，易知m越大，總支出越少。10種方案中，還是m=19時的方案總支出最少。

【點評】本題主要考查同學們運用二元一次方程組和不等式組的有關知識來解決實際問題的能力。題目中的有關信息由表格給出，問題（1）較為容易，所涉及的兩個未知量通過列出二元一次方程組即可求解；問題（2）中有兩個不等關系，這是列出不等式組的重要依據。