春運期間中國航空網絡拓撲結構實證分析*

楊 泳 徐開俊 李珊珊 吳佳益

(中國民用航空飛行學院 廣漢 618307)

0 引 言

航空網絡中節點間的航線連接顯然既不屬于完全規則連接，也不是完全隨機連接，屬于復雜網絡的典型實際應用.復雜網絡已經成為研究具有復雜特性的航空網絡的最有效工具，在航空網絡的負載特性、級聯失效特性、路徑優化及抗毀性特性等方面得到廣泛研究和運用[1-2].

目前，借助復雜網絡理論提供的統計特征指標，如度分布、平均最短路徑、介數、最大連通子圖、聚類系數等，對世界航空網絡、北美航空網絡和中國航空網絡均進行了理論及實證研究，并取得了有影響力的工作.Guimera等[3]從復雜網絡的拓撲結構研究出發，證實世界航空網絡和北美航空網絡是小世界網絡，存在冪律下降的度分布和介數分布，且發現最中心的機場不一定是介數最大的節點；曾小舟等[4-5]對國內航空網絡進行了實證分析，中國國內航空網絡是服從雙段冪率度分布的小世界網絡，且網絡出現以度值較大的機場為中心的群體結構； Zhang等[6-7]均針對國內航路網絡與航線網絡進行了實證對比分析，Bagler等[8-9]對印度航空網絡進行了實證分析.

雖然這些理論和實證研究做出了許多有影響力的工作，但鮮有針對中國春運期間的航空網絡進行實證研究，針對相關性方面的實證研究目的和結論也相差較大.本文針對春運期間中國航空網絡的拓撲特性、度-度相關性、度-介相關性、度-聚相關性等問題進行研究，其結果可為后續進一步對中國航空網絡的網絡結構優化和規劃建設提出科學性的合理建議.

1 復雜網絡結構特征量

1.1 度和度分布

度在不同的復雜網絡中所代表的具體含義不同，對于航空網絡而言，節點機場度值大小直接表示機場通航航線的多少.一般情況下，某個機場的度值越大，則該機場在整個航空網絡系統組織中的作用和影響也越大，反之亦然.網絡中度的表示一般用平均度、度分布p(k)和累積度分布P(k)表示，定義為

(1)

p(k)=N(k)/N

(2)

(3)

式中：ki為機場i的度；N為網絡機場數；N(k)為網絡中度值為k的機場數.網絡的平均度反映了整個網絡的稠密程度，本文中的FCAN網絡的平均度為21.93，即春運期間平均每個機場約與其它22個機場有直達航線.

1.2 聚類系數

聚類系數也是網絡結構的一個重要屬性，節點聚類系數表征該節點的鄰居節點之間連通的概率，而網絡平均聚類系數刻畫了網絡中機場成簇的內在傾向性，是網絡中機場群集性的特征描述.本文中FCAN網絡為0.68，表現出較強的聚集性，同時進一步計算其具有較小的平均最短路徑長度為2.12，因此，可以認為該網絡是小世界網絡.

機場節點的聚類系數可以定義為

(4)

(5)

式中：ki為機場i的度；ei為機場i的鄰居機場直接連接航線的條數.

1.3 介數

介數在航空網絡中能夠反映機場或某條航線在網絡中的影響力，可以分為機場節點介數和網絡航線邊介數.機場節點i的介數可以定義為

(6)

式中：nab為從機場a到機場b之間的最短路徑的數量；nab(i)為從機場a到機場b的所有最短路徑中經過機場i的航線數.

1.4 度-度相關性

度-度相關性指標描述的是節點之間根據度值作為相互之間連接的選擇偏好性，通常通過比較度為k的近鄰節點度和計算網絡的同配性系數進行分析.機場i所有鄰近節點j的近鄰平均度定義為

(7)

將網絡中度為k的所有節點N(k)的鄰節點的knn,i進行平均得到“度為k的節點近鄰平均度”，為

(8)

式中：ki為機場i的度；V(i)為機場i的鄰近機場集合；ki為機場i的度；N為網絡機場數；N(k)為網絡中度值為k的機場數.

網絡同配系數能夠刻畫網絡中所有機場度傾向性的互連模式，是廣泛使用的節點度相關性指標，可以定量刻畫網絡的同配混合性，它定義為

(9)

式中：M為網絡中機場總邊數；ji和ki分別為第i條航線連接的兩個機場的度.從同配系數的定義滿足-1≤r≤1：當r<0時，度大的機場傾向于和度小的機場建立航線，此時的網絡是度-度負相關的，即航空網絡是異配網絡；而當r=0時，網絡為中性網絡；當r>0時，網絡中度大的機場傾向于與度大的機場相連，度小的機場傾向于和度小的機場相連，此時的網絡稱為同配網絡，或者說網絡是度-度正相關的.本文中FCAN網絡r為-0.43，表明網絡整體呈現度-度負相關性.

2 網絡構建及分析

2.1 數據來源及網絡構建

復雜網絡是由許多表示個體的節點和表示個體之間關系的連接邊組成，航線網絡的節點由機場組成，而邊由直飛的航線組成.本文研究最新基礎統計數據來源于民航數據通訊公司，統計了2018年1月22日—2月22日之間所有國內民用航空航空公司實際執飛的所有起點和終點均位于國內的直飛航線數據.

整個春運期間中國國內航空網絡(festival chinese airline networkx, FCAN) 包含226個機場構成的節點，2 479條實際航線構成的邊，而所有相關機場節點的經緯度是借助電子飛行包(EFB)查詢各個機場ARP點獲得.數據經過收集、統計、分析、整理后，利用Python編程，輔助Networkx復雜網絡建模工具、Matplotlib繪圖庫、Numpy科學計算包等工具構建中國航空網絡，網絡結構圖見圖1.

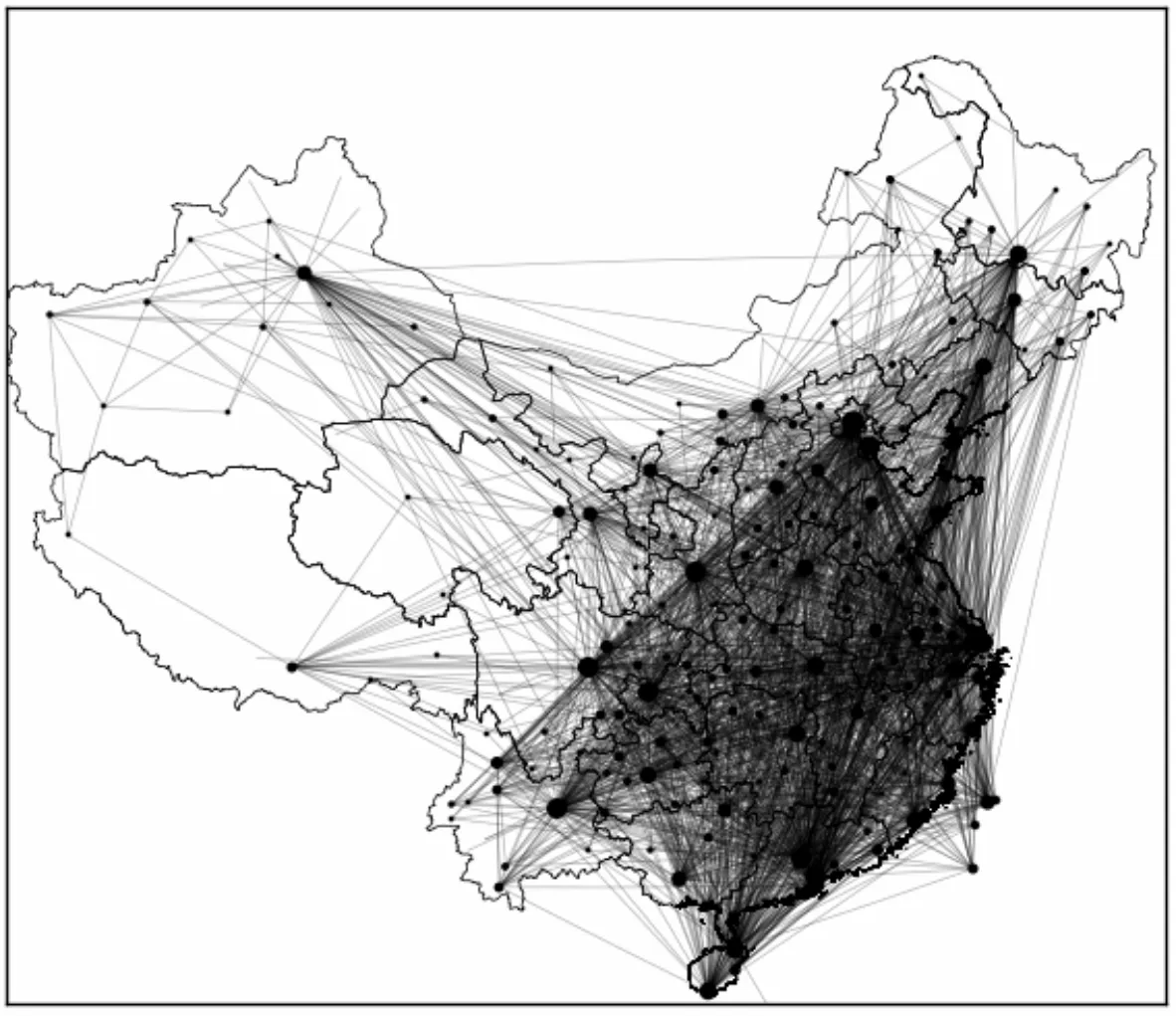
圖1 CAN網絡結構圖

2.2 拓撲特性分析

利用Python編程計算FCAN網絡的度分布及機場節點的度分布、累積度分布及重要指標的散點圖，見圖23.

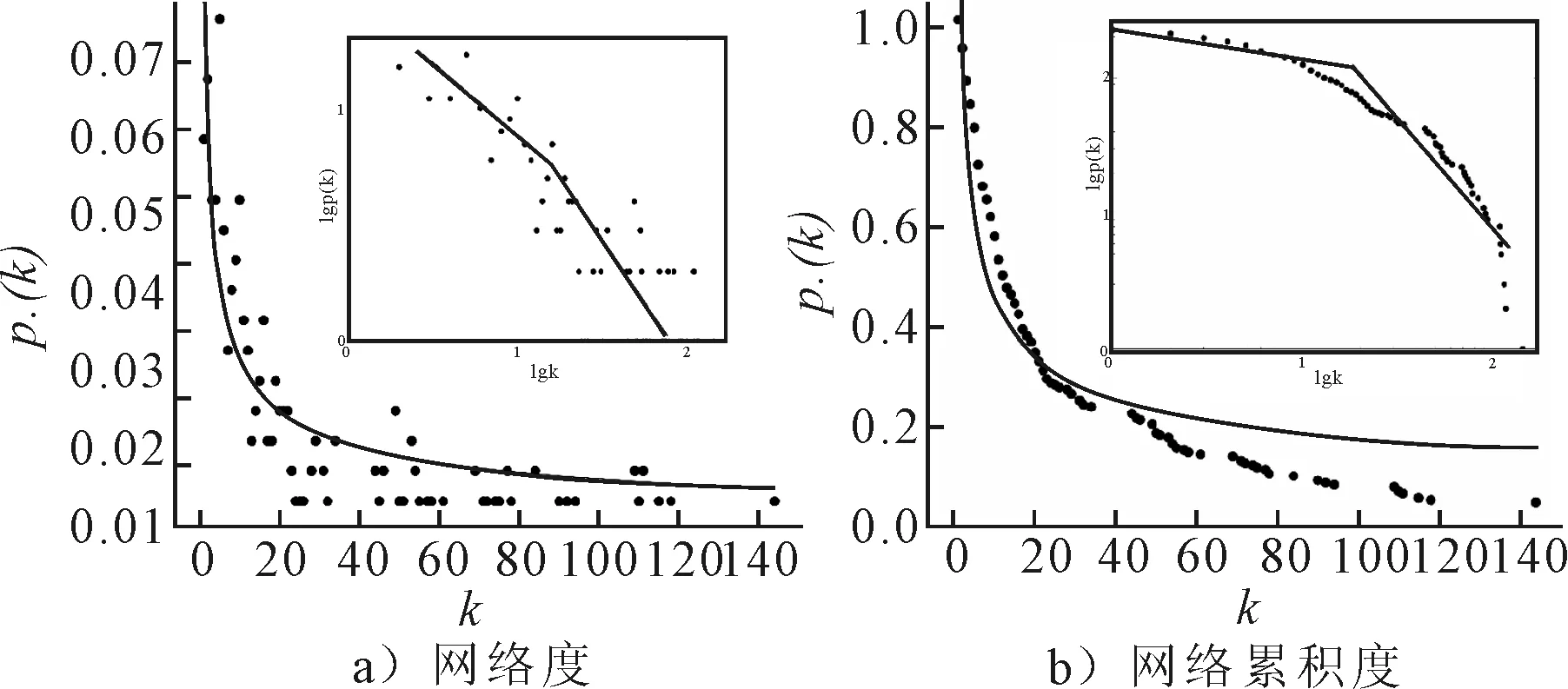
圖2 FCAN分布圖

圖3 機場度值和介數統計

圖2為FCAN的度分布及累積度分布，橫坐標k為度值，縱坐標p(k)為該度值對應的機場數占整個FCAN網絡中機場總數的概率.由圖2可知，FCAN網絡的度/累積度分布均符合冪律分布規律的，說明網絡具有典型的無標度特征.進一步觀察FCAN網絡的度/累積度分布圖，反映出FCAN節點服從雙段冪率分布，絕大部分機場度值小于22，而度值大于22的機場僅占機場總數的20%，且分布在度值22145的廣大范圍內.

圖3為顯示FCAN網絡中各機場節點度和介數的值分布情況，由圖3可知，FCAN網絡中有相當大部分機場的度和介數為0的孤立支線機場，而度值較大或運輸能力強的航線占比較少，說明我國航空運輸潛力還有待進一步挖掘.

2.3 相關性分析

圖4為FCAN網絡所有機場介數-度值分布關系，由圖4a)可知，介-度呈現較明顯的指數相關性，但烏魯木齊機場ZWWW哈爾濱太平機場ZYHB介數明顯較大，因為ZWWW機場是西北航空樞紐和中轉中心，而哈爾濱作為東北的重要航空樞紐和中轉中心，近年來經濟發展和航空運輸均呈現迅猛發展；由圖4b)可知，介-度在總體正相關趨勢下，在度值較小時呈現出較大的“波動性”，這與文獻[7]世界網絡表現出相似的特性.

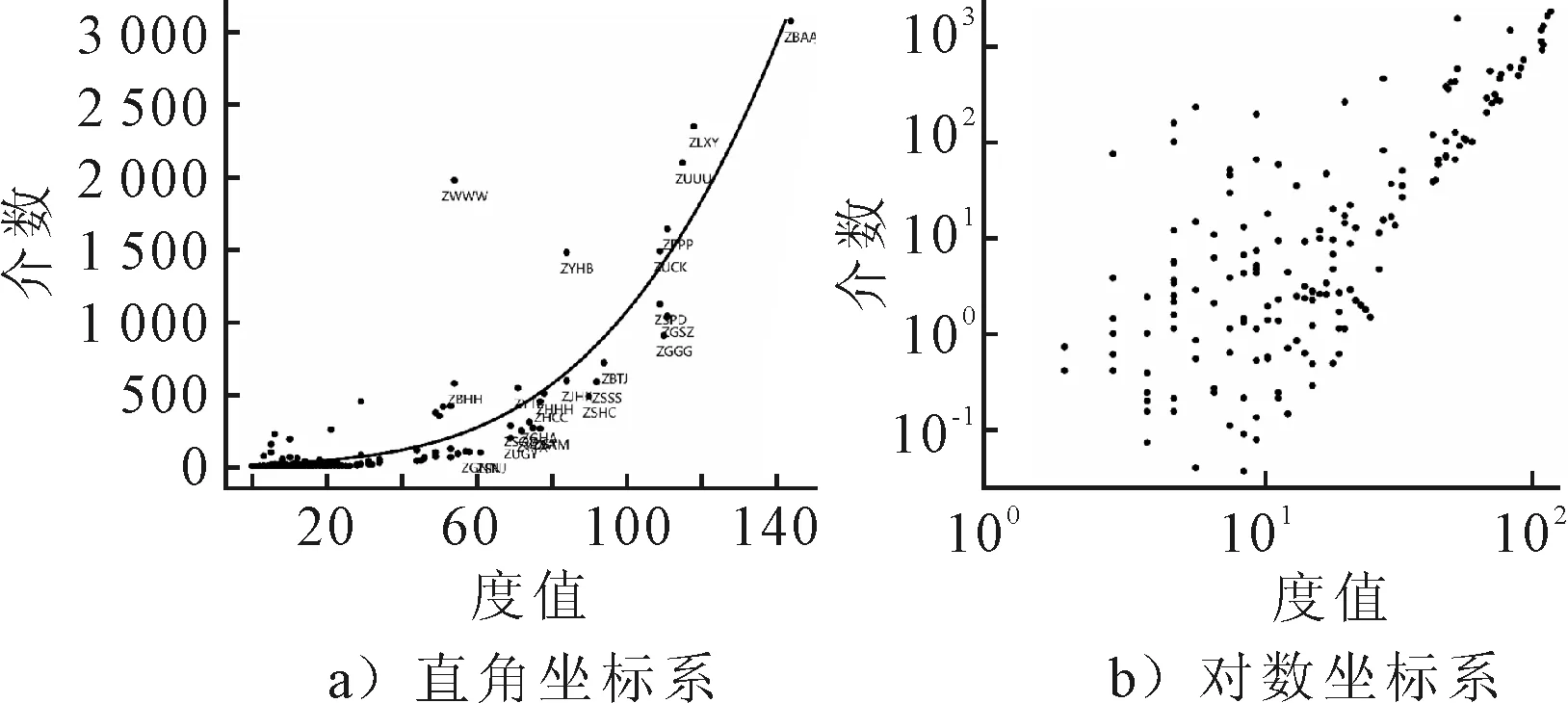
圖4 機場介數-度相關性分布圖

圖5為FCAN網絡的聚類系數-度相關性.由圖5a)可知，聚類系數與度的關系可以近似表示為c(k)～k-α，說明網絡具有明顯的層次性，即航空網絡可以按照某種規則劃分為明顯的層；由圖5b)可知，在大部分區域(k>10)內，FCAN具有明顯的聚-度負相關性，說明度小的城市比度大的城市更傾向于集聚成團，而(k<10)時由于大部分孤立機場的存在使得聚類系數保持在常量1.0附近.

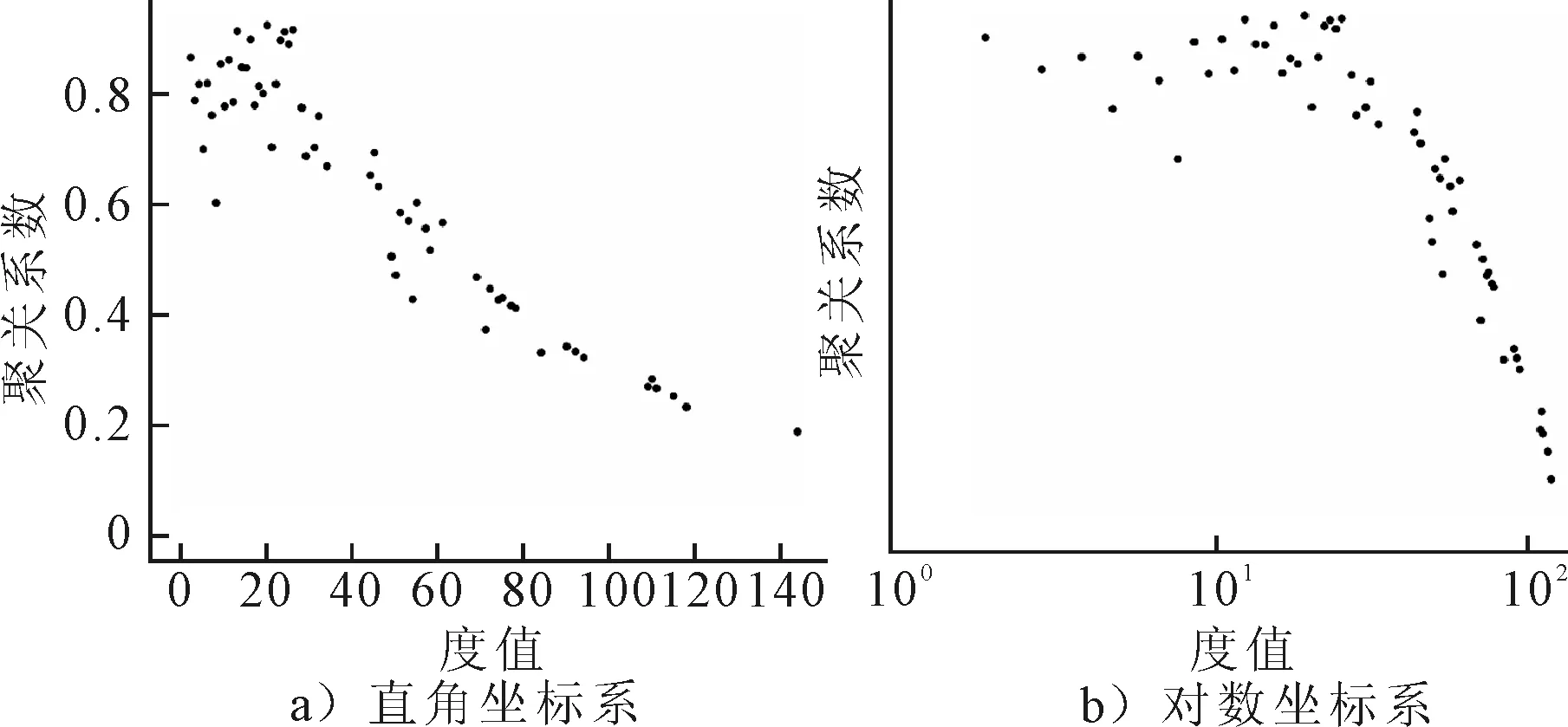
圖5 機場聚類系數-度相關性分布圖

圖6為FCAN網絡的近鄰節點平均度knn(k)-度相關性.

由圖6可知，當k>10時呈現明顯的負相關性，說明度大的節點傾向于連接度小的節點；但當度值較小k<10時，knn(k)并無明顯規律，幾乎是常量，這與文獻[3]對北美航空網絡的研究結果相似，區別在于Barrat的研究結論顯示趨勢拐點在于度值k=30附近，筆者認為這主要是由于航線網絡的規模和連通性共同決定.能否進一步將這種拐點的度值用于表征不同經濟發展水平國家的航運能力及網絡規模，還需要進行大量的實證資料和更深入的研究.

3 結 束 語

FCAN網絡是具有較短的平均路徑長度和較大的聚類系數的小世界網絡，即節點度/累積度分布均滿足雙段冪律分布規律的，度值大于28的機場僅占機場總數的20%左右，具有典型的無標度特征.介-度總體呈現較明顯的指數相關性，在度值較小時呈現出較大的“波動性”；聚-度相關性表明網絡具有明著的層次性且在大部分區域(k>10)內網絡呈現明顯的聚-度負相關性，即表明度小的城市比度大的城市更傾向于集聚成團；近鄰節點平均度kn,n-度相關性表明，當k>10時呈現明顯的負相關性，但度值較小(k<10)時，kn,n幾乎是常量.