關于智能算法在土木工程中的應用

(華南理工大學土木與交通學院 廣東 廣州 510641)

一、灰色系統理論的概述

灰色系統理論(Grey System Theory)是由我國華中理工大學鄧聚龍教授首創的一種新的系統理論，結合運用數學方法而形成的一套解決信息不完備系統即灰色系統的理論和方法。[1-2]

二、灰色系統理論的研究內容

基于灰色建模理論的灰色預測法，按照其預測問題的特征，可分為五種基本類型，分別是：

(1)數列預測

(2)災變預測

(3)季節災變

(4)拓撲預測

(5)系統預測

灰控制目前主要是指灰色預測控制，這是單序列建模的控制。[2]

三、灰色系統理論的設計思路

定義1 設初始序列為{x(0)(k)}={x(0)(1),x(0)(2),…,x(0)(n)}[3]

其中k表示數據序列時刻，初始數據是0次累加數據，原始數據一次累加序列定義為：

n次累加序列定義為：

定義2經過r次累加數據序列x(r)(k)的0次數據累減為：

α(0)(x(r)(k))=x(r)(k)

一次數據累減定義為：

α(1)(x(r)(k))=x(r)(k)-x(r)(k-1)=x(r-1)(k)

n次數據累減定義為

α(n)(x(r)(k))=α(n-1)(x(r)(k))-α(n-1)(x(r)(k-1))r=1,2…

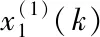
該方程叫GM(n,h)模型，當n=1且h=1時，GM(n,h)模型退化為GM(1,1)模型，它是灰色系統理論中使用最廣的模型，是一種單序列的一階線性動態模型，其微分方程為：

令：

從而有：

yn=aX+uE

用最小二乘法求得方程的待定系數a，u。

由一階線性微分方程的通解離散化可得GM(1,1)模型的響應函數(時間序列)為：

系統還原值為：

初始條件：

故：

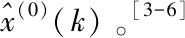
四、灰色理論在土木工程中的應用

灰色系統理論可使一些隨機上下波動時間序列的離散數據通過累加生成或積分生成的方式均可變為非負的、單調增加的、帶有線性或指數律的序列。因此，用灰色系統理論作指導，建立灰色GM(1,1)模型，用以預測混凝土材料塌落度、抗拉強度、抗壓強度等等，是可行的。

案例1預測混凝土抗壓強度

此實驗數據為再生混凝土取代之后，研究其在固定配合比下，混凝土的28d抗壓強度。當再生粗骨料的取代率為30%時，研究水灰比對其強度的影響。通過GM(1,1)數據建模，可預測不同水灰比下再生混凝土的強度值。

在Matlab程序GM(1,1)中輸入數據，將水灰比作為等差默認序列，將實際28d抗壓強度數據作為已知數據，鍵入

[x,y,z]=gm11done([35.8,28.2,26,25.5,22.3,21.1],7)，

其中“x”表示預測的數組，“y”表示平均相對誤差(百分比)，“z”表示關聯系數，“7”表示要預測的個數。則運行程序之后，可以得到：