改進的卡爾曼濾波在MEMS陀螺儀信號處理的應用

張伯源 高國偉

北京信息科技大學傳感器重點實驗室，北京 100101

一、引言

隨著MEMS技術的快速發展，微機械（MEMS）陀螺儀在體積、重量、成本上優勢十分明顯[1-5]，目前已廣泛應用于無人機、吊艙、戰術導彈、慣性導航等各個領域。角速率的測量是慣性導航領域里的關鍵參數之一，但其精度問題限制了其在慣性導航領域的進一步發展。對MEMS陀螺儀信號誤差進行辨識分析、建模補償是提高陀螺儀角速率測量精度的重要方法[6]。

MEMS陀螺誤差包括固定常值漂移（零偏）、標度因數誤差、非正交安裝誤差、溫度漂移誤差以及隨機漂移誤差[7]，其中固定常值漂移（零偏）、標度因數誤差、非正交安裝誤差、溫度漂移誤差能夠使用高精度三軸轉臺設備校準以減小對測量結果的影響[8]。而隨機漂移誤差是陀螺儀在外界各種干擾力矩的作用下偏離原來的方向產生的，它隨時間、外界環境條件不斷變化，難以使用標定方法進行處理。

首先，本文介紹了隨機誤差辨識的Allan方差法，并對MEMS陀螺隨機誤差進行了時間序列分析，建立基于時間序列的陀螺儀誤差模型，接著在經典卡爾曼濾波器的基礎上加入衰減因子和一階低通濾波后的差分控制項進行自適應估計補償，最后結合硬件系統進行試驗，并利用Allan方差法對濾波前后的效果進行對比分析。

二、模型分析與濾波算法原理

1、Allan方差法

Allan方差法的提出主要用于分析振蕩器的頻率和相位的不穩定性，也常用于定量地對陀螺儀各項隨機誤差進行辨識[9]，誤差分離結果較好，可以作為通過不同算法對陀螺儀補償前后評價其性能的重要指標。

假設陀螺儀的樣本信號長度N，采樣頻率f，則采樣間隔為1/f。然后把樣本數據平均分成K個子序列，每個子序列有n=N/K個樣本，每個子序列的時間長度稱為相關時間t=nf(n＜N/2)，則每個序列的平均值)為：

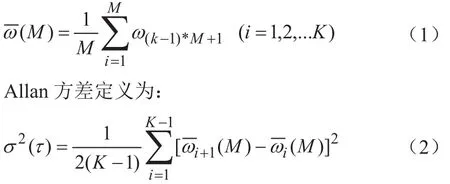
以Allen方差法分析MEMS陀螺儀隨機噪聲包含：量化噪聲（Quantization Noise）、角度隨機游走（AngularRandomWalk）、偏差不穩定性（BiasInstability）、速率隨機游走（RateRandomWall）、速率斜坡（RateRamp）等5種隨機噪聲[10-12]。各種隨機誤差源與Allan方差的關系如式（3）所示：

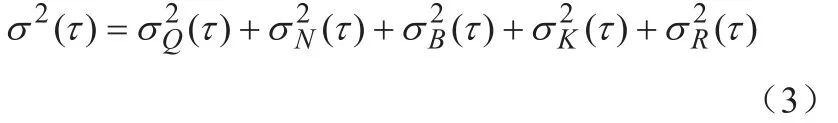
然后用最小二乘法對Allan方差的曲線擬合，可以求得這幾個系數：

MEMS陀螺儀的隨機漂移的誤差的5種隨機誤差的計算公式如表1所示。

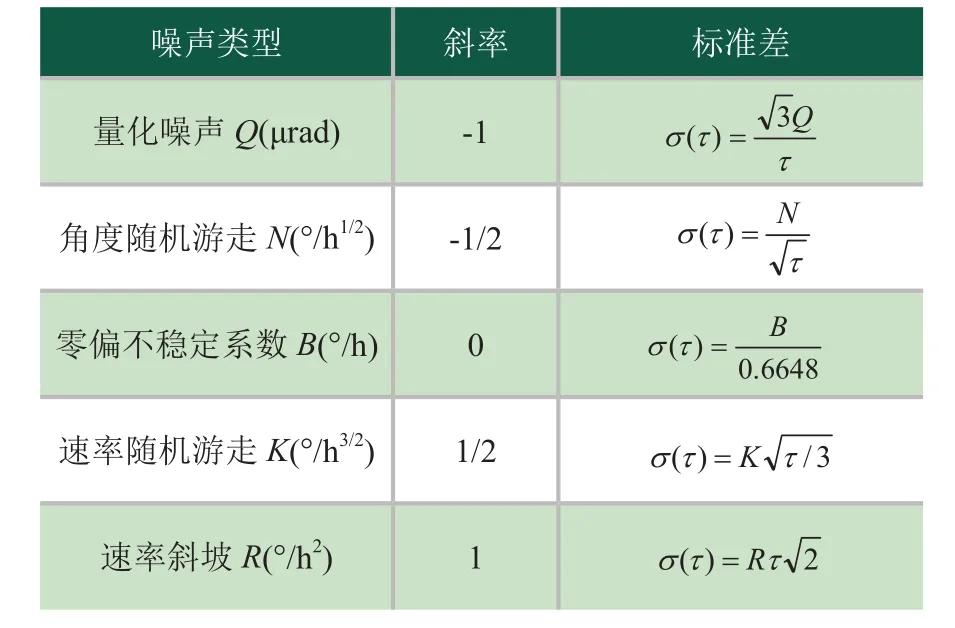
表1 Allen標準差與常見噪聲的對應關系

2、時間序列分析方法與參數估計

如果一個時間序列經過平穩性檢驗后得到一個平穩非白噪聲序列，那么該序列中就蘊含著相關性的信息。在統計學中，通常是建立一個線性模型來擬合該時間序列的趨勢。較為常見的模型有AR、MA、ARMA和ARIMA模型[13]。不同系統生成的隨機序列需要用不同的模型描述，這三種模型之間存在著差異。ARMA模型、AR模型和MA模型的區別在于它們在自相關函數和偏相關函數上反映出不同的特征。AR模型的正則方程是一組線性方程，而MA和ARMA模型的方程一般是非線性。AR模型具有一系列好的性能，因此也是研究最多并且實現廣泛應用的一種模型。

由于陀螺漂移模型階數相對不高，一般不超過3階，所以可以在參數個數不超過3的范圍內的模型進行定階。

本文選擇相對簡單的AR(P)模型。AR(P)表示是p階的自回歸模型，是一種線性的預測，如式（5）所示：

其中，aj—AR(P)模型的自回歸系數；

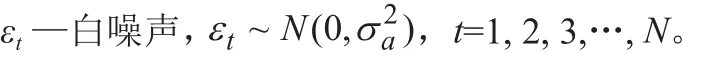
自回歸模型表征的含義是把t時刻測量值由在t時刻之前的p個時間點的測量值的線性擬合與噪聲疊加的輸出結果。

在確定模型之后，就要對陀螺儀漂移模型進行定階。定階的通用方法有BIC準則、AIC準則、FPE準則。本文采用AIC準則，AIC準則中文簡稱為最小信息準則，是由日本數學家赤池弘次提出的。因此，也叫做赤池信息量準則，是估計隨機序列模型階次的一種優良的度量。AIC準則的公式如式（6）所示：

其中，AIC(n)是關于階數n的函數，當AIC(n)的值取最小時，n即為AR模型的階數[13]。

確定好AR模型的階數之后的工作就是對AR模型的參數進行估計，也就是計算其系數與白噪聲。一般選擇最小二乘法對AR模型的參數進行估計，原因是計算簡單、高效并且精度較高，可以滿足計算的需求。最小二乘法進行參數估計的公式為：

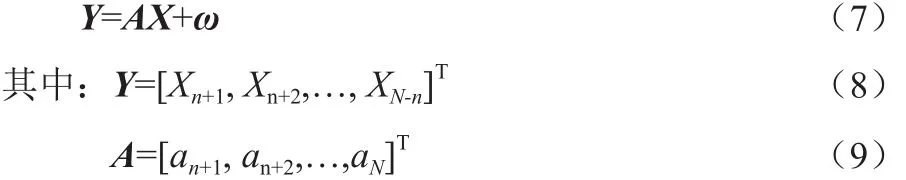
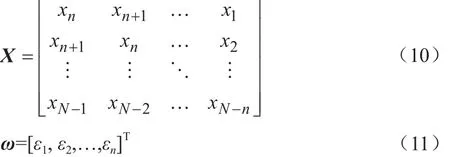
參數估計的公式為：

利用上述公式就可以建立MEMS陀螺儀隨機漂移的模型。

3、經典卡爾曼濾波器

卡爾曼濾波是時域內一種基于最小方差估計的遞推濾波器，將狀態空間的方法引入到了隨機估計理論中，利用系統狀態方程，觀測方程和系統過程噪聲和測量噪聲描述信號系統的輸入輸出[14]，與最小二乘法、維納濾波等用于估計的算法相比其優點如下：

（1）利用狀態空間法進行系統描述，狀態方程能夠描述復雜的多維信號動力學特性，可以避免對信號進行功率譜分解，設計簡單，容易用計算機實現；

（2）不需要保存大量過去的數據，而是通過狀態轉移方程遞推計算出新的估計值；

（3）根據當前測量數據，可以實時遞推計算最優估計值，適用于各種閉環控制系統。

離散隨機系統的卡爾曼狀態方程和測量方程的公式表示為：

其中：Xk—k時刻系統狀態量；

Zk—k時刻系統觀測量；

uk—k時刻系統控制量；

A —系統狀態轉移矩陣；

H —系統量測矩陣；

wk—系統過程噪聲；

vk—系統測量噪聲。

計算k時刻狀態的預測值：

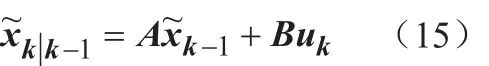
利用k-1時刻狀態最優估計結果，由對k時刻狀態作一步預測，當系統沒有控制量時uk=0。

均方誤差預測為：

其中，Pk-1—一步預測協方差矩陣；

Pk|k-1—上個濾波周期最優估計的協方差矩陣；

Q —狀態噪聲矩陣。

計算濾波增益為：

其中，Kk—卡爾曼增益，表征系統觀測量與一步預測量對于濾波輸出貢獻的大小；

R —k時刻量測噪聲矩陣。

定義k時刻觀測值與其估計值的誤差為新息：

則k時刻卡爾曼濾波輸出的最優估計為：

為下個濾波周期的一步預測做準備，估計的均方誤差：

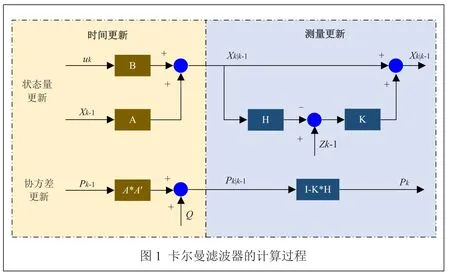
狀態量及協方差的更新如圖1所示。

三、改進的卡爾曼濾波器設計

采用傳統卡爾曼濾波對陀螺儀進行濾波設計時，通常假設系統沒有確定的控制輸入：

即式（21）中uk=0，正是由于這種情況，使得陀螺儀輸出的零點穩定效果不好，不能控制陀螺儀的動態誤差。標準卡爾曼濾波在實際應用時要求有精確的誤差模型和各種噪聲的先驗信息，但通常在許多條件下它們是未知的。使用不精確的模型和噪聲統計特征來設計卡爾曼濾波器可能會產生狀態估計的誤差，甚至會導致濾波發散。

本文在此基礎上增加控制輸入量，即計算一階低通濾波之后的數據y(n)進行差分求取輸入的控制項uk，如下：

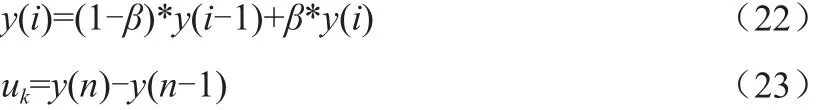
其中，y(i) —當前時刻陀螺儀采樣數據；

y(i-1) —上一時刻陀螺儀采樣數據；

第二，渠道網絡。在中小零售企業電子商務商業運營模式中，企業要將產品或者是服務直接提供到目標客戶，無論應用何種方式，都要建立良好的管理渠道和運行監督管控體系，以便于能在較為適當的時間、地點和人群提供相應的產品以及服務。伴隨著時代的發展和進步，現代渠道具有價值創造的潛力，企業要結合自身的實際需求完善相應的渠道管理機制。

β —低通濾波器系數。

自適應卡爾曼濾波可以利用觀測數據進行遞推，同時實時地對不確定的模型參數和噪聲Q和R的統計特性進行適當的估計和修正，使得模型誤差減小。但相對計算量偏大，增加時間復雜度。因此本文在傳統的卡爾曼濾波器對一步預測方差計算式中增加了一個衰減因子[15]，并且可以在運算速率和提高計算的準確性兩者間獲得平衡。

帶入狀態方程計算k時刻的狀態一步預測：

在傳統卡爾曼濾波器的計算式中加入衰減因子λ，其公式如下：

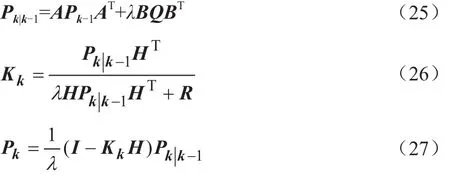
其中，λ為預測方差引入的衰減因子[17-18]，使新數據可以充分參與到估計當中去，λ通常在0～1之間取值，通過對比方差和標準差本文λ取值為0.9。

四、實驗結果與數據分析

為驗證模型可靠性與設計的濾波器的性能，使用單軸ADXRS450水平放在高精度三軸轉臺上，如圖2所示。用電腦連接好數據線串口，接通電源后將陀螺儀保持靜止狀態，預熱30min，等待數據穩定后開始采集陀螺儀數據，時長2h，并截取前30min的角速率數據作為樣本進行分析，對樣本數據進行零均值檢驗，并驗證平穩性和正態性。

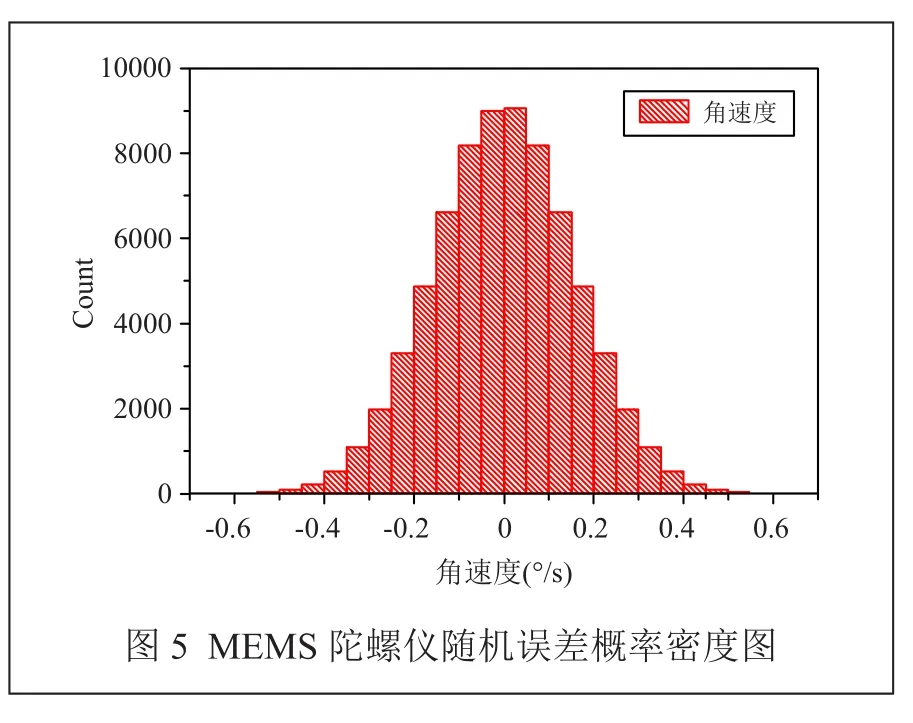
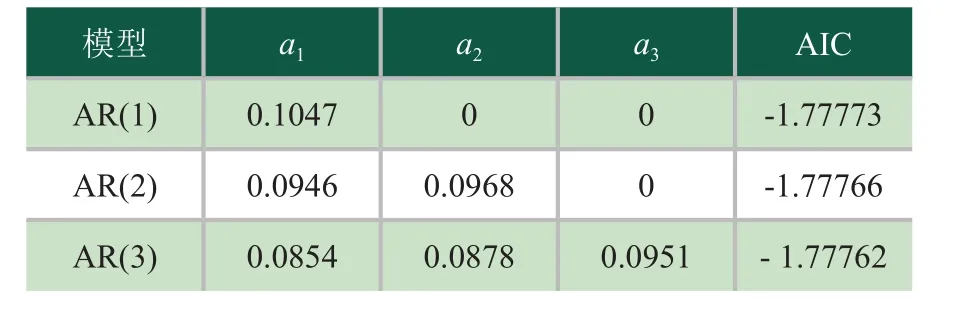
表2 AR模型系數與AIC值

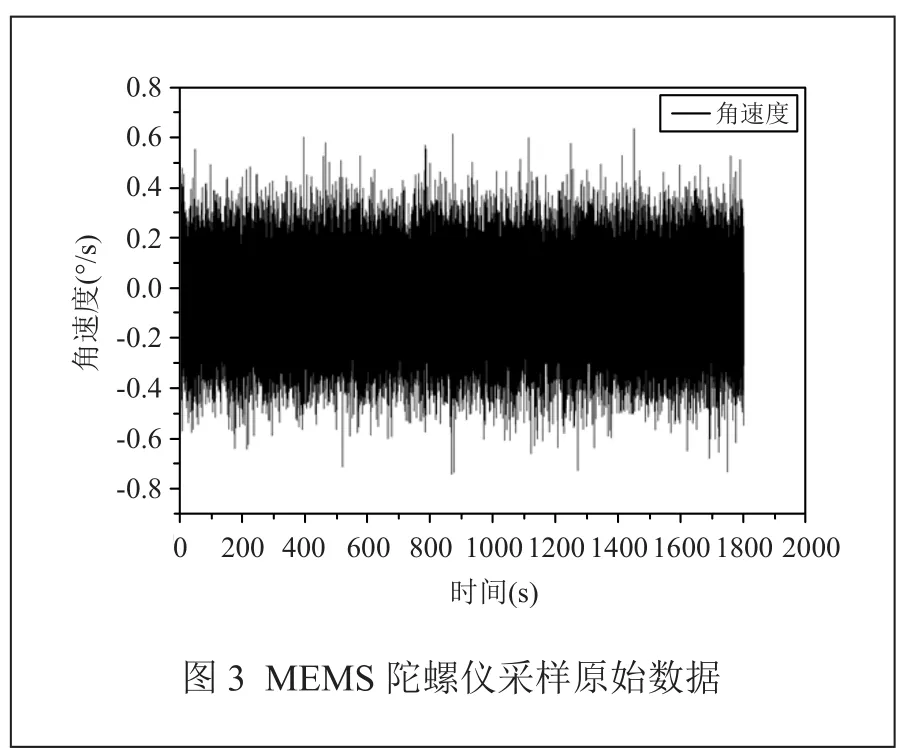
首先，獲取MEMS陀螺儀的隨機信號，通過求取采樣數據平均值得到隨機漂移的常量值，再用采集到的原始數據減去這個值得到如圖3所示。

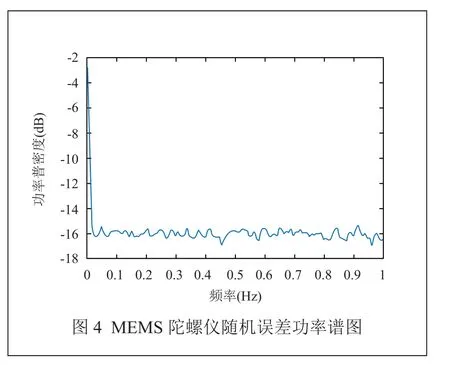
圖4為陀螺儀隨機誤差的功率譜圖。由于陀螺隨機誤差的頻率主要分布在低頻段，沒有明顯的尖峰現象，這意味著陀螺儀信號沒有強周期性，即陀螺隨機誤差中基本沒有明顯的周期分量，滿足平穩性的要求。

圖5為MEMS陀螺儀角速率隨機誤差的概率密度直方圖，由圖可知隨機誤差結果滿足正態性的要求。

驗證之后的建模步驟是：依次以AR(1)、AR(2)、AR(3)模型進行擬合，表2為AR模型擬合系數和AIC計算值。

由表2得出計算的AR模型的AIC最小值為AR(1)模型，因此，本文采用該模型對陀螺儀信號進行模型建立，經過AR(1)模型后的MEMS陀螺儀隨機漂移信號。

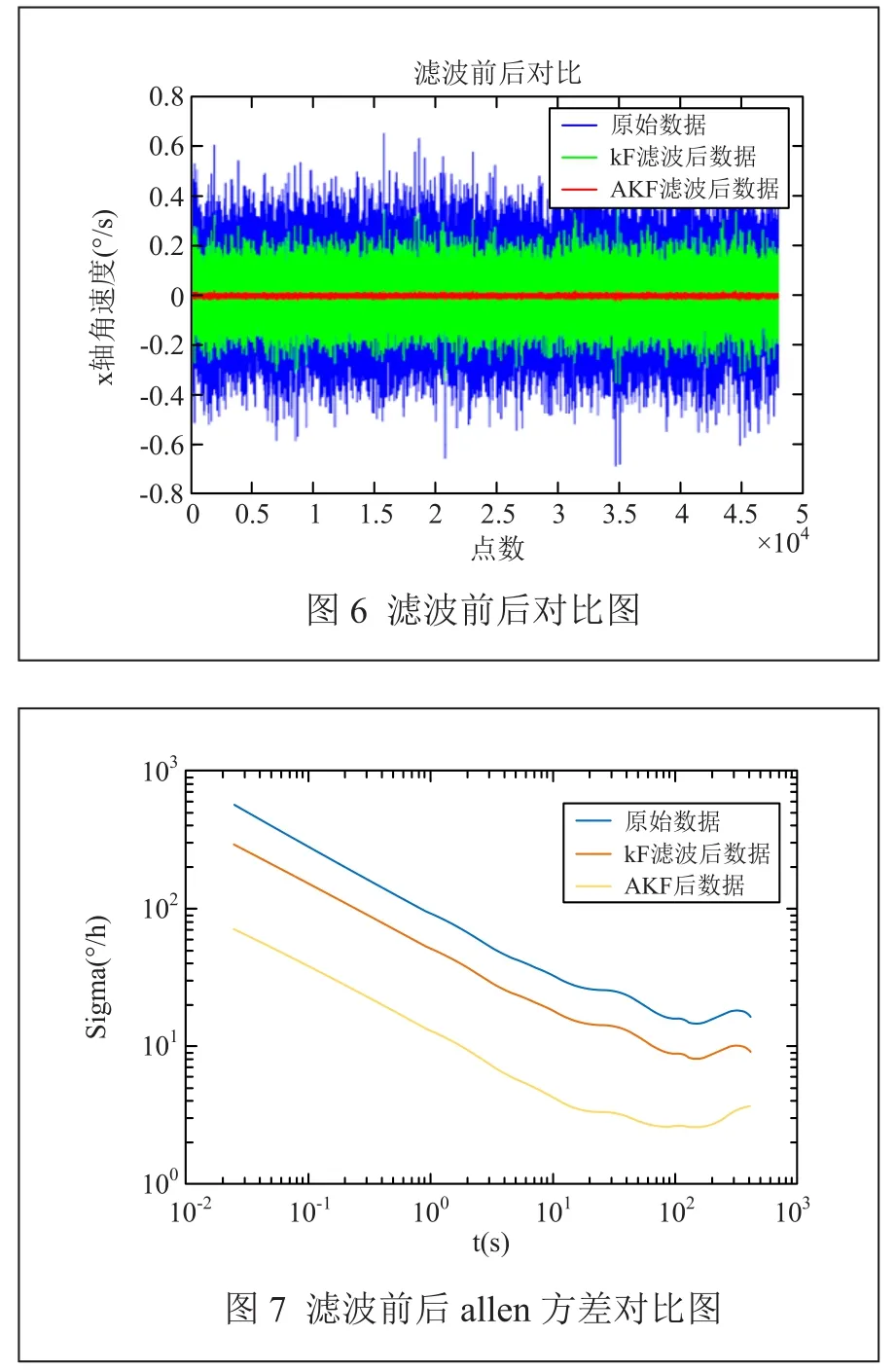
將經典卡爾曼濾波處理后的數據與自適應卡爾曼濾波處理后的效果進行比較，如圖6所示。可以看出經過濾波處理后系統有效信號的隨機量明顯減小，波形更加平穩光滑，說明改進的自適應卡爾曼濾波器能有效的補償MEMS陀螺儀靜態隨機噪聲對系統量測精度的影響，較經典卡爾曼濾波算法濾波效果提升明顯。

采用Allan方差分析法對兩種濾波方法誤差補償后的信號進行辨識分析，兩種濾波方法的方差曲線均整體下移，傳統標準的卡爾曼濾波的濾波效果提升不明顯，而改進的濾波誤差補償算法較傳統算法有較大性能提高，零偏不穩定性經濾波后降低了一個數量級。

濾波前后各指標對比如表3所示。從表中可見原始數據濾波后均值提升1個數量級，方差提升2個數量級，量化噪聲精度提高近1個數量級，角度隨機游走精度提高93.3%，角速率游走提高94.48%。綜上所述，改進的濾波方法對陀螺儀靜態隨機誤差的補償效果顯著。

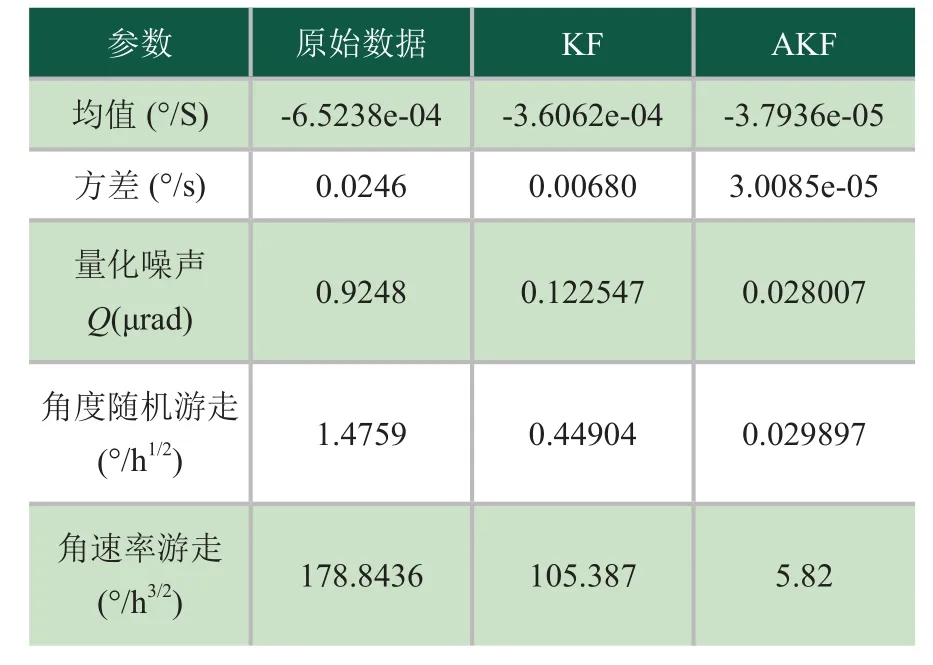
表3 濾波前后各指標對比

五、總結

為了解決低成本MEMS陀螺儀相較于高精度陀螺儀容易受噪聲干擾的問題，本文提出自適應卡爾曼濾波處理方法。首先介紹了用來辨識陀螺儀各種噪聲的Allen方差分析法，對時間序列模型的參數進行估計，并根據AIC準則進行分析定階，進而確定了MEMS陀螺儀模型。在傳統卡爾曼濾波器的基礎上設計了帶衰減因子的自適應卡爾曼濾波器，并引入一階低通濾波后的差分控制項，對MEMS隨機誤差進行補償。實驗結果表明，本文的算法對數據濾波效果明顯，能夠減小隨機噪聲對MEMS陀螺儀靜態性能的影響，提高角速率輸出的精度。