單軸多級(jí)循環(huán)加載下聚氯乙烯膜材料的力學(xué)行為與能量耗散
汪澤幸, 朱文佳, 何 斌, 劉 超
(湖南工程學(xué)院 紡織服裝學(xué)院, 湖南 湘潭 411104)
膜材料由內(nèi)部的增強(qiáng)織物和表層面的涂覆高分子材料構(gòu)成[1],因內(nèi)部增強(qiáng)織物微觀結(jié)構(gòu)的復(fù)雜性、材料與幾何非線性及織造與涂層加工過(guò)程中經(jīng)、緯向張力控制的差異,導(dǎo)致膜材料在不同外加荷載下表現(xiàn)出不同的宏觀力學(xué)行為[2-3]。材料在使用過(guò)程中承受如陣風(fēng)、雨雪的反復(fù)作用及預(yù)加張力的反復(fù)調(diào)整等,膜材料通常處于反復(fù)加載與卸載狀態(tài)。此外,膜材料的變形、強(qiáng)度特征及斷裂損傷力學(xué)特性與所受的應(yīng)力狀態(tài)和加載歷史密切相關(guān),同時(shí),膜材料在不同應(yīng)力條件下的破壞實(shí)際上是內(nèi)部微裂紋、缺陷等在荷載條件下斷裂、擴(kuò)張的宏觀表現(xiàn)。
目前,眾多學(xué)者對(duì)建筑用膜材料為代表的柔性復(fù)合材料在反復(fù)加載下的力學(xué)行為進(jìn)行了較為全面的研究:陳務(wù)軍等[4-7]研究發(fā)現(xiàn)聚四氟乙烯膜材料、取偏氟乙烯/聚醚砜膜材料以及機(jī)織物增強(qiáng)柔性復(fù)合材料的彈性模量、殘余變形與反復(fù)加卸載次數(shù)密切相關(guān);Chen等[8-9]對(duì)浮空器膜材料在單、雙軸循環(huán)下彈性模量的變化趨勢(shì)進(jìn)行研究發(fā)現(xiàn),經(jīng)、緯向應(yīng)力比與彈性模量之間存在耦合關(guān)系,并分析了經(jīng)、緯向應(yīng)力比與耦合彈性模量的影響規(guī)律;Zhang等[10-12]研究發(fā)現(xiàn),循環(huán)加載下PTFE膜材料的單、雙軸拉伸行為主要受應(yīng)力幅值、溫度和增強(qiáng)骨架織物結(jié)構(gòu)的影響,且加載歷史對(duì)力學(xué)行為的影響較為明顯。
但上述研究主要集中于彈性模量以及拉伸曲線線性程度的變化。而對(duì)多級(jí)循環(huán)加載過(guò)程中的能量耗散與演化研究較少。基于此,本文對(duì)多級(jí)循環(huán)加載時(shí)的循環(huán)加載峰值強(qiáng)度、變形特征、彈性力學(xué)性能、斷裂損傷力學(xué)特性等問(wèn)題進(jìn)行研究,對(duì)宏觀力學(xué)行為進(jìn)行闡述和分析,并對(duì)能量耗散及損傷演化進(jìn)行研究,以期深入了解膜材料的破壞力學(xué)行為,為其工程應(yīng)用提供參考。
1 實(shí)驗(yàn)材料與方法
1.1 實(shí)驗(yàn)材料
本文以商購(gòu)?fù)繉臃ㄖ苽涞氖┒魈鼐勐纫蚁?PVC)膜材料為研究對(duì)象,其表層耐氣候?qū)油扛膊牧蠟榫燮蚁?PVDF),增強(qiáng)骨架織物的組織結(jié)構(gòu)為二上二下方平組織,經(jīng)紗與緯紗均為111.1 tex(192 f)高強(qiáng)滌綸長(zhǎng)絲,織物經(jīng)密和緯密均為24根/(5 cm),膜材料實(shí)測(cè)厚度為0.72 mm,面密度為800 g/m2。
1.2 試樣制備與實(shí)驗(yàn)方法
試樣寬度為(50±0.5)mm,長(zhǎng)度為(300±0.5)mm,有效夾持隔距為(200±0.5)mm。多級(jí)循環(huán)加載實(shí)驗(yàn)時(shí),以10 mm/min的速率進(jìn)行自動(dòng)加卸載,循環(huán)峰值應(yīng)力每級(jí)增加5 N/mm,直至試樣斷裂;為確保實(shí)驗(yàn)過(guò)程中,試樣始終處于張拉狀態(tài),卸載下限應(yīng)力為第一級(jí)循環(huán)前的預(yù)加張力,有效實(shí)驗(yàn)樣本數(shù)為3,對(duì)應(yīng)經(jīng)向試樣編號(hào)分別為W-1、W-2與W-3,緯向試樣編號(hào)為F-1、F-2與F-3。為對(duì)比研究多級(jí)循環(huán)加載時(shí)PVC膜材料的強(qiáng)度特性,同時(shí)對(duì)經(jīng)緯向試樣進(jìn)行單軸直接拉伸斷裂實(shí)驗(yàn),加載速度設(shè)定為10 mm/min,有效樣本數(shù)為5。
所有實(shí)驗(yàn)均在室溫下采用型號(hào)為WDW-20的華龍萬(wàn)能強(qiáng)力試驗(yàn)機(jī)進(jìn)行。
2 結(jié)果與分析
2.1 松弛特性分析
PVC膜材料直接拉伸及多級(jí)循環(huán)加載時(shí)的應(yīng)力-應(yīng)變曲線如圖1、2所示。由圖1可知,膜材料經(jīng)、緯向試樣的5次直接拉伸曲線在峰值強(qiáng)度之后應(yīng)力突然跌落,具有突然破壞的特征。多級(jí)循環(huán)加載下,應(yīng)力-應(yīng)變曲線呈現(xiàn)周期性變化,加載與卸載曲線構(gòu)成的滯后環(huán)面積隨著循環(huán)次數(shù)增加而增加(見(jiàn)圖2)。實(shí)驗(yàn)結(jié)果表明,經(jīng)向直接拉伸斷裂強(qiáng)度為85.88 N/mm,多級(jí)循環(huán)平均斷裂峰值強(qiáng)度為76.67 N/mm,較直接拉伸強(qiáng)度(σC)下降9.21%;緯向單軸拉伸斷裂強(qiáng)度為54.78 N/mm,多級(jí)循環(huán)平均斷裂峰值強(qiáng)度為66.67 N/mm,較直接拉伸斷裂強(qiáng)度增加21.71%。

圖1 試樣拉伸斷裂應(yīng)力-應(yīng)變曲線
Fig.2 Fracture stress-strain curves of tested specimens
實(shí)驗(yàn)用PVC膜材料中增強(qiáng)織物的經(jīng)密與緯密一致,織造過(guò)程中為確保梭口清晰,以便織造加工,經(jīng)紗所承受的張力較高,伸直度較好。涂層加工過(guò)程中,經(jīng)向亦承受的張力較大,經(jīng)紗進(jìn)一步伸直,屈曲程度降低,外加載荷作用下,經(jīng)紗強(qiáng)力利用率較高,導(dǎo)致膜材料的經(jīng)向直接拉伸強(qiáng)度較高。
在織造與涂層加工過(guò)程中,經(jīng)紗承受高張力且受反復(fù)拉伸、彎曲、摩擦和沖擊作用,纖維中大分子已充分伸直;多級(jí)循環(huán)加載時(shí),大分子之間產(chǎn)生滑移,導(dǎo)致大分子之間作用力下降,宏觀表現(xiàn)為多級(jí)循環(huán)峰值強(qiáng)度低于直接拉伸斷裂強(qiáng)度。在織造和涂層過(guò)程中,緯紗承受的張力較低且張力波動(dòng)較小,循環(huán)加載作用有利于纖維中大分子的進(jìn)一步伸直,有利于增強(qiáng)承受外加載荷的作用,從而宏觀表現(xiàn)為多級(jí)循環(huán)峰值強(qiáng)度高于直接拉伸斷裂強(qiáng)度。
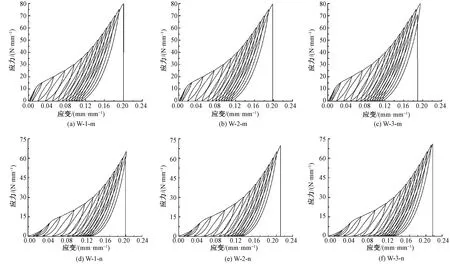
注:m—加載; n—卸載。圖2 多級(jí)循環(huán)加載與卸載下試樣的應(yīng)力-應(yīng)變曲線
Fig.2 Stress-strain curves of tested specimens under multi-level cyclic loading and unloading
2.2 循環(huán)彈性模量分析
循環(huán)加載過(guò)程中,加載和卸載彈性模量的計(jì)算方法主要有線性擬合法和近似等效法2種。線性擬合法:基于加載和卸載應(yīng)力-應(yīng)變曲線的初始階段,對(duì)其線性擬合而獲得加載和卸載彈性模量,該種方法可反映材料的彈性模量特征;近似等效法:基于初始加載點(diǎn)A與加載終點(diǎn)B連線斜率計(jì)算加載彈性模量,基于初始卸載點(diǎn)B(與加載終點(diǎn)同點(diǎn))與卸載終點(diǎn)C連斜率計(jì)算卸載彈性模量,其核心為將加載和卸載曲線近似等效為直線,直線斜率即為加載或卸載彈性模量,此方法計(jì)算簡(jiǎn)便,易于操作(見(jiàn)圖3)。
Fig.3 Level 2 stress-strain curves of W-1 specimen
經(jīng)、緯向試樣的多級(jí)循環(huán)加載與卸載曲線均表現(xiàn)出明顯的非線性特征,加載和卸載彈性模量計(jì)算時(shí),A、B點(diǎn)間連線斜率高于曲線AB初始段的斜率,同時(shí)B、C點(diǎn)連線斜率亦高于曲線BC初始段的斜率。相對(duì)于線性擬合法,基于近似等效法計(jì)算的加載和卸載彈性模量較高,且無(wú)法客觀地反映材料的力學(xué)行為。
因此,本文基于線性擬合法計(jì)算加載和卸載彈性模量,其曲線如圖4所示。 可知,PVC膜材料經(jīng)、緯向試樣的加載及卸載彈性隨循環(huán)加載次數(shù)的增加而增加。同一循環(huán)內(nèi),卸載模量高于加載模量,且隨著循環(huán)次數(shù)的增加,二者之間的差值逐漸增加。
循環(huán)加載下,增強(qiáng)纖維和涂層材料中結(jié)合力較差的大分子鏈間產(chǎn)生滑移,并在新的位置建立新的相互結(jié)合,且大分子鏈的伸直程度增加,受力同時(shí)性提高,纖維變形主要由大分子鏈段的伸長(zhǎng)和回縮產(chǎn)生,宏觀上表現(xiàn)為彈性模量的增加。
2.3 能耗耗散特征
圖3中:曲線AB下方區(qū)域ABFEA面積為總吸收應(yīng)變能,表示一個(gè)加載與卸載循環(huán)過(guò)程中外力對(duì)試樣所做的功;曲線BC下方區(qū)域CBFDC面積為該循環(huán)的彈性應(yīng)變能;區(qū)域ABCDEA的面積為耗散能,用于試樣損傷及塑性變形,總吸收應(yīng)變能、彈性應(yīng)變能與耗散能間的關(guān)系可表示為:
Ud=U-Ue
(1)

圖4 加載與卸載彈性模量曲線
Fig.4 Elastic modulus curves. (a) Warp specimens; (b) Fill specimens
式中:U為總應(yīng)變能,mJ/mm3;Ue為彈性應(yīng)變能,mJ/mm3;Ud為耗散能,mJ/mm3。
加載與卸載曲線不重合,形成滯后環(huán),這主要是由于PVC膜材料為典型的黏彈性材料所致;多級(jí)循環(huán)加載時(shí),材料產(chǎn)生塑性變形,因此,形成的滯后環(huán)并未封閉。
試樣總吸收應(yīng)變能、彈性應(yīng)變能及耗散能的變化趨勢(shì)如圖5所示。可看出,經(jīng)、緯向試樣的能量變化曲線形態(tài)相似且呈現(xiàn)非線性增長(zhǎng)趨勢(shì),表明多級(jí)循環(huán)加載下經(jīng)、緯向試樣的能量吸收、儲(chǔ)存與耗散的機(jī)制是一致的。

圖5 能量變化與應(yīng)力和歸一化應(yīng)力關(guān)系曲線
Fig.5 Energy variation curves with stress and normalized stress. (a) Total absorption strain energy with stress; (b) Elastic strain energy with stress; (c) Dissipated energy varied with stress; (d)Total absorption strain energy with normalized stress; (e) Elastic strain energy with normalized stress; (f) Dissipated energy varied with normalized stress
同等循環(huán)載荷峰值時(shí),經(jīng)向試樣具有較低的總吸收應(yīng)變能量、彈性應(yīng)變能和耗散能。以經(jīng)向試樣W-1、緯向試樣F-1的第2個(gè)加載循環(huán)(見(jiàn)圖6)為例,因經(jīng)向試樣的加載和卸載模量較高,達(dá)到同等循環(huán)載荷峰值時(shí),經(jīng)向試樣的初始加載應(yīng)變(εloading)和卸載應(yīng)變(εunloading)較小,故加載和卸載曲線下方的面積較小,即總吸收應(yīng)變能和彈性應(yīng)變能較小;同時(shí),因同一循環(huán)過(guò)程中,經(jīng)向試樣產(chǎn)生的塑性形變(εunloading-εloading)也較小,在加、卸載模量差異以及塑性變形差異的雙重作用下,經(jīng)向試樣的耗散能也較低。

圖6 經(jīng)典試樣的第一及二級(jí)應(yīng)力-應(yīng)變曲線
Fig.6 First and second levels stress-strain curves of typical tested samples
由圖5(a)~(c)可知,在同級(jí)加載循環(huán)中,相對(duì)于經(jīng)向試樣,緯向試樣的總吸收應(yīng)變能、彈性應(yīng)變能和耗散能較高,與緯向試樣彈性模量和強(qiáng)度較低的結(jié)論不吻合。
圖5(d)~(f)示出,同級(jí)加載循環(huán)對(duì)于經(jīng)、緯向試樣是處于不同應(yīng)力階段的,就第3加載循環(huán)而言,經(jīng)向試樣W-1的峰值應(yīng)力與緯向試樣相差較大,因此同級(jí)加載循環(huán)的經(jīng)、緯向試樣能量對(duì)比不能真實(shí)反映材料的能量變化過(guò)程,而應(yīng)力歸一化后的分析結(jié)果較為可靠。圖5(d)~(f)表明:當(dāng)循環(huán)峰值載荷水平較高時(shí),經(jīng)向試樣的總吸收應(yīng)變能、彈性應(yīng)變能和耗散能相對(duì)較高;而當(dāng)循環(huán)峰值載荷水平較低時(shí),緯向試樣的總吸收應(yīng)變能、彈性應(yīng)變能和耗散能相對(duì)較高。
循環(huán)載荷峰值水平較低時(shí),能量的吸收、儲(chǔ)存主要依靠增強(qiáng)織物結(jié)構(gòu)的變化、紗線和涂層材料大分子構(gòu)象的變化來(lái)實(shí)現(xiàn);而能量的耗散主要源自增強(qiáng)纖維和涂層材料中大分子鏈的滑移、原有損傷的擴(kuò)展、涂層和增強(qiáng)纖維之間結(jié)合點(diǎn)的破壞等。因織造和涂層加工過(guò)程中張力的差異,相對(duì)于經(jīng)紗,緯紗伸直程度較小且紗線中大分子鏈段伸展程度不充分,在外加荷載下,緯紗的伸長(zhǎng)主要由緯紗屈曲程度減小和大分子鏈段伸直、滑移構(gòu)成,緯紗伸長(zhǎng)導(dǎo)致模量較低,從而使緯向試樣表現(xiàn)出較高的總吸收能;回復(fù)階段,伸直大分子鏈段向初始狀態(tài)回復(fù),紗線屈曲狀態(tài)變化,緯紗屈曲程度較高,對(duì)能量的儲(chǔ)存能力較強(qiáng)。在循環(huán)加載過(guò)程中,原有弱損傷得以破壞且因緯紗屈曲結(jié)構(gòu)變化較大,增強(qiáng)纖維與涂層材料之間黏結(jié)點(diǎn)破壞概率較高且數(shù)量較多,宏觀表現(xiàn)為耗散能的增加。
循環(huán)載荷峰值水平較高時(shí),能量的吸收、儲(chǔ)存和耗散主要依賴增強(qiáng)纖維和涂層材料中大分子鏈的伸直、回復(fù)與滑移。荷載比例越高,大分子鏈段的伸直程度越高,滑移程度越大,數(shù)量越多,同時(shí)可回復(fù)能力也提高。
2.4 能量耗散率變化規(guī)律
將耗散能Ud對(duì)總吸收應(yīng)變能U的比值定義為能量耗散率u,即
(2)
圖7示出能量耗散率的變化曲線。可以看出,隨著循環(huán)載荷峰值的增加,經(jīng)、緯向試樣的能量耗散率呈非線性變化,總體呈現(xiàn)先增加后降低的變化趨勢(shì)。在加載初期,耗散能Ud占比較低,大部分吸收的能量轉(zhuǎn)化為彈性應(yīng)變能Ue,表明材料內(nèi)部缺陷的擴(kuò)張、增強(qiáng)纖維和涂層材料中大分子鏈滑移、增強(qiáng)纖維和涂層材料之間脫黏等消耗的能量相對(duì)較少,主要轉(zhuǎn)化為可回復(fù)的彈性應(yīng)變能Ue;隨著循環(huán)荷載峰值增加,耗散能量Ud增加,同時(shí)能量耗散率增加,并在循環(huán)荷載為20 N/mm時(shí)達(dá)到極大值;當(dāng)循環(huán)荷載峰值超過(guò)此臨界值后,雖然耗散能繼續(xù)增加(見(jiàn)圖5),但大部分能量轉(zhuǎn)化為彈性應(yīng)變能Ue,能量耗散率呈現(xiàn)逐漸降低的變化趨勢(shì)。從能量耗散率的角度分析,PVC膜材料使用強(qiáng)度控制在20 N/mm以下較為合理。

圖7 能量耗散率變化曲線
Fig.7 Variation curves of energy dissipation rate withstress (a) and normalized stress (b)
從圖7還可以看出,對(duì)于第1級(jí)循環(huán)加卸載過(guò)程中,緯向試樣的能量耗散率較高,這仍然與織造和涂層加工過(guò)程中,經(jīng)緯向所處的張力狀態(tài)存在差異有關(guān)。
2.5 損傷變量的定義與分析
Lemaitre等[13]從彈性模量變化的角度定義損傷變量,即以彈性模量為損傷因子,認(rèn)為可利用損傷試樣與無(wú)損試樣的彈性模量之比來(lái)定義損傷變量DE,即
DE=1-E′/E
(3)
式中,E、E′分別為無(wú)損傷材料與損傷材料的彈性模量,N/mm。
損傷體現(xiàn)為材料缺陷產(chǎn)生、擴(kuò)展,在此過(guò)程中,彈性模量將呈現(xiàn)逐漸降低的變化趨勢(shì);當(dāng)材料完全損傷時(shí),材料發(fā)生完全破壞,此時(shí)彈性模量E′為0,即材料的損傷變量極限為1.0。
由圖5可知,隨著多級(jí)循環(huán)加載的進(jìn)行,PVC膜材料的彈性模量呈現(xiàn)出遞增的變化趨勢(shì),故基于彈性模量變化而獲得的損傷變量將不可避免出現(xiàn)負(fù)值,即材料表現(xiàn)為“負(fù)損傷”,計(jì)算獲得的損傷變量值與實(shí)際損傷演化特征相矛盾,所以在多級(jí)循環(huán)加載條件下,采用彈性模量作為損傷因子的方法是不合理的。
循環(huán)加載時(shí),材料可能出現(xiàn)2類(lèi)破壞極限:1)材料處于彈性工作狀態(tài)時(shí),循環(huán)加載作用下,材料雖不產(chǎn)生塑性變形,但微量損傷在材料結(jié)構(gòu)內(nèi)部產(chǎn)生、累積,當(dāng)這些微量損傷累積達(dá)到一定程度時(shí),材料達(dá)到破壞極限,發(fā)生疲勞破壞;2)材料處于彈塑性工作狀態(tài)時(shí),循環(huán)加載將引起材料產(chǎn)生塑性變形并累積,當(dāng)這些累積塑性變形超過(guò)一定程度時(shí),會(huì)弱化材料的使用性能,直至出現(xiàn)破壞極限。
從能量轉(zhuǎn)換的角度而言,損傷的累積意味著能量的耗散,因而可從能量耗散的角度定義損傷變量,故可將各循環(huán)加載過(guò)程中累積的耗散能與最后一級(jí)加載循環(huán)的總應(yīng)變能比值定義為損傷變量DU,即循環(huán)加載到第i級(jí)時(shí)損傷變量DU(i)可表示為:
(4)
式中,U(t)為最后一級(jí)循環(huán)的總應(yīng)變能,mJ/mm3。
基于式(4)計(jì)算而得的損傷變量與循環(huán)級(jí)數(shù)之間的關(guān)系見(jiàn)圖8。可以看出,循環(huán)加載次數(shù)約超過(guò)7次后,經(jīng)、緯向試樣損傷變量值均大于1.0,與損傷極限為1.0矛盾,故采用式(4)計(jì)算損傷變量也不適用。

圖8 損傷變量DU與循環(huán)次數(shù)曲線
Fig.8 Curves of damage variableDUand cycle number
由圖2、3和6可知,PVC膜材料的加載和卸載曲線并不重合且構(gòu)成的滯后環(huán)也不封閉,從而表明在整個(gè)多級(jí)循環(huán)加載過(guò)程中,PVC膜材料均處于彈塑性工作狀態(tài),循環(huán)加載將引起塑性變形的累積,從而導(dǎo)致材料性能的劣化,基于此,可定義損傷變量為各加載循環(huán)累積的塑性應(yīng)變與無(wú)損試樣(直接拉伸試樣)斷裂應(yīng)變之比,即加載到第i級(jí)循環(huán)時(shí)損傷變量Dε(i)可表示為:
(5)
式中:εb為單向拉伸時(shí)試樣的斷裂應(yīng)變,mm/mm;εper為各循環(huán)產(chǎn)生的塑性變形,mm/mm。
基于式(5)計(jì)算而得的損傷變量Dε與循環(huán)加載次數(shù)之間的變化關(guān)系如圖9所示。

圖9 損傷變量Dε與循環(huán)次數(shù)曲線
Fig.9 Curves of Damage variableDεand cycle number
從圖中可以看出,基于塑性變形累積而計(jì)算獲得的損傷變量Dε值在0~1之間,在損傷極限范圍之內(nèi)可認(rèn)為,基于塑性變形累積來(lái)定義損傷變量較為合理;同時(shí)發(fā)現(xiàn),在隨著多級(jí)循環(huán)加載的進(jìn)行,經(jīng)、緯向試樣的損傷均呈現(xiàn)相似的非線性增長(zhǎng)趨勢(shì),表明PVC膜材料經(jīng)、緯向的損傷機(jī)制相似,且同等循環(huán)荷載峰值條件下,緯向試樣的損傷程度高于經(jīng)向試樣。
3 結(jié) 論
本文對(duì)PVC膜材料在單軸加載下的多級(jí)循環(huán)和直接拉伸性能進(jìn)行了測(cè)試和分析,研究了多級(jí)循環(huán)加載下PVC膜材料的變形行為及機(jī)制,分析了PVC膜材料在多級(jí)循環(huán)加載下的損傷特性,實(shí)驗(yàn)分析結(jié)果如下。
1)本文選用的PVC膜材料,其經(jīng)向試樣的多級(jí)循環(huán)斷裂峰值強(qiáng)度低于直接拉伸強(qiáng)度,而緯向試樣高于直接拉伸強(qiáng)度,這主要因?yàn)榭椩旌屯繉蛹庸み^(guò)程中經(jīng)緯向紗線所承受的張力差異。
2)因PVC膜材料的加載和卸載曲線呈現(xiàn)明顯的非線性,因而相對(duì)于近似等效計(jì)算方法,采用線性擬合法來(lái)獲取加卸載模量較為合理。隨多級(jí)循環(huán)加載的進(jìn)行,加載和卸載彈性模量總體表現(xiàn)出遞增的變化趨勢(shì),且卸載彈性模量高于加載彈性模量。
3)由于多級(jí)循環(huán)加載的峰值強(qiáng)度與循環(huán)加卸載次數(shù)不同,經(jīng)、緯向試樣在相同循環(huán)加載次數(shù)時(shí),其各自的變形過(guò)程處于不同階段。能量與歸一化應(yīng)力變化趨勢(shì)表明,小載荷水平下,相對(duì)于經(jīng)向試樣,緯向試樣的總吸收應(yīng)變能、彈性應(yīng)變能和耗散能較高,但在高載荷水平下較低。
4)多級(jí)循環(huán)加載時(shí),PVC膜材處于彈塑性變形階段,相對(duì)于基于彈性模量變化和耗散能累積定義損傷變量,基于塑性變形累積來(lái)定義損傷變量較為合理。
FZXB

