基于SAPSO-FNN的電動式加載系統控制研究

高超，白國振，周同，馮春華

(上海理工大學機械工程學院，上海200093)

蝸輪蝸桿機構作為一種機械裝置，廣泛用于汽車、船舶、建筑用重型機械中。蝸輪蝸桿傳動裝置結構緊湊、減速比較大、工作狀態較平穩、噪聲污染較小且具有一定的自鎖性[1]，因此承載能力成為其主要性能要求之一，同時在一些特殊工況下，例如： 高速、重載等情況下，系統的質量、體積、振動等均為參考指標。在蝸輪蝸桿減速器設計完成后，有必要通過測試來驗證減速器整體是否符合實際使用要求。

為了模擬實際工況，需要使用外部設備來模擬負載，常見的加載系統有： 傳統機械式加載系統、電液式加載系統、電動式加載系統。本文選用電動式加載系統，該系統屬于被動式加載系統，具有結構簡單、質量輕、體積小、控制方便等突出特點，但由于自身轉矩較小，大部分電動式加載系統采用減速器來增大輸出轉矩，從而引入了摩擦，間隙等非線性環節，這些都會對系統的控制精度帶來影響。如何通過合理的控制策略來提高控制精度成為目前電動式加載系統領域研究的課題之一。

針對上述問題，近些年出現了許多關于電動式加載系統的控制方案。文獻[2]針對H∞混合靈敏度優化設計問題，提出了一種基于系統動態跟蹤性能的加權函數確定方法。文獻[3]設計了一種模糊自適應PID控制器，優化了PID參數，提高了電動式加載系統的加載精度。

本文將模糊控制、神經網絡控制、增量式PID控制相結合，設計出一種模糊神經網絡PID控制器。該控制器在保持增量式PID結構簡單的同時，有效地避免了神經網絡在訓練過程中的“黑箱”問題[4]，并且還克服了存在于模糊邏輯的主觀因素。但模糊神經網絡控制收斂速度慢，有陷入局部最優的問題，且初始參數對控制器的控制效果影響較大，針對這些問題，專家學者采用了各種尋優算法，如魚群算法，遺傳算法等用于解決初始值優化的問題[5]。本文中采用了基于模擬退火的粒子群算法優化算法訓練模糊神經網絡的控制參數。

基于模擬退火的粒子群算法在保留了粒子群算法優點的同時，繼承了模擬退火算法在搜索過程中具有概率突跳的能力，能夠有效避免搜索過程陷入局部最優解，使得整個控制器初始參數近似最優解。

1 蝸輪蝸桿疲勞試驗臺的建模

1.1 蝸輪蝸桿疲勞試驗臺

本文所用電動式加載系統控制研究是在蝸輪蝸桿疲勞試驗臺上進行的。疲勞試驗臺的硬件組成包括加載電機、負載電機、扭矩傳感器、聯軸器、蝸輪蝸桿減速器、驅動器及配套組件、I/O模塊、工控機等[6]。

1)在加載電機側，使用TwinCAT3軟件將扭矩加載信號經過模擬量輸出模塊輸出至拓展模塊的模擬量輸入端子中[7]，控制系統根據拓展模塊所接收到的模擬量信號控制加載電機輸出轉矩，扭矩傳感器將扭矩信號通過模擬量輸入模塊實時反饋給TwinCAT3軟件，將加載信號與反饋信號進行對比，獲得誤差，并在TwinCAT3軟件中通過控制算法得到控制量，實現反饋信號趨近于加載信號。

2)在負載電機側，使用TwinCAT3軟件將速度信號通過模擬量輸出模塊輸出至拓展模塊的模擬量輸入端子中，控制系統根據拓展模塊所接收到的模擬量信號控制負載電機輸出轉速，同時電機編碼器將電機位置信號通過拓展模塊中編碼器端子輸出至編碼器模塊中，并實時反饋給TwinCAT3軟件中，從而在TwinCAT3軟件中使用配軸的形式完成位置閉環。

1.2 加載系統的建模

試驗臺整體系統結構如圖1所示，根據試驗臺系統結構，并將扭矩傳感器1模型帶入后，可得圖2所示的系統開環結構框圖[8]。

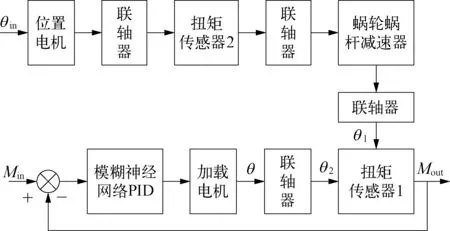
圖1 試驗臺整體系統結構示意

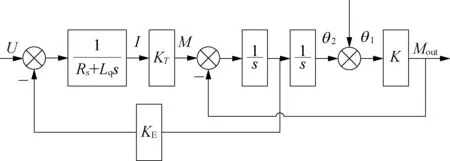
圖2 系統開環結構示意

由圖2可知，加載系統以電壓指令U與負載端角度θ1為輸入，以加載電機實際輸出加載扭矩M為輸出，系統的開環傳遞函數為

M(s)=G1(s)U(s)+G2(s)θ1(s)

(1)

(2)

(3)

式中：K——扭矩傳感器1剛度系數；KM——加載電機扭矩常數；KE——加載電機反電動勢常數；L——電機勵磁電感；Rs——電機定子電阻；J——電機軸轉動慣量。

G1(s)為加載系統根據輸入的電壓指令所產生的扭矩，而G2(s)為位置端運動的速度變化所產生的多余扭矩。本文所研究的內容主要是如何實現加載端的扭矩跟隨實時性，不考慮位置端的運動，即研究目標系統開環傳遞函數。傳遞函數中各參數見表1所列。

表1 開環傳遞函數參數

將表1參數帶入式(2)中得到實際控制對象的傳遞函數為

(4)

(5)

2 模糊神經網絡控制器設計

本文所設計的基于模擬退火的粒子群-模糊神經網絡PID控制器結構如圖3所示。

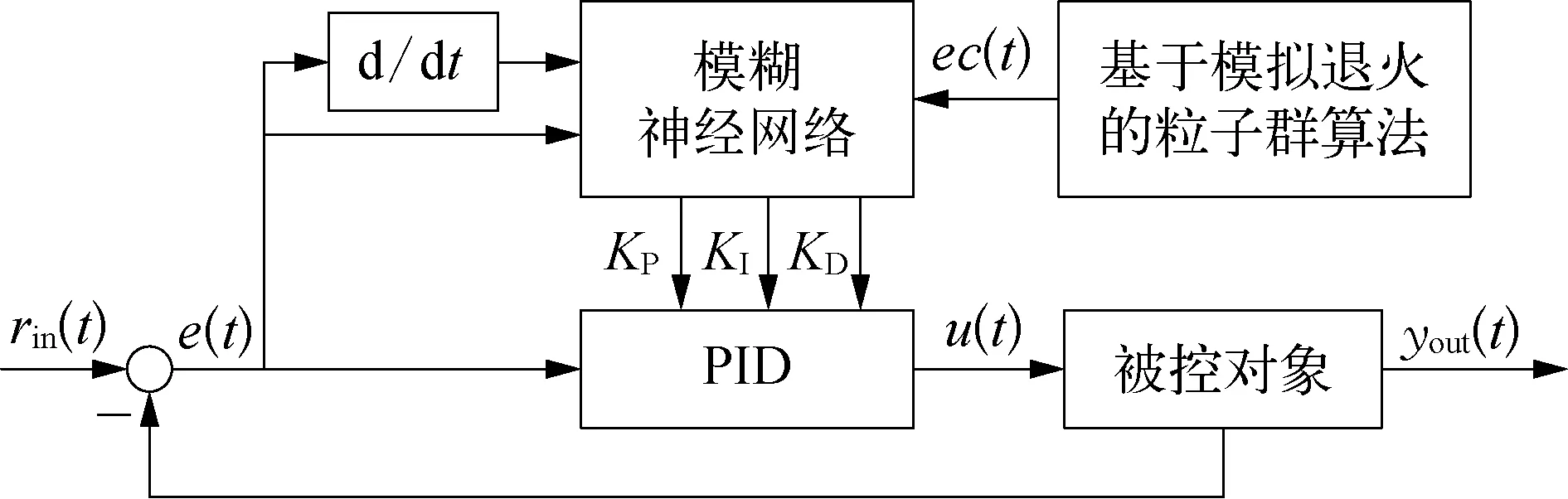
圖3 基于模擬退火的粒子群-模糊神經網絡PID控制器結構示意

圖3中rin(t)為t時刻的輸入扭矩信號，u(t)為t時刻PID控制器輸出控制量信號，yout(t)為t時刻的電機輸出扭矩信號。模糊神經網絡采用“雙輸入三輸出”結構[9]： 輸入為e(t)，ec(t)，其中e(t)表示t時刻的扭矩信號誤差值，ec(t)扭矩信號誤差變化率；KP，KI，KD分別為增量式PID控制參數。

2.1 增量式PID控制原理

PID控制作為一種常用的控制算法，其控制器輸出為[10]

(6)

式中：KP——比例系數；KI——積分系數；KD——微分系數。

在實際應用中，由于計算機控制屬于采樣控制，需要將上式離散化，得到增量式PID控制算法，其控制規律如下：

u(t)=u(t-1)+Δu(t)

(7)

Δu(t)=KP(e(t)-e(t-1))+KIe(t)+

KD(e(t)-2e(t-1)+e(t-2))

(8)

式中：KI=KP/TI；KD=KPTD。

PID控制器的控制效果由KP，KI，KD決定，傳統的PID控制器采用手動的方法進行調節，該方法受操作者的調節經驗影響，且耗時耗力。

2.2 模糊神經網絡

本文所用的模糊神經網絡為基于Mamdani 模型的模糊神經網絡[11]，結構如圖4所示，各層節點功能分述如下。

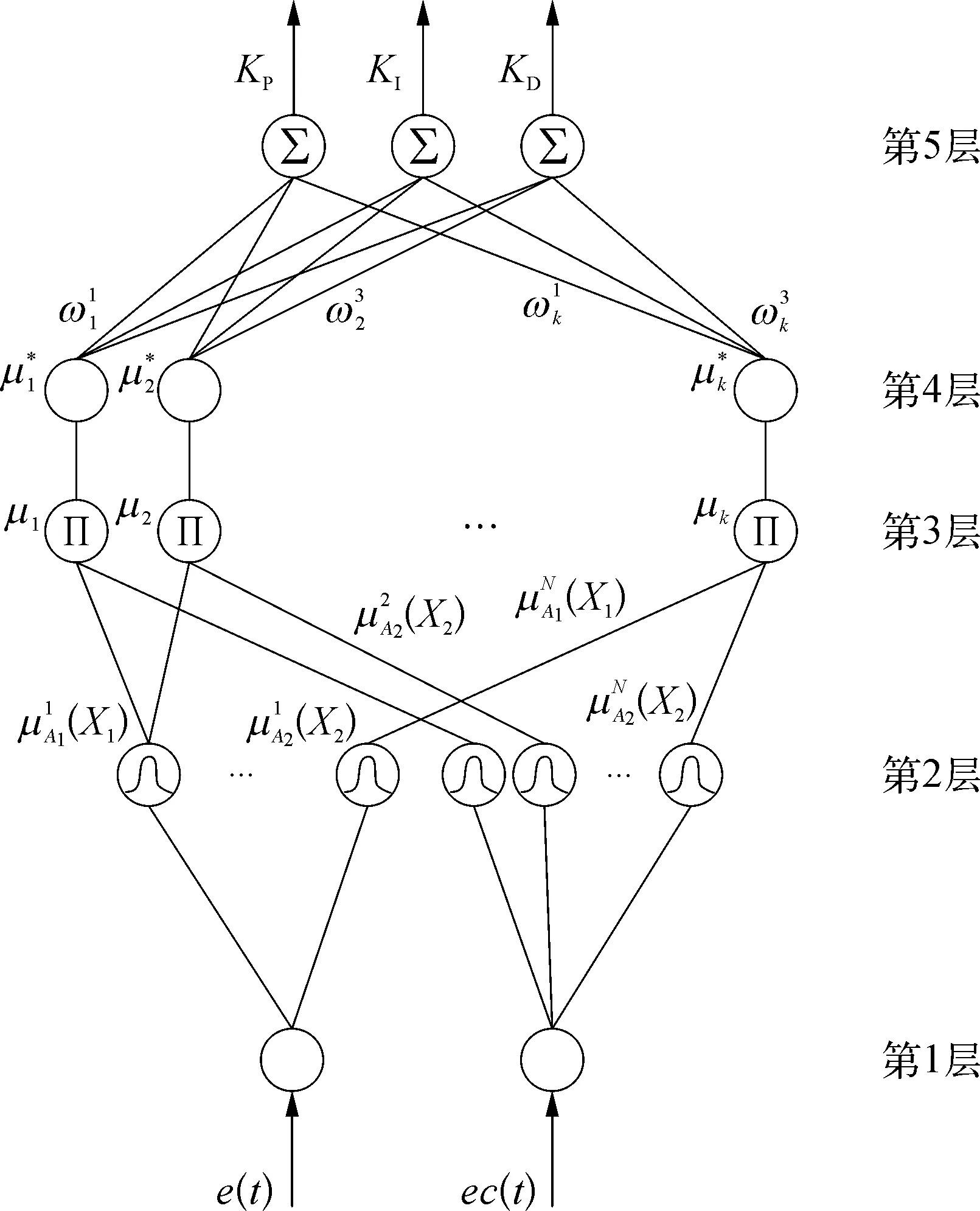
圖4 模糊神經網絡結構示意

2.2.1輸入層

第1層為輸入層，其中節點為輸入節點，每個節點與輸入變量相連接，該層中節點功能僅為將輸入信號傳遞至下一層。在本文中，輸入變量為X1=e(t)(扭矩信號誤差值)，X2=ec(t)(扭矩信號誤差變化率)。

2.2.2隸屬度函數層

第2層為隸屬度函數層，其中節點功能為對第1層輸入變量進行模糊處理，該層的單個節點表示輸入變量的1個模糊子集及對應隸屬度函數，本文中所選用的隸屬度函數為高斯函數：

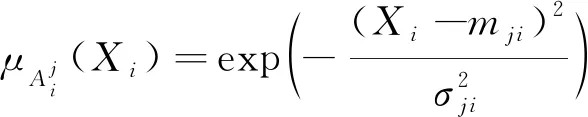
(9)

式中：mji，σji——輸入變量Xi的第j個隸屬度函數(高斯函數)的均值與標準差；N——每個輸入的模糊子集個數。

2.2.3模糊推理層

第3層為模糊推理層，其中每個節點代表了1條模糊規則的前件，該層中每個節點本質上為1個乘法器，將輸入信號相乘，并且輸出乘積結果。

模糊規則如式(10)所示：

(10)

k=1， 2， …，N2
j1=1， 2， …，N
j2=1， 2， …，N

式中：μk——第k條模糊規則輸出。

2.2.4歸一化層

第4層進行歸一化運算，調整網絡整體結構。

(11)

(12)

2.2.5輸出層

第5層為輸出層，使用重心法解模糊，該層輸出即為增量式PID控制器中的KP，KI，KD。

(13)

2.3 模糊神經網絡在線學習方法

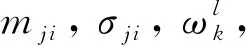
(14)

使用BP算法可將性能指標函數降至最小。

各參數學習公式如式(15)～式(17)所示：

(15)

(16)

(17)

式中：η——學習速率；α——動量因子。

3 基于模擬退火的粒子群算法

3.1 基本粒子群算法

粒子群優化算法—PSO(particle swarm optimization)算法是一種進化計算技術，由Eberhart博士與Kennedy博士于1995年發明[13]，該算法源于對鳥群捕食的行為進行研究，PSO算法與遺傳算法相類似，是一種基于迭代的優化算法。

該算法在N維可行解空間中初始化m個粒子X=(X1，X2，X3， …，Xm)，每個粒子都代表極值優化問題的一個潛在最優解，粒子根據當前的最優粒子在可行解空間中搜索，通過迭代找到最優解，假設n維空間中第i個粒子位置為Xi=(xi1，xi2，xi3， …，xin)，飛行速度Vi=(vi1，vi2，vi3， …，vin)，每個粒子將搜索過程中最優位置記為pbest，Pi=(pi1，pi2，pi3， …，pin)，將整個粒子群中最優位置記為gbest，Pg即指gbest是pbest中的最優值，每次迭代過程中每個粒子通過對應的pbest與gbest的值，再根據式(18)～式(19)來更新自己的位置與速度。

vij(t+1)=vij(t)+c1r1[pij-xij(t)]+
c2r2[pgj-xij(t)]

(18)

xij(t+1)=xij(t)+vij(t+1)
i=1， 2， …，m
j=1， 2， …，n

(19)

式中：c1，c2——正的學習因子或加速度因子；r1，r2——均勻分布于[0， 1]內的隨機數。

3.2 基于模擬退火的粒子群算法

由于粒子群算法存在陷入局部最優的問題，本文選用模擬退火粒子群算法(SAPSO)進行改進。

SAPSO算法在搜索過程中會以概率接受較差的解，這種概率受到溫度參數的控制，隨著溫度的下降而減小，能夠有效地跳出在搜索過程中陷入的局部最小值。

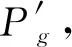
(20)

退火溫度按照式(21)更新：

Tt+1=λTt

(21)

式中：f(Pg)——當前整體最優值Pg的適應度值；λ——退火常數。

根據式(22)計算出當前溫度Tt下各個Pi的適配值：

(22)

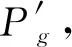
vij(t+1)=χ{vij(t)+c1r1[Pij-xij(t)]+c2r2[P′gj-xij(t)]}

(23)

xij(t+1)=xij(t)+vij(t+1)

(24)

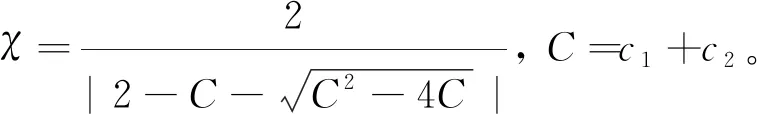
更新各粒子的速度與位置后，根據式(21)更新退火溫度。

3.3 優化算法適應度函數

兩種粒子群算法的適應度函數如式(25)所示：

(25)

式中：e(i)——系統誤差；u2(i)——控制量的平方；tr——上升時間；ω1，ω2，ω3，ω4——權重系數，其中ω4為防止系統超調量過大所采取的懲罰因子。

本文中：

(26)

3.4 算法優化流程

使用SAPSO算法表示本文所設計的結合模擬退火、基本粒子群算法、模糊神經網絡的控制器。其基本流程如圖5所示。

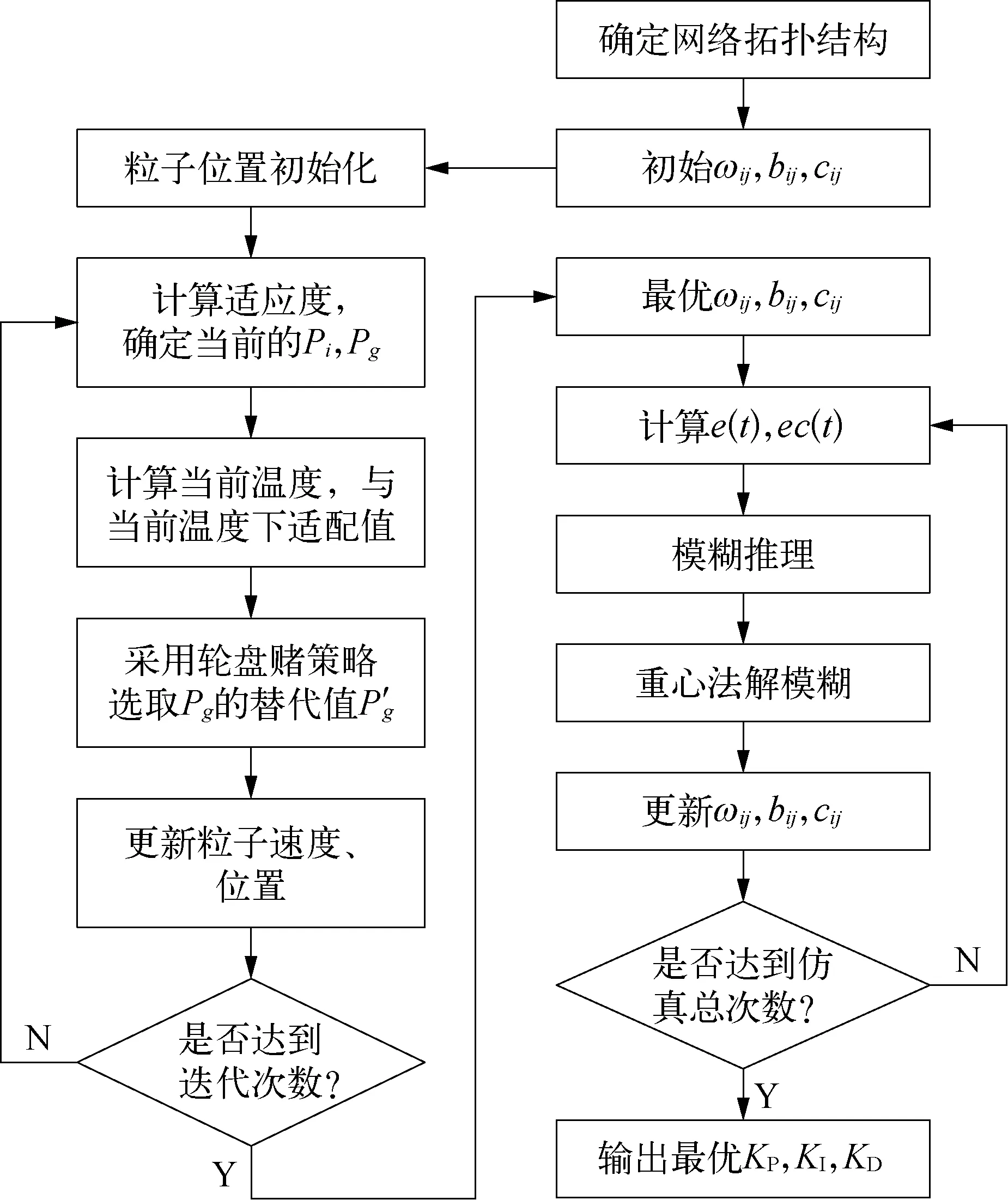
圖5 SAPSO算法基本流程示意

4 仿真與實驗

通過Matlab對蝸輪蝸桿試驗機的加載部分進行仿真，利用SAPSO算法和PSO算法[14]對模糊神經網絡初始參數進行離線優化，比較兩種算法在優化過程中適應度曲線的下降情況，再將優化所得初始參數帶入控制器中，與基本PID控制器在階躍信號輸入的條件下進行比較。使用階躍信號進行實驗加載，通過實驗驗證算法在實際上中的可行性。

4.1 仿真結果

仿真中所用模糊神經網絡為5層“雙輸入三輸出”，每層的神經元個數為2，18，81，81，3，相關參數分別為： 神經網絡的學習速率η=0.2，動量因子α=0.02，網絡權重ωij∈[-1， 1]，隸屬度函數寬度bij∈[-40， 40]，隸屬度函數中間值cij∈[-96， 96]。神經網絡學習迭代次數為500。SAPSO中群體個數m=300，空間維數n=243，加速度因子c1，c2均為2.05，SAPSO算法的迭代次數為300，退火常數λ=0.9，粒子的移動速度vmax=0.5，vmin=-0.5。使用Matlab進行仿真，PSO算法與SAPSO算法優化過程中的適應度曲線如圖6所示。

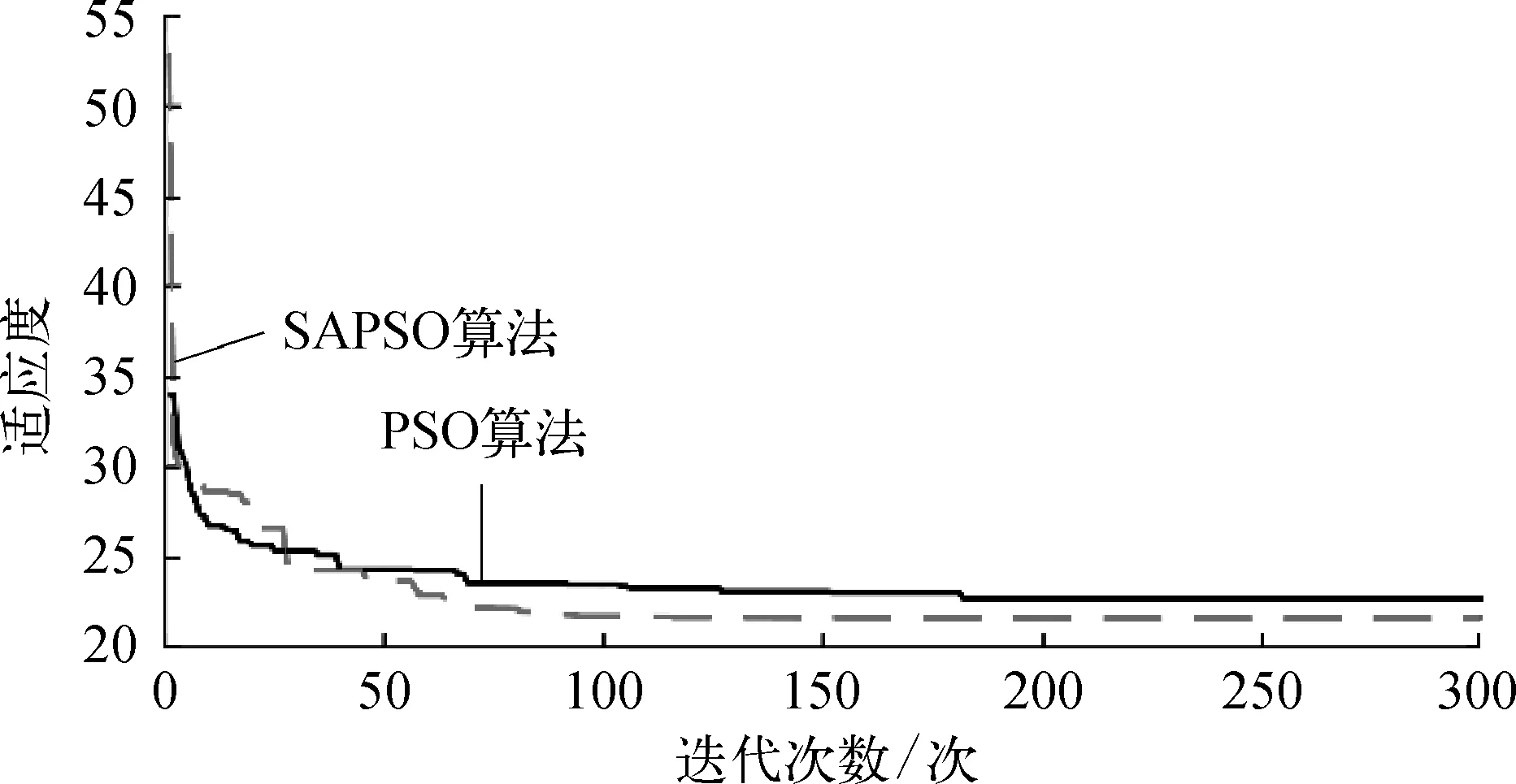
圖6 尋優過程示意

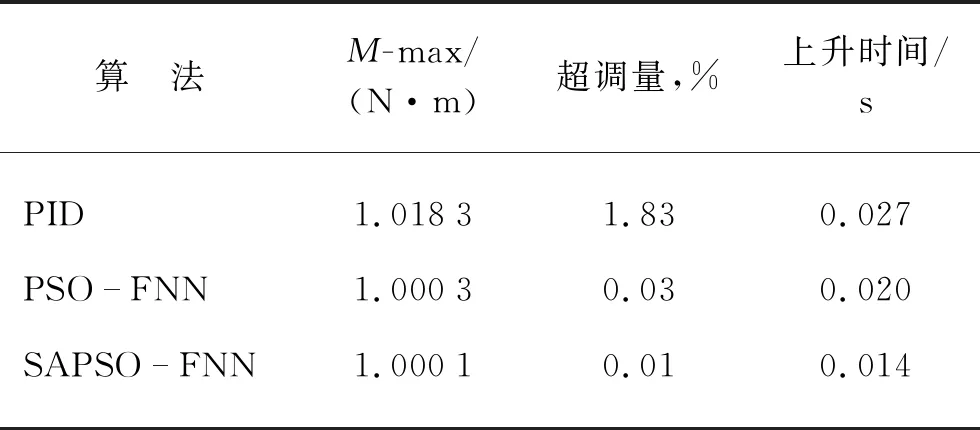
由圖6可以看出，由于SAPSO算法會在一定概率上接收較差的值，導致在適應度值下降速度方面，SAPSO算法稍慢于PSO算法，但同時由于SAPSO算法具有較強的跳出局部最優解的能力，使得SAPSO算法所求最優解的精度高于PSO算法，改善了PSO算法本身的不足，更好地跳出局部最優解。將SAPSO與PSO兩種算法帶入模糊神經網絡PID控制器中，比較階躍輸入信號在各個算法下的響應，仿真結果如圖7所示，階躍響應仿真性能指標見表2所列。

由圖7與表2可以看出基本PID算法下的響應較差，上升時間最長，且存在超調量。相比于PSO-FNN，SAPSO-FNN算法響應速度更快，且超調量更小。

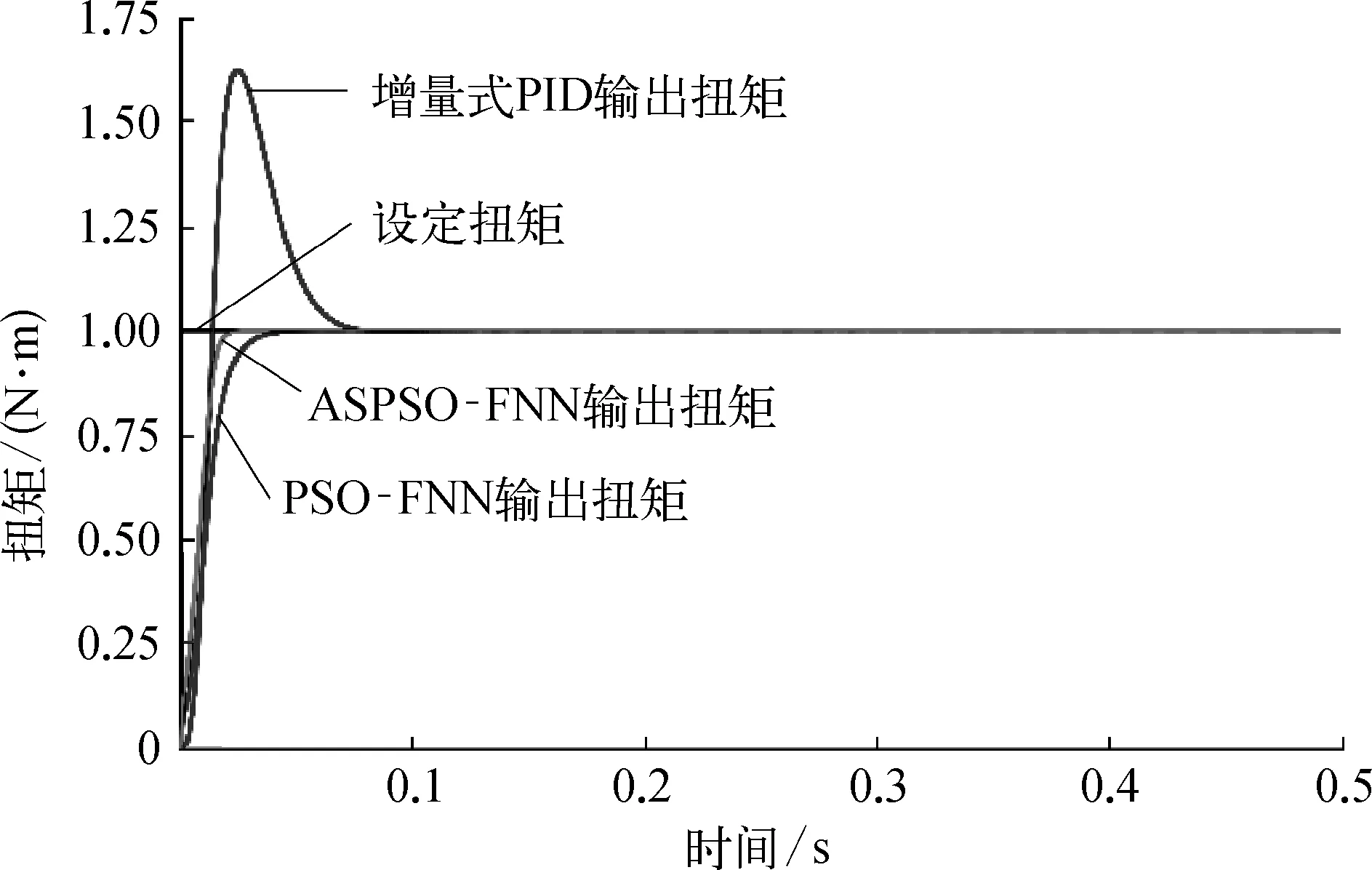
圖7 三種階躍響應仿真示意

算 法M-max/(N·m)超調量,%上升時間/sPID1.01831.830.027PSOFNN1.00030.030.020SAPSOFNN1.00010.010.014

4.2 實驗結果

使用TwinCAT3軟件中的ST語言進行編程，實現對加載電機的扭矩加載控制，輸入幅值為0.5 N·m的階躍信號，比較基本PID，PSO-FNN以及SAPSO-FNN的控制結果。其中PSO-FNN和SAPSO-FNN中的模糊神經網絡參數初始值采用上一部分仿真的優化結果如圖8所示，實驗中各個算階躍響應參數見表3所列。

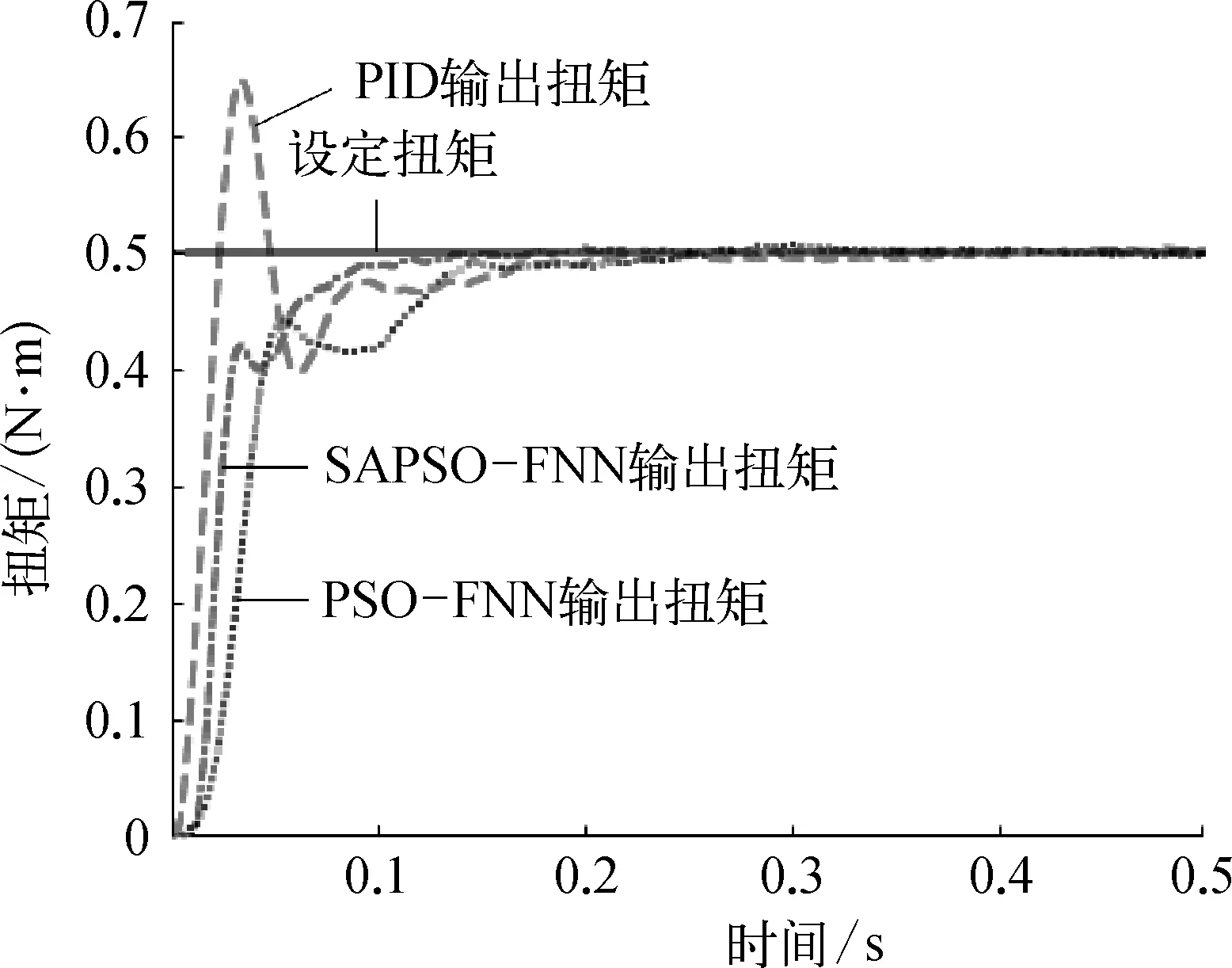
圖8 三種階躍響應優化結果示意

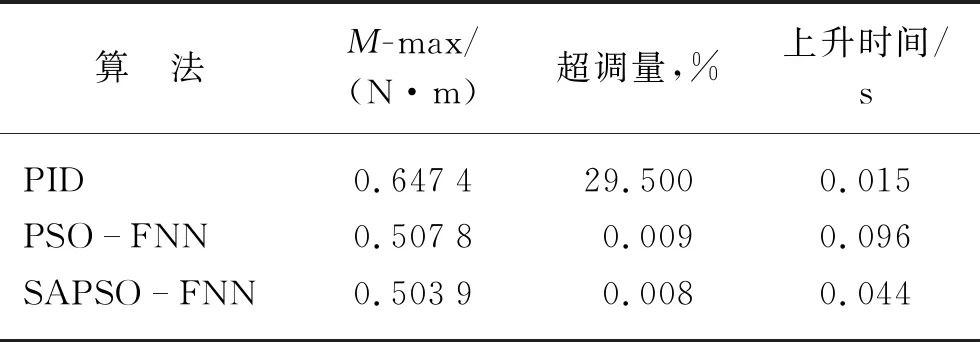
表3 階躍響應實驗性能指標

由圖8與表3可知，在控制加載電機的扭矩加載時，使用SAPSO-FNN的控制效果最佳，相比于基本PID，PSO-FNN，SAPSO-FNN算法具有調整時間短、上升時間短且超調量較小的優點，驗證了本文所設計的SAPSO-FNN控制算法的可行性。

5 結束語

1)電動式加載系統采用了減速器來增大輸出轉矩，引入了摩擦、間隙等非線性環節。基本PID控制器對于這些問題的控制效果較差，將模糊神經網絡與PID控制器相結合，產生的模糊神經網絡PID控制器對于該類問題的解決性較好。

2)模糊神經網絡PID控制器受初值影響較大，考慮使用基本粒子群算法進行參數優化易陷入局部最優，使用將模擬退火與粒子群算法相結合的基于模擬退火的粒子群算法進行參數優化。

3)使用Matlab軟件仿真，通過適應度函數的下降大小證明： 基于模擬退火的粒子群算法相比于基本粒子群算法在優化問題上具有跳出局部最優解的能力。

4)通過搭建蝸輪蝸桿試驗臺證明控制算法在實際中的可行性與SAPSO-FNN控制算法相比于PSO-FNN的優越性。