引入多級擾動的混合型粒子群優化算法*

徐利鋒, 黃祖勝, 楊中柱, 丁維龍

(浙江工業大學 計算機科學與技術學院,浙江 杭州 310023)

粒子群優化算法(particle swarm optimization,簡稱PSO)是由Kennedy和Eberhart于1995年提出的一種模擬鳥群覓食特性的進化算法[1].在算法中,粒子代表著覓食中的鳥個體.在每個粒子移動時,同時考慮整個群體的最優位置和當前粒子曾經經歷過的最優位置,類似于鳥群覓食時鳥之間的信息交流.當群體中所有粒子都移動之后,記為一輪優化迭代完成,接著進行下一輪優化迭代,直到滿足預設的迭代深度或者其他條件為止.整個群體就像鳥群覓食一樣,總是向著最優位置移動.

PSO算法具有易操作和收斂快等優點,但也存在著一些問題,比如因其收斂快而導致的易陷入局部最優值,以及算法在多局部峰值場景中的精確性不高等問題.研究者們一直在針對 PSO的這些問題進行針對性的研究和改進,并提出一些解決方法,形成了若干PSO的改進算法.其中,Shi和Eberhart于1998年提出的帶有慣性權重的粒子群優化算法[2],便是針對最初的PSO算法易陷入局部最優值的改進.Clerc于1999年提出了帶壓縮因子的粒子群優化算法[3],意在擺脫局部最優值的同時提高收斂速度.這是兩種最經典的改進PSO算法,其他的改進算法一般都是在此基礎之上通過與其他方法結合或是針對參數進行修改來獲得新的改進算法.例如,劉麗玨等人提出了基于克隆選擇的粒子群優化算法[4],主要利用了克隆和變異操作來提高算法的收斂速度,并保持種群多樣性.再如,針對多目標優化問題而提出的基于網格排序的多目標粒子群優化算法[5]、為逼近非凸或不連續的Pareto最優前端而提出的基于Pareto熵的多目標粒子群優化算法[6]、面向粒子群優化算法中學習因子自調節優化器的PSO算法[7]、基于粒子群優化算法的類集成測試序列確定方法[8]、加入了微生物行為機制的粒子群優化算法[9]以及微分進化算法與粒子群優化的結合[10]和其他一些針對 PSO參數進行自適應選擇的算法[11,12]等.這些改進的算法直接針對PSO算法本身存在的缺陷進行彌補.另外,還有一些改進算法實現了在不同領域中的適配和應用.對于算法適配,例如：對典型的NP難題中的Web服務組合優化問題,研究者提出了基于改進粒子群算法的Web服務組合[13];ECT系統中如果忽略電容傳感器的敏感場(又叫軟場),會使傳統圖像重建方法精度下降,為了清除這個瓶頸,提出了基于雙粒子群協同優化的 ECT圖像重建算法[14];為了在不修改源代碼的同時能夠評價優化目標的每個分支,提出了粒子群優化測試用例生成方法[15].對于算法應用,例如跳躍-滑翔軌跡優化研究(混沌粒子群算法)[16]、電力系統環保經濟負荷分配應用研究(空間粒子群優化算法)[17]以及求解服務鏈映射問題(離散粒子群優化算法)[18]等.

上述各種基于PSO的改進和適配后優化算法各有優點,但總體來說都是嘗試去解決原始PSO算法的固有問題——易于陷入局部極值的問題.針對這種問題,本研究基于現有的兩種經典改進PSO算法,在不過分提高算法時間復雜度的前提下,通過引入多級擾動策略來避免PSO算法易陷入局部最優值的問題,同時也能運用不同的擾動來處理算法探索能力差或算法提前收斂的情況.研究中,運用了 Sphere,Ackley,Rastrigin,Styblinski-Tang,Duadric和Rosenbrock函數對算法的性能進行了測試,并對不同的PSO相關優化算法結果進行對比驗證.本研究提出的改進型 PSO算法巧妙地結合了兩種經典的改進粒子群優化算法(帶慣性權重和帶收縮因子的粒子群優化算法)的特性,使得本算法能夠將這兩種優化算法的優點實現最大化的發揮.同時,針對易陷入局部最優這個問題,提出了多級擾動機制.總體來說,本算法不僅能夠增加粒子對于解空間的探索能力,還能夠較好地跳出局部最優值.本文首先在第1節介紹上述兩種經典的改進粒子群優化算法.然后,在第2節詳細講述了提出的新的改進型PSO算法,即混合型粒子群優化算法的概念及流程.在第3節中,通過對4個測試函數的結合應用,對混合型粒子群優化算法的可行性及準確性進行對比和驗證.最后,對本算法和相關的粒子群優化算法進行討論,對后續研究進行展望.

1 傳統粒子群優化算法

1.1 粒子群優化算法

最初提出的粒子群優化算法在模擬鳥群覓食的過程中,各個粒子的位置信息代表解空間中的一個可能的解,速度信息則代表粒子的更新(移動)動力.初始的粒子群優化算法總是能高效地進行更新,從而體現出收斂快的特點.

假設：所要優化的問題的種群大小為n,解空間維數為m,種群中每個粒子的位置為Xi(i=1,2,…,n),每個粒子的適應度值為f(Xi)(i=1,2,…,n),第k代中第i個粒子的位置為Xik,粒子的速度為Vik,第i個粒子得到的最優適應度值的位置為Pik(i=1,2,…,n),所有粒子中得到最優適應度值的位置為Pgk.公式(1)和公式(2)為粒子群優化算法中對于第k代粒子的速度、位置更新公式：

其中,c1和c2為學習因子,r1和r2為使速度具有隨機性的隨機數,取值在[0,1]之間.

從公式(1)和公式(2)中可以看出,粒子速度更新公式包含了3部分[19,20]：第1部分為粒子當前速度對于之前速度及方向的繼承能力;第2部分為粒子的自我認知部分,用來繼承粒子歷史屬性;第3部分為粒子的社會認知部分,表示為所有粒子之間的信息共享,合作地去探索更好的位置.但是由于此方法易陷入局部最優值,所以針對上述更新公式進行一定修改后,得到了下文所提到的兩種主流的改進算法.

1.2 標準粒子群優化算法

標準粒子群優化算法(standard particle swarm optimization,簡稱SPSO),即帶有慣性權重的PSO算法,在繼承粒子歷史速度時,引入慣性權重參數.目的是在尋優問題中,能夠先進行全局搜索,在縮小的搜索范圍或經過一段時間的搜索之后,再針對當前局部進行更為細致的搜索來獲得最優解.當慣性權重ω取值較大時,全局搜索能力強;較小時,局部搜索能力強.所以,該算法的慣性權重通常是線性遞減的[2].

假設：所要優化問題的種群大小為n,解空間維數為m,種群中每個粒子的位置為Xi(i=1,2,…,n),每個粒子的適應度值為f(Xi)(i=1,2,…,n),第k代中第i個粒子的位置為Xik,粒子的速度為Vik,第i個粒子得到的最優適應度值的位置為Pik(i=1,2,…,n),所有粒子中得到最優適應度值的位置為Pgk.公式(3)、公式(4)為標準粒子群優化算法中對于第k代粒子的速度、位置更新公式：

其中,ω為慣性權重,一般為線性遞減,運算方法見公式(5).

也有研究者使用一種基于對數遞減的慣性權重運算方式[21],見公式(6),一般取值由0.9遞減到0.4[22]：

其中,ωs為起始慣性權重值,ωe為結束慣性權重值,Tc為當前迭代深度,Tm為最大迭代深度.

除此之外,還有許多其他有關慣性權重的修改方法.例如指數遞減策略[23]、自適應慣性權重[24]等,在此不做詳細介紹.

SPSO算法的大致思路為：粒子群中每個粒子都有自己的位置及速度,每次迭代就相當于更新了群體中每個粒子的位置和速度,粒子的速度更新與粒子前一次速度及自身歷史最優位置和群體歷史最優位置與當前自身位置的差值有關,粒子的位置更新與速度有關.而 SPSO算法的特點是對于粒子的繼承能力部分,添加了一個慣性權重,以此來改變粒子歷史速度屬性對于當前屬性的影響能力.其主要思想為：在優化算法剛開始時,通過較大的慣性權重來使得粒子群的全局搜索能力強于局部搜索能力,而在算法不斷進行迭代優化之后,通過減少慣性權重來逐步加強粒子群的局部搜索能力.

1.3 帶收縮因子的粒子群優化算法

帶收縮因子的粒子群優化算法(standard particle swarm optimization with a constriction factor,簡稱PSOCF)流程與最初的PSO算法相似,區別在于粒子的速度更新公式不同.PSOCF運用收縮因子來對每次更新后的速度進行壓縮,從而提升收斂速度.

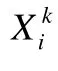
其中,φ為收縮因子.

與 SPSO算法不同,該算法的收縮因子不僅僅是改變了自身歷史速度的影響能力,同時也改變了歷史最優位置對粒子速度的影響能力.由于收縮因子是固定常量,為了能夠較好地平衡全局搜索與局部搜索之間的權重,一般使用公式(9)來計算收縮因子常量[3]：

PSOCF算法的特點是對于粒子的繼承能力、自我認知能力及社會認知能力部分,添加了一個壓縮因子,因此與SPSO算法相比,PSOCF算法在速度更新方面會更快地趨于穩定.其主要思想為擴大了慣性權重的影響范圍,因此PSOCF算法全局搜索能力的減弱速度以及局部搜索能力的增強速度都得到了提升,從而提升了整體算法的收斂速度.

2 新的帶多級擾動的混合型粒子群優化算法

SPSO和PSOCF這兩種改進優化算法各有特點.在粒子群算法中,不同的參數影響著算法不同的方面：慣性權重影響的是算法中粒子屬性的繼承性;而壓縮因子不僅影響繼承性,更影響了整體算法的收斂性.壓縮因子過大,收斂性差,且算法接近于隨機搜索優化;壓縮因子過小,則易提早收斂,導致結果可能為局部最優值,精度下降.從針對粒子進行分層[24]得到靈感,本研究提出的新型改進算法——帶多級擾動的混合型粒子群優化算法(mixed particle swarm optimization with multistage disturbances,簡稱MPSO),是將以上兩種優化算法的優點進行整合,在考慮粒子能夠較好繼承自身最優解和群體最優解的基礎上,引入多級擾動來增加粒子位置變異的隨機性以及防止粒子的早熟收斂.

粒子群優化算法具有收斂快的特點,使得算法容易陷入局部最優值而使得最終優化結果產生誤差,因此在本研究中引入多級擾動來防止早熟收斂.多級擾動策略分為兩級：一級擾動的主要作用是使粒子能夠更充分地遍歷解空間,類似于混沌擾動[25],都是為了增加粒子的遍歷能力;二級擾動則是為應對在多峰值情況下易陷入局部最優值的問題而提出的輔助策略,提高搜索結果的精度,類似于蜜蜂尋找蜂蜜.目前已尋找到暫時最佳的,但是仍需要再去其他地方探索觀察是否有更為豐富的蜂蜜,那么便假設此時刻的最優位置的食物已耗盡,以此為基礎再去尋找其他食物[26].一級擾動在粒子更新位置之后引入.具體的引入概率與當前迭代深度(Tc)及最大迭代深度(Tm)有關,見公式(10).

其中,ε為引入一級擾動的概率.得到的概率會隨著迭代深度的增加而減少.與此方法類似的是將粒子分為兩種：一種負責標準運行,另一種負責群體多樣性.將兩種粒子進行結合,可以趨近粒子在探索和收斂間的平衡[27].二級擾動在一級擾動判斷之后引入.是否引入二級擾動,與粒子是否早熟的判斷有關：若在優化過程探索期中最優粒子連續出現10次相同狀態(前期實驗表明：觸發二級擾動的相同次數分別為10,20,30,40時,精度都沒有顯著差異(見表1),因此設置為10次),則判定為局部收斂(早熟),從而引入二級擾動,使粒子快速跳脫出局部最優值.

MPSO算法主要是將優化過程的中前期定義為探索期,盡量保持較強的全局搜索能力;而在優化后期,為了快速收斂,盡量加強局部搜索能力.結合前述兩種經典優化算法的優點：探索期中利用慣性權重及一級擾動A(后文公式(12))在優化前期較強的全局搜索能力,盡可能的去遍歷解空間,并使用二級擾動來擺脫局部極值;在優化后期,則使用收縮因子及一級擾動B(后文公式(13))來增強粒子的局部搜索能力,從而完成收斂.

Table 1 Result of four optimization algorithms for different second disturb condition of five test functions表1 4種優化算法對于不同二級擾動條件的5種測試函數的優化結果

基于與前述現有算法相同的假設,MPSO算法具體優化流程如下.

Step 1. 初始化粒子群中所有粒子的位置和速度.

Step 2. 計算每個粒子的適應度值.

Step 3. 對于每個粒子,將此次優化得到的適應度值與其自身經歷過的歷史最優適應度值Pik進行比較,若優于Pik則更新該粒子的歷史最優位置.

Step 4. 當所有粒子都更新粒子歷史最優速度Pik之后,將每個粒子的適應度值與整個群體的最優值Pgk進行比較,若優于Pgk的適應度值,則對Pgk進行更新.

Step 5. 根據當前迭代深度判斷使用公式(3)、公式(4)還是公式(7)、公式(8)對所有粒子更新速度及位置.

Step 6. 更新適應度值.

Step 7. 根據公式(10)判斷是否引入一級擾動：若引入擾動,則到Step 8;若不引入,則到Step 9.

Step 8. 引入一級擾動后再次更新適應度值：若新適應度值優于原適應度值,則保留擾動;否則刪除擾動.

Step 9. 判斷當前收斂狀況是否滿足提早收斂的條件：

? 若滿足,則引入二級擾動,并回到Step 5;

? 若不滿足,則判斷是否滿足終止條件：若滿足,則結束算法;若不滿足,則回到Step 3.

第5步中的速度、位置更新算法有兩個：首先使用的是標準粒子群優化算法的公式(3)、公式(4),之后再使用帶收縮因子的公式(7)、公式(8).之所以選擇這種更新方式,是因為這兩種公式各有特點.例如,SPSO對解空間的探索好,而 PSOCF的收斂速度快.所以定義中前期為探索期,中后期則可根據情況實現收斂.將其兩者結合在一起,可使優化過程盡量徹底且全面,同時又能及時得到收斂得到優化結果.MPSO算法流程如圖1所示.其中的一級擾動的算法流程如圖2所示.

探索期時間點的定義,主要由通過一系列的前期預備實驗確定.要確定切換時間點,主要考慮算法的兩個因素：探索范圍的大小及探索最終結果的精度.由于探索范圍與迭代深度正相關,因此將探索最終結果的精度作為首要評價標準,在結果精度無顯著差異的情況下,將探索范圍的大小納入評判依據.

最佳切換時間的獲取也是一個優化問題,因此,將算法中的切換時間點作為優化目標,通過使用本文提出的混合型粒子群優化算法來獲取最優解.由于獲取最佳切換時間的算法執行中還會涉及探索期切換的最佳切換時間設置,因而為簡化起見,將最佳切換時間優化過程中的當次迭代深度的探索期切換時間設置為前次迭代探索到的最優解.本研究運用Sphere函數、Ackley函數、Rastrigin函數、Styblinski-Tang函數、Duadric函數和Rosenbrock函數進行仿真實驗,因此也對這6個測試函數的優化來獲取最優的探索期切換區間.

對這個子問題的優化過程的具體設置是：把切換時間點所處的算法總體迭代過程歸一化為[0,1]區間(將區間歸一化是因為在不同優化問題中,得到的范圍是不確定的,精度也是不確定的,因此為了拓展算法的通用性,將整體區間進行歸一化處理);設定優化算法中粒子個數為 10,粒子維度(探索步長)為 10;時間點探索迭代深度為100;函數極值探索的迭代深度為2 000;以對不同函數探索到的極值精度(或偏差度)作為適應度函數,評價比較切換時間點優劣.優化結果顯示,對所有函數來說,最優值(即極值)探索到的時間點基本上都在10/20～12/20之間(即迭代深度1000～1200).具體對比結果見表2.

Table 2 Optimization algorithm for the same dimension of the six test functions for the time switching point表2 優化算法對于相同維度的6種測試函數的時間切換點優化結果表

考慮算法存在的系統誤差以及一定的隨機性因素,將算法的切換時間點定義到合適的范圍區間.從表 2的結果,確定該區間范圍為[1/2,3/5].

本文提出算法的迭代深度到達切換時間區間后,通過判斷當前最優值第 1次出現的迭代深度來確定本次優化探索期結束的時間點.因此,本研究提出了公式(11),使得能夠方便地在歸一化后的區間找到時間切換點T：

其中,Tf為當前最優值第1次出現的迭代深度,Rsa為歸一化整體迭代過程中切換時間區間的開始,Rst為切換時間區間的結束.

為了針對不同狀態和特點的粒子,算法中所引入的一級擾動分為兩種不同的形式,記為A和B(如圖2所示).

· 一級擾動A在優化前期引入,主要作用是增大粒子對本身鄰域的探索能力;同時,reset保證了粒子有突破當前局限的可能性;

·B部分在算法后期引入,主要作用是對粒子位置進行小幅度的探索修正.

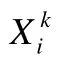
其中,r0為[-2,2]之間的隨機數,有關r0的取值將在本文下文中進行驗證;T為通過公式(11)獲得的時間切換點;r1,r2,r3為[0,1]的隨機數;ga為標準高斯隨機數(μ=0,σ=1,在[-3,3]的概率為99.8%);reset表示對當前粒子的位置在當前解空間中進行隨機重置.一級擾動A和B中是兩種不同的擾動方式,在具體實施中選擇其一進行,且兩者選擇概率是相同的.每次引入一級擾動之后,都要檢測當前引入的一級擾動是否使得適應度值更優：若更優,則保留此次一級擾動;否則,刪除當次擾動(避免無用擾動對結果產生影響).

算法中對粒子陷入局部最優的判斷：如果粒子連續10次的狀態都相同,那么便定義當前粒子陷入了局部最優值.若已陷入局部最優值,則會引入二次擾動.二級擾動主要是將粒子的位置重置為與當前局部最優結果有關的位置(見公式(14)),并且讓其脫離當前局部最優.但脫離結果不能過于隨機,因此運用了基于最優位置值附近的隨機位置分布,來更新粒子位置,從而達到脫離的效果：

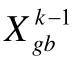
前述公式中,包含兩個隨機數r0和ra.這兩個參數在整個算法中,目的是增強粒子的探索能力和跳脫出局部最優值的能力,因此其取值對優化算法的改進比較關鍵.在本研究中,運用了一些前期預備實驗對這兩個隨機數的取值范圍進行探索.實驗中,首先設置了一個前提假設：這兩個隨機數的取值范圍是基于 0對稱的;隨后,選擇不同的上下限范圍,并對研究中涉及的測試函數(Sphere函數、Ackley函數、Rastrigin函數、Styblinski-Tang函數、Duadric函數和Rosenbrock函數)進行預運算;最后,對不同取值范圍下的優化結果進行評判.表2中列出了不同取值組合設置下的優化結果優劣比較——選用了[-2,2]范圍作為基準,將其他取值范圍的優化結果與[-2,2]的優化結果作對比.

· 若優化結果比基準要好,則認為該取值范圍更優;否則,記為更差;

· 在極值為0的測試函數優化中,若收斂精度差值不超過1,或者在極值非0的測試函數仿真中收斂誤差不超過1,則記為無差異;

· 基準本身不進行自身對比.

另外,在對不同的參數范圍進行比較時,我們將最優值為0的函數占最終結果的比重為0.5,最優值不為0的函數占最終結果的比重為0.5.由此,從表3中可以得出結論：當r0,ra取值[-2,2]時,對于最優值為0以及非0的情況的綜合效果最好.

本研究中所引入的多級擾動機制,實質是在相對穩定的優化過程中加入隨機性和變異性,并且針對于仍未跳出局部最優值的情況,提供了二級擾動,把粒子進行大幅度的移動,從而擺脫當前局部最優值的影響.若二級擾動引入后仍陷于局部最優值,則再次引入二級擾動….以此遞進,最多可進行64次(前期實驗表明,重復引入二級擾動的次數在16,32,64,128這4種設置下,除Sphere函數外,其余的函數都不能體現出顯著差異.而Sphere函數則是在64次重復引入的情況下,優化結果精度最高(見表4),因此,這里設置為64次).這是為了能在陷入無限循環之后,從其中跳脫出來的同時又能嘗試引入多次擾動來擺脫局部最優.

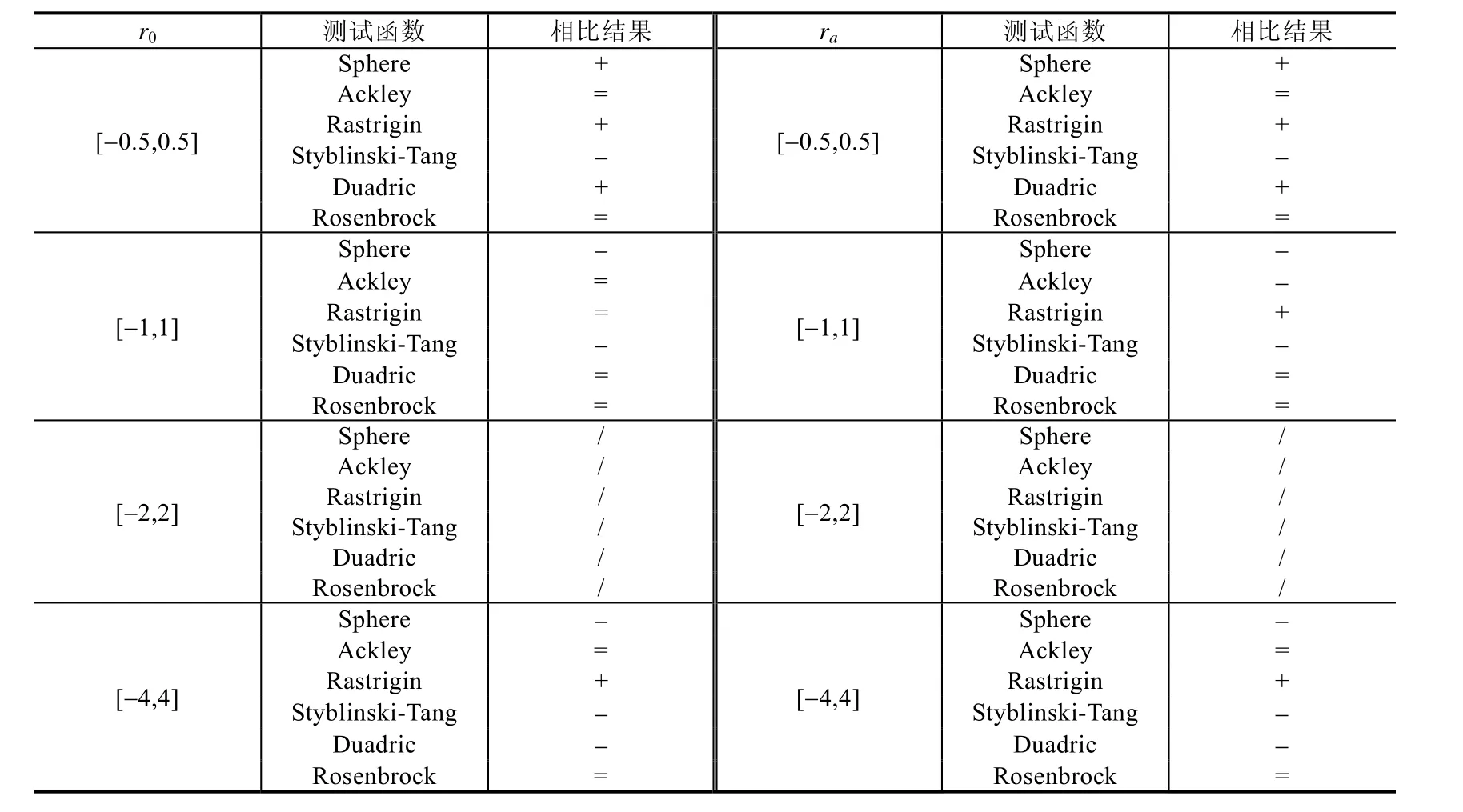
Table 3 Result of different r0 & ra to optimization algorithms for different dimension of sixtest functions表3 不同r0 & ra的MPSO算法對于對于不同維度的6種測試函數的優化結果表

Table 4 Result of four optimization algorithms for different max number of second disturb of five test functions表4 4種優化算法對于二級擾動不同最高次數的5種測試函數的優化結果表

本研究使用了異步粒子群優化算法的粒子更新方式[28].同步粒子群優化算法的粒子更新方式是在一輪粒子全部更新得到適應度值之后,再更新粒子最優及群體最優.而這種異步的形式是在搜索中,當任意一個粒子發現其計算的適應值優于共享信息中的適應值時,則立即更新共享信息,以此提高粒子的利用效率.同時,粒子群算法根據鄰域內粒子數量的不同,可以分為全局和局部兩個形式[1]：全局版本就是所有粒子都是其中某一顆粒子的鄰域成員,局部版本就是只有一部分粒子是某一顆粒子的鄰域成員.對于簡單的問題,鄰域內的粒子越多,效果越好;對于復雜的多模問題,鄰域內的粒子越少,效果越好[29],除此之外,還要一些其他的定義方式,如 4類結構、金字塔結構[28]、可變多簇結構[30]等.MPSO采用的是異步全局粒子群算法的形式.

在對指定優化問題進行優化時,粒子的運動范圍往往都是限定的,因此需要對超出限定閾值的粒子進行處理,處理方法一般有吸收墻、反射墻、衰減墻和隱匿墻[31].本研究運用了重置的方法——將超出閾值的粒子重置在閾值邊界附近,此方法近似于反射墻,但是反射能力被大大削弱,可稱為弱反射墻.假設當前問題限制的粒子閾值范圍為[-α,α],那么結合反射墻及衰減墻,可將弱反射墻的運算定義為如公式(15)所示形式：

其中,r4為[0,1]之間的隨機數.

算法整體的時間復雜度由原本的O(n)變為O(cn),其中,c為一個常數(c＞1),取值與引入擾動的次數呈正相關;n與粒子維度d、種群粒子數m、最大迭代次數t有關.

3 算法仿真實驗

在本研究中,為了測試MPSO算法的有效性,選擇了6個函數——Sphere函數、Ackley函數、Rastrigin函數、Styblinski-Tang函數、Duadric函數及Rosenbrock函數來進行測試.同時,運用現有的3個改進PSO算法——SPSO,PSOCF和 PSO-DT[32]進行相同條件的優化運算,再將三者的優化過程與結果進行對比與驗證.仿真實驗在Windows 10平臺中Eclipse環境中進行,硬件配置為Inter i5-2430M,RAM 4GB.

3.1 測試函數

1. Sphere函數.

函數在xi=0時達到全局最小值0,為單峰值函數.函數表達式見公式(16).

2. Ackley函數.

函數在xi=0時達到全局最小值0,且函數在解空間中存在大量局部極小值點.函數表達式見公式(17).

3. Rastrigin函數.

函數在xi=0時達到全局最小值 0,且函數在解空間中存在大量的正弦凸起的局部極小值點.函數形式見公式(18).

4. Styblinski-Tang函數.

函數在xi=-2.903534時達到全局最小值-39.16599乘上d(d為維度,表示自變量x的坐標數目),且為多維多峰多局部最優值函數.函數表達式見公式(19).

5. Duadric函數.

函數在xi=0時達到全局最小值 0,為單峰值多極值函數.此函數與 Sphere函數類似,但是考慮了維度因素d(此處同樣為自變量x的坐標數目),因此更容易陷入局部極值.函數表達式見公式(20).

6. Rosenbrock函數.

函數在xi=0時達到全局最小值0,為單峰值凹槽型函數.此函數在極值附近的值存在極微小的差別：

在標準粒子群優化算法中,有關參數的設置通常是類似的.一般來說,學習因子c1,c2取值范圍為[0,2],在算法中一般取值為2.0,而ω則是從0.9遞減到0.4[21],見公式(22).

而在帶收縮因子的實驗中,發現了當c=c1+c2=4.1,根據公式(7),得到φ=0.729時,PSOCF算法能夠較好的平衡探索及收斂能力[3].

因此,在本研究的仿真實驗中,設置各個算法的粒子規模n為5,10,15和20;標準粒子群算法中,c1=c2=2;慣性權重ω采用對數遞減,從0.9對數遞減到0.4;帶收縮因子的粒子群算法中,收縮因子φ=0.729,學習因子c1=c2=2.05.

3.2 仿真實驗結果與分析

通過仿真實驗,對上述4個函數進行優化測試：定義函數的全局極值為最優值;運用3種基于粒子群的優化算法(混合粒子群優化算法、標準粒子群優化算法以及帶收縮因子的粒子群優化算法)進行優化運算;算法中,設置4種步長維度(5,10,15和20,表示優化算法中粒子個數)分別進行運算;單次優化的終止條件為迭代次數達到2 000次;實驗重復次數為10次,取平均值對不同設置和場景(函數)分別進行比較.前3個函數——Sphere函數、Ackley函數和 Rastrigin函數因其全局最小值都為零,因此優化算法的優化效果以其最終優化結果值的精度表示,具體對比結果見表5.而Styblinski-Tang的全局最小值不為0,因此優化結果以算法優化值與函數極值之間的偏差來表示.偏差φ的計算方法由公式(23)計算而來：

其中,Vt為Styblinski-Tang函數的結果真值,op為優化算法得到的結果值.具體的結果對比見表6.

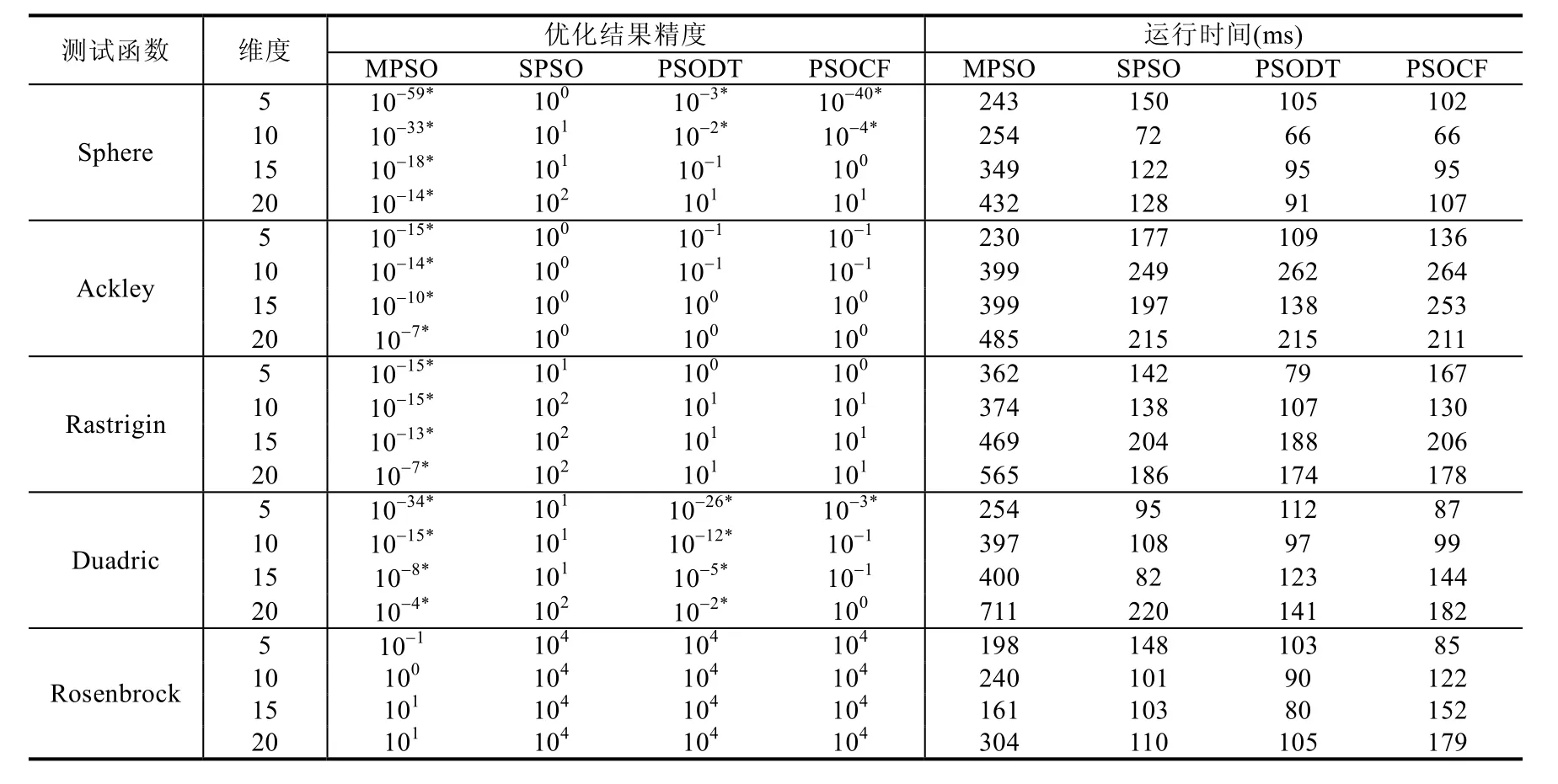
Table 5 Result of four optimization algorithms for different dimension of five test functions表5 4種優化算法對于不同維度類型的5種測試函數的優化結果表

Table 6 Result of three optimization algorithms for different dimension of Styblinski-Tang test functions表6 3種優化算法對于不同維度的Styblinski-Tang測試函數的優化結果表

從表5可以看出,在優化結果精度方面,在所有的4種不同維度設置下,本研究提出的MPSO算法對3種最優值為 0的測試函數的優化結果都顯著優于另外兩種改進算法的結果;并且在其他算法無法定位到最優值的情況下,MPSO算法依然能夠找到最優值,且具有較高的精度.具體來說,在Sphere和Ackley函數上,PSOCF算法也能找到正確的最優值,但是在最后結果的精度上與MPSO算法仍有較大差距;對Rastrigin函數的優化結果來說,PSOCF不能找到正確的最優值,而MPSO的最終結果精度較高;而SPSO算法對這3個測試函數的優化結果的精度都處于最低的位置,幾乎都未能定位到最優值.

從維度上來說,隨著測試函數維度的提升,所有算法的優化結果精度都相應降低.從表5中可以看出,在實驗中設置的維度范圍內,本研究提出的MPSO都能準確的找到最優值并保證一定的精度;SPSO算法在此范圍內基本上都沒有能夠找到最優值;PSOCF算法則是在對Sphere函數和Ackley函數的的優化中,以5和10為維度時能夠找到最優值并進行一定的精度探索;但在15和20維度,則并不能夠找到最優值.

整體優化迭代過程如圖3～圖8所示.結合圖3～圖6可以發現,在優化前期(探索期),MPSO算法一直在探索,直到后半期轉入低幾率弱一級擾動B后開始逐漸收斂,而在切換更新公式后進行了快速收斂;而 SPSO算法則較為穩定,一直在探索,最終并沒有很好地收斂在最優值上;PSOCF算法則是在一開始就在最優值附近開始快速收斂;PSODT與PSOCF算法類似,但是最終優化結果的精度在5維度、10維度時沒有PSOCF算法精確.同時能夠發現,其他3種算法在5維度、10維度的Sphere函數優化時效果較好;在5維度、10維度的Ackley函數優化時效果一般,但還是找到了最優值,但在一定深度之后則趨于穩定,不再繼續探索;而在其他情況下則并沒有找到最優值,而是在局部最優值附近進行快速收斂.從圖中我們可以清楚地發現MPSO算法的特點：在探索期中,以探索為主;在后半優化過程中,以快速收斂為主.這樣就能較好地在平衡探索與收斂基礎之上,優化到最優值.而從圖7能夠發現：無論哪種優化算法在維度超過5時,得到的優化結果都不夠精確;但對同樣的優化問題而言,本研究提出的混合型粒子群優化算法總是能得到精度更高的優化結果.

從時間上來說,本研究提出的MPSO算法中,耗時的主要是引入的多級擾動.因為每次引入一級擾動之后都要重新計算一次適應度值,并因為早熟而引入二級擾動后,重新去引入一級擾動,所以整體時間為原本的2倍～4倍.多出的時間主要為計算適應度值情況下,對原本算法的整體算法流程上所耗費的時間并沒有增加,只是增加了一些引入擾動后重新計算適應度值的時間.

從表6可以看出,對最優值不為0的Styblinski-Tang函數的優化測試中,當維度分別為5和10時,MPSO算法的精確度較好;但當維度為15和20時,偏差接近3%.在考慮到真值較大的情況下,這種偏差率可以接受;SPSO算法在維度為5和10時,偏差度達到了3%左右.雖然偏差度有些大,但還在可接受范圍;但是在維度為15時,偏差超過了9%;而在維度為20時,偏差更是達到了16%,這表示了偏差過大,優化結果不夠準確;而PSOCF算法在測試的維度為 5,10,15中的偏差都超過了 10%,在維度為 20時更是超過了 20%,說明 PSOCF算法對于Styblinski-Tang函數優化能力很差;PSODT算法相對于SPSO和PSOCF算法來說要更為優秀,但其優化精度仍然不如MPSO算法高.結合圖8同樣也發現,MPSO在前半優化過程中以探索為主,在后半優化過程中以快速收斂為主.這樣就能較好地在平衡探索與收斂基礎之上,優化到最優值.這也體現了MPSO算法在上述情況下的優化結果都優于其他兩種算法,同時,耗費時間大概為其他兩種算法的2倍～4倍.

4 結 論

針對經典粒子群優化算法易陷入局部最優及收斂速度較慢等問題,本研究在分析經典的兩種粒子群優化算法SPSO和PSOCF的基礎上,提出了帶多級擾動的混合型粒子群優化算法.原始的粒子群優化算法在多局部極值情況下容易陷入局部最優值.SPSO和 PSOCF算法正式針對這一特點而進行了改進.本研究中提出的MPSO算法結合了這兩種經典改進優化算法的優點,引入多級擾動的策略,利用多級擾動干擾粒子探索進程,使粒子在本身速度和位置更新之外,獲得了一種“震動”,不但增長了算法對局部極值附近的探索能力,也擴展了算法在陷入局部最優值時的跳脫能力,從而在保證算法及時收斂的情況下,使粒子群優化算法的探索能力和最優值的精度上都得到極大的提升.

通常認為,在PSO相關的算法中最重要的參數是慣性權重和學習因子[33].如何選擇、調整這些參數,會直接影響粒子群優化算法的收斂性和結果的有效性.在本文中,粒子更新公式中的慣性權重使用的是對數遞減形式.另外,還有其他方法對慣性權重進行遞減用以針對不同的優化問題,而如何結合具體優化問題設置不同的慣性權重并加以應用、如何對其他參數進行適應性設置以及如何根據迭代情況自適應的去尋找最優參數,這些都沒能在本研究中進行實驗和探討.

本研究中對整個優化周期進行了簡單的定義——分為探索期和收斂期.在探索期內,粒子保持跳動能力,對整個解空間進行搜索;而過了探索期之后,則允許其進行收斂.這樣的分割對學習因子和慣性權重的應用起到了至關重要的作用.因此,研究中對兩個時期的切換時間點做了細致的前期實驗,而在后續的仿真實驗中,發現前期實驗所得的最佳切換時間點所處區間確實很好得平衡了搜索能力和收斂能力.另外,算法中運用的兩個隨機參數r0和ra,取值對整體算法的優化能力有比較關鍵的影響.本研究中,在基于經驗取值的基礎上,對著兩個參數的取值進行了不同設置下的對比和前期驗證.對于優化算法中的參數取值,總是在不同的應用場景下往往有不同的表現.例如,本文提出的MPSO算法在對間作中的不同作物的間作模式有較好的優化和預測作用,但其與對不同環境下的水稻田間種植模式優化過程的參數設置和適應度函數選取都有不同的策略.因此,很難說在普遍的場景下有一個通用的取值.在這種情況下,運用其他較為成熟和穩健算法先期對參數進行優化是一個比較好的選擇.另外,如果能開發出對不同場景自適應調整的智能策略,將能夠比較有力地推動優化問題解決及優化算法方面的研究.