基于GM(0,n)灰色預測模型的構造預測及定量評價

高 雅

(1. 中煤科工集團西安研究院有限公司，陜西省西安市，710054；2.陜西省煤礦水害防治技術重點實驗室，陜西省西安市，710077)

我國煤系地層復雜的構造條件是各類地質條件形成的主控因素，嚴重制約著我國煤炭的安全高效開采。近年來，不斷提高的煤礦生產機械化程度要求對井田的構造規律做出更加深入的研究。許多礦井地質構造條件復雜，且對礦井未采區域地質構造規律的認識模糊不清，導致采掘工作常常處于被動局面，直接制約著煤炭產量、威脅著生產安全。這就需要在采掘工程未開始前，能夠對未采區域的構造復雜程度做出一定的預判。受限于傳統的構造規律研究方法，急需從構造的預測及定量評價這一難題中尋求突破口。能否在采掘工程開始前，通過量化研究得出未采區采掘范圍內構造的發育規律，成為了煤礦實現生產安全以及提高經濟效益的關鍵。

從礦井構造預測概念的提出到目前判別分析法、構造指數法、等性塊段法、模糊綜合判斷法、灰色系統理論及人工神經網絡等多種定量化評價預測方法的應用，國內外學者在構造定量化研究方面做了大量工作。為了得到與實際礦井揭露基本一致的預測評價結果，基于對井田構造發育規律的充分分析，選取最優評價指標，結合灰色模糊綜合評價和灰色系統建模的方法對井田未采區域地質構造的復雜程度進行了量化研究和綜合評價。

1 井田概況

蘆嶺井田位于宿東向斜西南翼的東南段，含煤地層為石炭、二疊系，主采8#、9#、10#煤層。斜切斷層在井田內較為發育，走向以NNE、NE向為主，NW、NNW向次之，總體呈現為局部斷層密集，切割關系復雜，力學性質扭性為主；井田內的褶皺構造有：宿東、王格莊向斜及小史家背斜等，斷裂構造多分布于應力集中的褶皺軸部，且小斷層、小褶皺也分布較多。普遍發育的層滑構造對主采煤層造成大面積破壞，對生產造成了很大影響。

目前，該井田一水平已回采完畢，二水平正在開采，三水平處于準備階段，針對井田未采掘區域開展構造預測及地質構造復雜程度定量評價，不僅給未采區在采掘規劃的形成和開采方式的選取上提供了理論依據，也對礦井的可持續發展、安全高效開采意義重大。

2 定量評價指標的確定

作為定量評價地質構造復雜程度的基礎，評價指標的確定直接關系到評價結果的準確性。鑒于不同區域不同井田多樣化的構造條件以及開采方式、生產機械化程度的差異，統一的指標體系套用是不可取的，必須與礦井實際情況緊密結合。在此基礎上，才能合理地確定礦井定量評價的指標。

井田內構造以斷裂構造為主，由于已采區的范圍較廣，地質勘探及采掘揭露數據較多，可較易獲取各類構造復雜程度定量化研究所需的經濟、技術指標；而對于未采區，勘探工作尚未全面開展，部分評價指標不容易獲取。因此，結合礦井地質構造特征和生產的需要，本文選取全礦井評價指標和已采區評價指標兩類指標。

2.1 全礦井評價指標

(1)褶皺復雜型指數(W)。它反映褶皺的緊密程度和煤層傾角大小的變化關系。

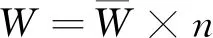
(1)

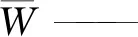
n——統計單元內等高線條數，條。

(2)斷裂分維值(K)。它是反映斷裂構造復雜程度的一種準確有效的指標。本次采用計盒維數法，在煤層底板等高線圖上分別劃分了250 m×250 m、125 m×125 m及62.5 m×62.5 m的網格，通過計算得到斷裂分維值。

(3)煤層底板傾角變異系數(R)。它反映統計單元內煤層傾角的變化程度。

(2)

ai——第i個統計單元的煤層傾角，(°)；

n——統計單元數。

2.2 已采區評價指標

(1)斷層密度(M)。它反映一定范圍內斷層的發育程度。

(3)

式中：k——斷層數，條；

S——統計單元面積，104m2。

(2)斷層強度(F)。它反映斷裂構造的發育程度。

(4)

式中：li——第i斷層的水平延伸長度，m；

hi——第i斷層的水平延伸長度和落差，m。

(3)斷層走向影響指數(Q)。它反映不同走向斷層對生產的影響。

(5)

式中：θi——斷層與煤層的走向夾角，(°)；

Li——斷層水平延伸長度，m；

n——斷層條數，條。

(4)褶皺平面變形系數(P)。它反映褶皺構造復雜程度。

(6)

式中：h0——相鄰兩條等高線的標高差，m；

L0——計算單元中心兩條等高線間的水平距離，m；

L1——靠近計算單元中心的等高線在單元內的實際長度，m；

L2——靠近計算單元中心的等高線在單元內的割線長度，m。

3 定量評價標準

結合井田構造特點，依據《礦井水文地質規程》中地質構造4類劃分法，得到井田已采區各評價指標的復雜程度分類標準(表1)。依據表1構造復雜程度分類標準，構建了井田已采區地質構造復雜程度定量評價模型，劃分了簡單、中等、復雜和極復雜4類構造等級，評價結果基本符合礦井實際揭露情況，證實了評價結果的合理性，可以作為未采區構造復雜程度定量評價的標準。

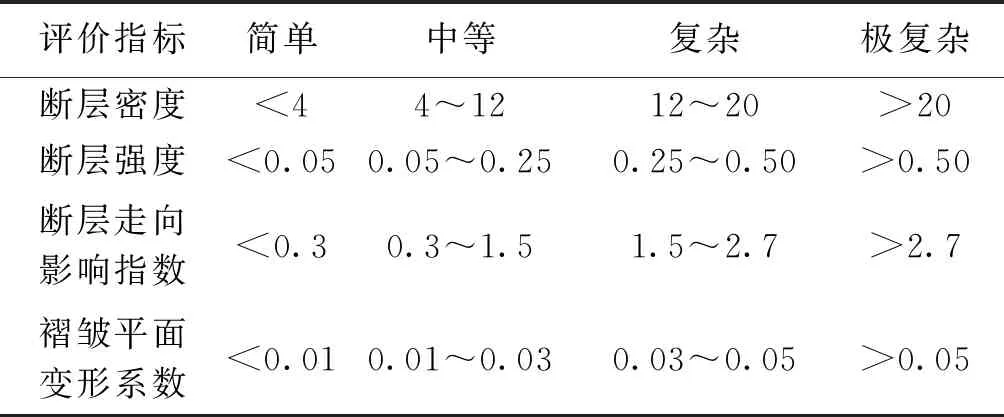
表1 井田已采區各評價指標的復雜程度分類標準

4 未采區構造預測

4.1 定量預測模型的建立

灰色預測模型種類較多，有多種可用于本次模型的建立。基于對井田內定量化評價指標可選擇度以及可選擇指標大數據真實度上的綜合考慮，本次選擇GM(0,n)模型，即用零階微分方程建立n個變量的靜態數學模型來建立定量預測模型。

(1)數學模型。GM(0,n)數學模型：

(7)

式中：a、bi——待定系數，其中，i=1,2，……，n-1；

xi(1)——第i個變量的原始數據累加處理后的取值。

記原始數據序列為：

一次累加處理后的數據序列為：

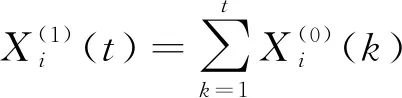
記：

由最小二乘法可求得：

(8)

將式(2)計算結果代入式(1)，得到GM(0,n)模型。

(2)預測模型。首先，對已采區內的7個評價指標，即斷層密度、斷層強度、斷層走向影響指數、褶皺平面變形系數、褶皺復雜性指數、斷裂分維值及煤層底板傾角變異系數進行了統計分析，繼而運用GM(0,n)灰色預測模型建立了各評價指標的GM(0,4)構造預測模型：

①斷層密度(M)：M=-0.8209×W+12.6460×K+16.4047×R-11.2466

(9)

②斷層強度(F)：F=-0.001×W+0.0654×K-0.0169×R+0.0565

(10)

③斷層走向影響指數(Q)：Q=-0.0712×W+1.6589×K+3.1076×R-0.0028

(11)

④褶皺平面變形系數(D)：D=0.0002×W+0.0147×K-0.0250×R+0.0107

(12)

4.2 預測模型檢驗

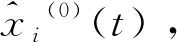
據表2可知，本次建立的GM(0,4)灰色預測模型相對誤差都在5%之內，預測精度較好，可以用于未采區的地質構造預測。

4.3 未采區構造定量評價

依據上面建立的GM(0,4)構造預測模型，以未采區10#煤層底板等高線為底圖，在圖上選取平行和垂直煤層總體走向的網格線來繪制正方形網格單元，累計劃分500 m×500 m網格19個，并對每個網格單元內褶皺復雜性指數、斷裂分維值及煤層底板傾角變異系數的值進行統計，然后通過GM(0,4)構造預測模型得到斷層密度、斷層強度、斷層走向影響指數和褶皺平面變形系數的參數值，如表3所示。

繼而借助灰色模糊綜合評價方法，采用因素權重和評價指標程度權重相結合的雙權重，并根據井田已采區構造復雜程度定量評價標準，求出未采區地質構造復雜程度評價系數的計算結果，見表4。根據最大隸屬度原則，完成了井田未采區地質構造復雜程度的定量評價，如圖1所示，劃分了構造簡單、構造中等、構造復雜和構造極復雜4類構造等級，并明確了各構造等級的分布狀況。

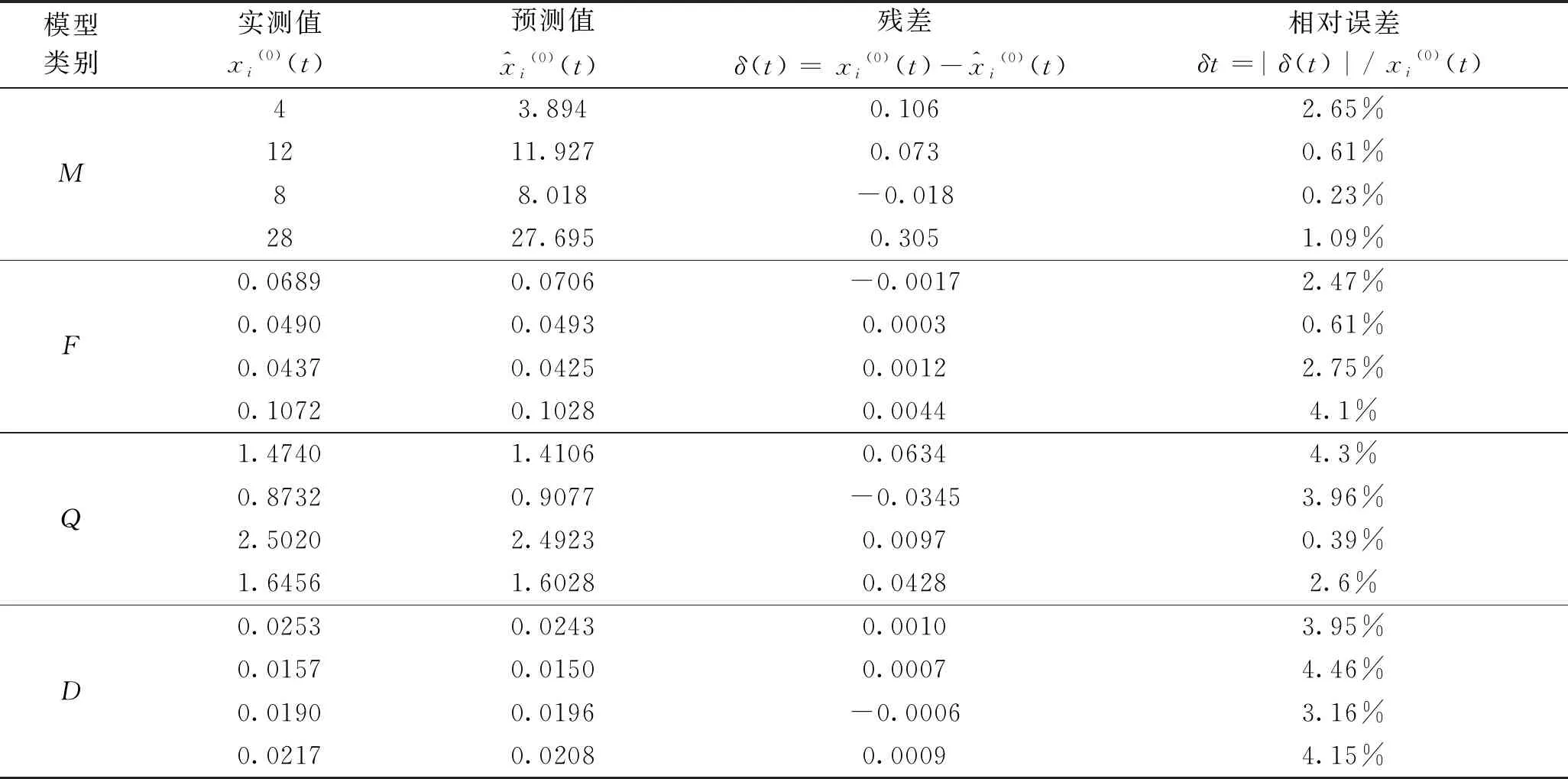
表2 井田已采區評價指標誤差檢驗表

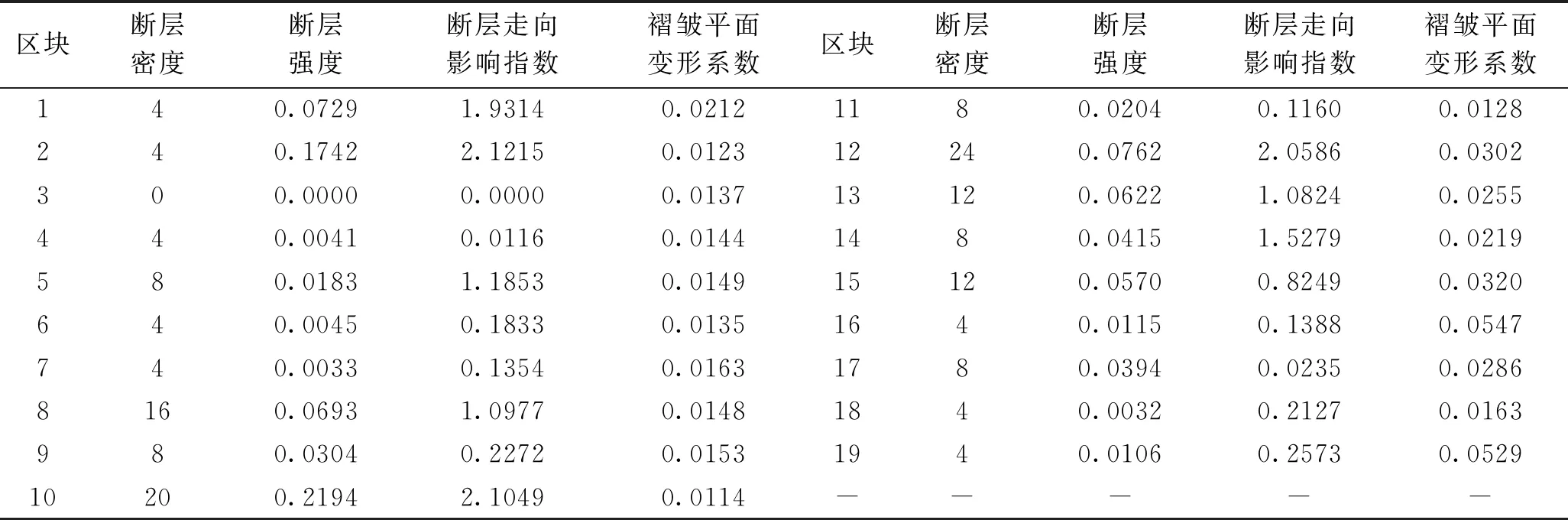
表3 未采區各網格單元評價指標預測值

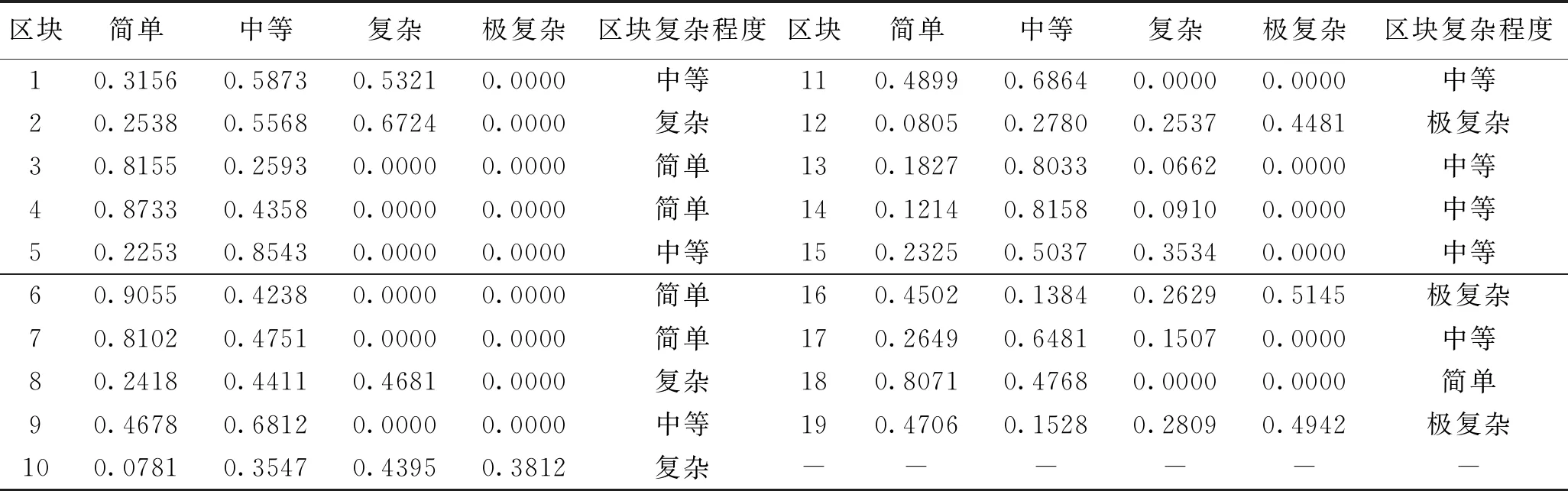
表4 未采區地質構造復雜程度評價系數計算結果

據圖1可知，井田大部分未采區域內構造等級中等，構造簡單區域主要分布在西部和東部邊緣部分，構造復雜和構造極復雜區域分布在未采區的南部和北部，總體上，井田未采區的構造復雜程度屬于構造復雜型。

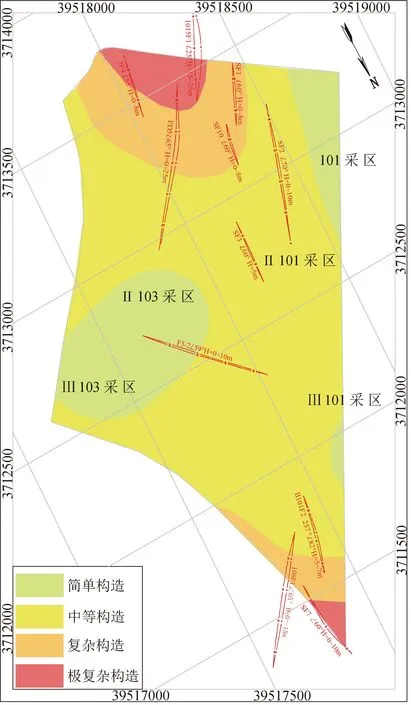
圖1 未采區構造復雜程度定量評價結果圖

5 結論

本文通過灰色模糊綜合評價及灰色建模預測，建立起井田未采區地質構造的定量預測模型，對未采區各評價指標的參數值進行了預測，并依據建立的井田已采區地質構造復雜程度定量評價標準，對未采區地質構造復雜程度做出了定量評價，得到如下結論。

(1)基于對已采區內篩選的7個評價指標參數值的統計分析，借助灰色建模預測方法建立了未采區GM(0,4)灰色構造預測模型，并驗證了預測模型預測精度的可靠性，證明了本預測模型可以用于未采區的地質構造預測。

(2)通過建立的未采區地質構造預測模型求得了未采區各評價指標的預測值，并利用建立的已采區地質構造復雜程度定量評價標準完成了未采區構造預測及定量評價，得出在該井田未采區范圍內構造簡單有5個單元，構造中等有8個單元，構造復雜和構造極復雜各有3個單元。未采區構造中等及中等以上區塊占到全區的74%左右，未采區的構造復雜程度總體上屬于構造復雜型。

(3)由于該井田未采區實際揭露資料較少，還需進一步探討和研究構造預測精度等難題，使得到的構造預測結果最大限度地接近地質實際。