融合鄰域魯棒性及度均衡性的集體影響中心性

宋甲秀，楊曉翠，張曦煌

(江南大學物聯網工程學院，江蘇 無錫 214122)

0 引言

受益于評估節點影響力標準的多樣性，節點影響力度量方法的研究也是各有側重。本文，主要關注復雜網絡中基于網絡結構中心性指標的一類影響力度量方法。這類方法又可分為基于網絡全局結構、基于網絡局部結構、基于特征向量中心性的影響力度量方法等。一般地，局部度量指標效率較高，但是度量效果不盡理想，如度數中心性、局部中心性等。而以接近度中心性、介數中心性為代表的全局度量指標雖然更為有效，但計算復雜度普遍很高。相比之下，k-核中心性在時間復雜度上有極大改善，但由于粗粒度特性的存在，使得其無法區分部分節點的影響力大小。特征向量中心性指標及其變體方法更適用于有向網絡，在無向網絡上效果不佳。近來，Flaviano Morone和Makse[1]在Nature上提出了一種復雜度較低的基于滲流理論的集體影響(Collective Influence，簡稱CI)中心性指標。關于其有效性，在文獻[1]～[3]中均有所證明。直觀地來看，該指標考慮了節點的度數和l層所有鄰居的度數(l可取1,2,3…)，但忽略了節點鄰域可能存在的不平衡結構以及鄰域間連接緊密程度的差異，導致其在異質性明顯的實際復雜網絡適用中，表現出很大的局限性。對此，本章創新性地提出了基于鄰域平衡性及魯棒性的節點影響力度量方法NewCI(New Collective Influence)中心性，并通過實驗結果證明了該方法能夠在保留原CI中心性較低計算復雜度優勢的同時突破其局限性，有效性得到進一步地增強。

1 相關工作

在信息傳播過程中，位于網絡特殊位置的某些節點往往能夠引發大規模的信息擴散[4-5]。較之于其他節點，此類節點在影響力方面具有明顯優勢，以產品的病毒營銷、流行病傳播等場景中最為常見。這些影響力節點的識別對于理解和分析網絡中的各類信息流動過程有著重要的作用，與如今形式多樣的生活應用更是密切相關。近年來，學術界對于節點影響力度量方面的研究也是在不斷突破，取得了相對豐富的成果。其中，給定復雜網絡中節點位置的結構信息，衡量單個節點影響力最簡單的方式是基于中心性的啟發式度量，如度中心性、k-核、介數和PageRank等。這些指標主要是根據網絡中單個節點在擴散過程中的作用大小進行排序，并以此作為對節點影響力的衡量，為后續實現加速或限制信息擴散的目標提供理論支持。

直觀地，擁有大量連接的節點應該具有更大的影響力，這也是度中心性指標的核心思想。關于此理論的合理性，于無標度網絡脆弱性的早期研究中[6]有所揭示。該研究認為節點的連接數對動態過程的影響是非線性相關的，針對網絡極少數的高度節點進行攻擊，會使得服從重尾分布網絡中的巨大連通圖迅速崩潰。此外，與其他較復雜的中心性指標相比，度數的計算復雜性可以忽略不計，所以度中心性被視為識別影響力節點最簡易有效的方法之一。

然而，度中心性存在一明顯不足，表現為該指標只考慮了節點的一階鄰居數量，忽略了節點所處位置的網絡信息。大量實證表明多數的傳播現象是以層疊的方式進行的。因此，單個節點影響力的最終評估也應該受到全局網絡結構的作用。此外，在實際的復雜網絡中，高度節點在網絡的核心位置以及邊緣部分均有出現的可能。這也就意味著以度作為影響力節點識別指標，在真實世界中并不可靠。據此，Kitsak等人通過對各種實際社交網絡上的數據在SIS和SIR模型上進行了廣泛的模擬證實了這一推測[7]。取決于節點在全網絡中位置的差異，兩個度數相等的節點在SIR模型的傳播過程中可能會感染完全不同的人群。相較而言，k-核指標可以區分網絡的核心位置和邊緣部分，且能在O(m)(m為網絡邊數)的運算時間內完成分解過程，故被廣泛應用于大規模復雜網絡分析。一般認為，具有低k-核指標值的節點被大量的低度鄰居包圍，會限制影響的傳播，而位于核心區域的節點(高k-核指標值者)可以通過其高度鄰居促進大規模擴散。但在SIS模型下，由于I群體被治愈后仍然可能被再次感染，所以高k-核區域一直會存在I群體。對此，文獻[8][9][10]考慮到網絡中高k-核區域的局部結構信息，提出了幾種更為一般化的強化k-核方法。

除了k-核指標之外，特征向量中心性也可作為基于全局網絡結構的指標。該指標認為節點的影響力取決于其鄰居的傳播能力。首先給網絡中的所有節點分配統一的聲望分數，聲望分數一般初始化為向量(1,1,…,1)T∈Rn(n為網絡節點數)，該分數會沿著邊進行傳播直到達到穩定狀態為止。在計算過程中，聲望分數傳播的每一個迭代對應于當前得分向量左乘網絡的鄰接矩陣。該過程實際上是通過冪迭代來計算鄰接矩陣的主特征向量及其對應的特征值，聲望分數向量最終會收斂到最大特征值的右特征向量。PageRank和LeaderRank算法都為基于特征向量中心性的著名變體。

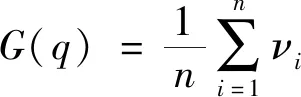
無獨有偶，Flaviano Morone等人[1]為解決影響最大化問題，把尋找一組最小化的種子節點對網絡中信息擴散進行控制使其達到免疫狀態這一問題，精確地映射到最優滲流模型中，并提出CI中心性來對量化個體節點的影響力。該中心性度量方法考慮了節點間的拓撲相互作用，卻對節點鄰域分布以及網絡結構的健壯程度未予關注。基于此，本文在CI中心性的基礎上，對其所忽略的重要影響因素分別進行了分析、定義及量化，繼而創新性地提出了在一般化網絡下仍然普遍適用的影響力度量方法—NewCI中心性。通過在真實復雜網絡數據集上進行的節點免疫網絡抗毀性實驗，證明了該中心性影響力度量方法在性能上具有很高的穩定性，且對影響力大小度量的準確性優于CI中心性。

2 算法描述

2.1 定義描述

滲流理論：是復雜網絡理論研究中的一個重要發現，主要包括鍵滲流和點滲流。給定無向網絡G(V,E)，在鍵滲流的模型下，G中的每條邊以一定的概率q被保留，同時以1-q的概率被刪除。當q=0時，所有的邊都會被刪除；隨著q的增大，G中將會保留了較多的邊并形成一些網絡簇；僅當q大于臨界閾值qc時，G中會出現規模為O(|V|)(V為網絡節點集)的巨型連通分量。點滲流模型與鍵滲流模型類似，不同之處在于保留概率q被分配給節點而不是邊。

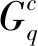
(1)

(2)

其中，向量v=(v1,v2,…,vn)表示節點是否屬于巨型連通分量，vi取值為1(或0)，表示節點vi屬于(或不屬于)該巨型連通分量。在刪除節點等量的情況下，G(q)的值越小，說明網絡分裂越嚴重，反映出所刪除節點在網絡中承擔的角色越重要，即個體影響力較大。

連通分量的數量：給定初始網絡G(V,E)，C(q)為基于某種特定的中心性度量方法刪除nq數目的節點之后的網絡中連通圖的數量，連通分量的數量分數Rc則定義為C(q)與初始網絡G的規模的比值，即

(3)

式中Rc的值越大，網絡的分段就越多。Rc(q)=1時，網絡將完全分散，所有的節點之間幾乎相互孤立，網絡的性質也就不復存在；Rc(q)=0時，則表示網絡為一個連通網絡，具有較強的抗毀性。在以刪除相同數量節點為前提條件下，C(q)和Rc(q)都可通過網絡被破壞的碎片化程度來衡量這些節點的實際影響力。

2.2 基本方法介紹

本文主要就五種最為常用的節點影響力度量方法進行簡要介紹，包括介數中心性[4,13-14]、接近度中心性[4,15]，k-核[16]、特征向量中心性[17]以及CI中心性[7]。它們也將作為后續實驗研究中的基準方法。

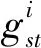
(4)

接近度中心性(Closeness Centrality，簡稱CC)[4]，定義連通網絡G中節點vi的接近度中心性為從該節點到所有其他節點的最短距離平均值的倒數，即

(5)

其中，dij為節點vi與節點vj間的最短距離。顯然，CC值越大，節點越處于網絡中心，影響力就越大。

k-核(簡稱k-core)方法[13]的主要思想基于核心度，即認為位于網絡核心部分的節點的影響力要高于邊緣節點。實現流程如下：設網絡的孤立節點的核心度為0，并將其從網絡中去除，而后進行k-核分解。首先，把所有核心度為1的節點從網絡中移除，之后繼續移除剩余度小于等于1的節點，直到網絡中所有剩余節點的剩余度都大于1為止。該步中所有移除的節點即為1-核節點，其核心度都等于1。接著遵循以上步驟，對網絡中核心度為2的節點進行處理。以此類推，直到網絡中所有的節點都被移除。在該方法下，較大核心度的節點意味著位于網絡更中心的位置，有更大的影響力。

特征向量中心性(Eigenvector Centrality，簡稱EC)[17]認為節點的影響力取決于鄰居的數量以及其影響力，定義節點vi的特征向量中心性如公式(6)，可通過冪迭代方法計算得出。

(6)

Α={aij}

(7)

其中，c為比例常數，一般取1/λ，λ為鄰接矩陣A的最大特征向量。

集體影響(Collective Influence，簡稱CI)[7]是一種中心性優化方法，旨在尋找在最優滲透模型下使網絡結構碎片化的最小影響力節點集，該指標從選擇節點并將其刪除給網絡中巨型連通分量所帶來的破環程度來衡量節點的影響力大小。定義Ball(i,l)為圍繞節點vi，且屬于半徑(最短路徑)為l的球內的節點集合，?Ball(i,l)為該球的邊界，那么節點vi的CI中心性值為

(8)

其中，ki是節點vi的度，l是預定義的不超過有限網絡的網絡直徑的非負整數，在大中型網絡一般取3，小網絡中取2。

2.3 融合鄰域魯棒性及度均衡性的集體影響中心性度量方法

真實的復雜網絡中普遍存在著異質性，如微博、Twitter等社交網絡，考慮該因素對提出合理的節點影響力度量方法有著重要意義。而CI中心性只考慮到了節點的度數和以該節點為中心，半徑在l(節點間的最短路徑)的球面邊界上所有節點的度數，忽略了由于優先連接造成的度分布不平衡問題所帶來的影響。

如圖1所示，首先，本文針對多個節點的CI中心性度量值相等的情況，對各節點所對應的局部拓撲結構進行詳細分析。簡單起見，1)令l=1，后續的分析將推廣至l階鄰居，2)以局部樹狀網絡為研究起點，逐步擴展到節點及其l階鄰居的局部聚類系數不為0的一般網絡。根據CI中心性的定義可知，CI中心性度量值相等的節點無外乎是兩種情況：一是其一階鄰居節點的數量相同，且一階鄰居節點的度之和也相等，如圖1a和c中的節點1。如此一來，一階鄰居的度分布平衡與否便成為了區分兩節點影響力的關鍵，本文稱此問題為目標節點的1階鄰域的度均衡性。第二種則是其一階鄰居的數量不相等，如圖1a和b中的節點1。

除了目標節點的一階鄰居節點度分布及其一階鄰居數量這兩個因素之外，目標節點的一階鄰居的鄰居之間的相互連接關系也會對該節點的影響力評估產生影響，本文稱此因素為1階鄰域簇間連接強度。鑒于在CI中心性度量方法中，半徑l考慮的是最短路徑，所以該因素并不會對CI的計算結果產生影響。以圖1e為例，節點一階鄰居的鄰居之間的連接關系對應于最外層球面節點的連接情況。顯然，節點6和節點7、節點12與節點13之間的連接在目標節點1從網絡中去除后，不會對碎片化網絡的連通分量的數量以及巨型連通分量的規模產生影響。然而節點7與節點9、節點10和節點12之間連接的存在與否，將導致在對目標節點進行相同的操作后，網絡結構會產生截然不同的變化。

此外，還有一個不容忽視的影響因素：目標節點一階鄰居間的連接關系，本文稱之為鄰域魯棒性，以局部聚類系數這一基本網絡特征來衡量。假設突破CI中心性度量方法對于局部樹狀網絡的限制，推廣到一般化網絡，節點局部的網絡拓撲結構將會發生巨大變化。如圖1d，若目標節點1在樹狀網絡中的一階鄰居全部沒有互相連接(即虛線鏈接不存在)，即該節點的局部聚類系數為0，其與一階鄰居的局部拓撲結構是樹狀網絡；隨著一階鄰居互連強度的增大，該節點的局部區域的結構趨于穩定，當該節點的聚類系數增加到1時，其與一階鄰居節點在拓撲上則構成了全連接網絡圖(圖1d中虛線鏈接全都存在的情況)。不難發現，目標節點在樹狀網絡中被刪除后，該網絡因抗毀性差，迅速分段瓦解成多個碎片網絡。而在全連接網絡中，網絡結構具有較強的健壯性，刪除目標節點后，網絡仍然連通。因此，網絡中目標節點的一階鄰居間連接關系的復雜性對于準確有效地衡量節點的影響力至關重要。

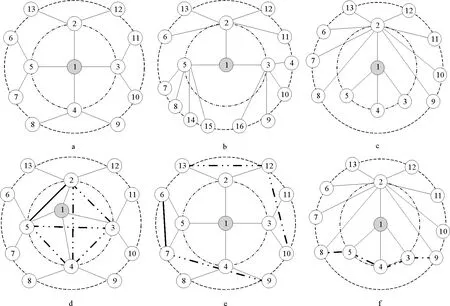
圖1 NewCI中心性分析示意圖Fig.1 Analysis diagram of NewCI centrality

綜上所述，CI方法忽視了研究目標節點的度數及其1階鄰域度均衡性、1階鄰域簇間連接強度、鄰域魯棒性等四個與影響力節點的度量相關的因素。本文對其進行改進，將1階鄰域度均衡性、1階鄰域簇間連接強度推廣到l階鄰域，對目標節點的l階鄰域度均衡性、l階鄰域簇間連接強度、鄰域魯棒性給出了相應的定義與分析，并以真實復雜網絡為應用背景，提出更具合理性的影響力度量方法。同時，針對目標節點的度數這一影響因素，制定出相應的排序局部調整策略。以下，將就這些概念逐一介紹。

2.3.1l階鄰域度均衡性

節點的l階鄰域度分布的異質程度是評估節點影響力的重要因素。為了量化l階鄰域節點度分布的均衡程度，本文定義l階鄰域度均衡性如式(9)。其中，Nl(i)表示節點vi的l階鄰域的節點集合，kj代表節點vj的度。分母中的第一項理解為l階鄰域度的振幅與l階鄰域度的理論中間值的比值，加1為防止分母為0的平滑操作。

(9)

目標節點的l階鄰域各節點的度越均衡，去除該節點后分裂成的網絡碎片，規模會相對更均衡，網絡中巨型連通分量會驟減，即該節點在網絡中的影響力更強。反之，則越弱。基于此，本文將CI中心性方法修正為NewCIB中心性(New Collective Influence centrality based on Neighborhood Balance)方法，如式(10)。當Bl(i)為1(目標節點的l階鄰域各節點的度絕對均衡)時，該方法退化為CI方法。

NewCIB(i)=Bl(i)CI(i)

(10)

為驗證NewCIB中心性方法的合理性，本文以圖1a,c舉例說明。令l=1，節點1為研究對象，根據式(8)兩圖中節點1的CI中心性值都為24。NewCIB(1)考慮了鄰域度分布均衡性，節點1對應的鄰域節點的度均衡程度越高，則NewCIB值越大。對于a，c兩圖中的目標節點1，根據式(10)計算出的NewCIB方法值分別為24、16.8，表明節點1的刪除對a網絡的破壞性更大，與圖中所反映的實際情況一致。由此可知，與CI中心性方法相比，NewCIB方法對節點影響力大小的評估更為準確。

2.3.2l階鄰域簇間連接強度

如上所述，在目標節點l階鄰域的節點度分布均衡性一定的情況下，l階鄰域節點間的連接情況則成為評估節點影響力的主要干擾因素。其中，目標節點的l階鄰域簇內節點間的連接(圖1e中的連邊(6,7)和(12,13))與該節點的刪除對網絡的破壞性相互獨立。而其l階鄰域簇間節點間的連接(圖1e,1f中的虛線)則影響了刪除該節點后的網絡連通性，增強了網絡的健壯性。更直接的表述是，虛線連接之后的網絡，目標節點的影響力減弱。本文中以目標節點的所有鄰居節點為簇頭的網絡簇中l階鄰域連通簇的數量來定義l階鄰域簇間連接強度這一影響因素。

對于目標節點vt，Nl(t)表示其l階鄰居的集合，l階鄰域連通簇對(Connected cluster pairs)的集合記為Ccp(初始化為?)，N(x)為vx的鄰居集合。當|Nl(t)|=1時，l階鄰域連通簇的數量為1。當|Nl(t)|>1時，對于任意vi，vj∈Nl(t)，且j>i，利用Ψij來判斷vt所有鄰居節點為簇頭的網絡簇之間在l階鄰域上是否連通，即

Ψij=(N(Nl(i))-N(Nl(i))INl(i))INl(j)

(11)

此時，若Ψij=?，表明以vi和vj為簇頭的網絡簇之間不連通；Ψij≠?，則連通，連通簇的簇頭對集合記為{(vi,vj)}。所以有

(12)

記Ccp中簇對所形成的連通簇團個數(Number of connected clusters)為Ncc，目標節點的鄰居中未和其他簇頭連通的節點數，即獨立簇頭個數(Number of independent cluster)為Nic，則最終目標節點的l階鄰域連通簇的數量為

Tc=Ncc+Nic

(13)

l階鄰域簇間連接強度定義為

(14)

同樣，CI中心性方法不能實現根據l階鄰域簇內節點間的連接存在與否以及連接強度對節點影響力的大小進行區分。為克服這一不足，在目標節點l階鄰域的節點度分布均衡性一定的情況下，本文將CI方法重寫為NewCIS中心性(New Collective Influence Centrality based on Neighborhood Strength Coefficient)方法：

NewCIs(i)=Sl(i)CI(i)

(15)

以圖1a和e、c和f為對比，來分析驗證NewCIS中心性方法的合理性。首先，當e和f中虛線不連接時，根據式(8)得到目標節點1在4個圖中的CI均為24。其次，虛線連接后，e和f中目標節點1的NewCIS分別為12和6。顯然，簇間連接的加入，會使得e(或f)中目標節點1的影響力弱于a(或c)，與實際情況相符。

2.3.3 鄰域魯棒性

為了量化節點的局部鄰域結構拓撲的健壯性差異對節點影響力大小的影響，本文引入“鄰域魯棒性”概念來衡量目標節點的鄰域節點間連接的密集程度，認為鄰域節點間的連接越密集，網絡結構的魯棒性則越強，反之亦然。這里采用目標節點的局部聚類系數這一網絡統計量來計算其鄰域魯棒性，形式化表示為

(16)

考慮到目標節點的鄰域魯棒性與其在網絡結構上發揮的影響力成反比，且該節點鄰域節點間的連接程度會直接影響鄰域節點的度分布均衡性，本文修正CI中心性方法為NewCIB/R中心性(New Collective Influence centrality based on Neighborhood Balance and Robustness)方法，定義如下：

(17)

接下來結合圖1a、d來驗證NewCIB/R中心性方法的合理性。在圖1a、d中，節點1為研究對象，即目標節點。a中節點1的CI中心性值為24；d中節點1的CI值會隨著其聚類系數的增加而增加，當節點2與節點5之間有連接時，目標節點的CI值為30。顯然，節點1在a網絡中被刪除之后，該網絡會分解成4個碎片網絡，而圖d中，由于節點2與節點5的相互連接，刪除節點1后，該網絡只分段為3個碎片網絡，且巨型連通分量更大，說明了節點1在a網絡中有更大的影響力，這與兩圖中由CI中心性方法所度量的影響力結果相悖。然而，基于本文的NewCIB/R中心性方法，節點1在a網絡中的NewCIB/R中心性值同樣為24，但在d圖中該節點的NewCIB/R中心性值為21.4，與CI中心性方法相比，NewCIB/R中心性方法對目標節點的影響力度量更為合理。

同上思路，基于節點的NewCIS中心性度量方法，其鄰域魯棒性也能加強度量方法的有效性，故在CI中心性指標的基礎上融合節點的l階鄰域簇間連接強度與鄰域魯棒性，定義NewCIS/R中心性(New Collective Influence Centrality based on Neighborhood Robustness and Strength Coefficient)方法為：

(18)

綜上所述，結合l階鄰域度均衡性、l階鄰域簇間連接強度、鄰域魯棒性等CI方法忽略的影響力度量影響因素，本文定義NewCI中心性方法為：

(19)

其中，參數α一般取0.5。

需要補充的一點是，NewCI中心性方法是針對目標節點的鄰居數目一定，CI值相同的情況(圖1a、c、d、e、f)而設計，并不能適用于鄰居數目不等，CI值相等的情況。如圖1a、b所示，兩圖中目標節點1的鄰居數分別為3和4，CI值均為24，且l階鄰域度均衡性、l階鄰域簇間連接強度以及鄰域魯棒性都相等，故二者的NewCI值相等。但b中節點1的影響力顯然比a中的要弱。也就是說，在這種情況下，目標節點本身的度是具有最高優先級的考慮因素。因此，本文制定排序局部調整策略如下：在對網絡各節點的影響力進行度量時，若出現多個節點NewCI相等的情況，將根據鄰居數目對這部分節點進行降序排列，以強化結果的整體合理性。注意，該策略只為實驗中確定影響力節點的相對排名而用，并不作為節點影響力度量方法。

2.4 時間復雜度分析

給定復雜網絡G=(V,E)，這里V和E={(u,v)|u,v∈V}分別表示網絡中的節點集和邊集，n和m依次代表V和E的規模。NewCI中心性影響力度量方法的計算復雜度主要由節點的CI中心性度量、l階鄰域度均衡性、l階鄰域簇間連接強度以及鄰域魯棒性等4部分計算復雜度組成。其中，節點CI的計算復雜度與該節點l階鄰域節點的數量有關。由于網絡中節點的平均度為〈k〉，則任意節點的l階鄰域的平均節點數量為〈k〉*〈k〉l-1，則計算網絡所有節點CI的復雜度為O(n*〈k〉*〈k〉l-1)。對于目標節點l階鄰域度均衡性和l階鄰域簇間連接強度的計算，復雜度均為O(〈k〉*〈k〉l-1)，節點的鄰域魯棒性的計算復雜度為O(1/2*〈k〉*(〈k〉-1))。所以，NewCI中心性影響力度量方法的最終時間復雜度為O(n*(3*〈k〉*〈k〉l-1+1/2*〈k〉*(〈k〉-1)))。又由于真實世界的復雜網絡通常是稀疏的，節點的數量n和邊數量m存在著m=O(n)的相關關系，所以〈k〉=2m/n可以記為一個常數，故算法的時間復雜度可近似為O(n*(3*〈k〉l+1/2*〈k〉2))，而l的取值一般較小。因此，NewCI中心性影響力度量方法具有較低的時間復雜度，符合基于網絡局部的中心性方法所具有的優勢。

3 實驗結果與分析

節點的影響力大小主要通過免疫該節點給網絡帶來的破壞程度來體現，本節即從該角度對NewCI中心性的性能進行實驗驗證。實驗中l的取值一般為2，與CC、BC、EC、k-core以及CI等5個代表性方法進行對比。

3.1 實驗環境與數據集介紹

實驗的硬件環境為Intel(R) Core(TM) i5-3210 CPU @ 2.50GHz，8 GB的內存。操作系統為window7。開發環境Visual Studio Code 1.15.1，開發語言為python 2.7。網絡分析工具包括snap-4.0.1版本、networkx-1.11版本、Gephi 0.8.1beta等。

為充分評估NewCI中心性的性能，本文選取了6個領域不同的真實復雜網絡數據集，包括：1)Celegans[18]：秀麗隱桿線蟲神經元網絡；2)Power[18]：美國西部電力網絡，以發電站或中轉站為節點，高壓傳輸線路為邊；3)Citeseer[19]：由科學出版物和引用鏈接組成的引文網絡；4)Literature_1976[20][21]：荷蘭文學評論數據集，節點為文學作者或評論家，邊表示評論家對文學作者工作的評價；5)Sawmill[21][22]：某企業內部員工的通信關系網絡；6)ModMath[21]：現代數學方法在美國賓夕法尼亞州Allegheny縣的小學和中學課程中的傳播網絡。網絡中的節點表示學校的主管領導，邊則表示管理者之間的友誼關系。

各數據集的基本網絡拓撲特征如表1，依次為節點數量(n)、網絡邊數(m)、平均度(〈k〉)、最大度(kmax)、網絡中節點的平均聚類系數(C)、節點間的平均最短路徑(〈d〉)、同配系數(r)、節點度分布的異質性(H)[23-24]以及傳播閾值[6,25](λc)。其中，H=〈d2〉/〈d〉2，λc=〈k〉/(〈k2〉-〈k〉)。

表1 實驗數據集的基本拓撲特征Tab.1 Basic topological features of the experimental datasets

3.2 節點免疫的網絡破壞性實驗

本節對最終的NewCI中心性方法在6個真實復雜網絡數據集上進行實驗和結果分析。其中，各真實網絡中G(q)、C(q)隨著q值變化的情況描述如圖2，各方法在6個實驗數據集中的執行效率記錄如表2。

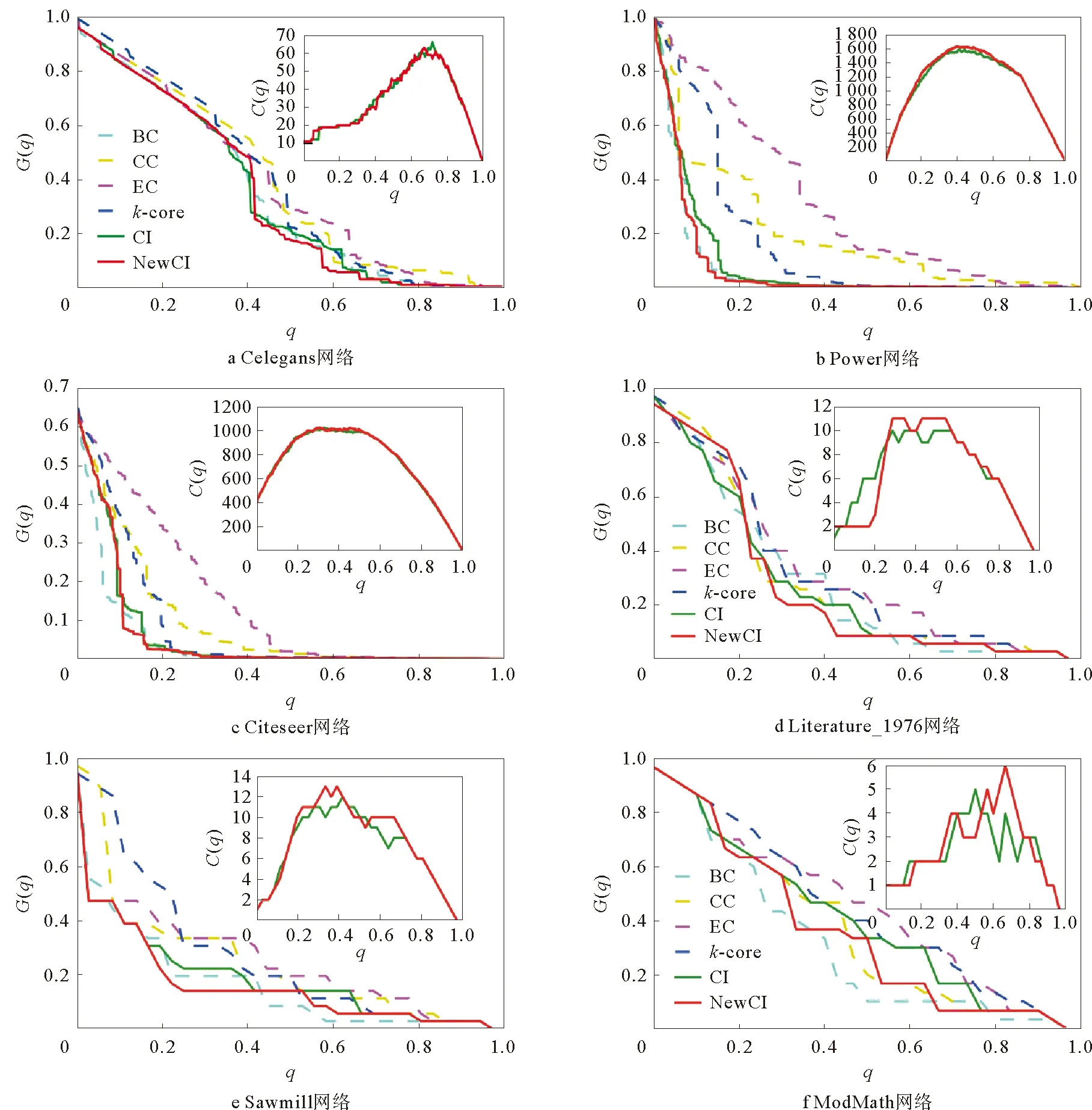
圖2 不同中心性方法在節點免疫的網絡破壞性實驗中的表現Fig.2 Performance of different centralities in network destructive experiments of node immunity

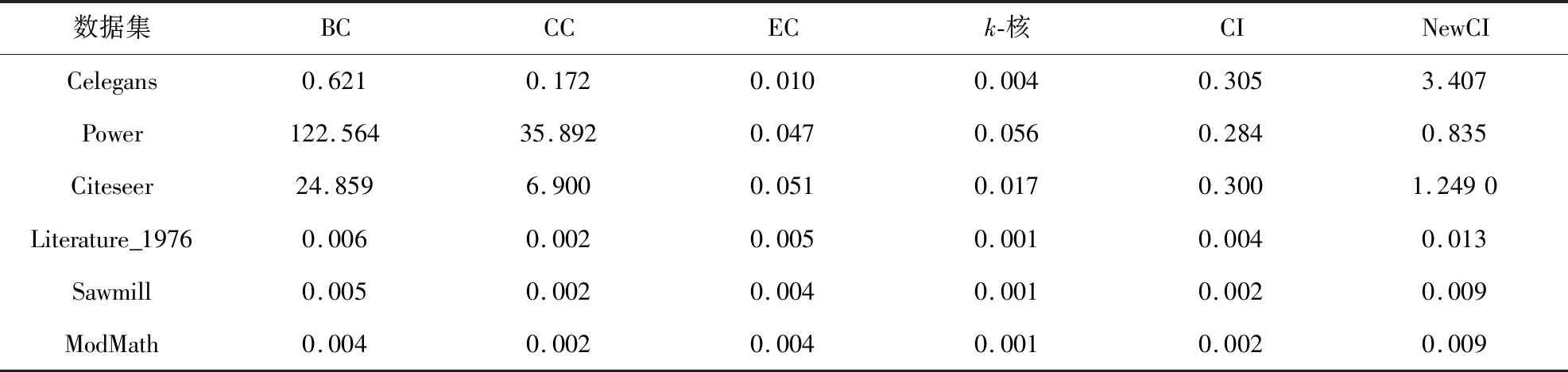
表2 各中心性方法在真實數據集中的執行效率Tab.2 Execution efficiency of each centrality in real datasets

顯然，NewCI中心性度量方法的表現穩定優于CI中心性方法。如在圖2a Celegans網絡中，NewCI中心性在q約等于0.576時，網絡中G(q)的規模從43直接減小為22。而CI中心性方法完成這一變化，即達到相同的網絡破壞程度，網絡中刪除節點的比例q須達到0.623，可見NewCI方法較CI提高了約7.5%的性能。在圖2b power網絡中，q為0.10時，NewCI中心性使該網絡中G(q)的規模從1 088個節點急劇減小為629。而CI中心性的最優分裂點在q=0.151處，此時網絡中G(q)的規模僅從856個節點減少到515個節點。同樣是使目標網絡中的G(q)的規模達到網絡規模的10%，NewCI的性能相比CI大約提升了34%。在其他的實驗數據集中的結論與此類似。

整體而言，在節點刪除的最初階段，G(q)隨著節點的刪除會劇烈減小，當超過一個最優的比例q之后，刪除節點對網絡的破壞作用減弱。而NewCI相比其他方法，曲線的下降趨勢更為快速。其中，該方法在Celegans、Power、Literature_1976以及Sawmill 4個網絡集中均為最佳；在Citeseer和ModMath中的表現也僅以微弱差距次于BC中心性方法；在所有數據集上都領先于CI，充分證明了其對節點影響力大小評估的有效性和準確性。與G(q)相對應，C(q)在最初階段隨著q的增加急劇增加，達到極值之后，呈現減小趨勢。在該指標之下，本文的NewCI中心性在Power、Literature_1976、Sawmill以及ModMath 4個網絡數據集上的表現同樣明顯優于CI中心性，在其他兩個數據集中，也能取得和CI相當的效果。

從表2各方法的執行效率來看，NewCI中心性的執行時間比與經典的BC、CC方法更短，與其他方法的執行時間同處一個數量級。

綜上所析，在所有中心性方法的對比中，以NewCI中心性方法與BC中心性方法的表現最好。NewCI中心性于各個類型的網絡中的表現均能穩定地優于CI中心性，肯定了該方法對CI中心性方法性能的提升，同時也驗證了其在度量節點影響力問題上的有效性，以及在應用網絡方面的普適性。較短的執行時間，使得其在較大規模的網絡中依然可行。

4 總結與展望

從節點免疫的網絡破壞性角度來看，NewCI中心性較CI中心性表現出更高的有效性和普適性，打破了CI中心性方法僅適用于樹狀網絡的局限。與各中心性方法相比，該方法與BC中心性方法展示出最佳的性能。綜合有效性、時間復雜度及執行效率三者考慮，NewCI中心性則優于其他中心性方法。

近年來，網絡表示學習技術興起，逐步成為解決大規模網絡數據網絡數據的有效手段。基于網絡表示學習技術實現對網絡中節點影響力更為準確和快速的評估，以適用于多關系網絡等新型網絡，將是本文下一步的研究任務。