基于抗震的油氣管道管溝設計方法研究

全 佳 李樞一 董江潔 邊文娟

1. 中國石油工程建設有限公司西南分公司, 四川 成都 610041;2. 中國石油化工股份有限公司天然氣分公司, 北京 1001201;3. 中國石油天然氣股份有限公司新疆油田分公司采氣一廠, 新疆 克拉瑪依 834000

0 前言

隨著埋地管道在油氣輸送中應用日益廣泛,埋地管道在地震等地質災害中的安全問題受到極大關注[1]。而埋地環境受地質災害影響較大,分析其抗震問題較復雜[2-3]。

在位移控制載荷的管道設計中,例如滑坡、海底管道敷設和地震的情況,管道應力已超過屈服極限,此時采用以應變為基礎的設計更為合適[4-5]。該方法充分利用管材的抗變形能力,同時保持了結構的穩定性,主要應用于可能造成管線產生較大應變的地區,如地震多發區、凍土區。

對基于管溝參數的埋地管道抗震,國內外已有管線穿越斷層的管溝設計研究,本文以應變理論為基礎,從管溝設計方向來研究如何提高埋地管道的抗震性。

1 管土相互作用模型的建立

1.1 模型假設

1)根據埋地管道與地基土體的剛度特性,管道在地震時將伴隨周圍土體一起變形[6-7]。所以假定管道將承受與周圍土體同樣的縱向和橫向變形引起的應變。

2)在建立管土相互作用模型時,管道兩端位移約束對管道中間部位的反應影響很小,因此將管道兩端視為自由邊界[8]。最終分析截取管道中間段,這樣可忽略管道兩端邊界效應。

1.2 基本參數

管道:外徑1.219 m，壁厚0.022 m，管長600 m，管道材質X 80。

管材密度7 851 kg/m3,管材彈性模量210 GPa,管道埋深取2.0 m。

土壤:管溝采用砂土,密度18 kN/m3;內摩擦角為35°,管溝內土壤彈性模量30 MPa;周圍土21.8 m×13.3 m,彈性模量1 000 MPa;管溝坡度取10∶1;管溝底寬1.8 m。

管土之間摩擦系數0.38。

1.3 管土相互作用模型

對于埋地管道的研究,必須把管道周圍一定范圍內的土體作為結構的一部分加以考慮,即考慮管土相互作用問題[9];并且地震作用是通過周圍的約束土壤進行傳遞的[10-15]，因此本文首先建立了管土相互作用模型。

本文將土體簡化為四個方向的土彈簧:軸向土彈簧、水平方向土彈簧、垂直方向向上舉升的土彈簧和垂直方向承載土彈簧。

對于軸向土彈簧剛度的獲得，采取ASCE油氣管道抗震設計指南[16]來確定，經計算得到軸向土彈簧剛度為1.67×107N/m。水平橫向、垂直方向承載土彈簧的特性通過實際管溝截面內的平面應變有限元分析獲得[17]:水平方向土彈簧剛度為3.91×107N/m,垂直正方向土彈簧剛度為1.77×107N/m,垂直負方向土彈簧剛度為3.37×107N/m。

得到四個方向的土彈簧剛度,建立管土相互作用模型,管道單元共301個節點,每個節點處連接四個方向的彈簧,利用ANSYS軟件建立管土相互作用模型。

2 地震波的選取

管道一般埋于中硬土、中軟土中,由GB/T 50470-2017《油氣輸送管道線路工程抗震技術規范》[18]可知,地震波波速一般為150～500 m/s，本文地震波剪切波速取300 m/s;地震波加速度為0.2倍重力加速度,即0.2 g;地震特征周期Tg為0.35 s。

ANSYS軟件在解決地震波輸入問題時,有三種激勵途徑:用ACEL命令指定結構的加速度時程，大質量法，施加位移時程載荷[19]。為了能很好體現管線與土的相互作用變形,本文采用時間—位移關系時程載荷。

地基土體(周圍土體)的變形,可簡單地按表面波理論進行分析[20]。這樣地震時的地面運動非常近似于正弦波型的平面彈性波,此地面運動特性可描述為:

(1)

式中：y(x,t)為地震時地基土體的位移量，m;x為水平距離，m；t為時間，s；a0為地面運動的位移振幅，取0.1 m；T為地面運動的特征周期，取0.35 s；v為地震波的傳播速度，取300 m/s。

3 管道動力響應分析及其影響因素

3.1 加載和求解

對于管土相互作用模型,施加式(1)所示的正弦載荷。對該模型的求解,分別采用了一維加載和三維加載。

一維加載：分別對管道軸向(X方向)、管道豎直方向(Y方向)、管道橫向(Z方向)施加正弦位移載荷。

三維加載：同時施加X、Y、Z三個方向的位移時程載荷進行分析。

無論是具體的震害,還是大量的實驗表明,埋地管道受地震波作用時,管道的橫向響應遠遠小于軸向響應[21-22],因此以下的分析主要針對管道的軸向應變。

3.2 結果及分析

3.2.1 一維加載結果及分析

分別對X、Y、Z三個方向施加位移時程載荷,得到600 m管道150節點(約300 m處)的位移時程曲線，見圖1。

由圖1可以看出,只施加X方向位移載荷時管道位移最小,而分別施加Y、Z方向位移時程載荷時,二者的位移值比較接近,而且接近施加的位移載荷值。

圖1 分別施加X、Y、Z方向位移時程載荷時,管道中間節點位移時程曲線

三個方向分別施加位移時程載荷時,管道中間段(198～498 m)的最大軸向拉應變分別出現在管道的458、458、478 m處,最大軸向拉應變分別為13.68×10-4、3.60×10-4、5.04×10-4。由此可見,施加X方向的位移載荷產生的位移最小,而產生的管道軸向拉應變卻是最大的,因此施加管道軸向方向的位移時程載荷對管道影響相對較大。

3.2.2 三維加載結果及分析

圖2為管溝內管道模型。考慮到管道兩端效應,主要考察管道中間段的單元,如下列舉了管道150單元的軸向應變(圖2中5、13、21、29點)時程反應,見圖3～6。

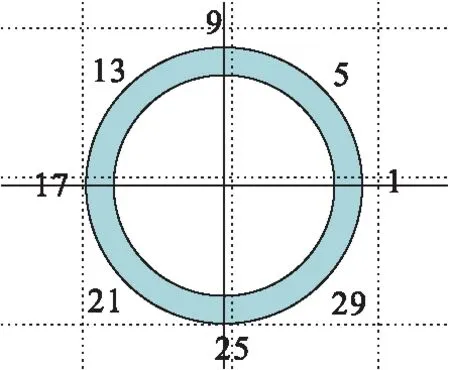
圖2 管溝內管道模型

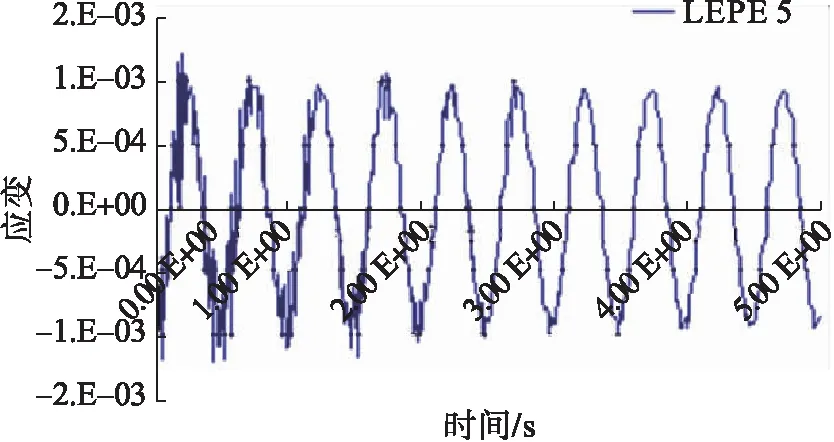
圖3 150單元截面的5點軸向應變時程曲線

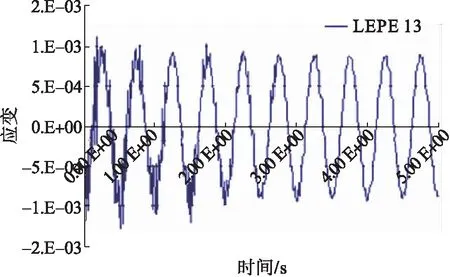
圖4 150單元截面的13點軸向應變時程曲線

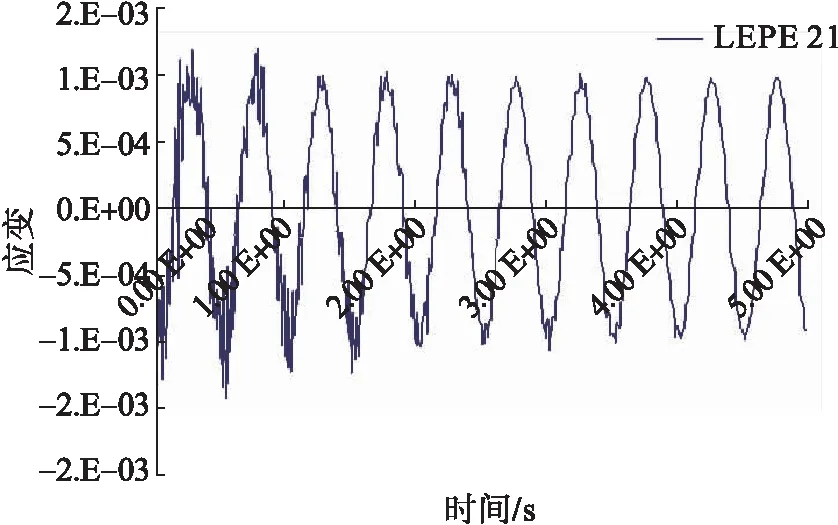
圖5 150單元截面的21點軸向應變時程曲線

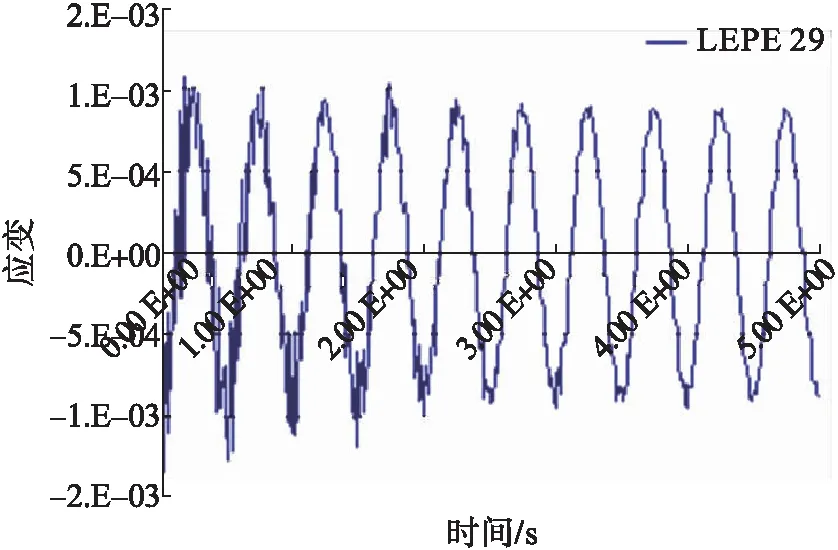
圖6 150單元截面的29點軸向應變時程曲線

圖3～6為管道150單元截面45°及135°方向的軸向應變曲線,基本呈余弦變化趨勢,與輸入的波形相似。

同時施加三個方向時程位移載荷時,管道產生最大軸向拉應變15.15×10-4,這比單向施加時程位移載荷所產生的最大軸向拉應變值都要大,并且與只施加X方向時程位移載荷所產生的應變值比較接近。在三個方向時程位移載荷同時作用時,對管道產生的拉伸作用更大。以下主要針對三個方向時程位移載荷同時作用時,對管道的影響因素分析。

3.3 影響因素分析

3.3.1 管道長度

考慮到管道長度對管道軸向應變的影響,對管土相互作用模型的管長分別取200、400、600、800、1 000 m來進行模擬,其它參數不變。

不同管長下,同時施加三個方向時程位移載荷。取中間段節點的最大軸向應變對比，見圖7。

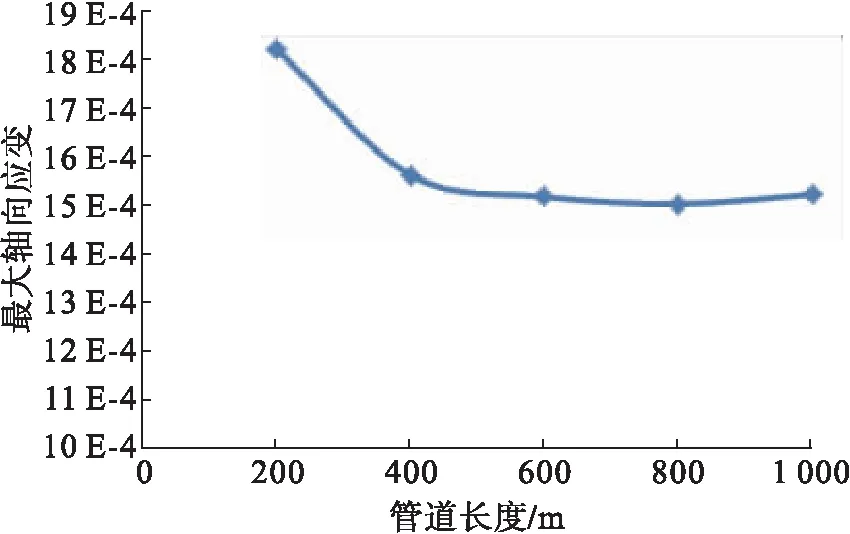
圖7 不同管長下,管道的最大軸向應變趨勢

由圖7可以看出,同時施加X、Y、Z三個方向載荷時,管道所產生的最大軸向應變值在管長為200～600 m時變化幅度較大,超過600 m后變化幅度較小。當應變值變化幅度小時,管長對管道最大軸向應變值的影響就較小。

另外,不同管長下,三個方向同時施加位移時程載荷,得到不同埋深下各管長中間節點的軸向最大正向位移值、最大負向位移值,見圖8～9。

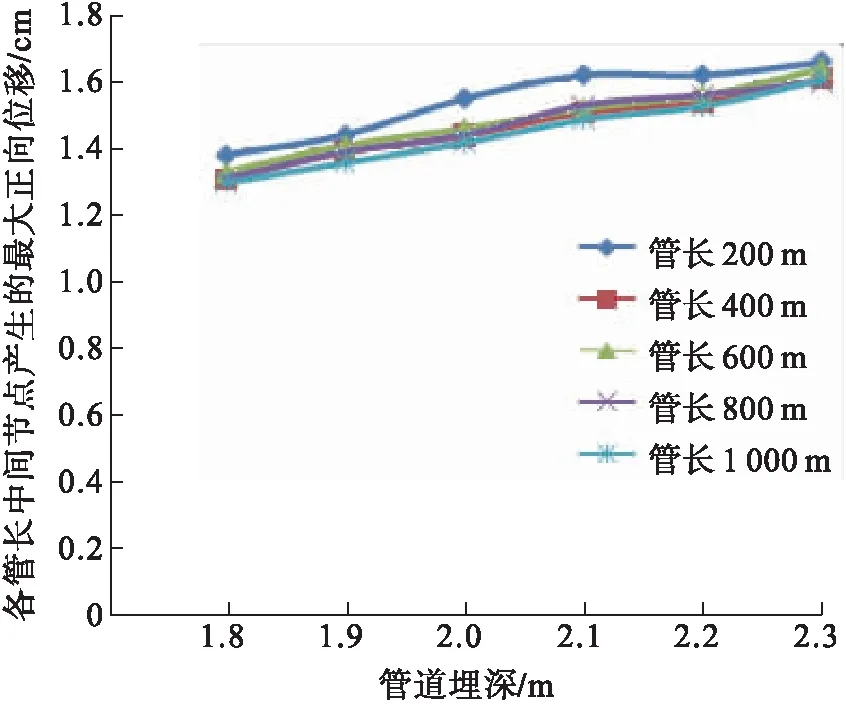
圖8 各管長中點正向最大位移變化趨勢

圖9 各管長中點負向最大位移變化趨勢

由圖8～9可以看出,管長200、400 m時,管長中點位移負向最大值的變化趨勢均不穩定,出現突起或凹下點,而管長大于600 m時,中間節點的最大正向位移值基本都很接近。可以看出,管長超過600 m時,管長對管道動力響應影響也較小。

因此進行管道的響應分析,只要管長取600 m,就可以忽略管長這一因素對結果的影響。因此后面分析其它因素對管道動力響應的影響時,管長均取600 m。

3.3.2 管道埋深

當管溝底寬1.8 m、坡度10∶1、土彈性模量30 MPa時,只考慮埋深因素對管道應變的影響。對管土相互作用模型同時施加三個方向載荷。取管道中間段節點(管段200～500 m)的應變值對比,得到管道軸向最大應變趨勢見圖10。

圖10 不同埋深下管道的最大軸向應變趨勢

3.3.3 管溝底寬

當管道埋深2.0 m,管溝坡度10∶1、土彈性模量 30 MPa 時,只考慮管溝底寬因素對管道應變的影響。

對模型同時施加三個方向載荷。取管道中間段節點(管段200～500 m)的應變值對比,得到管道軸向最大應變趨勢見圖11。

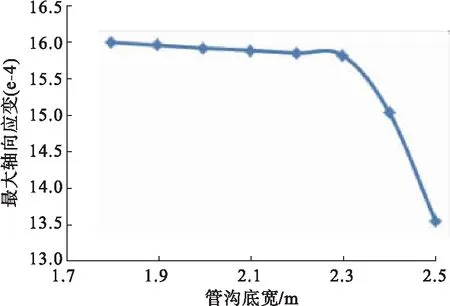
圖11 不同管溝底寬下管道產生的最大軸向應變趨勢

3.3.4 管溝坡度

當管道埋深2.0 m,管溝底寬1.8 m、土彈性模量 30 MPa 時,只考慮管溝坡度因素對管道應變的影響。對模型同時施加三個方向時程位移載荷。取管道中間段節點應變值對比,得到管道軸向最大應變趨勢見圖12。

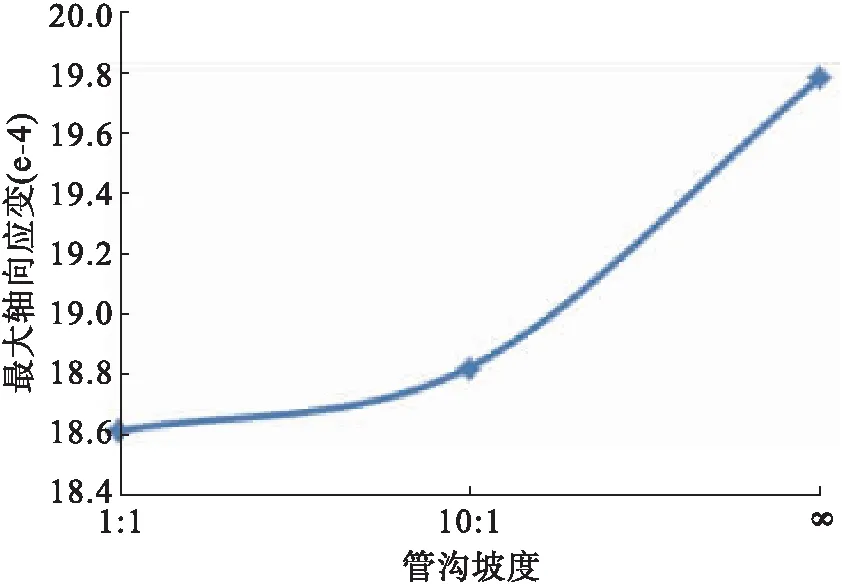
圖12 不同管溝坡度下,管道產生的最大軸向應變趨勢

3.3.5 管溝內土彈性模量

當管道埋深2.0 m,管溝坡度10∶1、管溝底寬1.8 m時,只考慮管溝內土彈性模量因素對管道應變的影響。對模型進行了三個方向加載。取管道中間段節點應變值對比,得到管道軸向最大應變趨勢見圖13。

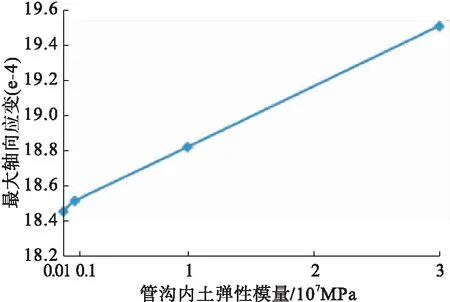
圖13 不同土彈性模量下,管道產生的最大軸向應變趨勢圖

4 結論

本文通過有限元軟件ANSYS建模,分析在地震波作用下各不同管溝參數對管道應變的影響,得出設計管溝的最優方案。

1)管道淺埋、管溝底寬大時利于抗震,考慮到經濟性,管溝底寬較大則施工難度加大,帶來了較大的工作量,因此在具體工況下可以適當調整。

2)土彈性模量較小的環境下管道拉應變比較小,因此將管道埋于土彈性模量較小的砂土環境利于抗震。

3)管溝坡度為1∶1時,管道軸向拉應變最小也最利于抗震。