山地城市跨江交通布局優化模型研究

喬 丹 任其亮 高春君

（1.重慶建筑工程職業學院，重慶 400072；2.重慶交通大學交通運輸學院，重慶 400041；3.重慶兩江新區建設管理事務中心，重慶 401122）

引言

江河孕育了人類文明，促進了城市產生，影響著城市的發展和變遷[1]。江河在為城市提供自然優勢、地理優勢和能源優勢的同時，也成為城市擴展與發展的天然屏障。

我國亦是一個多山的國家，有300余個城市以及10000余個建制鎮位于山區[2]。山地城市不僅是我國城鎮體系的重要組成部分，也是發展山區經濟的重要內容。

目前我國大多數山地沿江城市仍處于跨江發展階段，城市跨江發展意味著江河兩岸既作為一個有機整體，又相互獨立。跨江交通由城市的對外交通變為市區內部交通，這就要求跨江交通必須形成便捷迅速、高效暢通的綜合交通系統。

然而，山地城市跨江交通設施缺乏，跨江交通量分布集中，跨江交通往往成為山地城市交通網絡中的薄弱節點和擁堵源頭，因此，跨江交通布局優化問題是山地城市亟待解決的重要問題。

在山地城市跨江交通規劃建設中，如何充分考慮山地地形地貌特征與人類活動的關系，把跨江交通作為一個有機整體，而不是針對單一的橋隧規劃選址等問題，傳統的交通規劃理論與方法對此顯得力不從心[3]。

針對目前國內外對山地城市跨江問題的研究不夠系統和深入的現狀，筆者采用網絡圖理論描述山地城市跨江交通網絡，通過建立綜合跨江交通布局與跨江交通客流動態關系的雙層規劃模型，研究山地城市跨江交通布局優化問題，用改進的遺傳算法求解模型，并以典型的山地跨江城市重慶兩江新區為例，驗證模型的實用性。

1 山地城市跨江交通特征分析

山地城市獨特的地形條件造就了其特殊的用地布局和路網分布特征，使得山地城市在跨江交通運行和跨江交通流特征方面明顯有別于其他城市[4]。

筆者經過對山地城市跨江交通進行充分調研，得出山地城市跨江交通特征如下：

（1）用地布局特征。山地城市在用地拓展時往往趨向選擇地勢平坦、地質條件好的用地，用地布局呈現典型的多中心組團式。功能完整、相對獨立、自成體系的各個組團，共同形成山地城市多中心組團式的網絡城市結構。

（2）路網分布特征。山地城市多中心組團式的城市格局決定了山地城市路網大多為組團式、自由式布局，無固定的模式、固定的方向，組團內路網隨地形自由蜿蜒，道路的線性走向受地形影響較大；道路坡度較陡，橋梁架設較多；道路等級、功能劃分不明確，主次干道功能不清晰，同時呈現“高密度，低路幅”的特征。

（3）交通出行特征。山地城市由于組團間間距較大，交通出行特征明顯有別于其他城市，山地城市居民平均出行距離長，出行時間長，日均出行次數少，機動車使用比例較高。居民出行距離分布呈現雙高峰現象，即中長距離的出行比例比平原城市高。由于受地形影響，山地城市非機動車使用比例較一般城市低很多，居民出行時，基本不采用非機動車，因此，山地城市跨江公共交通分擔率相比其他城市要高。

2 山地城市跨江交通網絡描述

山地城市有特殊的地形地貌特征，為了描述山地城市跨江交通網絡，我們做出如下約定：

（1）區分兩種通道：跨江通道（cross-river channel）和沿江通道（river-side channel）；

（2）城市既是出行生成點也是目的地，跨江交通可以橫跨某區域之內；

（3）跨江交通方式有橋梁（BR）、隧道（TU）、索道（RO）、輪渡（FE）；

（4）旅客的車內時間定義為通道線路上車輛的行駛時間；

（5）每次跨江出行只能選擇一種交通方式，且不能中途改變；

（6）城市間的交通通行能力為各種交通方式在該路段的運能之和。

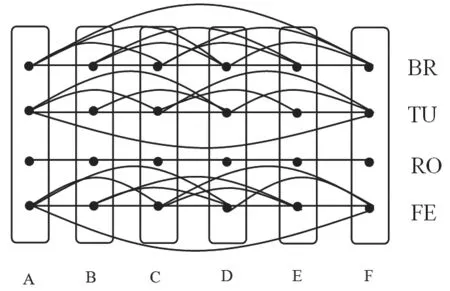
圖1 跨江交通基本網絡描述

圖1 為跨江交通基本網絡描述，該網絡描述能反映某城市跨江交通的交通流入和流出總量，可用節點、路段約束條件表示跨江交通的通行能力。同時，該網絡圖具有可擴充性，如增加通道內的城市節點數目，增加新的跨江方式等。

將圖1簡化，得到圖2，圖2中節點1、10分別表示起點和終點，節點2和6，節點3和7，節點4和8，節點5和9連接成的路段為跨江通道，節點2，3，4，5和節點6，7，8，9連接成的路段為沿江通道。起點和節點2，3，4，5分別連接而成的路段為起點連接路段。節點6，7，8，9和終點分別連接而成的路段為終點連接路段。

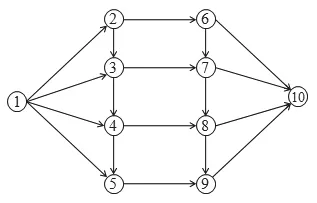
圖2 跨江交通網絡簡化圖

根據山地城市跨江交通特征，跨江交通布局優化問題主要包含兩個目標：第一，投資效用最大化的跨江交通新改建布局方案問題；第二，在新改建后的跨江交通布局方案上進行車流的分配，最大限度的滿足需求，并使得運輸費用最小化。

因此，跨江交通布局優化問題涉及到兩種不同目標函數的決策者，即：跨江交通規劃者和跨江交通用戶。

這兩者之間的區別是：規劃者處于主動地位，以網絡整體最優化為跨江交通規劃的依據，可以通過調整現有跨江交通布局來改變下層用戶的廣義運輸費用即出行成本；用戶處在從動地位，但是廣大的分散的用戶并不步調一致的服從規劃者的愿望，都是選擇最小阻抗或自以為是最小阻抗的路徑出行，即他們的決策依據是用戶最優，總體上的表現為：用戶均衡或隨機用戶均衡[5][6]。

然而，規劃者和用戶又不能完全獨立，這兩者之間的聯系是：用戶是在規劃者設計的網絡上進行均衡或隨機均衡分配，反過來，規劃者在確定各路段阻抗時只能依據用戶均衡分配或隨機分配的結果。

3 跨江交通布局優化模型

山地城市跨江交通規劃體現在交通網絡中若干條關聯通道的規劃，孤立地考察某一條跨江通道是否新建或改建難以體現出跨江交通網絡的整體性。因此，根據山地城市跨江交通問題的雙層性，筆者采用上層規劃者-下層用戶的雙層規劃模型研究跨江交通布局優化問題，其中上層問題為：從系統的角度（即從跨江交通規劃者的角度）考慮，在滿足投資等約束的條件下，使整個跨江交通的運輸總費用最小，即為特定車流分配的具有預算約束的投資模型。下層問題為：從用戶的角度考慮，使跨江交通路網上的用戶行為符合用戶最優準則，即規劃者為路網的配流模型[7]。

上層優化模型：

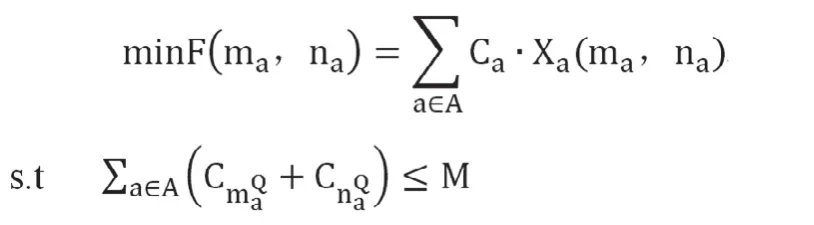
A1= {a | a = 1，2，…n} 表示已經存在的通道集合，A2= {a | a = n + 1，n + 2，…n + m} 表示備選的計劃新建的通道集合，a∈A為任意一條通道；Xa為通道a上的運輸量為新建通道的資金費用為改建通道的資金費用；M為特定的投資約束。

下層優化模型：

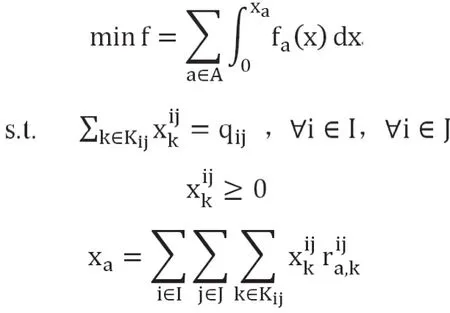
4 模型求解

山地城市跨江交通問題是一個多目標雙層優化問題，雙層規劃問題的求解是一個完全NP—Hard問題。至今關于求解城市交通NDP雙層規劃模型的研究，僅有一些初步結果。設計大規模雙層規劃的高效的全局最優算法一直是學者們努力研究的課題之一。由于遺傳算法具有多點并行搜索機制，不依賴于函數的可導性以及魯棒性等特點，筆者設計基于遺傳算法的混合智能算法來求解山地城市跨江交通布局優化模型[8]。

根據山地城市跨江交通的特殊性，對遺傳算法的參數作以下說明：

（1）確定待選優化方案。對于模型中的2個通道集合A1和A2，其中A1為既有通道集合，A2為擬新增通道集合，假設每個通道都與最近的節點直接相連，形成k條初始路線，在此基礎上可由規劃專家依據經驗再優選若干路段作為被優化方案，由此確定待優化單元。

（2）編碼。采用0-1二進制編碼構造染色體，本文優化方案中的跨江通道存在2種可能：新建或改建，對于集合A1中的變量a，0表示未建，1表示改建，對于集合 A2中的變量a，0表示未建，1表示新建。染色體長度為候選通道數量K。

（3）初始化種群。本文遺傳算法的初始種群采取隨機方式產生，算法改進的關鍵是，將同類型的變量放在同一神經元內，將不同類型的變量分開，根據需求選擇概率，以便合理控制子代的變化差異范圍。

（4）選擇。采用改進的輪盤賭選擇法。在選擇新個體時，首先在當前代中選擇最佳個體直接進入下一代（ 若有多個，則隨機選取一個） ，然后對其它個體依累積概率大小采用輪盤賭方式進行選擇。

（5）交叉。根據交叉概率進行交叉操作，采用多點交叉方法。

（6）變異。根據變異概率進行變異操作，采用單點變異方法。

（7）收斂性檢驗。若滿足迭代次數達到最大迭代數的收斂準則，則終止計算，否則返回步驟4。

根據以上分析，運用 mat lab編寫了山地城市跨江交通布局優化模型的遺傳算法程序。遺傳操作程序(部分)如下：

第一步：種群初始化，確保滿足約束的初始化。n=length(C0)；%決策變量的個數

種群初始化，每一行是一個樣本

farm=zeros(NU，n)；for i=1：NU

Ta=ran perm(n)；

Tb=unidrnd(n-1)+1；

farm(i，sort(Ta(1：Tb)))=1；

GT=farm(i，：)；

GT=JZU(GT，V，Q)；

farm(i，：)=GT；

end

輸出變量初始化

ALLX=cell（KU，1）；%細胞結構，每一個元素是N×n矩陣，記錄每一代的個體

ALLY=zeros（KU，NU）；%K×N矩陣，記錄每一代評價函數值

BESTX=cell（KU，1）；%細胞結構，每一個元素是1×n向量，記錄每一代的最優個體

BESTY=zeros（KU，1）；%K×1矩陣，記錄每一代最優個體的評價函數值

k=1；%迭代計數器初始化

5 實例分析

重慶市是典型的山城城市，主城區被兩江分割為北、中、南三大塊，城市布局呈組團式結構，跨江交通是重慶市城市交通的主要特征。重慶兩江新區是我國內陸地區唯一的國家級開發開放新區。

筆者以重慶兩江新區為例，應用上述方法進行跨江交通網絡布局優化，基礎數據包括現狀跨江交通網絡，跨江出行方式種類及成本，沿線兩側的人口密度，旅客跨江出行起點與終點及相應的客流量等基本信息。

本文以《2017年重慶市主城區交通運行分析報告》[9]和《2017年重慶市主城區交通發展年度報告》[10]的調研數據為基礎，結合現有通道的抽樣調查數據進行模型參數的標定。兩江新區現狀跨江交通網絡包含39個節點，16條跨江通道。跨江通道的全日交通量和高峰小時交通量為124.1萬pcu。

采用系統平衡模型進行各交通區之間的交通量分布預測，得出各交通區之間的產生吸引分布量，在此基礎上，結合增長系數，采用平均增長率法迭代未來OD交通量，通過將模型分別設定為2020、2025、2030年，結合未來年的流量分布，確定兩江新區跨江交通布局優化的實施方案。附表為兩江新區跨江交通布局優化備選方案參數。

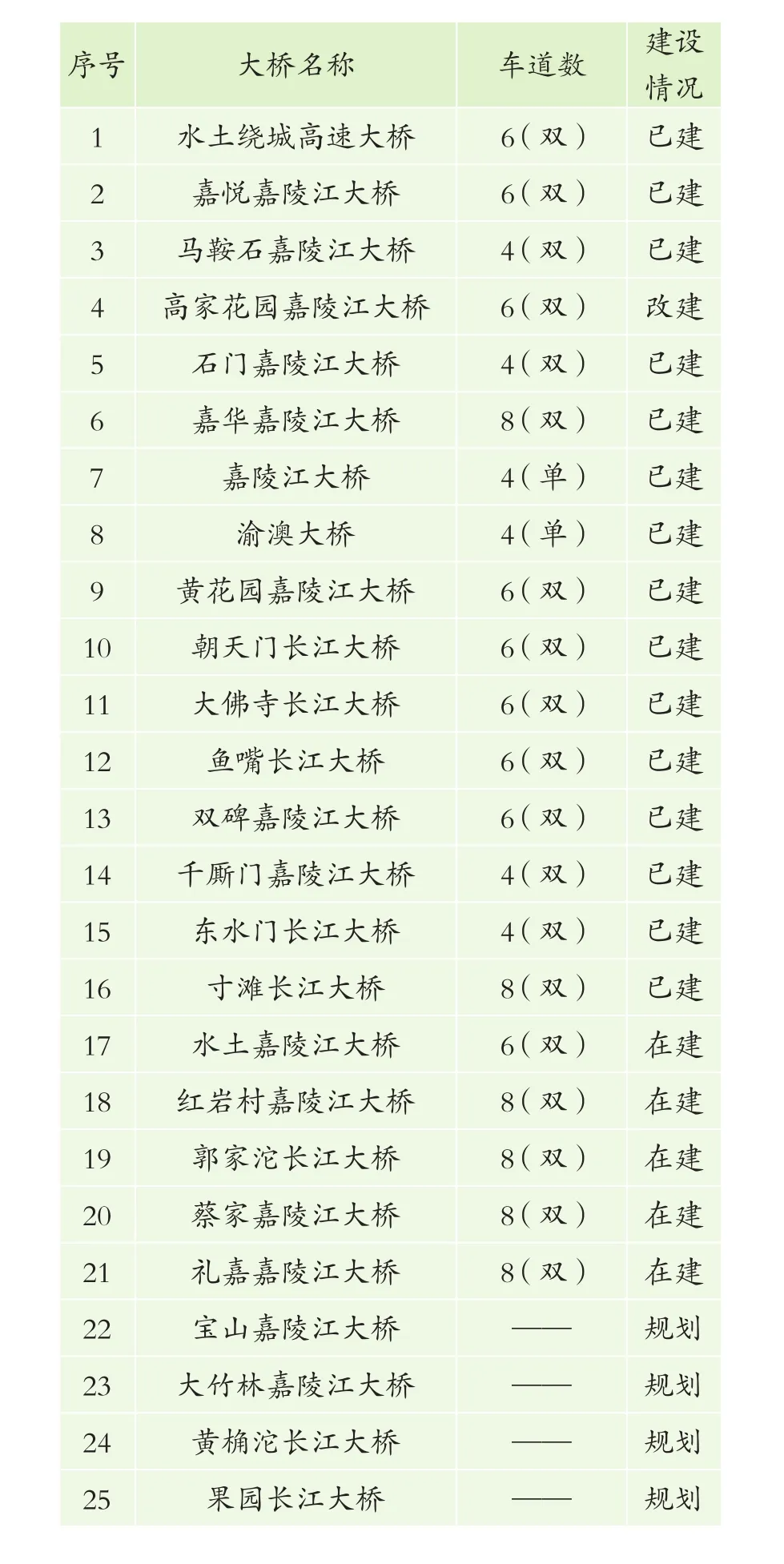
附表 兩江新區跨江交通布局優化備選方案參數

6 結論

本文建立山地城市跨江交通布局優化模型，對模型進行求解和實證分析，為現實中的跨江交通網絡布局優化方案的框架提供了輔助決策依據。重慶兩江新區跨江交通布局的實例優化結果基本符合區域內城市的發展路徑，表明本文研究結果有一定的現實參考意義。為了讓求解模型簡單易行，對部分要素進行了簡化并將一些參數設為定量，如投資成本費用等，這也是未來研究需要繼續完善的部分。