改進的Apriori算法的研究與應用?

李 龍 劉 澎 張可佳 黃 珊 李 倩

（東北石油大學計算機與信息技術學院 大慶 163318）

1 引言

數據挖掘是對大數據集的探索過程，并揭示出其中的隱含規律，它融合了眾多的技術，是計算機科學的一個重要分支［1］。利用數據挖掘技術進行數據分析，是一項極具現實意義的嘗試，它能夠加速理論知識到實際應用的轉化。其中關聯分析是數據挖掘中重要的分析技術之一，關聯分析是從歷史數據集中發現隱含模式，從海量數據集中發現潛在價值的方法，它反映過了一個事件與其他事件相互關聯的關系。

隨著信息化時代的到來，各類公司積攢了大量的數據，如何利用這些長期積攢的數據成為了主要問題［2］。本文主要針對股票的歷史交易數據進行挖掘，指導投資者合理購買股票，達到輔助決策的效果。

目前，部分研究學者提出了經典的Apriori關聯規則挖掘算法［3～5］，提出了股市中關聯規則挖掘方面的相關技術應用。本文在具體探究中的研究目標是挖掘頻繁項集中涉及到的Apriori算法，并將其改進。針對股票板塊聯動關聯規則挖掘這一問題，提出一種改進的Apriori 算法。在目前傳統Apriori算法的基礎上改進算法中數據庫的掃描次數，篩選出有用候選集，提高算法的利用效率。

2 改進的Apriori算法

目前研究學者提出的改進Apriori 算法［6～10］對掃描數據庫的次數與時間過程的考慮較少，對Apriori 算法的研究并沒有克服全部的局限性［11～15］，沒有做到將Apriori算法的運算時間效率提高。

本文在深入研究傳統的Apriori算法的基礎上，提出一種改進的Apriori-L 算法，優化頻繁集的計算過程，提高算法的運行時間效率，對二項頻繁集數目超過二項的頻繁集方面的操作在具體實踐應用中起到關鍵性的意義。

2.1 算法描述

綜合性的結合Apriori 算法在學術界中相關的研究過程和現有的實驗結果分析，可知算法在運算掃描過程中耗費時間多［16～20］，篩選候選集是s函數，同時也是計算支持度的函數和產生過頻繁項集的函數，進一步分析算法在運算過程中耗費時間長的原因主要有以下兩方面：

1）候選集過多的問題。在頻繁集生成候選集的過程中，即由k-1生成k的過程中，利用關聯規則得到所有k 項集合作為候選集，部分K 項集存在對算法結果無用的現象。此時，這些無效的K 項集會造成算法時間的耗費。

2）算法在整個掃描操作中會產生比較多的掃描次數。在相關的掃描事務集、支持度的分析與計算、頻繁集的獲取操作中，算法應用中的循環次數與候選集數量兩者之間的關聯性有很強的關系，如果候選集的數量龐大，直接影響算法在運行過程中的時間效果。

綜上所述，針對目前傳統Apriori算法在具體應用中所存在的不足之處，本文結合實際問題制定出科學可行的改進算法-Apriori-L 算法。改進后算法的主要思路如下：

1）首先，將一項頻繁集L 獲取到，并與每一個事務集進行合并操作，找出每個事務集中頻繁性小的數據，將其刪除，獲得W。

2）其次，在W中找出所有的二項子集cu。

3）再次，二項候選集z 由cu 生成，將二項候選集z 作為關鍵值存入一個h 表中。如果h 表中己經存在將要存入的關鍵值，把與這個關鍵值相對應的v值在應用中加1處理；若h表中沒有所需存入相關關鍵值，需要把key 直接存儲在h 表中按照專業性的流程有效處理，同時將其對應的v值變成1。

4）最后，在h 表中將關鍵值變成二項候選集z，關鍵值對應的v即為該二項候選集z的支持度。

2.2 算法分析

假設事物集a中的事物項的數量為b，n為平均元素在事物項中，L1代表的是一項頻繁集在算法應用中的實際數量。

假設O（n）指的是各個事物項在算法操作中和頻繁集所有時間的復雜度，O（Cn2）代表的是二元子集在具體操作中的時間復雜度情況，O（1）是指存入表與v值在操作中加1的時間復雜情況。

基于上述綜合性的分析可知，在進行二項候選集Cz獲取時，將支持度進行綜合性分析計算的操作過程中，Apriori-L的時間復雜度表示如下：

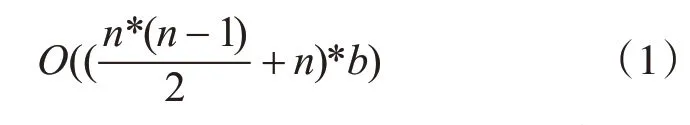
對上述步驟按照專業性的規范流程進行掃描，即可有效地獲取到候選集的支持度h 表s，并對每一個候選集在算法應用中的支持度和最小支持度關系的時間復雜度進行判斷并表示如下：

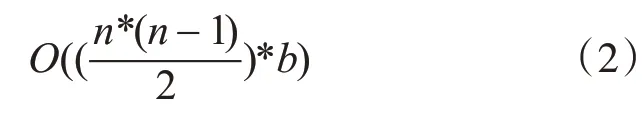
由式（1）、（2）可知，Apriori-L 在生成二項頻繁集的過程中的時間復雜度為

通過綜合性的對比分析，能夠明確地推斷出Apriori 算法在形成二項頻繁集過程中的時間復雜度情況。

在進行二項候選集C2 獲取的算法操作時所對應的時間復雜度表示如下：

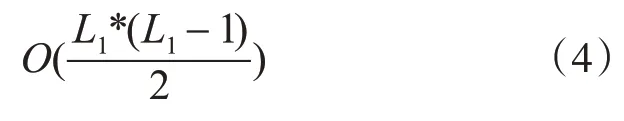
事務集的掃描、支持度的分析計算以及頻繁集選取所對應的時間復雜度表示如下：

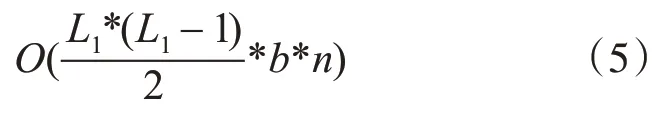
由式（4）、（5）可知，Apriori 算法在生成二項頻繁集的過程中的時間復雜度為

綜上所述，可知Apriori算法在運算過程中比改進的Apriori-L 算法需多運算L21，對比分析Apriori算法與Apriori-L 算在的時間復雜度表示情況能夠明確的推斷出，Apriori-L算法在進行二項頻繁集生成的操作中，能夠科學精確地獲取到L21/n 在算法應用中的加速效果，可提高算法的使用效率。

Apriori算法在生成二項頻繁集時，時間復雜度與L12有重要的關系，一項頻繁集數量L1直接影響算法的運行效率，如果L1數量特別多，則算法的使用效率變低。而在Apriori-L 算法中，生成二項頻繁集的過程與L1關聯性不大，與事務項中的元素平均數量n 的關聯性較強，n 作為事物集中的平均數量，n 小的情況下，該算法可以對算法的運行效率產生較好的影響，即提高運行效率。在實際生活中，有許多一項頻繁集數量大于事物集中平均元素數量的基本現象。比如說，水果超市中銷售的水果類別要超過平均每一位顧客所選購的水果類別的實際數量。

3 Apriori-L算法的實際應用

股票模塊是按照上市的股票進行的分類，主要包括行業、概念、地區等方面，本文主要對30 個模塊采取科學的方式進行關聯性分析操作。這些模塊在算法應用中主要涉及到酒店餐飲、旅游、石油和電力等諸多專業性的模塊。把模塊聯動看為一個模塊的漲和跌和另外一個模塊的漲和跌相互影響。對于投資者來說獲取模塊的聯動信息的價值十分重要。利用經驗去判斷模塊間的關系缺乏科學依據，如旅游行業和酒店餐飲行業兩個模塊通過經驗可以分析出具有一定的關聯性，可是關聯的強度靠經驗較難判斷。現有的挖掘股票數據的方法主要有Apriori算法，利用此算法可以得出確切的模塊間聯動信息，指導投資者進行股市投資，幫助股市投資者及時規避風險。

本文在具體分析中采取科學的理論提出了改進的Apriori算法，實踐操作中對各行業模塊間的所存在的關聯規則有效的挖掘，與以往探究板塊間關系的方法具有很大差別，本文在原有研究方法的基礎上，對不同模塊的漲跌幅度聯動性結合實際情況綜合性的探究，根據在實踐應用中的每一種漲跌幅其模塊之間的關聯性的數據挖掘，對于股市投資者全面明確模塊之間的聯動的關聯規律起到直接性的促進作用。

3.1 數據預處理

對板塊每一天的具體漲幅情況進行綜合性的分析計算，深入化的探究海量的測試數據集在算法應用中的數據分布狀況，將每個模塊的漲幅劃分為6 個部分：0＜幅度＜0.01；-0.01＜幅度＜0；0.01＜幅度＜0.03；-0.03＜幅度＜-0.01；幅度＞0.03；幅度＜-0.03。板塊的幅度在實踐操作中能夠均勻有序的歸入到這6 個種類中是主要的劃分準則。按照專業性的規范標準將幅度區間有序的劃分，為每一個模塊所對應的幅度區間合理的排號。表1 是每日的模塊數據的具體轉化情況。

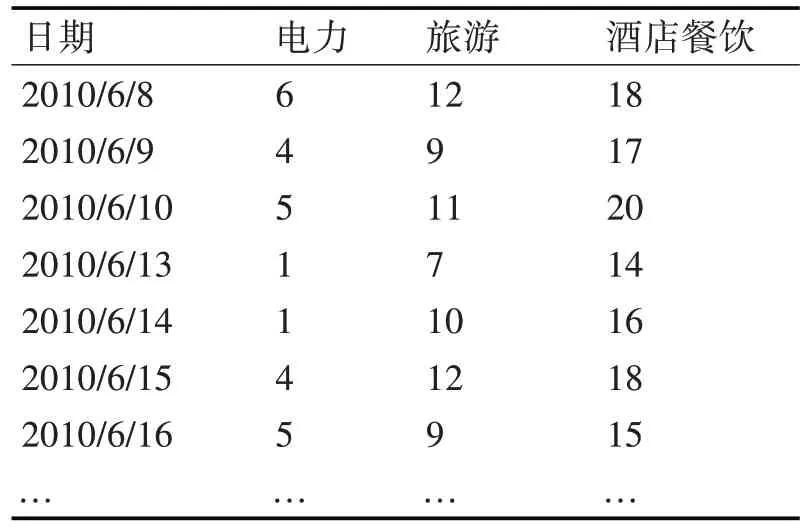
表1 部分模塊數據

綜合性地把排號和數字6 科學的運算所獲取到的值與數字6 中的某種狀態是相互對應的。處理好的數據后存入到數據庫中。對處理后的數據采用sql進行檢測，結果如下：

1）未在數據中發現空值、冗余值，2322 條記錄與2322 天30 個板塊指數的情況一一對應，完整性良好。

2）利用統計方法，找出所有板塊每天的漲幅幾乎均落在6 種狀態下。因此可知漲幅區間的劃分是合理有效的。

3.2 頻繁項集

通過對不同的最小支持度的調整，對Apriori算法以及Apriori-L 算法分別科學的分析與挖掘數據的頻繁集。

基于各種支持度的實際情況可知，圖1 是原始Apriori 算法和Apriori-L 算法在二項頻繁集計算過程中相關運行時間的具體示意圖。

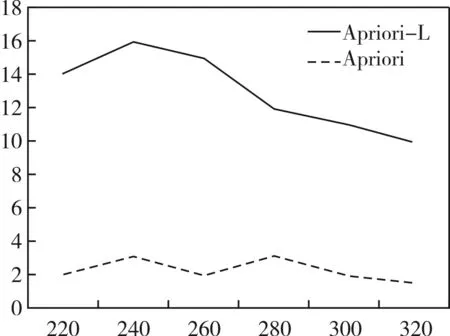
圖1 不同支持度下的運行時間

支持度320 下，Apriori算法和Apriori-L 算法在進行關聯規則算法應用中總時間和二項頻繁集時的時間計算的綜合性對比情況如下圖2 和圖3 所示，其中a為計算二項頻繁集時間，b 為計算關聯規則總時間。

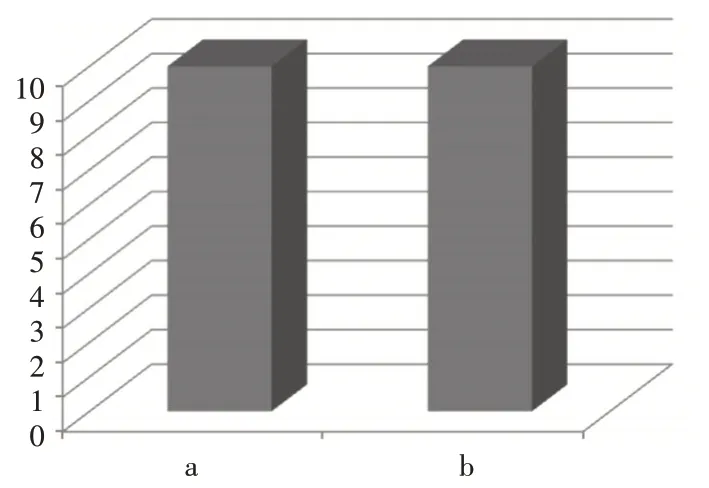
圖2 Apriori算法

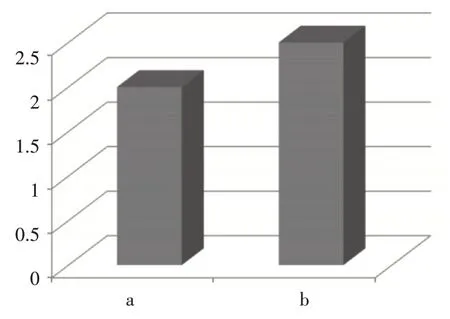
圖3 Apriori-L算法

由圖2、圖3 的實驗結果可知，在支持度320下，改進后的Apriori-L 算法相比較原Apriori 算法可提高算法中二次頻繁集的計算時間效率值約為81.5%，可提高算法總體運行時間效率值約為78.5%。

綜上可知，Apriori-L算法的性能與原始Apriori算法相比有很強的優勢，Apriori-L能夠在實踐應用中展現出較強的算法功能特性。

3.3 計算關聯性

在實踐應用中選取支持度320 下的相關頻繁集，結合實際需求將置信度設置為0.8，在此基礎上采取專業性的操作方式計算關聯規則，獲取到如表2所示的具體計算結果。

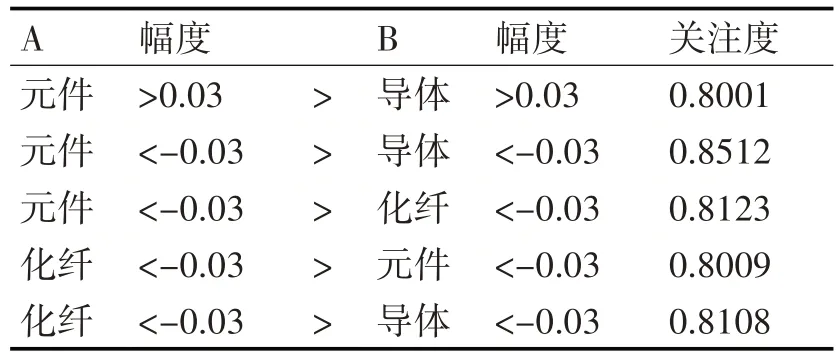
表2 部分模塊聯動性

在計算關聯規則的綜合性操作過程中能夠有效地獲取到元件、導體、化纖這三個主要的板塊在漲幅區間中具體的關聯規則情況。如果元件漲幅超過0.03，導體模塊可能大于0.8001 的漲幅情況會超過0.03。所以投資者在觀察到元件漲幅超過0.03時，可以對導體模塊加強關注。

與根據模塊的是否漲跌來進行關聯挖掘相比，新的基于漲跌幅關聯挖掘可以排除股市小幅正常漲幅的影響；獲得信息也更加具體精確，相同模塊中的不同漲跌幅度在一定程度上和不同的模塊會產生聯動作用。

4 結語

對股市的歷史數據進行關聯規則的挖掘分析對股市的投資者具有重要的指導意義。Apriori 算法作為挖掘頻繁項集最重要的一種算法具有較好的意義，但是算法運行效率有一定的缺陷性。本文提出的Apriori-L 算法先分析時間復雜性，再在分析的基礎上找出在人們日常生活中的實際性，在彌補算法不足的基礎上將算法應用到實際中發現本文的方法對提高算法的運行效率具有一定意義。本文將提出的算法應用到股市模塊聯動性的挖掘中，改進后的Apriori算法能夠快速發現不同股票模塊的不同幅度之間的聯動規則，可為股市投資者提供數據信息支持，為決策提供數據支撐。