發展學生數學“思維建模”能力策略摭談
董志俊 王英姿
一、問題提出
筆者在教學中常遇到下述狀況:(1)學生對數學問題的解題策略體現出“無章法”,學生在解題時的指向性與組織性不強;(2)學生對一些問題的解決過程中呈現出“碎片化”,學生不能把相關知識有效地整合在一起,而是處于一種似懂非懂的狀態;(3)學生對一些問題的細節處理“欠優化”,解題時往往事倍功半,容易迷失方向,也很難體現數學的簡潔美。
以上的狀況說明,當學生遇到問題時,缺乏一套相對完整的應對策略,筆者認為“思維建模”能很好地解決上面提出的問題。
二、國內外研究借鑒
“思維建模”的概念最早是由美國密蘇里大學的教育專家喬納森(David Jonassen)教授系統提出。喬納森在《技術支持的思維建模:用于概念轉變的思維工具》一書中認為:思維建模通過思維建模工具幫助學習者具化內部的認知概念模型,促使學習者在建模的過程中積極地調整與修改自我的概念模型結構,并通過多種形式的認知呈現,幫助學習者豐富和拓展內部認知概念模型的意義。有意義的學習需要概念參與,學習的目標就是概念的轉變與發展;對學習者來說,支持有意義學習最有力的策略之一是對他們所學的知識進行模型的建構,思維工具的使用可以看作是能引發和支持概念轉變的建模工具。喬納森的這些思想在整個世界產生了很大的影響。
國內目前也已有部分學者專家對思維建模的理論進行了關注及研究。北京師范大學劉儒德在《建模:一種有效的建構性學習方式》的文章中提出,建模作為一種建構性學習方式,可促使學習者根據先前的知識經驗,使用所給的物件和工具,來探究當前情境,建構起對當前情境的理解,并將自己的這種理解表達出來,從而可促進學生對知識的深層理解和靈活應用。劉教授還具體將建模分為探究性建模和表達性建模兩種形式,并提出了關于建模的三種抽象水平,即定量、半定量和定性;他同時強調,在教學中,教學者可根據學生的發展水平,提供適當的支持,幫助學生展開不同形式、水平的建模活動。此外,郭秀霞在《淺析思維建模工具對學習者思維品質的培養》一文中著重對思維建模(思維建模也是一種思維工具)和思維品質做出理論性的研討。
本文中的“思維建模”強調通過對數學經典問題及相關知識和結論的剖析,從中提煉關鍵詞,建構思維過程,讓學生不斷積累數學基本活動經驗,在遇到新問題時,可以快速提取關鍵信息,形成有效的解決策略。
三、探析思維建模途徑
思維建模不是知識建模,是對學生知識內化過程建立的模型。如何才能實現知識的最優組合與新知識網絡的構建,促成學生數學思維的提升,是每一位教師都值得思考的問題。筆者對此進行了一些探究,具體過程如下:
1.挖掘關鍵詞,形成知識鏈。
數學是一門非常嚴謹的學科,每一個字、每一詞都有確切的含義。在高中數學教學中,教師要“字斟句酌”,將每一個字、每一詞的意義講清楚。例如,在教學“函數”概念時,通過對“非空”“任意”“唯一”等幾個關鍵詞的分析,能進一步加深學生對函數概念的理解。
提煉關鍵詞除了可以幫助學生認識到數學語言的嚴謹性,也可以讓學生構建問題解決的知識鏈。學生在學習新知識和做練習題時,首先要進行讀文、讀圖。在讀的過程中要找關鍵詞,把所找到的關鍵詞進行勾畫、批注。這一步可操作性強,通過長期落實,學生自主閱讀能力自然提高。關鍵詞的提煉是思維建模的前提,學生整合以往所學數學知識和數學經驗,從知識、方法和思想三個維度去探索問題的解決方案。具體如圖1所示。
2.剖析經典,設計題組。
美國科學哲學家庫恩認為學生正是通過學習范例,通過做習題等活動來掌握一門科學知識及其方法,沒有范例,科學知識就不能清楚地表達出來。設計題組是思維建模的關鍵。題組是具有內在聯系的一組習題,一般先易后難,問題背景可以不同,但核心知識是相同的。思維建模需經歷“感知—感受—感悟”一系列過程,在題組設計上充分考慮學生思維的最近發展區,切合教學實際。在課堂實施中要注重學生的主體性和教師的主導性,讓學生積極主動參與教與學的全過程,從而促成各個層次學生思維的發展。
例如,在人教版高中數學必修二中有如下3道習題。
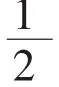
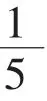
(3)已知點 M(x,y)與兩定點 M1,M2的距離之比是一個正數m,求點M的軌跡方程,并說明軌跡是什么圖形。(考慮m=1和m≠1兩種情形)(P144)
以上3道題都涉及平面到兩個定點的距離之比是不等于1的正常數的點的軌跡,其共同的數學背景就是經典的軌跡——阿波羅尼斯圓。教學中可以在分析三道題目共性的基礎上,歸納引出阿波羅尼斯圓,并設計如下兩個引申習題。
問題 1:已知平面向量 a,b,c 滿足|a|=3,b+c=2a,且|b|=|b-c|,若對每一個確定的向量b,記|b-ta|(t∈R)的最小值為dmin,則b變化時,dmin的最大值為_______。
問題2:四棱錐P-ABCD滿足AD⊥平面PAB,BC ⊥ 平 面 PAB,AD =4,BC =8,AB =6,∠APD=∠CPB則四棱錐P-ABCD的體積最大值為_______。
設計類似題組,能讓學生學會對經典題型和知識點的歸類,可提升學生的數學思維建模能力。
3.理清思維脈絡,構建邏輯框圖。
學生的數學認知過程是一個建構的過程,在數學認知方面需要培養建構思維,建構數學概念、定理、公式、命題以及蘊涵其中的思想方法。為此,提升學生構建數學思維建模能力的第3個策略,是幫助學生形成邏輯框圖,理順解題思路與策略。
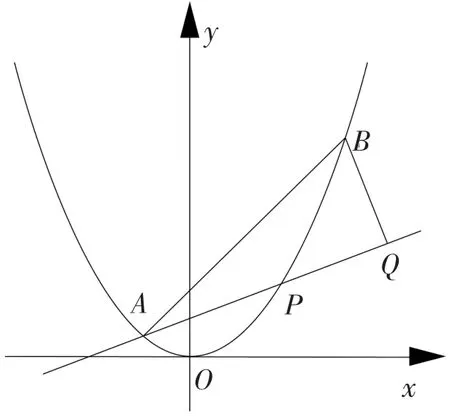
(圖2)
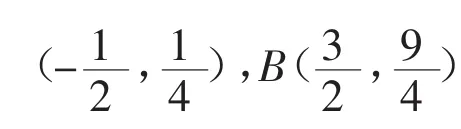
在教學時要引導學生通過關鍵詞“垂直”,縱橫鏈接相關知識點,構建解題邏輯框圖。如圖3。
綜上,數學思維建模能力的提升是一個逐步的過程。學生的思維建模有助于學生思維品質的培養,實現“人人都能獲得良好的數學教育,不同的人在數學上得到不同的發展”的目標。
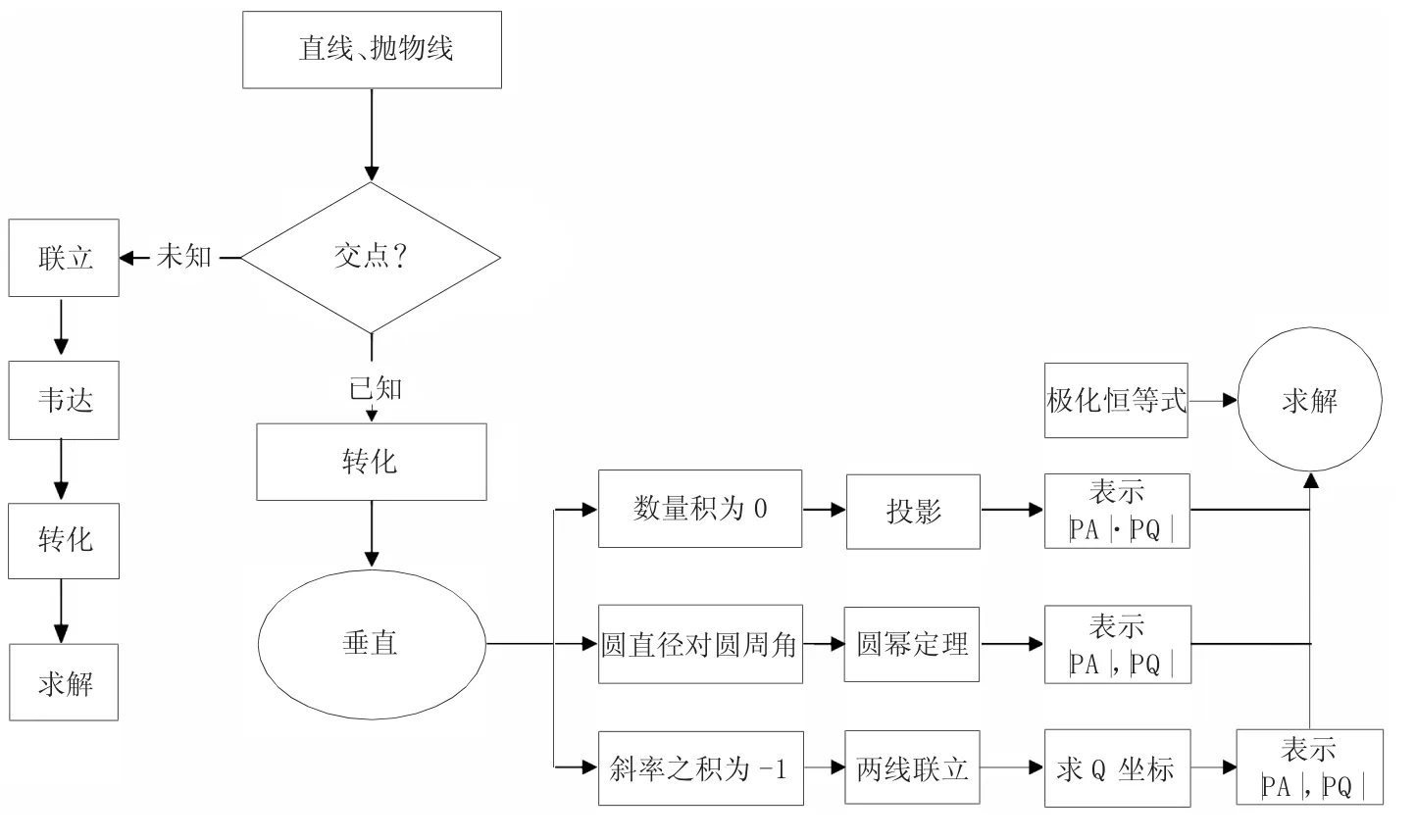
(圖3)

