聚類算法結果的可視化分析方法?

魏振鋼， 鄭東輝， 魏兆強

(中國海洋大學信息科學與工程學院，山東 青島 266100)

聚類結果的好壞與原始數據集的相關屬性具有一定關系，而聚類得到的相關數據都是一些不容易理解的數字信息，很難從中得到數據簇拆分重組、數量變化、聚類結果穩定性等信息。研究聚類結果的可視化方法能夠發現聚類過程中的相關規律，對數據挖掘和聚類的相關研究具有重要意義。

然而，目前聚類相關研究仍然依靠單純的數據集的聚類結果數據分析，難以發現其中的相關規律和內在聯系。文獻[1-3]中對聚類結果的分析比較詳細，但是很難發現聚類結果的穩定性與數據集中的維度關系。文獻[4]中提出了一種聚類結果可視化的分析方法，是一種基于matlab中dendrogram而改進的方法，可以看出聚類變化的過程，但是不能發現聚類結果與維度的關系、數據簇數量的變化，本質上還是一種dendrogram。目前的可視化方法主要缺點[5-11]：(1)無法顯式表現數據集聚類結果穩定性與數據屬性的關系；(2)無法展示數據簇在聚類過程中數量變化。如圖1所示，dendrogram只能表現出數據集聚類過程中數據簇重組情況，無法表現聚類結果與數據屬性的內在聯系以及數量的變化。

本文提出的PC方法，能夠提供一種顯式的方法對聚類結果進行分析，容易表現數據集聚類變化過程、數據簇的數量變化，發現聚類結果與數據屬性的內在聯系。即PC方法能夠很好的記錄和表現聚類過程中數據簇的數量變化、拆分和重組等情況，對聚類研究具有重要作用。

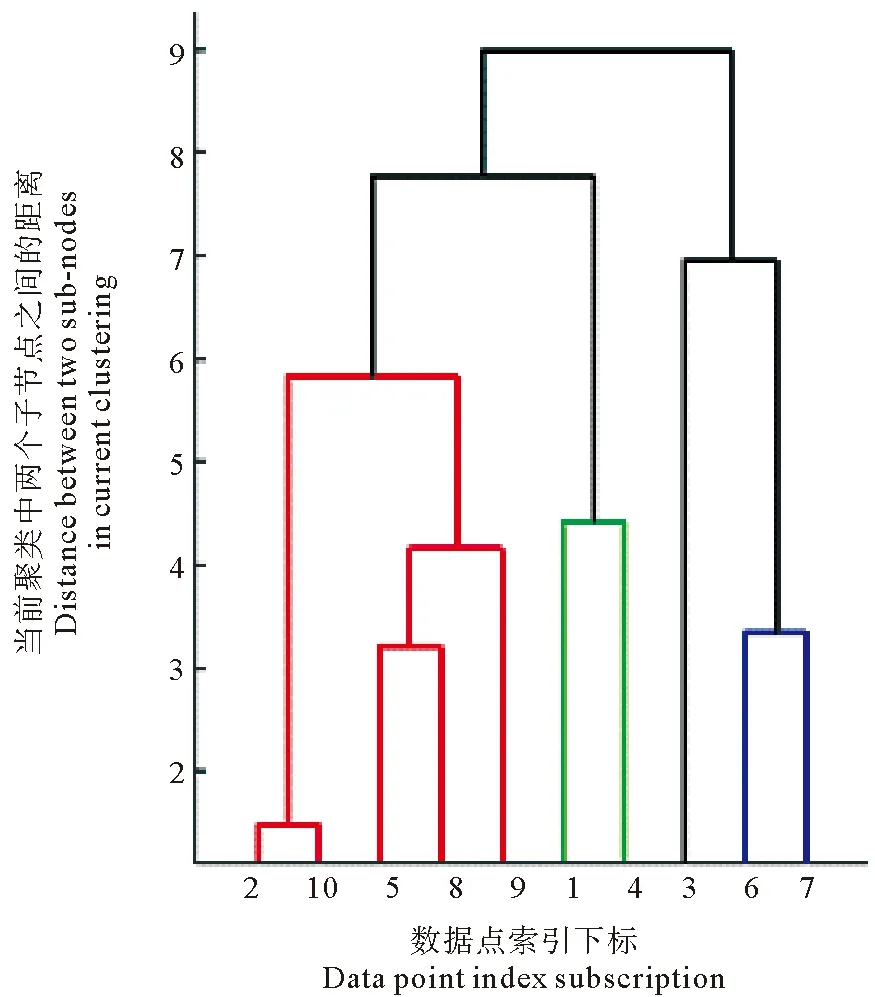
圖1 matlab中dendrogram

1 PC聚類結果可視化分析方法

PC方法的基本思想是記錄數據集聚類過程中的一系列矩陣，利用圖的形式直觀的表現出聚類結果與某個屬性的關系和聚類過程中數據簇的變化，圖中矩形塊的長度表示聚類結果中數據簇的數量，相近類別的矩形塊之間的連線表示數據簇的拆分和重組關系以及變化過程。數據簇拆分后組成其他數據簇，然后從不同的數據簇分出一部分組成新數據簇，這種情形越多，PC圖中交叉現象就越嚴重，說明聚類結果的穩定性越差。通過這種直觀的描述，根據數據簇的拆分重組情況，評價聚類結果穩定性與某個屬性是否有一定的關系。

通過對不同聚類數k下聚類結果的分析，得到一個原始數據的分類矩陣，該矩陣包含了每個原始數據被分到了相應類別的信息，然后將此分類矩陣通過PC技術以更加直觀的圖表方式表現出來。具體實現如下：

輸入：數據集X={x1,x2,x3,…,xn}；

輸出：聚類結果的PC圖。

①通過調用聚類算法，得到數據集聚類結果的類別矩陣

(1)

式中：k=1,2,3,…,7,代表對數據集聚類數目；1～k數據集中這一條記錄屬于1～k中的某一類；n代表數據集記錄的數量。

②把得到的類別矩陣合并為一個矩陣

首先初始化HB矩陣：

(2)

經過k次聚類，然后通過公式合并矩陣

(3)

式中，n代表數據集數據的數量，n≥0且n為整數。

③通過HB矩陣統計目前k聚類結果與k-1聚類結果的對應關系，存儲聚類過程的矩陣記為重組矩陣

初始化矩陣TJX，如下：

(4)

式中k代表聚類的類別數。

然后運用下面公式計算TJX矩陣。

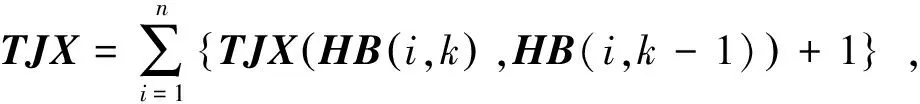
(5)

式中n為HB矩陣中的行數。

④利用HB矩陣統計矩陣中的相同數值，計算統計矩陣

(6)

式中k代表聚類的類別數。

⑤計算聚類數目為i時矩形條的高度的一半

(7)

式中：GD為設定的值，代表數據集記錄數量，值越大，PC尺寸越大；i為此時的聚類數目。

⑥初始化存儲此前矩形塊的坐標和長度矩陣

(8)

式中，H為矩陣TJ的行數。

⑦循環畫出代表每簇數據的矩陣塊,并記錄此次循環的相關數據，計算矩陣塊的長度

(j-1)×0.5，

(9)

式中，j為此前的聚類數目，j=1,2,…，H。

使用matlab自帶的rectangle公式畫出矩形塊

rectangle(′Position′,[0.95+(i-1)×1.0,JS,

(10)

式中i為此時的聚類數目。

利用ZBH矩陣存儲此時的矩形塊的長度和坐標

ZBH(j,1)=JS，

(11)

(12)

⑧循環畫出矩形塊之間的變化過程：

根據TJX矩陣計算矩形塊之間的變化數量

(13)

式中：m=1,2,…,H；n=1,2,…,i；CH為HB矩陣的記錄數量。

調用matlab中line函數畫出數據簇之間的變化過程

line([1.05+(i-2)×1.0,0.95+(i-1)×1.0],[ZBQ(n,1)+ZBQ(n,2),ZBH(m,1)+ZBH(m,2)])，

(14)

line([1.05+(i-2)×1.0,0.95+(i-1)×1.0],[ZBQ(n,1)+ZBQ(n,2),ZBH(m,1)+ZBH(m,2)-SGD])，

(15)

ZBQ(n,2)=ZBQ(n,2)-SGD，

(16)

ZBH(m,2)=ZBH(m,2)-SGD，

(17)

其中，

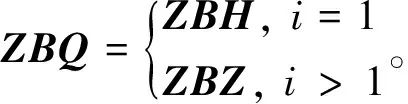
(18)

2 實驗結果及分析

2.1 數據集介紹

本文實驗的數據集包括自行設計的人工數據集Balls和2個UCI數據集，各數據集的基本信息如表1所示。

表1 數據集的基本信息

2.2 實驗結果及分析

2.2.1 對Balls數據集的分析 本次實驗選擇的數據集是一系列二維的坐標點，用PC方法進行分析。本文用的聚類方法是譜聚類，也可以采用其他聚類算法，在此不做累述。下面是數據集Balls，如圖2所示。

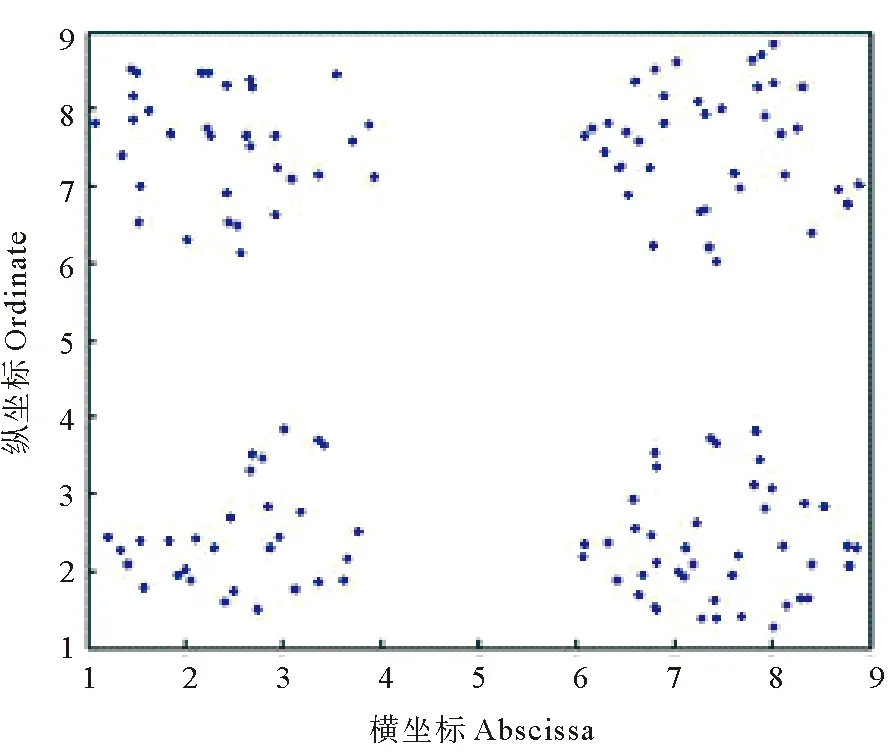
圖2 balls數據集

在實驗中，使用PC方法進行計算分別得到了x維度的PC(見圖3(a))和y維度的PC(見圖3(b))。

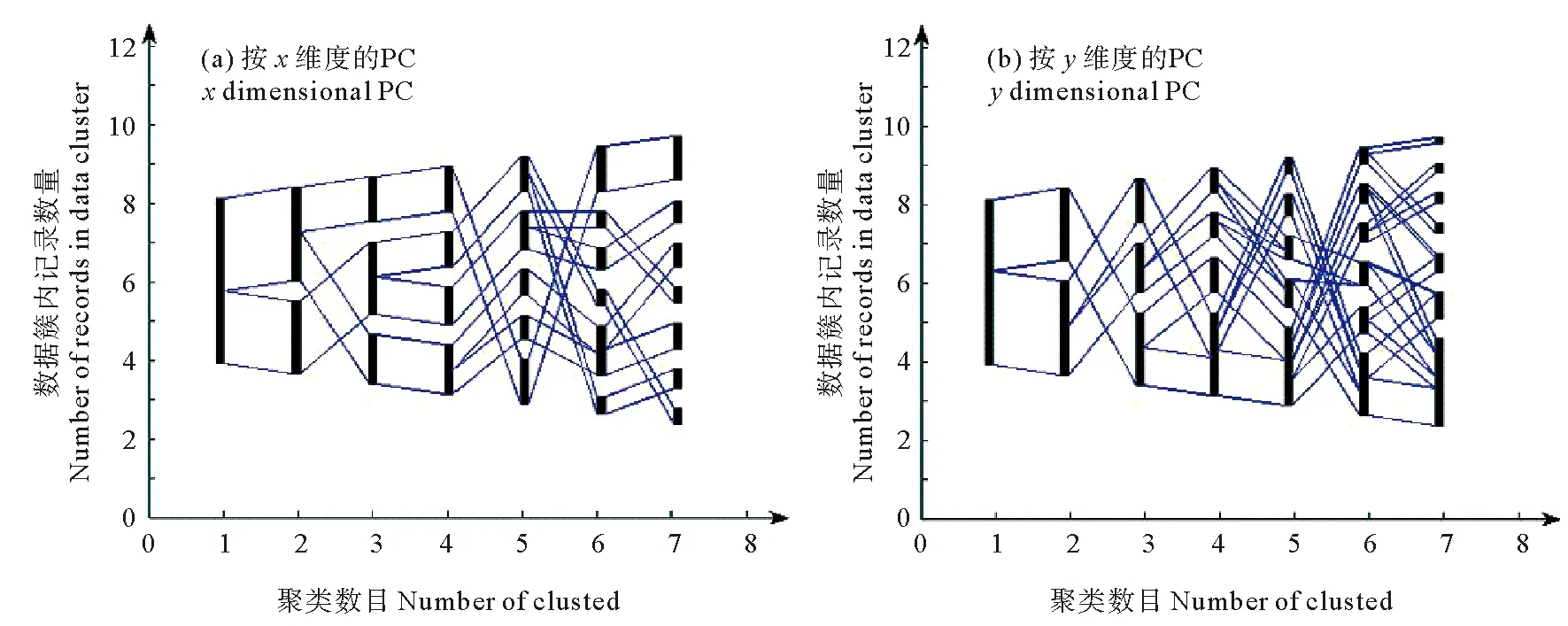
圖3 balls數據集按不同維度計算得到的PC

按x維度得到的PC從數據簇為4時開始，往后的拆分重組不多，交叉不多。而按y維度得到的PC從數據簇為4時開始，往后的拆分重組現象比較嚴重，交叉復雜。通過比較上述兩種情形，能夠很容易的看到數據集在y維度的聚類過程中，數據簇的拆分重組現象比較嚴重，判斷出balls數據集按x維度聚類效果比按y維度聚類效果好。

2.2.2 對UCI其他數據集分析

(1)對數據集glass的分析 通過PC可視化算法對數據集glass進行分析，分別得到了9維度的PC(見圖4(a))和2維度的PC(見圖4(b))，判斷出glass數據集按2維度聚類效果比按9維度聚類效果好。

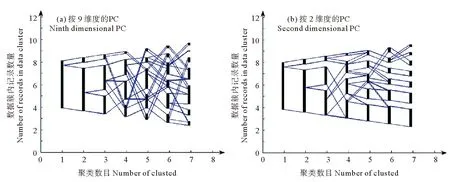
圖4 glass數據集按不同維度聚類的PC

(2)對數據集heart的分析 通過PC可視化算法對數據集heart進行分析，分別得到了2維度的PC(見圖5(a))和7維度的PC(見圖5(b))，判斷出heart數據集按7維度聚類效果比按2維度聚類效果好。

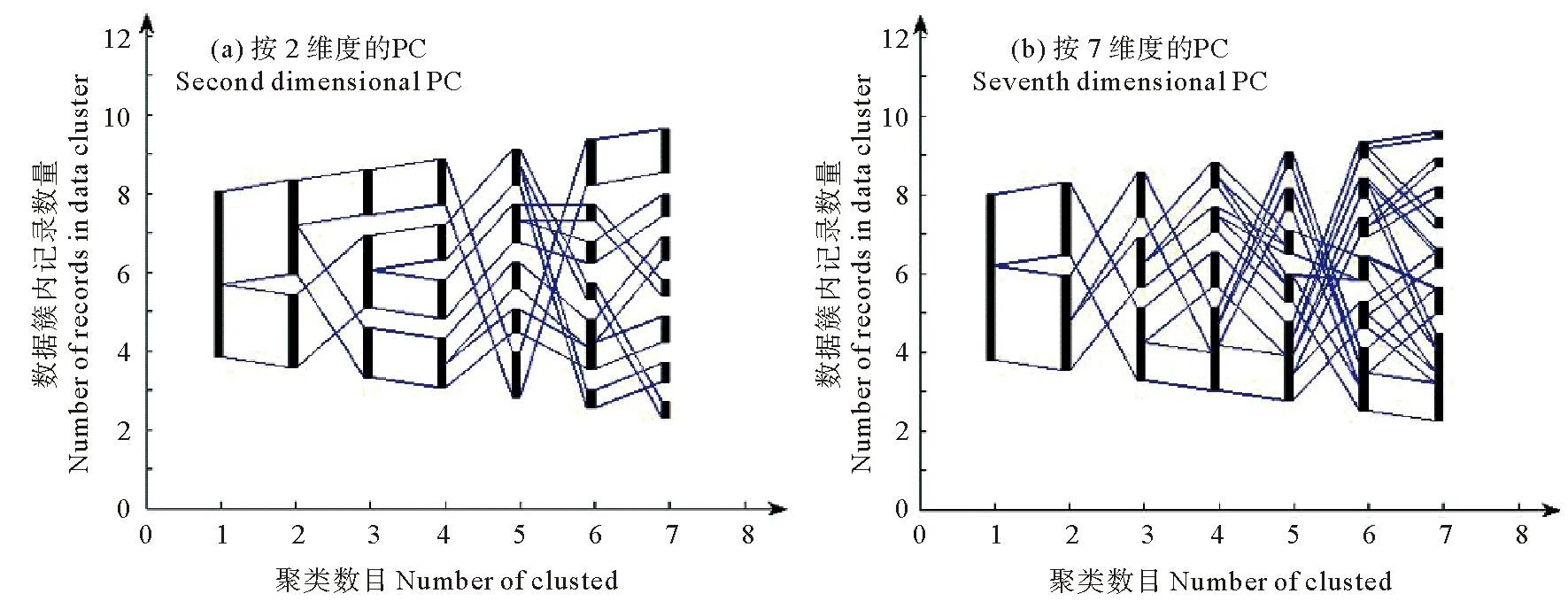
圖5 heart數據集按不同維度聚類的PC

3 結語

本文運用PC方法針對不同的數據集進行實驗，能夠展現出聚類的過程中數據簇的拆分和重組情況，很容易地發現其他可視化算法不能展現出的聚類結果穩定性與不同維度的數據之間的規律，極大的提高了聚類分析的效率。