基于圖的粗糙集屬性約簡方法

米據生,陳錦坤

(1.河北師范大學 數學與信息科學學院, 河北 石家莊 050024;2.河北省計算數學與應用重點實驗室,河北 石家莊 050024;3.閩南師范大學 數學與統計學院,福建 漳州 363000)

自1982年Pawlak[1]提出粗糙集理論以來,該理論已成為一種有效處理不確定和含糊信息的重要數學工具。在數據挖掘、機器學習和知識發現等領域有重要的應用[2-5]。

由于在現實數據集中,往往存在大量冗余和不確定性的信息,嚴重影響到后續數據挖掘和處理的效率。因此,如何高效地去掉冗余信息,已成為當前數據分析處理的一個熱點問題。作為粗糙集理論的一個重要應用,屬性約簡已經被證明是一種有效的數據約簡方法。它通過刪除冗余屬性,能獲得數據集合的本質信息和保持原始數據分類信息的完整性,從而提高數據的分類質量。

基于區分矩陣和布爾推理方法計算所有的屬性約簡或最小約簡已經被證明是一個NP-hard問題[6]。因此,各種高效的啟發式約簡算法被提出[7]。這些啟發式的約簡算法主要是尋找一個約簡或近似約簡。常用的啟發式約簡算法主要包括:基于區分矩陣的約簡算法[8-10];基于正域的約簡算法[11-13]和基于信息熵的約簡算法[14-17]。關于粗糙集的屬性約簡方法的系統闡述可參閱綜述文章[7,18]。

目前粗糙集屬性約簡方法的研究已經取得了很多成果。然而,這些算法在處理大規模數據集,尤其是面對高維數據時,效率仍然不夠理想。針對以上問題,本文提出一種新的屬性約簡框架。主要是受到文[19-20]的啟發,從圖論的角度出發,對決策信息表的區分矩陣給出直觀和等價的刻畫,最后利用極小頂點覆蓋方法獲取決策表的屬性約簡。數值實驗結果表明,所提出的基于圖論的屬性約簡方法在面對較大規模數據集時具有有效性和高效性。

1 基本知識

1.1 屬性約簡

定義1[21]稱S=(U,A)是一個信息系統,其中U和A分別是非空有限論域和屬性集;對于任意的屬性a,稱a:U→Va是信息函數,滿足:?x∈U,a(x)∈Va,其中Va稱為屬性a的值域。

對任意的B?A,記

IND(B)={(x,y)∈U×U|a(x)=a(y),?a∈B},

顯然IND(B)是U上的一個等價關系,也稱為不可分辨關系,它能導出U上的一個劃分:

U/B={[x]B|x∈U},

其中,[x]B={y|(x,y)∈IND(B)}稱為x關于IND(B)的等價類。

給定一個信息系統S=(U,A)和X?U,X關于IND(B)的下、上近似分別定義為:

定義2[21]決策表是一個特殊的信息系統S=(U,C∪g0gggggg),其中C為條件屬性集,d?C為決策屬性。記IND(d)是由決策屬性d所導出的等價關系,而U/d是由IND(d)生成的劃分。

設S=(U,C∪g0gggggg)是一個決策表,定義如下不可分辨關系:

IND(B|d)={(x,y)∈U×U|(?a∈B,a(x)=a(y))∨(d(x)=d(y))}。

稱B是S的一個約簡,若滿足:

所有約簡的交稱為S的核心屬性集。

定義3[22]設S=(U,C∪g0gggggg)是決策表,?x,y∈U,稱

M(x,y)=

為x與y的區分集。所有的區分集可形成一個對稱矩陣M,稱為決策表S的區分矩陣。

利用區分矩陣,便可以定義相應的區分函數,從而獲得所有的約簡集。

定義4[23]設M為決策表S=(U,C∪g0gggggg)的區分矩陣,則稱

fM=∧{∨M(x,y)|?x,y∈U,M(x,y)≠?}

為M的區分函數。

1.2 圖的極小頂點覆蓋

一般地,一個無向圖可表示為一個二元組G=(V(G),E(G)),其中V(G)是圖G的頂點集,E(G)是圖G所有邊的集合[25]。為簡單起見,一般可把圖簡寫為G=(V,E)。圖G中邊的端點若重合為一個頂點,則稱為環。若兩條邊有相同的端點,則稱這兩條邊是平行邊或重邊。稱圖H是圖G的子圖,記為H?G,若滿足V(H)?V(G)且E(H)?E(G)。設G1和G2是圖G的兩個子圖,稱G1∪G2為圖G的并圖,其頂點集和邊集分別為V(G1)∪V(G2)和E(G1)∪E(G2)。給定圖G的頂點v,dG(v)表示G中與頂點v相連接的邊的數目,稱為頂點v的度。

定義5[25]設G=(V,E)是給定的圖,K?V。若K能覆蓋圖G的所有邊(即E的每條邊都與K中的某個頂點相連接),則稱頂點子集K是圖G的一個頂點覆蓋。進一步地,對于任意的v∈K,若K-{v}不是圖G的頂點覆蓋,則稱K是圖G的極小頂點覆蓋。

類似于求決策表的所有約簡,圖的所有極小頂點覆蓋也可以通過構造相應的布爾函數獲得[20,25]。

fG=∧{∨N(e)|?e∈E},

N(e)是與邊e∈E相連接的頂點集。

2 基于圖的屬性約簡框架

2.1 決策表的誘導圖

定義6[19-20]設S=(U,C∪g0gggggg)是決策表,M是S的區分矩陣,為了方便,用e∈M表示e是矩陣M中的元素。記

V=C,E={e∈M|e≠?},

則稱GS=(V,E)是決策表S的誘導圖。

從定義6可以看出,決策表S的誘導圖實際上是以決策表的條件屬性作為頂點集,而以區分矩陣M的非空元素作為邊集。它是對決策表的區分矩陣的一種直觀刻畫。通過這種刻畫,以及利用引理1和引理2,易知決策表S的所有屬性約簡集與該誘導圖的所有極小頂點覆蓋集是相同的[19-20]。從而,求決策表的屬性約簡問題可轉化為求相應的圖的極小頂點覆蓋問題。這為粗糙集的屬性約簡方法提供了新的視角和方法。

例1表1是一個決策表S=(U,C∪g0gggggg),其中U={x1,x2,x3,x4},C={a1,a2,a3}。由定義3,可獲得其區分矩陣M(見表2)。在表2中,a2a3表示集合{a2,a3}。從而,由引理1,易知S有兩個約簡集,分別為{a1,a3}和{a2,a3}。

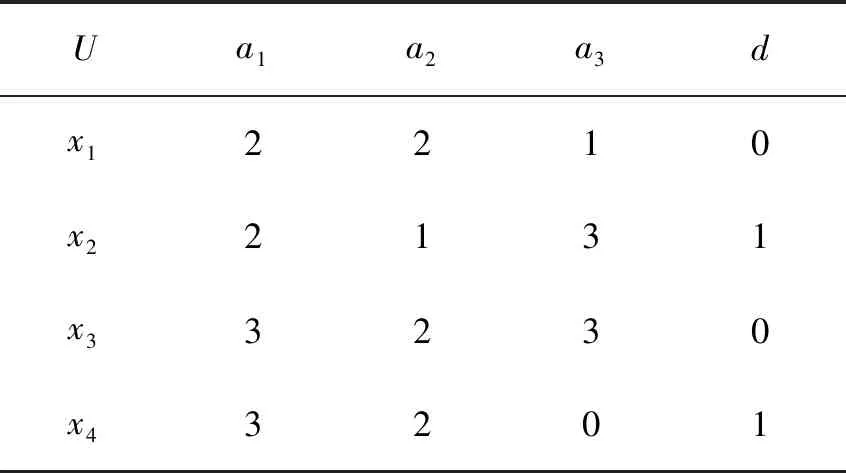
表1 例1的決策表Tab.1 A decision table of Example 1

利用定義6,其誘導圖GS見圖1。在圖1中,GS共有4條邊,對應了區分矩陣M的4個非空且不重復的元素。

表2 表1的區分矩陣Tab.2 Discernibility matrix of Tab. 1

圖1 表1的誘導圖Fig.1 Induced graph of Tab.1

由于區分矩陣M是對稱矩陣,并且M中往往有很多重復的元素。定義6蘊含了去掉這些重復的元素。因此,定義6所導出的圖是不包含平行邊的。實際上,如文獻[20]所述,利用吸收律,上面的誘導圖可以進一步的簡化。

由于平行邊對獲取圖的頂點覆蓋沒有影響,因此,為計算的方便,可以得到下面更一般的誘導圖(見定義7和圖2)。

定義7設S=(U,C∪g0gggggg)是決策表,M是S的區分矩陣。記

V′=C,E′=M-{?}

定義6和定義7中所定義的兩種誘導圖的區別僅僅是去掉一些重復的邊(或平行邊)。實際上,圖1可看成是圖2的簡化(或子圖)。而且,這兩個圖的極小頂點覆蓋集是相同的(見性質1)。記C(G)表示圖G的所有極小頂點覆蓋集。

圖2 表1的一般誘導圖Fig.2 General induced graph of Tab.1

證明由定義6、定義7和引理2即可證得。

性質2GS=(V,E)是決策表S的一般誘導圖,若a∈C是S的核心屬性,則a在圖GS中是帶環的頂點。

證明由相關的定義即可證得。

2.2 一般誘導圖的分解和約簡方法

定義7所給出的一般誘導圖本質上是對決策表的區分矩陣的刻畫。但是一個決策表的區分矩陣往往需要O(|U|2|C|)的存儲空間,這也意味著生成整個誘導圖也需要O(|U|2|C|)的存儲空間。這對于具有較大樣本集的決策表而言,易因存儲空間的不足而導致其算法極其低效。因此,本文避免生成整個誘導圖,而是通過局部的思想,對其子圖進行分步處理。

定義8設GS=(V,E)是決策表S=(U,C∪g0gggggg)的一般誘導圖。對于任意的x∈U,記

Vx=V,Ex={M(x,y)|y∈U},

則Gx=(Vx,Ex)是GS的一個子圖。

證明由定義3、定義7和定義8即可證得。

定理1表明決策表的一般誘導圖可分解為一些子圖的并。

例2在例1中,對于x1∈U,其子圖Gx1見圖3(a)。顯然,Gx1是GS(圖2)的一個子圖。由圖2,易知GS恰好分解為4個子圖。

圖3 GS的子圖Fig.3 Subgraphs of GS

證明由定義8和定理1即可證得。

3 基于圖的屬性約簡算法

由上一節的理論結果,本節將設計相應的啟發式算法來獲得決策表的主要屬性。通過改進經典的圖頂點覆蓋算法[26],我們有下面基于圖的粗糙集特征選擇算法。

算法1基于圖的粗糙集特征選擇算法1(GRF1)

輸入:決策表S=(U,C∪g0gggggg)

輸出:一個屬性約簡Red

1) Red=?

2) 生成誘導圖GS=(V,E);∥根據定義6

whileE≠?

v0=arg max{dG(v)|v∈V};

Red←[Red,v0];

去掉E中被Red所覆蓋的邊,并仍記為E.end while

3) for每個v∈Red

if Red-{v}能覆蓋簡化圖G的所有邊

Red←Red-{v};

end if

end for

算法1(GRF1)的空間復雜度是O(|U|2|C|),與其他基于區分矩陣的約簡算法的存儲空間基本是一致的。其次,GRF1的時間復雜度是O(|U||C|)。與其他大部分的約簡算法相比,GRF1顯然更加快速。但是面對大規模數據集,尤其是含有較大樣本的數據集時,GRF1容易因為內存不足而導致無法運行。

算法2基于圖的粗糙集特征選擇算法2(GRF2)

輸入:決策表S=(U,C∪g0gggggg)

輸出:一個近似屬性約簡Red

1) Red=?

2) for 對每個x∈U

生成子圖Gx=(Vx,Ex);//定義8

Red←[Red,v0];

end while

end for

算法2(GRF2)的時間和空間復雜度都是O(|U||C|),與其他基于區分矩陣的約簡算法和GRF1相比,其存儲空間降低了很多。這將會極大地提高GRF2的運行效率。但是與GRF1相比,GRF2不一定獲得一個真正的約簡,它所獲得的特征數目往往比GRF1多。

4 實驗結果與分析

實驗選用了8個公開的數據集進行驗證。具體的數據集描述見表3。在實驗中,我們選取了3種具有代表性的約簡算法進行對比,它們分別是基于區分矩陣的約簡算法SPS[10]、基于正域的約簡算法FPR[13]和基于信息熵的約簡算法FCCE[13]。本文所有的實驗結果均在Windows 10 (i7-6700,CPU 3.40 GHz,內存24GB)的普通個人PC上獲得,使用的操作平臺是Matlab2016b和Weka3.8。

具體的實驗結果如圖4、表4、表5、表6、表7和表8所示。圖4展示了GRF1和GRF2這兩種算法在生成相應的圖時所需要的存儲空間。從圖4可看出,GRF2所需要的存儲空間比GRF1小很多,比如,對于數據集Chess,GRF2所占用的存儲空間僅僅是GRF1的0.13%。對于擁有大樣本的數據集而言,這種差異往往會更加明顯。以數據集Letter和Relathe為例,算法GRF1會因為“內存溢出”而導致程序無法運行。實際上其他基于區分矩陣的算法也往往具有這種現象。比如,算法SPS,雖然它已經去掉了區分矩陣中一些不必要的元素,但是對于較大規模的數據集比如Letter而言,它仍然會因為內存的不足而導致無法獲得實驗結果。因此,與其他基于區分矩陣的屬性約簡算法相比,GRF2更適合于處理大規模的數據集。實際上,GRF2和FPR,FCCE等算法的存儲空間復雜度都是一樣的。它們都適合于處理大樣本的數據集。

表4記錄了5種算法在這8個數據集上的運行時間。在表中,“*”表示由于該算法“內存溢出”而導致的程序無法運行。從表4中可看出,GRF1和SPS適合于處理高維小樣本的數據集。FPR和FCCE適合于處理低維大樣本,而GRF2不管什么類型的數據集,其運行速度均表現得極其高效。以Relathe數據集為例,GRF2的運行時間分別是FPR,FCCE和SPS的0.46%,0.46%和0.30%。這些結果進一步表明GRF2是一種高效的特征選擇方法。

表5列出了具體的約簡結果。從表中可知,與其他算法相比,GRF1和FCCE均能獲得極小的屬性子集。實際上它們均能獲得一個真正的約簡集。

而GRF2只能獲得一個協調集,平均而言,GRF2獲得的特征子集的屬性個數是最大的。然而,對于大部分的數據集而言,這種差異并不是很大。

表6,表7和表8分別記錄了這5種算法在約簡前后的分類精度。在這些表中,“Full”表示約簡前原始數據的分類精度。所有的分類精度均在Weka3.8上采用10折交叉驗證獲得,實驗中采用了3種分類器:CART,SVM和PAPT。實驗結果表明,與原始數據集的分類精度相比,這些約簡算法均能獲得較好的分類精度。這也表明這些算法能提取一些重要的特征。與FPR,FCCE和SPS相比,GRF1和GRF2獲得較好的平均分類精度。尤其是GRF2,在大部分的數據上,均能獲得最好的分類精度。

表3 實驗數據集Tab.3 Data sets for test

圖4 算法GRF1和GRF2的存儲空間Fig.4 Storage spaces of GRF1 and GRF2

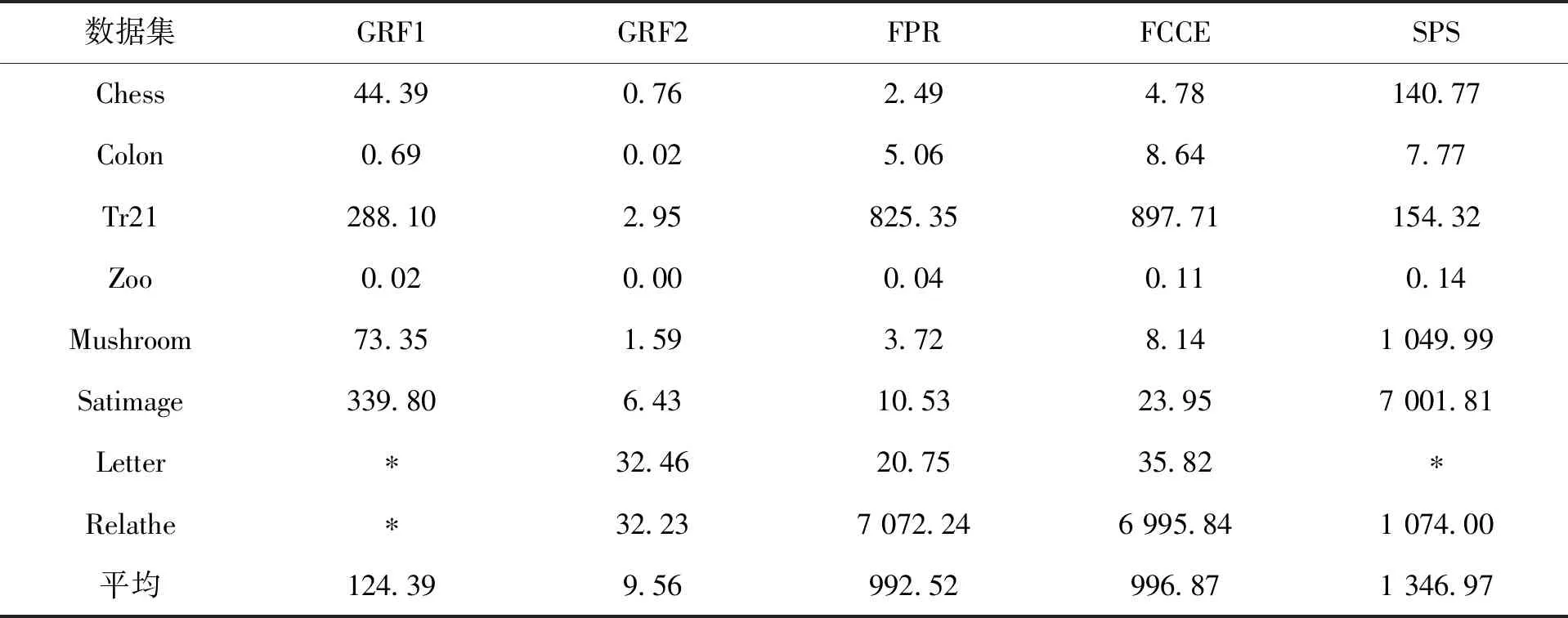
秒/s

表5 約簡結果Tab.5 Results of reduct

表6 分類精度(CART)Tab.6 Classification accuracy (CART)

表7 分類精度(SVM)Tab.7 Classification accuracy (SVM)

表8 分類精度(PAPT)Tab.8 Classification accuracy (PAPT)

5 結 語

本文基于圖的頂點覆蓋方法提出了一種粗糙集屬性約簡模型。該模型對經典粗糙集的區分矩陣進行了直觀的刻畫,并把相應的屬性約簡問題轉化為其誘導圖的極小頂點覆蓋問題。進一步地,利用圖論中的理論方法,設計了兩種啟發式的屬性約簡算法。實驗結果表明,所提出的約簡算法不僅可以選擇少量的主要特征,而且能保持甚至提高約簡數據的分類精度。尤其是所提出的GRF2算法,能高效的處理大規模的數據集。但是,GRF2所提取的特征個數仍然較多,因此,如何進一步去掉一些冗余的特征,這將是我們后續的主要工作之一。