基于改進魚群算法優化神經網絡的軸承故障診斷研究
張寧,魏秀業,郭小勇,徐晉宏
(1.中北大學 機械工程學院,太原 030051; 2.先進制造技術山西省重點實驗室,太原 030051)
滾動軸承在現代機械工業設備中必不可少,一旦軸承發生磨損、剝落或點蝕等故障,極易引起機械設備的故障。因此,有效地進行軸承的故障診斷,對保障機械設備的安全運行具有不可忽視的意義[1-2]。近年來,許多學者對軸承故障智能診斷進行了深入的研究,形成了一系列的方法,比如小波神經網絡[3]、遺傳算法優化神經網絡[4]、粒子群優化神經網絡等。但由于參數多且復雜,算法運行緩慢,而BP神經網絡有著易陷入局部極值的缺點。因此,嘗試用一種改進的魚群算法優化BP神經網絡,結合兩者的優勢,形成一套基于改進魚群算法優化神經網絡的軸承故障診斷方法。
1 改進的魚群算法
1.1 魚群算法
魚群算法[5]的流程如圖1所示,其從個體人工魚的局部尋優開始,自上而下地實現全局尋優。魚群算法具有全局收斂性好,收斂速度快,對初始值不敏感且對目標函數要求不高的特點,隨著多年的研究和探索,魚群算法的泛化能力越來越強,在許多實際工程問題的應用也越來越廣泛。

圖1 魚群算法的流程Fig.1 Flow of fish swarm algorithm
1.2 改進魚群算法的行為描述
1.2.1 自適應鄰域結構
傳統魚群算法中,由于視野和步長都是已知且設定好的定值,人工魚的鄰域結構較為局限,而基于自適應動態鄰域結構的魚群算法(Artificial Fish Swarm Algorithm Based on Adaptive Dynamic Neighborhood Structure,ADAFSA),即改進魚群算法中,人工魚的鄰域結構處于動態調整中,它們隨迭代次數的增加而變化,這就使算法的前期全局搜索能力和后期局部探索能力都得到增強,同時也提高了精度[6]。在第t次迭代時,人工魚i的鄰域為
Ni(t)=arg{max[sort(Di(t),′descend′),f(t)]},
(1)
Di(t)={di,j(t)|di,j(t)=‖Xi(t)-Xj(t)‖;
i≠j,j∈Nfish},
式中:Ni(t)為第t次迭代時人工魚i的所有鄰居魚集合;sort(A,′descend′)為對A進行排序;arg(B)為識別B的位置;Di(t)為人工魚i在第t次迭代時與其他人工魚的距離集合;Nfish為人工魚的初始規模;f(t)為第t次迭代時當前人工魚的鄰居魚個數;T為最大迭代次數;ceil(C)為C向正無窮方向取整數。
1.2.2 視野和步長
在改進魚群算法中,視野Lvisual和步長Lstep會自適應調整,在迭代過程中隨鄰域結構的變化而變化。
(2)
Lstep=aLvisual,
(3)
式中:a為視步系數,0 1.2.3 聚群行為 在進行到第t次迭代時,設人工魚的當前狀態為Xi,食物濃度為Yi,在其鄰域結構內共有f(t)條人工魚,找出中心位置的人工魚Xc,按下式執行聚群行為 (4) (5) 1.2.4 追尾行為 在第t次迭代時,設人工魚的當前狀態為Xi,食物濃度為Yi,尋找當前人工魚Xi鄰域結構內食物濃度最高的人工魚Xmax,若Ymax>Yi,按下式執行追尾,反之則進行覓食行為 (6) 1.2.5 覓食行為 當進行到第t次迭代時,設人工魚的當前狀態為Xi,食物濃度為Yi,在視野范圍內隨機找一條人工魚,設其狀態為Xk,食物濃度為Yk,若Yk>Yi,則人工魚Xi移動到Xk;若在設置的重復探索次數之后依然沒有找到大于Yi的食物濃度,則隨機移動一步。 BP神經網絡是一種具有非常強的復雜模式分類能力和多維函數映射能力的神經網絡模型[7],具有操作簡單,計算量小,并行性強等優點,但也存在網絡收斂速度慢,易陷入局部極小狀態且不保證其為誤差平面的最小值[8]等缺點。因此,需對其進行優化。 ADAFSA-BP的實質是利用ADAFAS的全局尋優能力,將BP神經網絡的初始閾值和權值調整到最優值附近,不僅能夠解決網絡振蕩的問題,而且可以較好地避免陷入局部極值。 將人工魚的當前狀態設為初始權值與閾值,人工魚的食物濃度設置為神經網絡訓練誤差的倒數,食物濃度越大就意味著誤差越小,這樣人工魚的尋優過程就是不斷調整閾值和權值的過程。其具體步驟如下: 1)BP神經網絡拓撲結構的設定,即BP神經網絡的層數和各層神經元的數目。 2)ADAFSA的參數設置,即初始化人工魚群的數目Nfish,最大迭代次數T,視步系數a,重復探索次數N。 3)將人工魚的狀態設為神經網絡的權值和閾值,神經網絡訓練誤差的倒數設為人工魚的食物濃度。 4)運行ADAFSA,結束后提取最優的人工魚狀態。 5)將提取的人工魚狀態賦予BP神經網絡,作為初始閾值和權值。 6)訓練BP神經網絡,并進行仿真預測。 神經網絡的拓撲結構設置為2-7-1,取8組樣本分別對ADAFSA-BP和BP網絡進行仿真。結果如圖2所示。 圖2 ADAFSA-BP和BP的仿真預測結果Fig.2 Simulation prediction results obtained by ADAFSA-BP and BP 從圖2可以看出,ADAFSA-BP的預測值與實際值基本相符,而BP神經網絡預測結果的各組之間都存在不同程度的偏差,準確率較低。說明ADAFSA-BP在理論上有較高的診斷率。 試驗軸承為6406型深溝球軸承(具體參數見表1),通過在內、外圈滾道上加工一個輕微凹痕(直徑0.54 mm,深度0.26 mm)模擬早期故障。設置采樣頻率為8 000 Hz,采樣點數為2 048,從JZQ250型減速器齒輪箱(圖3)中分別采集正常、外圈故障、內圈故障工況下的軸承振動信號,結果如圖4所示。 表1 試驗軸承的基本參數Tab.1 Basic parameters for test bearing 圖3 故障模擬試驗臺示意圖Fig.3 Diagram of fault simulation test rig 圖4 軸承不同運行狀態下的振動信號Fig.4 Vibration signals of bearing under different operating conditions 故障特征的提取對診斷的準確性有決定性的影響,因此提取出的特征必須能較好地體現各工況下齒輪箱的差異,也就是說故障特征要對工況的變化很敏感[9]。 針對實際故障軸承的振動信號具有周期性沖擊衰減的特點,采用基于粒子群優化的核主元分析特征提取方法:首先,根據試驗數據計算出所有時頻域特征參數,并算取各個特征值的均值,作為特征參數集;其次,利用粒子群算法優化徑向基核函數的參數;然后,通過核主元分析特征提取方法,根據主元對特征集貢獻率的大小,提取有效特征;最后,選取波形指標、峭度指標、裕度指標、偏態指標、頻譜重心、頻域方差、相關因子作為試驗的故障特征值[10]。將上述7個故障特征值進行歸一化處理,即 (7) 式中:xig為歸一化之后的特征值;xi為第i個特征值;xmax和xmin分別為xi的最大值和最小值。歸一化處理后神經網絡的訓練與測試樣本見表2。由于篇幅限制,每種工況下的訓練樣本只列出了2組,2組測試樣本則全部列出。 表2 齒輪箱軸承訓練樣本與測試樣本特征參量Tab.2 Characteristic parameters of training samples and test samples for gearbox bearing BP神經網絡的結構:神經網絡的拓撲結構設為7-12-3,隱含層和輸出層神經元的傳遞函數分別選用tansig和logsig,訓練函數則選用trainlm,訓練次數設為1 000,訓練目標設為0.000 1,學習速率設為0.05。 ADAFSA的參數設置:將人工魚的狀態設為BP神經網絡的初始權值和閾值,人工魚的食物濃度設為神經網絡訓練誤差的倒數,人工魚群的規模設為50,重復探索次數try-number設為50,最大迭代次數設為50,視步系數為0.1。 ADAFSA-BP的訓練誤差及隨迭代步數的收斂曲線如圖5所示。從圖中可以看出,算法在前15次迭代過程中速度較快,中期收斂速度緩慢,最后在第34次迭代時達到收斂。 圖5 ADAFSA-BP收斂曲線Fig.5 Convergence curve of ADAFSA-BP 為驗證ADAFSA-BP算法的高效性,選取遺傳算法優化BP神經網絡(GA-BP)和混合蛙跳算法優化BP神經網絡(SFLA-BP)與之作對比。選用相同的試驗數據和相關參數,對3種方法分別進行30次試驗,取神經網絡輸出值與理想值偏差的平均值作為綜合指標,選取一組測試結果進行對比,結果見表3。 表3 不同診斷方法的測試結果對比Tab.3 Comparison of test results obtained by different diagnostic methods 由表可知,SFLA-BP網絡模型診斷結果中第1組樣本的輸出與期望值偏差較大,數據0.476瀕臨限值,極易導致診斷錯誤;GA-BP網絡模型診斷結果中第3組、第4組樣本的輸出與期望值偏差較大;而ADAFSA-BP網絡模型中輸出值與理想值的整體吻合度相對較高。表中綜合指標顯示,ADAFSA-BP網絡模型偏差平均值小于GA-BP和SFLA-BP。綜上分析得知,ADAFSA-BP算法在軸承故障診斷中誤差相對較小,準確度相對較高。 針對齒輪箱軸承故障的診斷問題,提出了一種基于改進魚群算法優化神經網絡的軸承故障診斷方法,通過優化BP神經網絡的權值與閾值,提高網絡的收斂速度,且參數較少,容易實現,可以有效判斷軸承的故障類型。 在研究中發現,ADAFSA-BP算法的運行時間較長,一方面與改進的魚群算法中人工魚的維度高有關,另一方面與算法的終止條件有關。因此可以針對這一問題,進一步開展神經網絡結構優化方法的研究。2 改進魚群算法優化BP神經網絡
2.1 ADAFSA-BP網絡模型
2.2 算法驗證

3 ADAFSA-BP在軸承故障診斷中的應用
3.1 信號采集



3.2 選取故障特征值
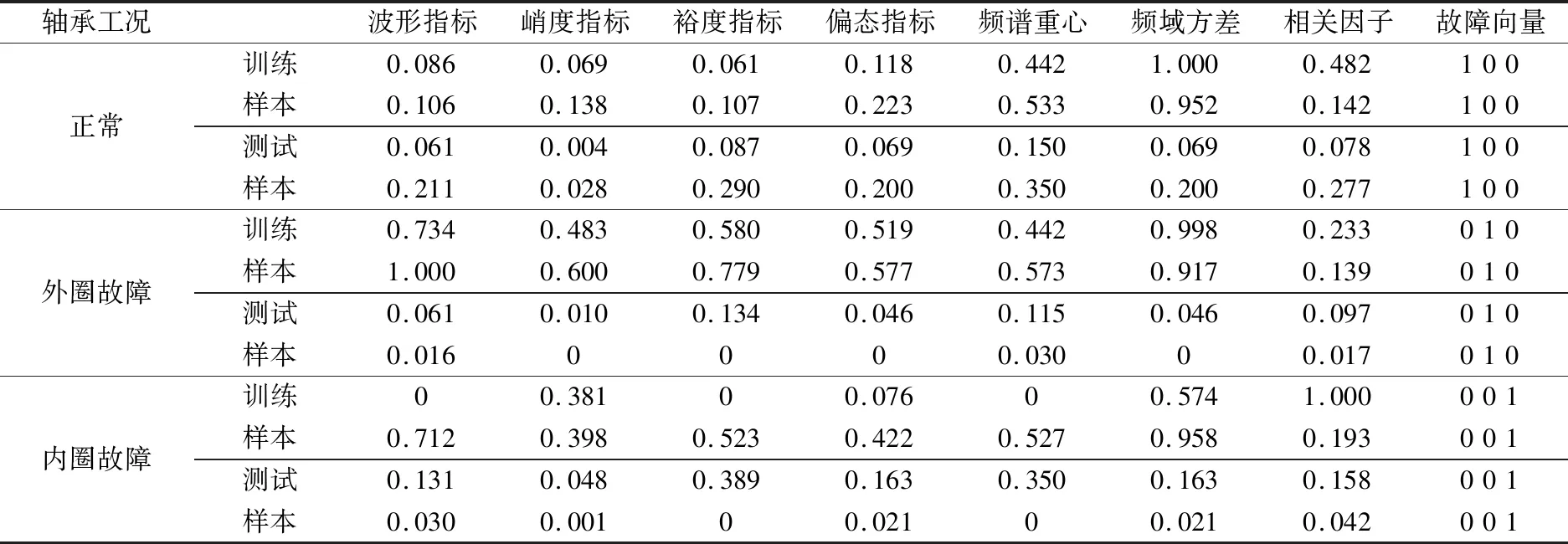
3.3 參數設置及診斷系統構建
3.4 仿真結果與分析


4 結束語

