回歸正交設計在車速再現不確定度評定中的應用

中汽研汽車檢驗中心(武漢)有限公司 楊文飛 李勰 王旭敏

道路交通事故司法鑒定實踐中的車速再現一般通過特定的模型進行計算，利用回歸正交設計方法對典型的車-人碰撞事故的車速再現模型進行不確定度分析，通過正交試驗設計、回歸分析以及參數取值范圍得到車速的不確定度，通過與不確定度評定基本方法的結果進行對比，兩者十分接近。通過極差分析表明車-人事故中人體與路面的摩擦系數μ對車速再現結果影響最大，這對實際司法鑒定中車速再現不確定參數的勘測和選取具有指導意義。最后通過一起典型車-人事故的車速再現，驗證了上述方法在司法鑒定實踐中應用的可行性和準確性。

近年來，隨著整個社會的法制、維權意識的增強和提高，對道路交通事故責任認定起重要作用的車輛行駛速度再現越來越受到事故各相關方的重視和關注。目前，道路交通事故中事故車輛行駛速度的再現方法主要包括基于事故形態、基于軟件模擬、基于車載記錄數據和基于視頻圖像等4種車速再現方法[1]，其中基于事故形態和視頻圖像的速度再現方法在司法鑒定實踐中應用廣泛，且都形成了國家標準[2,3]。根據具體事故中能夠提供的鑒案材料或勘驗資料，鑒定人員選擇合適的方法進行車速再現分析，有時也在同一個事故中利用多種方法計算的結果進行相互驗證。國家標準[2]給出了各種模型的計算公式和不同類別摩擦系數取值范圍，在實際事故勘查中獲取的制動印痕長度、變形量、拋距等參數大多時候是一個取值范圍。因此，通過所收集的參數計算得出車速再現的不確定度就能夠增加車速再現結果的科學性和可信度，并且在一定程度上可以排除主觀因素對結果的影響。許多學者已對不確定度基本評定方法[4]、蒙特卡洛評定方法[5-7]、上下界評定法、差分評定法以及響應表面評定法[8]做過研究，但多是針對給定軟件模擬初始值而進行研究。本文針對事故車速再現司法鑒定的具體實踐，把回歸正交設計方法應用于典型車-人事故車速再現結果的不確定度分析與計算中，所得車速再現結果與不確定度基本評定方法所得到的結果十分接近，從而論證了回歸正交設計方法的科學性和有效性。通過一個實際車-人碰撞事故案例，對回歸正交設計方法應用于車速再現司法鑒定實踐的可行性進行了驗證和說明。

回歸正交設計方法

為了利用正交試驗設計和回歸分析兩種方法的優勢，統計學者提出了回歸正交設計方法，通過這種方法不但能構建合理的試驗設計，而且只需較少的試驗次數就能得到有效的數學模型[9]。回歸正交設計可以在因素的試驗范圍（或稱取值區間）內選擇適當的試驗點，用較少的試驗建立一個擬合精度高、統計性質好的一次回歸方程，進而解決不確定度評定的問題。在車速不確定度評定的應用中，應用此方法可以計算得到非線性車速再現模型的一次回歸方程，從而解決非線性車速再現模型的不確定度評定分析問題。

1．試驗設計

被廣泛應用于各行各業的正交試驗設計的“整齊可比、均衡分散”的特點是通過正交表進行試驗設計來實現的[7]。回歸正交設計表可以通過正交表變換得到，即將二水平正交表中的“2”用“-1”代換。正交表L（27）經過變換后8得到的回歸正交設計表，其中的“1”表示因素的上水平，“-1”表示因素的下水平。回歸正交設計表中任一列編碼的和為零，任兩列編碼的乘積之和等于零，這表明通過正交表得到的回歸正交設計表同樣具有正交性。

2.試驗方案的確定

根據正交表L（27）的表頭設計表，可以進行相應

8的回歸正交設計表的表頭設計。在考察三個因素的情況下，各因素應分別放在第1、2和4列[9]，用相應參數的上、下水平值依次替換回歸正交設計表中的“1”和“-1”就可以得到最終的試驗方案。

3.回歸分析原理和步驟

回歸正交設計的總思想就是利用正交設計、回歸分析原理，建立試驗指標(y)與m個試驗因素x1，x2…，xm之間的回歸方程：

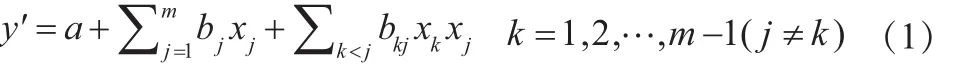
若不考慮因素間的交互作用，即式(1)中的交互項，則回歸方程為一次多元線性方程：

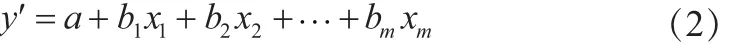
式中，x為各因素的輸入量，x=(x1，x2，…，xm)T；y′為試驗指標的輸出量；m為輸入變量個數；a,b,b1,b2,…，bm為回歸系數。

基于事故形態的車速重建再現本質上可以看作是一個由物理方程組組成的再現模型，其中用于計算車速的不確定參數是再現模型的輸入量，計算得到的車速是再現模型的輸出量。試驗方案確定后，就可以根據車速再現模型得到試驗結果，再通過回歸分析確定式(2)中的回歸系數，從而得到車速再現模型的一次回歸方程，最后利用不確定參數的取值范圍通過上下界法來確定車速再現結果的不確定度。

典型車-人碰撞事故車速再現不確定度分析

以文獻[4]中的典型車-人碰撞事故中車輛行駛速度再現模型為例，說明和驗證回歸正交設計方法應用于車速再現不確定度分析中的可行性和科學性。該車速再現模型是非線性的，計算公式為：

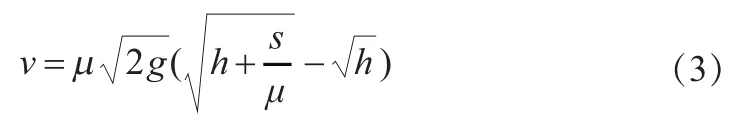
式中，h為人體的拋出高度；μ為人體與路面的摩擦系數；s為人體的拋出距離；g為重力加速度。參數h、μ和s在實際事故中的勘驗和選取過程中都會產生不確定性，因此確定這3個參數為此計算模型的不確定因素。根據文獻給出的數據，這三個不確定因素取值范圍分別為h=0.93±0.1m，μ=0.6±0.1和s=18.8±0.5m。根據前文的試驗方案設計進行試驗，得到的試驗結果如表1所示。

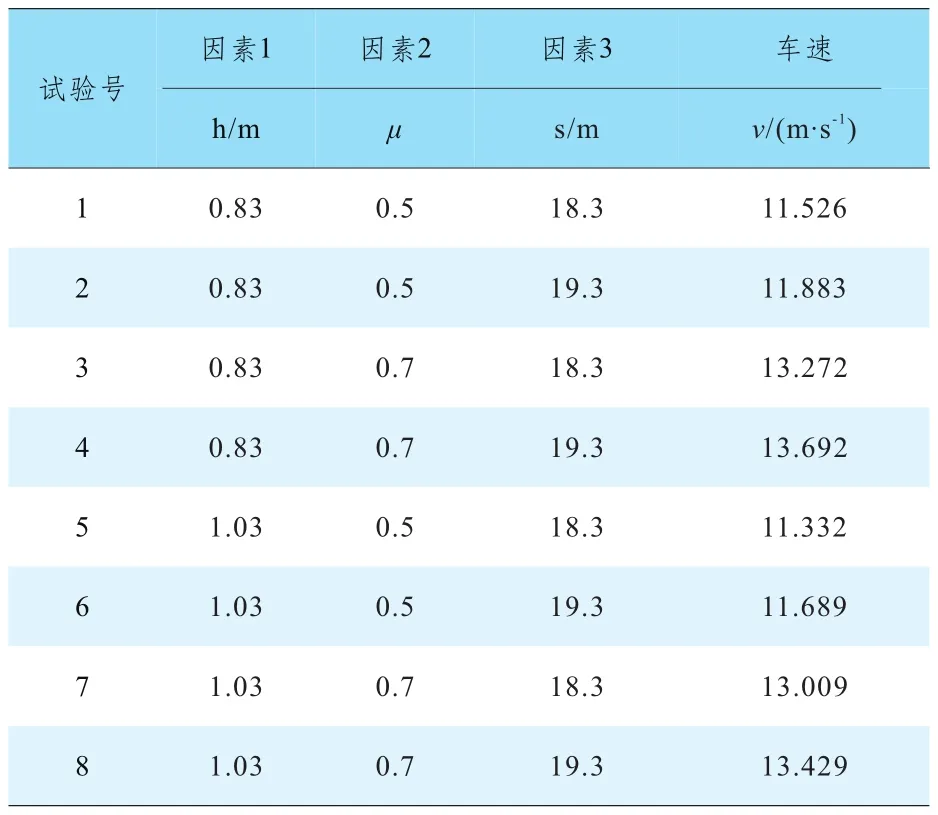
表1 回歸正交設計試驗方案和試驗結果

通過回歸分析，計算得到車速再現模型(3)的一次回歸方程為：

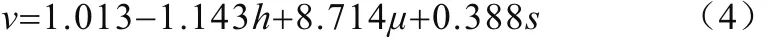
回歸分析的檢驗結果如表2所示。回歸方程(4)總體擬合優度（調整后的R2）為0.999，且通過了方差F檢驗，表明此回歸方程總體顯著；從回歸系數的檢驗來看，三個自變量因素回歸系數的p值均小于0.05，因此，三個自變量因素均對車速v有顯著影響，所以回歸方程(4)可以高度擬合典型車-人碰撞事故的車速再現模型(3)。

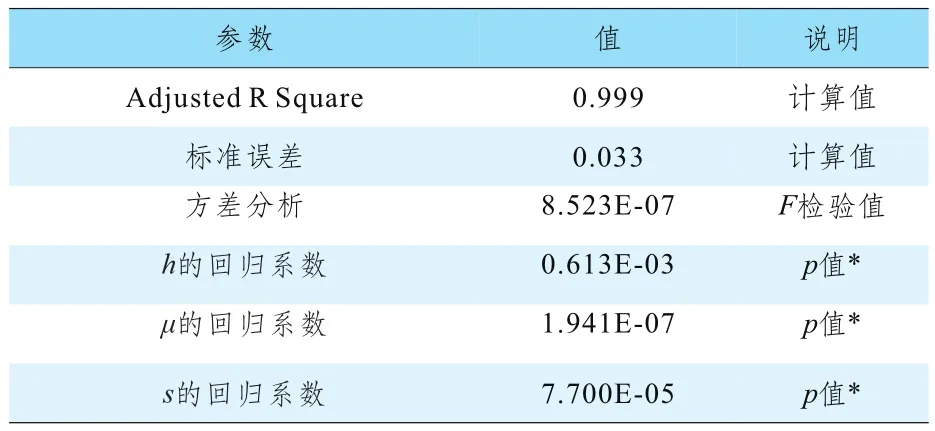
表2 回歸方(4)的統計檢驗

根據式(4)和不確定因素的取值范圍利用上下界法就可以計算得到車速再現結果的不確定度。為了驗證回歸正交設計方法的科學性和有效性，與文獻[4]中的不確定度評定基本方法計算所得結果進行比較，兩種方法的結果對比如表3所示。

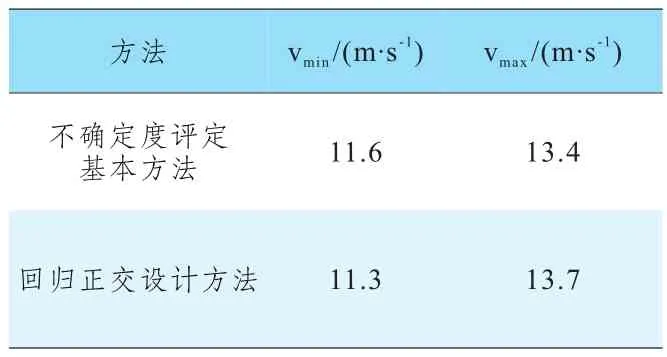
表3 不同方法不確定度評定結果的對比

從表3可以看出，兩種方法所得結果十分接近，各自上、下界值的偏差都在3%以內，從而有效地說明和驗證了回歸正交設計方法的科學性和有效性。

不確定因素對車速再現的影響

極差法能夠直觀、有效地處理和分析正交試驗的結果數據[10]。由上文可知，通過正交表得到的回歸正交設計表同樣具有正交性，因此能夠利用極差法對回歸正交設計試驗結果進行對比分析。由表1試驗結果計算得到各因素不同水平的極差如表4所示。表中Ij表示各因素4次下水平試驗值的加權和，IIj表示各因素4次上水平試驗值的加權和，Rj表示各因素不同水平加權和的極差。

表4 不確定因素的極差

由表4可知Ru>RS>Rh，即在典型車-人事故車速再現中，不確定因素對車速再現結果的影響由強到弱的順序為：人體與路面的摩擦系數μ、人體的拋出距離s、人體的拋出高度h。通過極差比較可知，人體與路面的摩擦系數μ對再現結果的影響遠大于人體的拋出距離s和人體的拋出高度h，因此在車-人碰撞事故車速再現的司法鑒定實踐中，應該更加注重人體與路面的摩擦系數μ的選取，進而提高車速再現結果的科學性與準確性，這對車速再現司法鑒定工作中不確定參數的勘驗和選取具有一定指導意義。

實際車-人碰撞事故車速再現

為了驗證回歸正交設計方法應用于車速再現司法鑒定實踐的可行性，選取一個實際的車-人碰撞事故說明上述方法在司法鑒定實踐中的應用。某日下午19時許，在某市一條主干道上，一位過馬路的行人被一輛水泥攪拌車撞倒。根據交警調查和事故現場圖得到行人拋距取值區間為[17.8，18.3]m；拋出高度取值區間為[0.95，1.05]m；人體與地面的摩擦因素取值區間為[0.55，0.65]。

利用前文所述方法計算得到得到式(3)的回歸方程為：

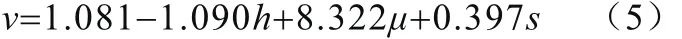
回歸方程(5)的總體擬合優度（調整后的R2）為0.999，且通過了方差F檢驗，因此回歸方程總體顯著，再利用不確定因素的取值區間通過上下界法計算得到此次車-人碰撞事故車速再現結果為[42，46]km/h。

另外根據行車記錄儀的視頻記錄計算的車速約為45 km/h，即通過回歸正交設計方法得到的車速不確定度涵蓋了45 km/h這一速度值。在視頻圖像足夠清晰，參考物容易確定的情況下，通過視頻圖像計算的車速是比較準確的[3]。因此，利用回歸正交設計方法計算的速度不確定度區間包含了相對準確的速度值45 km/h，說明此方法能夠應用于車速再現的有關司法鑒定實踐,特別是在許多案件由于現場條件缺乏視頻圖像等鑒案資料的情況下，更能顯示出此方法的優越性。

結語

本文采用回歸正交設計方法對典型的車-人碰撞事故車速再現結果的不確定度進行了研究，首先通過正交試驗設計和回歸分析得到典型的車-人碰撞事故車速再現模型的回歸方程，再結合不確定性因素的取值區間和上下界法計算得出了車速的不確定度區間，所得結果與不確定度基本評定方法所得結果十分接近，驗證了回歸正交設計方法的科學性和有效性。接著通過極差分析得到，相比于人體的拋出距離s和人體的拋出高度h，人體與路面的摩擦系數μ對車-人碰撞事故車速再現結果影響更大，這對司法鑒定實踐中的車速再現分析具有一定的指導意義。最后，通過一起真實道路的車-人碰撞事故驗證了回歸正交設計方法應用于車速再現司法鑒定實踐的可行性和準確性。