軟巖非定常分數階蠕變模型研究
王紅娟,鄧輝, 唐梓豪,李萬才
(成都理工大學 地質災害防治與地質環境保護國家重點實驗室,四川成都610059)
流變學的研究較為復雜,其中巖土體蠕變是流變的重要研究內容之一。蠕變被定義為在恒應力作用下應變與時間的關系。軟弱工程巖體的蠕變特性對工程的影響有著很重要的影響[1],加速蠕變階段的描述既是重點,又是難點。
現如今,有大量的蠕變模型被提出用以描述巖石蠕變的變形特征。按照構建模型的方法,可分為元件和經驗模型。趙寶云[2]等對砂巖短時三軸蠕變模型的黏性元件進行了非線性改進,與Kelvin模型串聯,得到了一種新的黏彈塑性蠕變模型,該模型可正確表征蠕變4個階段的特征。最后,基于BFUS非線性優化算法對該模型參數進行了識別,同時將模型擬合曲線與改進西原模型曲線進行了比較分析,驗證了非線性黏彈塑性蠕變模型的正確性;郭佳奇[3]等用FC元件取代整數階微積分Kelvin-Voigt流變模型中的牛頓體元件,形成了基于分數階微積分的蠕變模型,該模型在保證了擬合精度的情況下減少了模型參數;陳家瑞[4]等在分數階微積分理論的基礎上,基于三參量流變模型,提出了一個新的流變模型,結合數學軟件1stOpt擬合參數,最終得到的模型能較好地描述破碎泥巖的流變規律;楊文東[5]等提出了由瞬彈性Hooke體,黏彈塑性村山體和非線性黏彈塑性體串聯而成的巖石非線性黏彈塑性流變模型,該流變模型可以描述巖石流變的減速、等速特別是加速蠕變階段,且通過反演,該模型的可靠性也得到證實;張明[6]等就錦屏一級水電站的大理巖進行流變模型的選擇,提出了Hooke-Kelvin模型,該模型較Burgers模型更適合表達大理巖的蠕變特征;徐衛亞[7]等提出了由黏彈塑性體和五元件線性黏彈性模型串聯的河海模型,該模型能較好地反應巖石加速流變的性質。以上大多只通過與某一種巖石的試驗數據進行擬合來驗證模型正確性,不具有廣泛代表性。
綜合以上考慮,本文基于分數階微積分,提出了一種能正確表征加速蠕變階段的蠕變方程,以西原模型為基礎,引入了加速流變起始時間點[8],采用軟體元件表示非線性階段,提出了一種參數可變的非線性黏彈性蠕變模型,給出了該模型的本構方程。并使用不同類型巖石在不同圍壓下的蠕變試驗數據對該模型進行了驗證,結果表明,試驗數據與預測曲線都能較好地吻合,驗證了模型的正確性。
1 分數階微積分定義簡介
本文提出的蠕變模型需要借助于分數階微積分理論,故對分數階微積分做如下簡單介紹。
分數階微積分有多種不同定義。在巖土工程學科中,Riemann-Liouville定義應用最廣。以下對R-L定義進行簡單介紹[9]。對于函數f(t)的β階積分定義為
(1)
式中,d為微分算子。分數階微分則定義為:
(2)
式中,β>0,且n-1<β≤n(n為正整數)。
Γ(β)為Gamma函數,其定義為:
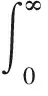
(3)
2 基于分數階微積分建立的軟體元件
理想彈性體的應力應變關系滿足Hook定律,即σ(t)~ε(t),其蠕變形式表達為:
(4)
式中σ——常應力;E——彈性模量[10]。
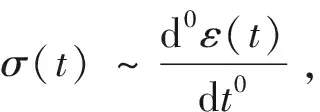
(5)
式中η——黏性系數。

(6)
式中η——黏性系數;β——求導階數。
當應力為常數時,即σ保持不變。元件將描述流變行為的蠕變,對式(6)兩邊進行分數階積分,根據分數階R-L積分定義,可得:
(7)
當β=0或β=1時,即Γ(β+1)=Γ(1)或Γ(β+1)=Γ(2) 時,式(7)退化為Hook體和Newton 體。
3 分數階流變模型的建立
3.1 線性黏彈性流變模型
為得到一個應用范圍廣、適用性強且能更大程度模擬巖石蠕變過程的模型,本文建立了一個由彈簧體、開爾文體和一個可反應加速流變起始時間的黏塑性元件串聯組成的蠕變模型,見圖1。
在線性流變模型中,當σ<σs時,即i和ii共同作用時[11],應變有如下關系:
εi,ii=εe+εve
(8)
式中εe——胡克體中彈簧的彈性應變;εve——黏彈性應變;εi,ii——瞬時蠕變和穩態蠕變的總和。Hook體中,應力應變有如下關系:
σ=EH·εe
(9)
式中,EH為胡克體中彈簧的彈性模量。Newton/Kelvin體中,應力應變關系如下:
(10)
εe1為開爾文體中彈簧彈性應變,γ意義如上,由并聯模型性質可知:
εe1=εve=εii
(11)
所以得到:
(12)
即
(13)
對式(13)進行Laplace變換得:
(14)
式中,E(s)為復變量s的函數,解得:
(15)
對式(15)進行拉普拉斯逆變換得:
εve(t)=
(16)
3.2 非線性黏塑性元件
李良泉[8]假定破壞荷載和破壞時間、破壞荷載和加速流變歷時存在一定的關系,可用指數形式來表示為:
(17)
式中t——破壞時間;σ0——巖石瞬時強度;σ∞——長期強度;Δt——加速流變歷時;α和β均為常系數,則可得巖石加速流變的起始時間為:
(18)
徐衛亞[7]就綠片巖三軸流變試驗曲線,提出了一個可反映加速流變特性的非線性黏塑性體。本文引用其形式,同時引入一個新的參數Δt,可得非線性階段蠕變方程為
(19)
即:
(20)
3.3 考慮參數可變的流變模型
現有的蠕變模型大多是由元件模型經過串并聯組合而成,且力學參數很多為常參數,但在實際情況下,如黏滯系數和彈性模量等的取值都是時間的函數。丁志坤[12]根據試驗,提出了EH是定常而EK是時間t的函數,并給出了EK的表達式為:
EK(t)=p1+p2ep3t
(21)
式中,p1、p2、p3為常參數,本文考慮了彈性模量為非定常的情況,綜合三部分應變,可得到巖石非線性黏彈塑性本構模型,該模型的本構方程為:
ε(t)=
(22)
4 模型驗證
本文所提出的五元件蠕變模型,結合黃海峰等[13-15]對不同種類巖石的蠕變試驗數據對模型進行擬合。紅砂的應力大小和長期強度分別為55、23.56 MPa,巖鹽的應力大小和長期強度分別為45、37.8 MPa,泥巖的應力大小和長期強度分別為40、36.21 MPa,由于所施加應力水平均大于長期強度,故需考慮加速階段。此時待擬合參數為11個,這是由于本文考慮了變參數[15]的影響,雖然擬合參數較多,但也可通過擬合工具快速獲取。本文利用數學軟件1stOpt對式(22)中的參數進行擬合,所得結果見表1。經計算得知:紅砂巖、鹽巖和泥巖的相關系數R2的值分別為0.97、0.96和0.99。試驗值與擬合曲線對比見圖2,可見試驗值和擬合曲線符合很好,這是由于采用了分數階進行建模[17-19]。表1和圖2僅僅展示了圍壓100 MPa下的擬合效果,為了進一步檢驗該模型,采用200 MPa下的紅砂巖蠕變數據模擬,結果見圖3。可見,新模型能夠較好地反映軟巖的蠕變特性。

表1 非線性蠕變模型參數
通過對比曲線可以發現,對于3種不同的巖石來說,瞬時蠕變階段和穩態階段都能較好地吻合,非線性階段的試驗曲線也能和預測曲線大致重合,證明了該模型的適用性和正確性。
5 結論
本文依據元件模型,在元件本構方程基礎上引入非定常參數,使模型能更準確描述巖石蠕變全過程,通過紅砂巖、巖鹽以及泥巖的蠕變試驗數據對該模型的驗證,得到以下結論。
a) 通過對紅砂巖,巖鹽以及泥巖試驗數據的擬合,發現該模型能較好地擬合巖石流變過程,加速階段同樣吻合,具有合理性,同時也證明了模型的適用性。
b) 所建模型能較好地模擬軟巖的蠕變全過程,便于使用。在今后的研究中,將考慮把模型嵌入數值模擬軟件之中,以期將其很好地應用于工程實際之中。

