閘孔自由出流流量系數公式的改進與應用
----以槐店閘為例

秦晨光，毛豪林，王繼華，竇 明

(1.鄭州大學水利與環境學院，鄭州 450001；2.河南省鄭州水文水資源勘測局，鄭州 450000；3．河南省地質環境監測院，鄭州 450000)

0 引 言

近年來，隨著經濟社會的發展需要，閘壩工程在防洪、發電、灌溉、水運等方面發揮了越來越重要的作用。然而，閘壩建設人為改變了河流天然徑流過程，其實際流量、水位均發生了顯著變化。對于大多數中低水頭閘壩，泄流的特點是水頭不大，水力因素變化范圍大，閘門開啟調度過程中，能形成由急流到緩流的多變流態，對下游河床的沖刷防護不利，如若閘門運行時由于操作或人為因素形成多孔大開度時，將會對下游河床造成更劇烈的沖刷[1]。如果閘門泄流調度合理，就能減少消能防沖問題。因此，選擇一個合適的過閘流量計算公式、加強對閘壩工程的科學調度，不僅能有效減少洪災和旱災造成的損失，還能改善水環境、修復生態系統，對于調度工作的開展具有重要指導意義。許多學者針對閘孔出流做了很多相關的研究， 比如通過分析自由出流和淹沒出流兩種情況下的過閘水流流動特征，使用不同的方法預測流量系數，通過兩種模型的建立，提出相應的流量系數方程或者改進方程(I P Martynov[2])。在這一領域中，Henry[3]作為開創者，在對正常水閘出流特性進行研究后，在自由和淹沒流動條件下給出了相應的流量系數圖和系數公式，他的這項研究被后來的Rajaratnam 和 Subramanya[4]所證實，并在Henry研究的基礎上，提出了新的流量系數公式。隨著對流量系數研究的增多，越來越多的學者開始考慮其他因素對出流計算的影響，Prabhata K. Swamee[5]認為閘門流量系數是一個涉及幾何和水力參數的函數。通過數學計算獲得了高精度的淹沒和自由出流的流量系數方程，并給出了適用條件。A. Hussain[6]在對灌溉渠道圓孔出流進行研究時，將圓孔直徑和流體重力和慣性力考慮在內，提出了含有弗魯德數和圓孔尺寸的流量系數方程。Masoud Ghodsian[7]在對側閘門進行研究時，也得出了相似的結論，認為在亞臨界水流時弗魯德數會對流量系數產生一定影響。除了重力，流體的黏性力和表面張力也會對出流造成影響，A. Roth[8]通過實驗證實了這一點，并將雷諾數考慮到公式中，應用最廣泛的方法是回歸分析(邱靜[9]，葉云濤[10]，向華琦[11])，獲得較高精度公式的同時，又能解決一些實際問題。

1 研究方法

1.1 傳統流量系數經驗公式介紹

近年來，國外學者多側重于對收縮系數和淹沒系數的研究，但也不乏一些關于流量系數的研究。比如I. P. Martynov[2]在對溢洪道平板閘門出流進行研究時，將相對閘門開度作為自變量，得到流量系數關系式。對于閘孔出流流量系數的研究，國內外學者總結出了很多經驗公式，如表1所示。

表1 過閘流量系數公式總結

表示形式上，中國學者習慣把流量系數、閘門開度、閘前水頭分別用μ，e,和H0表示，歐美學者則用Cd，w和y0表示。在自變量的選取上，最為普遍的是尋找閘門相對開度和流量系數之間的函數關系。其中，閘門實際開度和閘前水頭是影響流量系數模擬精度的重要因素。

當為平板閘門時，一般認為e/H≤0.65時為閘孔出流，e/H≥0.65時為堰流。閘孔出流計算公式為：

式中：μ為流量系數；b為閘孔寬度；e為閘門開度；H0為閘前水深。

在表1提到的過閘流量系數公式中，有復合函數、冪函數、指數函數、一次函數、三次多項式5種形式，考慮到所研究對象為平原水閘，過流情況較為簡單，擬采用對數函數替換復合函數進行研究，五種公式的通用表達式如表2。

表2 5種公式通用表達式

1.2 過閘流量公式改進思路

針對以上提出的五種過閘流量計算公式，采用最小二乘法來率定各個公式的參數，并采用最大絕對誤差、相對誤差、變差系數3個指標分析各個公式的精度。再對5種公式計算結果進行驗證時，采用相關系數(r)、相對誤差(re)、納西效率指數(NSEC)三個指標來分析各公式計算值的精度。

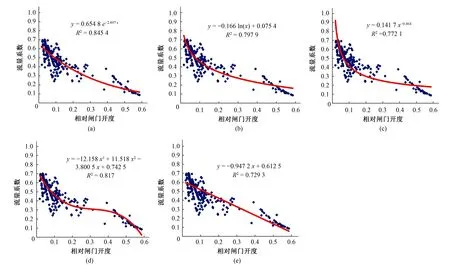
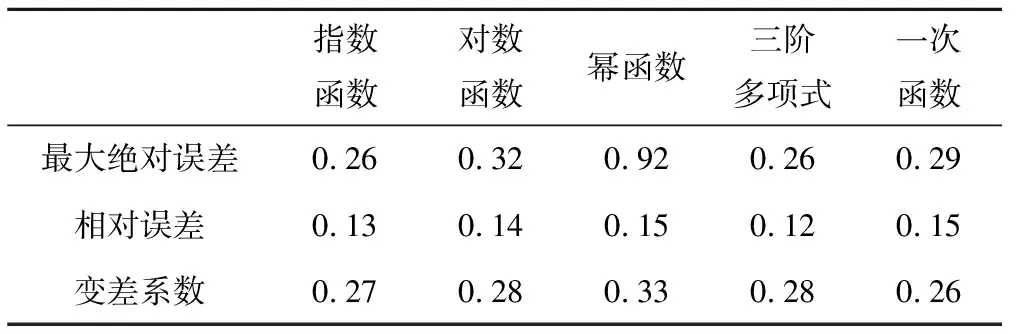
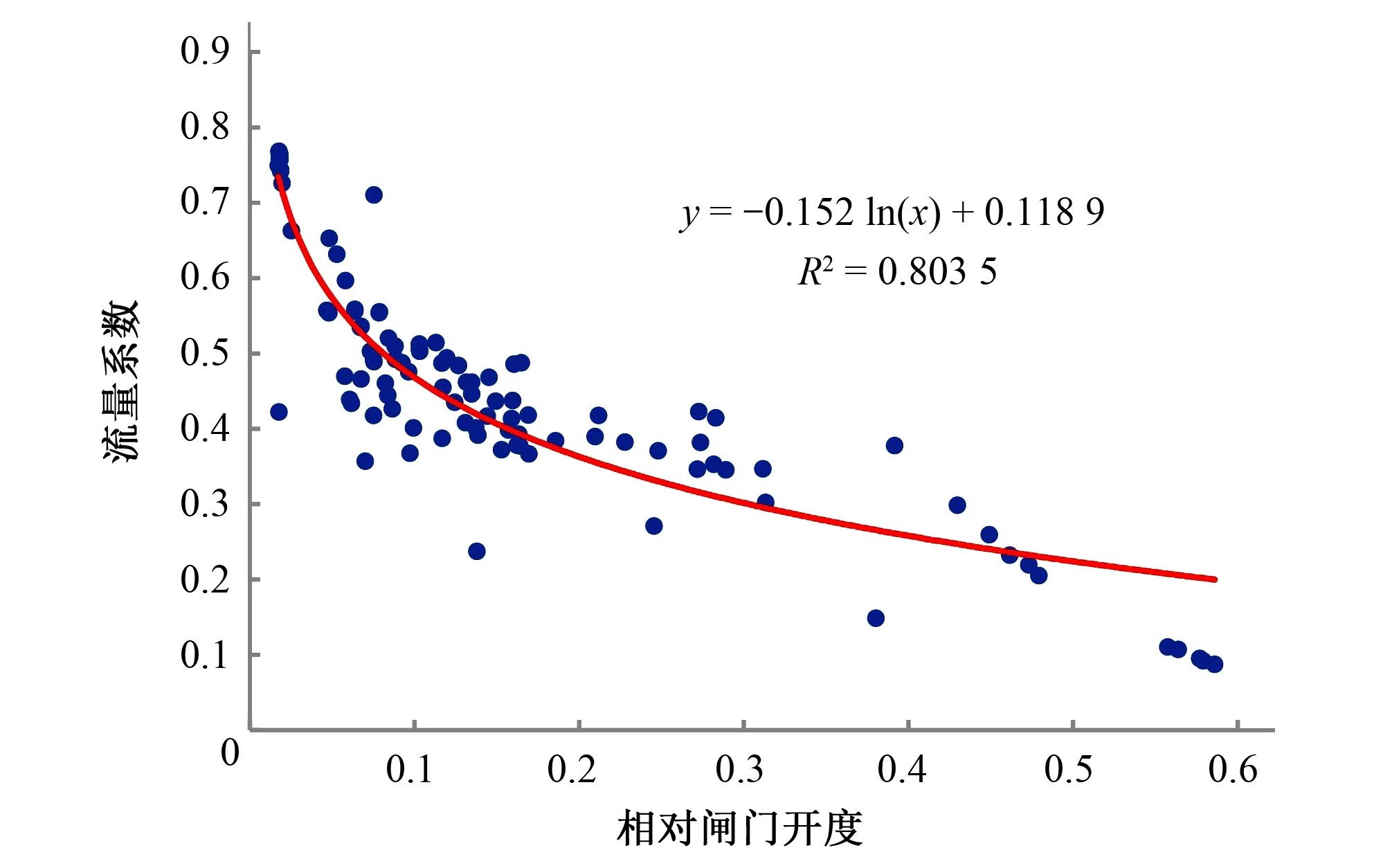
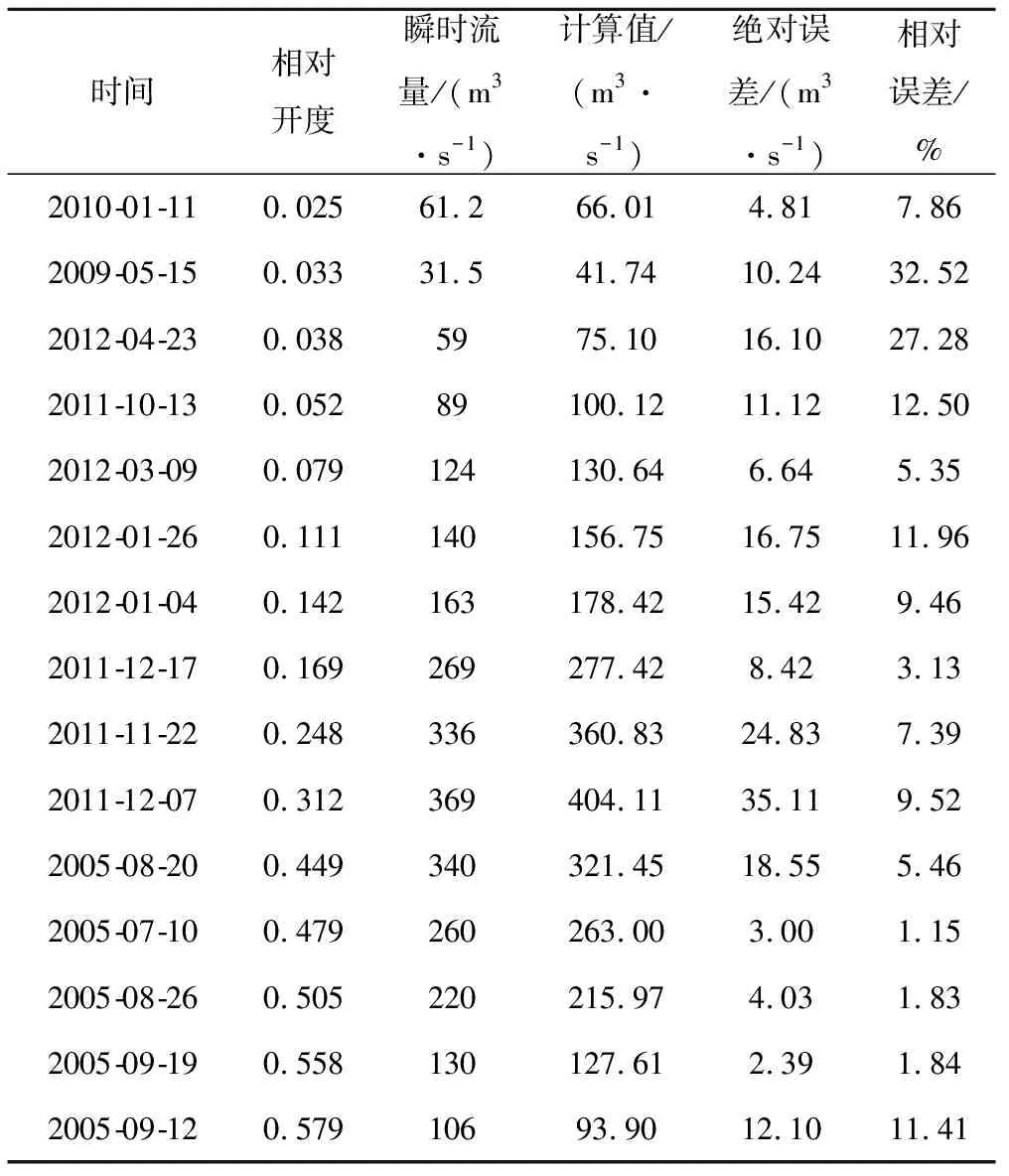
評判標準[17]如下：①當r≤1和NSEC≤1，re>0.15或<-0.15，模型預測結果較差。②當r=1和NSEC=1，re=0時，模擬效果最佳。③當r>0.6，NSEC>0.5， -0.15

通過對驗證期的精度分析，篩選出最適合槐店閘的流量系數公式，繼而采用最小二乘法對驗證期數據進行回歸分析，通過使誤差的平方和最小來尋求最佳匹配函數。模型函數確定為y=a+bt，令t=lnx，對數函數模型轉化為線性函數的擬合，y=a+bt，令：

求使F(a,b)有最小值的a和b的值。

得到正規方程組：

解得a和b的值，得到改進的流量系數公式。

針對改進前后的對數函數公式的擬合效果，我們進行了對比分析，并結合率定期和驗證期的流量系數散點圖，發現改進的對數函數只在相對開度區間處于0.08～0.42時精度得以提高，同時當相對開度在0.42～0.60時，流量系數與相對開度更趨于線性關系。綜上，決定采用分段函數形式表示流量系數與相對開度的關系。

2 應用研究

本文研究對象槐店閘位于河南省周口市沈丘縣槐店鎮，主要由淺孔閘、深孔閘、船閘三部分組成，淺孔閘長期保持小流量下泄，深孔閘只在洪水期供泄洪使用，船閘為正常通航使用。淺孔閘的設計流量為3 200 m3/s，水位40.88 m。淺孔閘共18孔，單孔凈寬6m，閘身總寬140.7 m，堰頂高程36 m，堰高1 m，安裝預應力鋼筋混凝土平板門，分上、下扉，配備2×22.5 t啟閉機9臺，每臺起閉2孔。深孔閘5孔，單孔凈寬10 m，閘身總寬60 m。正常蓄水量為3 000～3 700 億m3，最大蓄水量為4 500 億m3。正常灌溉水位38.50～39.50 m，最高灌溉水位40.00 m。

2.1 傳統過閘流量計算方法的驗證

通過對槐店閘2005-2012年的實測數據和泄流情況進行分析，此水閘屬于曲線型底坎，曲線型坎上的閘孔出流也分自由出流和淹沒出流兩種情況。在實際應用中，由于下游水位過高而使閘孔形成淹沒出流的情況十分少見，在觀測數據中也并未發現。因此本文只討論自由出流情況，選擇穩定的淺孔閘出流數據進行試驗，所選數據過閘流量與閘門開度隨時間變化的關系圖見圖1。

圖1 過閘流量與閘門開度隨時間變化關系圖

本文從水閘管理所收集了近7年(2005-2012年)的調度資料，包含上下游水位、閘前水頭、閘孔水深、閘孔流量和水位、閘門開啟度和個數等監測數據，從中選擇數據完整連續且前后沒有發生較大突變的數據用于實驗分析。其中，選擇2005-2010年的366組數據用于參數率定，2010-2012年的104組數據用于驗證模型。率定期5種擬合結果見圖2。

圖2 率定期5種方程擬合效果

由圖2可知，當閘門相對開度在0.02～0.30之間時，數據較為集中，這和采集數據時水閘常年保持小流量下泄較為吻合，當開度較大時，流量系數和相對開度的線性關系良好。在擬合得到的5種不同形式的關系式中，指數形式的相關性最好，一次函數雖然相關性最低，但在大開度時擬合效果較好。考慮到小開度時流體的黏性力，閘墩的側向收縮作用，在這一區間數據較多且較集中等因素，誤差多集中在這一部分。整體來看，一次函數的最大誤差較大，且對小開度擬合效果較差。

選用另外的104組數據對這5種公式進行驗證。驗證結果如圖3所示。

圖3 5種公式驗證結果

如圖4所示，當相對開度在0～0.10之間時，對數函數擬合效果相對較好，冪函數和一次函數誤差較大。當相對開度在0.10～0.35之間時，指數函數、對數函數、三階多項式與實測值較為接近，一次函數和冪函數誤差較大。當相對開度大于0.40時，對數函數和一次函數的擬合效果較好。總的來看，誤差較大的點多集中在大開度和小開度，大多數點的相對誤差則在較小范圍內變化。

結合表2給出的5種函數通用表達式，對率定期的數據進行擬合得到指數函數、對數函數、冪函數、三階多項式、一次函數五種形式的流量系數公式，計算各個公式最大絕對誤差、相對誤差、變差系數進行對比，如表3所示。

由表3可知，冪函數最大絕對誤差為0.92，遠高于其余4種公式，其次為對數函數和一次函數，三階多項式最大誤差最小，為0.26。冪函數最大誤差較大主要是因為當閘門開度較大時，擬合效果不理想導致。相對誤差最大的為冪函數，為0.15，一次函數相對誤差為0.15，雖然二者值相等，但擬合效果相差較大，一次函數在相對閘門開度大于0.4時，擬合效果較為理想，當相對開度處于0.01～0.20時，冪函數擬合效果較好。指數函數和對數函數相對誤差比較接近，三階多項式相對誤差最小。從變差系數上來看，冪函數變差系數最高，為0.325。擬合效果變化較大，指數函數、對數函數、三階多項式、一次函數的離散程度較為接近。

表3 率定期5種公式模擬流量系數對比

為了更好的比較5種公式在槐店閘的適用性，對于驗證期的數據采用相關系數(r)、相對誤差(re)、納西效率指數(NSEC)分析各公式計算值的精度。

計算結果如表4所示。

表4 5種公式驗證結果對比

由表4可知，對數函數的相關系數最大，為0.89，冪函數和指數函數其次，一次函數的相關性最差。就相對誤差來說，三階多項式最大，為0.06，指數函數和對數函數較為接近，分別為0.05、0.04。由圖2可知，當相對開度在0.02～0.27之間時，一次函數計算值要高于實測值，其余四種函數均低于實測值，其中，冪函數計算值遠低于實測值，當開度逐漸變大，一次函數計算值變化趨勢同實測值變化趨勢接近，指數函數和對數函數在整個變化區間都較為穩定，從納西效率系數上來看，對數函數最大，為0.76，指數函數其次，冪函數、一次函數、三階多項式都未超過0.60。

綜上所述，對數函數公式計算過閘流量時誤差較小，擬合效果較好，故選取對數函數公式進行改進，以便提高精度。

2.2 改進過閘流量計算公式的擬合效果對比

采用最小二乘法原理，對驗證期的數據進行曲線擬合，得到改進的對數函數公式 。

改進公式擬合效果如圖4所示。

圖4 改進公式擬合效果

由圖4可知，當閘門相對開度處于0.01～0.60之間時，改進的對數函數公式在整體上相對誤差減小，當e/H在0.42～0.60之間時，閘門相對開度和流量系數呈現良好的線性關系。對所有實測數據中閘門相對開度大于0.42的34組數據進行單獨觀察，同樣發現線性良好。并對其進行擬合，效果圖見圖5。

圖5 大開度數據擬合

由圖5可知，除了個別數據點偏差較大外，大多數點的擬合效果都較為理想，當閘門相對開度在0.5左右時有兩個點的偏差較大，可能與監測時過閘流量變化較大有關。綜上所述，決定采用分段函數形式來表達過閘流量系數公式，公式如下：

此公式考慮了閘門相對開度在0.01～0.60的自由出流區間內的所有出流情況，槐店閘常年保持小流量下泄，當0.01≤e/H≤0.08，由于數據較為集中，率定期的大量數據擬合所得對數函數模擬精度高于改進的對數函數；當0.08≤e/H≤0.42，驗證期數據減少，改進的對數函數較少受到小流量數據影響，因而擬合精度較高，在此區間采用改進對數函數；當0.42≤e/H≤0.60，泄流量較大，不容易受到其他因素干擾，此時閘門開度與流量系數的線性關系更加顯著，因而采用線性函數表達此區間流量系數關系式。

為了驗證上述流量系數公式的模擬精度，從2005-2012年的實際觀測數據中隨機抽取15組數據，且相鄰兩組相對開度差值不大，使數據均勻分布。并結合過閘流量計算公式進行計算，結果如表5所示。

表5 分段函數計算值與實測值對比

由表5可知，在所限定的公式適用范圍內， 計算值與實測值均較為接近，絕對誤差大大減小。當0.01≤e/H≤0.08范圍內時，絕對誤差平均保持在10 m3/s左右，由于閘門開度較小，實測流量值較小，平均相對誤差在17%左右，當0.08≤e/H≤0.60時，絕對誤差最大時為35.11 m3/s，相對實測值369 m3/s誤差不大，在此范圍內，平均相對誤差低于10%，證明公式模擬效果良好。

3 結 語

結合淮河流域上槐店閘的實測數據，擬合得到指數函數、對數函數、冪函數、一次函數、三階多項式5種不同形式的過閘流量計算公式，并探討了每種公式的精確性，發現對數函數適用性較好。為進一步提高模擬精度，在原有對數函數公式基礎上對其改進。對實測數據進行仔細觀察發現當相對開度大于0.42時，相對閘門開度與流量系數線性良好，于是對此區間數據進行單獨擬合得到一次函數公式，綜上采用分段函數形式表達流量系數并代入實測數據對比，平均相對誤差降至10%以下，誤差減小明顯。

上述分段函數在槐店閘上表現出了更好的適應性，提高了模擬結果的精度，對于指導今后的調度工作有一定借鑒作用。但是由于研究對象僅僅基于槐店閘，本文研究所得分段函數公式并不適用于閘底坎為寬頂堰以及遠大于槐店閘泄流量的曲頂堰自由出流計算，對于閘門技術參數和水力條件類似于槐店閘的水利工程，此公式具有一定的借鑒和參考價值。