基于災變因子的量子遺傳算法研究?

張秋艷 王默玉 申曉留 武書舟 閆麗娜 曹柳青

（華北電力大學控制與計算機工程學院 北京 102206）

1 引言

在現實生活中，許多優化問題要求人們不僅要計算出其極值，還要得出其最優值。這類問題對傳統的算法造成的嚴峻的挑戰。在這種情況下，越來越多的群智能算法相繼的提出，遺傳算法是由美國密歇根大學的John Holland 教授和他的同事與學生最早開始研究和應用的。是一種借鑒生物界自然選擇和進化機制發展起來的高度并行、隨機、自適應搜索算法［1］。簡而言之，它使用了群體搜索技術，將種群（population）代表一組問題解，通過對當前種群施加選擇（selection）、交叉（crossover）和變異（mutation）等一系列遺傳算子（operator），從而產生新一代種群，并逐步使種群進化到包含近似最優解的狀態。由于其思想簡單、易于實現以及表現出來的健壯性，遺傳算法贏得了許多應用領域，特別是近年來在問題求解、優化和搜索、機器學習、智能控制、模式識別和人工生命等領域取得了許多令人鼓舞的成就。

2000 年，K.H，HAN 等在文獻中提出在遺傳編碼過程中加入量子的態矢量表達，首次創造性地提出了量子遺傳算法并在量子旋轉門的基礎上，實現了個體染色體的基因調整策略，大大提高了量子遺傳算法在量子計算機上運行的可能性。

2 量子遺傳算法理論與方法

在量子遺傳算法中，最重要的是量子編碼和量子門的引入。量子編碼是將染色體用量子的態矢量表示，使一條染色體表達為多個態的疊加，從而增加了種群多樣性，使算法能夠在較小的種群規模下求得最優解；而量子門的引入使算法具備了開發能力和探索能力，可以保證算法收斂［14～15］。目前，量子遺傳算法被應用到了多個領域，如電網規劃以及圖像處理等［2～4，13］。

2.1 量子編碼

在量子遺傳算法中，使用了一種新穎的基于量子比特的編碼方式，即用一對復數定義一個量子比特位，一個具有m 個量子比特位的系統可以描述為

其中，|αi|2+ |βi|2=1(i=1,2,…,m)。

量子比特位可以同時處于兩個量子態的疊加態 φ =α0 +β1 中，如:其中 0 和 1 分別表示自旋向下態和自旋向上態，φ 為一種量子態的表示，式中 α 和 β 為復數，表示量子位狀態的概率幅，| α|2i可看成量子處于自旋向下態的概率，| β|2可看成量i子處于自旋向上態的概率。

若有一個具有三個量子比特位的量子編碼:

則該量子編碼可以轉換為如下形式的二進制編碼。

即該量子編碼轉換為|000|、|001|、|100|、|101| 的概率分別為1/8、3/8、1/8、3/8。所以，該量子編碼具有四個二進制編碼的信息，顯然這種編碼方式能夠使種群擁有更好的多樣性，且隨著 |α|2、| β|2ii趨于0 或1，染色體將收斂于一個單一態。因此，與遺傳算法相比，量子遺傳算法在較小的種群規模下就可以得到最優解。

2.2 量子門

量子門作為完成進化的操作機構，可以根據具體情況進行選取，目前已有多種量子門，按照量子遺傳算法的特點，選擇量子旋轉門作為執行機構較為合適。

通過量子門變換矩陣可以實現種群的更新實際上量子門變換矩陣是一個可逆的歸一化矩陣，即需要滿足UU*=U*U=1。

常用的量子旋轉門為

其中[α ,β]T為染色體中的第i 個量子位，θ 旋轉iii角。

2.3 量子遺傳算法流程

量子遺傳算法首先取規模為N 的種群進行初始化，一般情況，種群中全部染色體的所有基因都被初始化為(1/ 2,1/ 2)；然后對初始種群每個個體實時一次測量，得到一個狀態P（t），然后對這一組解進行適應度評估，記錄下最佳最適應度個體作為下一步演化的目標值［5］。并實時記錄最佳個體及其適應度值。具體算法基本步驟如下:

t=0

對Q（t）初始化

通過觀察Q（t）的狀態確定P（t）

評價P（t）保存中的最優個體

如果不滿足終止條件

Begin

t=t+1 ；

通過觀察Q（t）的狀態確定P（t）

評價P（t）保存中的最優個體

用量子門U（t）更新Q（t）

保存P（t）中的最佳個體

直至滿足終止條件

圖1 量子遺傳算法流程

2.4 災變因子

為了進一步提高全局搜索性能，引入“災變”概念到遺傳算法中。在生物進化過程中，“災變”就是外部環境的巨大變化，如冰河期、森林大火、大地震和瘟疫等，是對絕大多數生物的滅頂之災，造成了大量物種或者個體的滅絕，只有個別適應能力特別強的物種或者個體得以生存，在“災變”過后重新繁衍后代。顯然“災變”后幸存的物種或個體的生存能力更強［8～10］。

當經過若干代之后，算法中群體已經獲得某個局部最優解，而此時的群體隱含著大量與該局部最優相關的信息，趨向于早熟收斂，依靠交叉和變異等遺傳操作跳出來的可能性較小，這時可以引入“災變”，除了原最好解留下來，其他個體重新隨機產生，獲得一些全局性的有效信息，以較大的概率得到遠離原局部最優，使得在較小的群體規模下獲得較大的多樣性，則可以更有機會擺脫原先的局部最優解，因為現在的候選解往往不再局限于以前的某個角落了［11～12］。

災變因子引入思路簡示如下:

1）災變次數初始化；

2）進行某階段的遺傳進化操作和適應度評估；

3）災變次數增加1；

4）如果達到預定值則輸出結果并結束，否則存當前最好解并返回第2）步。

2.5 基于災變因子的量子遺傳算法

當種群中個體之間的差別很小的時候，認為算法將要陷入不成熟收斂了，此時采用災變算子來提高個體之間的多樣性，以保證算法能夠找到全局最優解。

災變的實施也有很多的方法:1）突然增大變異率；2）保留最好解，重新初始化其他的個體；3）對不同的個體實施不同規模的變異。本文采用的是第二種方法。

基于災變因子的量子遺傳算法流程如圖2。

圖2 基于災變因子的量子遺傳算法

加入災變因子后，當最優值保持一定次數后，則認為進化已經進入了不成熟的收斂階段，設定災變因子disater_factor，當最優值持續一定程度后，保留最優值并對種群進行新的初始化，確保算法跳出局部最優

3 實驗對比

本文采用三個標準函數針對量子遺傳算法與標準遺傳算法作對比:

這幾個典型的標準函數都具有全局極值點，并且有多峰值函數，有多個峰值陷阱，這樣一般優化算法容易陷入局部收斂，用它們來比較各種算法的性能是合適的。在這里種群大小設置為40，最大遺傳代數基礎設置為100，分別測試標準遺傳算法SGA 以及基于災變因子量子遺傳算法QGA 的尋優效果，結果如圖4～6所示。

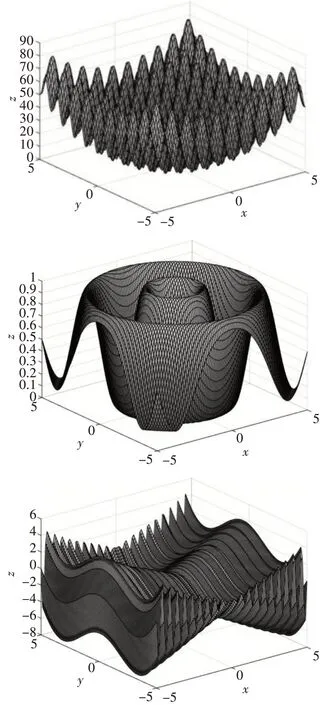
圖3 測試函數空間曲面圖

圖4 F1函數進化代數與最優解變化

圖5 F2函數進化代數與最優解變化

圖6 F3函數進化代數與最優解變化

上圖中，虛線表示標準遺傳算法的最優解與進化代數的關系，實線表示基于災變因子量子遺傳算法的最優解與進化代數的關系。可以得出在多峰值函數尋優過程中，基于災變因子量子遺傳算法收斂速度快，尋優結論相比較之下要比標準遺傳算法更加準確。標準遺傳算法在多峰值情況下的尋優會出現過早收斂，無法調出局部最優的問題，尋優結果不穩定。相比較之下，基于災變因子量子遺傳算法使用量子門對種群進行更新，加入災變因子，更快跳出局部最優，有效阻止了局部最優解的產生，由此可見，基于災變因子的量子遺傳算法與標準遺傳算法相比，由于算法迅速地從某個局部區域中擺脫出來，并在新的解空間中進行繼續的搜索，因而能大大改善了量子遺傳算法的收斂性。

4 結語

基于災變因子量子遺傳算法是在遺傳算法的基礎上，將量子計算在計算方面的優勢引入遺傳算法里，并且引入了災變因子，彌補了傳統遺傳算法的缺陷，它仍屬于遺傳算法的范疇，但比遺傳算法的優化性能高。

本文是通過把基于災變因子的量子遺傳算法和遺傳算法分別應用于三個測試函數進行仿真測試，對測試結果進行圖表分析，然后得出結論。所選的三個測試函數都是具有峰值的函數。從實驗的圖表中可以得出:

1）基于災變因子的量子遺傳算法在對同一峰值函數進行測試求解，所求得的最優解的精確度會隨著其迭代次數的增大而提高。

2）基于災變因子的量子遺傳算法對峰值函數進行測試求解時，在相同的迭代次數下，用量子遺傳算法所求得的峰值函數的最大值的精確度要高于用遺傳算法所求得。

這表明了量子遺傳算法算法在連續空間優化的可行性和有效性，同時也表明了量子遺傳算法算法具有良好的應用前景。