混合式慣導系統姿態四元數連續自標定模型

王琪，汪立新，周小剛，沈強

（火箭軍工程大學 導彈工程學院，西安710025）

混合式慣導系統是一種新型慣導系統，其吸收了平臺式和捷聯式慣導系統的各自優點，并且將隔離載體角運動的物理平臺、捷聯姿態算法與旋轉調制抑制誤差效應這三者集于一體。該系統主要著眼于高速和高動態運載器對高精度慣導提出的新需求，不僅能大幅度提高導航定位精度，實現快速精確自對準，還可實現裝機條件下的自標定以及明顯降低購置和維護成本[1]。

慣性系統誤差標定補償是提高系統精度的有效手段，針對混合式慣導系統三軸全姿態物理平臺和系統裝機自標定的特點，選擇運用連續自標定方法進行混合式慣導系統的誤差自標定。連續自標定是Jackson[2]于1973年提出的一種動態標定方法。其基本原理如下：慣性平臺在外力矩的作用下以角速度ωc（稱為加矩角速度）轉動，在地球自轉角速度、加矩角速度以及重力加速度的激勵下，加速度計輸出中包含有陀螺儀誤差、加速度計誤差、安裝誤差和平臺對準誤差等全部誤差信息。以加速度計輸出為觀測量，以平臺對準誤差方程為動力學模型，采用最優濾波算法估計平臺誤差系數和對準誤差，并用估計結果對平臺模型進行補償與調整[3]。相比于傳統的多位置自標定，連續自標定中慣性平臺轉動的每一個采樣點都相當于多位置自標定中的一個位置，因此連續自標定方法能夠以比多位置自標定更高的精度同時標定出慣性平臺的全部誤差系數。

傳統的連續自標定針對平臺式慣導系統，主要有基于失準角和基于框架角的2種自標定模型。文獻[4]系統地介紹了平臺連續自標定的失準角模型、可觀測性分析、參數辨識等內容。文獻[5-6]針對大失準角情況下傳統的失準角誤差模型會產生較大誤差的問題，建立了框架角誤差模型。文獻[7-8]分析了平臺連續自標定中各誤差系數的可觀測性，并針對安裝誤差可觀測性低這一問題，分別建立了以加速度計輸入軸和陀螺儀輸入軸為基準的平臺坐標系，減少了安裝誤差項，使所有的安裝誤差變得可觀，提高了標定精度。

考慮到混合式慣導系統采用捷聯姿態算法，而捷聯姿態算法中使用姿態四元數來描述物體轉動，四元數表示能夠避免傳統的歐拉角表示中大量的三角運算帶來的舍入誤差，從而提高計算速度和標定精度[9]。以四元數為基礎的四元數卡爾曼濾波（Quaternion Kalman Filter，QKF）在慣性導航系統的姿態估計[10]和自對準[11]問題都已有一定應用。因此本文在混合式慣導系統框架角約束方程的基礎上，利用姿態四元數代替歐拉角描述混合式慣導系統中三軸物理平臺的轉動，建立一種混合式慣導系統姿態四元數連續自標定模型，并且針對這一模型的特點，提出了一種基于奇異值分解的四元數無跡卡爾曼濾波（Unscented Kalman Filter based on Singular Value Decomposition Quaternion，SVD-QUKF）來標定混合式慣導系統誤差系數。通過仿真和試驗比較了基于姿態四元數模型的SVD-QUKF算法和基于框架角模型的UKF算法的標定結果，證明本文提出的自標定模型和標定算法在計算速度和標定精度上較傳統方法都有一定優勢。

1 慣性平臺姿態四元數與框架角之間的轉換關系

首先給出混合式慣導系統中的坐標系定義，混合式慣導系統采用隔離載體角運動的三軸物理平臺，物理平臺通過3個框架軸固聯在基座上，其中慣性平臺固聯在臺體軸上，臺體軸固聯在內環軸，內環軸固聯在外環軸，外環軸固聯在基座上，由此構成具有三自由度的穩定平臺。三軸物理平臺由3個陀螺儀與3個加速度計組成，如圖1所示。定義如下坐標系：

1）框架坐標系（K）：XK、YK、ZK三軸分別指向混合式慣導系統的外框架軸、內框架軸、臺體軸，三者構成右手正交坐標系。

2）平臺坐標系（p）：以加速度計敏感軸為基準定義，取三軸物理平臺幾何中心為原點，Xp軸與X加速度計敏感軸平行，Yp軸平行于X和Y加速度計敏感軸所確定的平面，并與Xp軸垂直，Zp軸與Xp軸以及Yp軸構成右手正交坐標系。

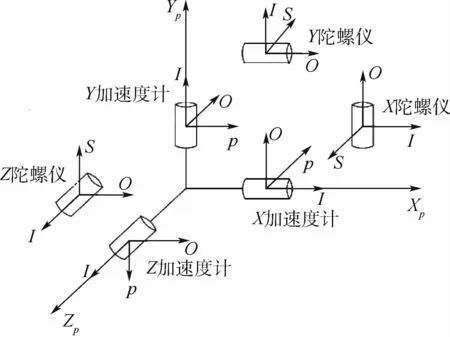
圖1 三軸物理平臺組成Fig.1 Three-axis physical platform geometry

根據慣性平臺臺體和3個框架軸之間的固聯關系可知，無論3個框架軸如何轉動，都可以通過繞ZK—YK—XK軸的順序使平臺臺體轉回原位置，對于p系來說，就是繞Yp—Xp—Zp軸的順序轉回原位置。若假設慣性平臺繞XK、YK和ZK軸轉動角度分別為 θx、θy和 θz，則對于p系來說，就是依次繞Zp、Xp和Yp軸分別轉動 θx、θy和 θz。根據四元數定義，描述慣性平臺轉動的姿態四元數為

同時，姿態四元數到框架角的轉換關系為

2 混合式慣導系統連續自標定模型

2.1 混合式慣導系統框架角約束方程

混合式慣導系統在地面標定時處于穩定和穩定加旋轉2種工作模式[1]，此時混合式慣導系統的工作原理與平臺式慣導系統相同，因此可以采用平臺式慣導系統的框架角約束方程。利用框架角約束方程建立自標定模型能夠避免失準角模型中的小角度假設，從而能夠適用于大失準角的情況。假設慣性平臺繞XK、YK和ZK框架軸轉動的框架角分別為 θx、θy和 θz，則其框架角約束方程為[6]

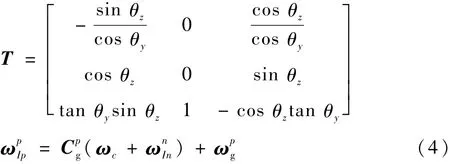
In=[0 ωIEcos L ωIEsin L]T，ωIE為地球自轉角速度值，L為當地緯度；ωpg為平臺漂移，由陀螺儀誤差引起的，混合式慣導系統所用的光纖陀螺儀具有很好的線性度，二次項誤差基本可以忽略不計[12]，只需要考慮其零偏誤差和隨機誤差，所以有

式中：kg0i（i=x，y，z）為陀螺儀零次項誤差系數；εgi為陀螺儀量測噪聲。

2.2 加速度計輸出方程

加速度計的輸出與加速度計三軸敏感的比力有關，加速度計三軸上的比力為

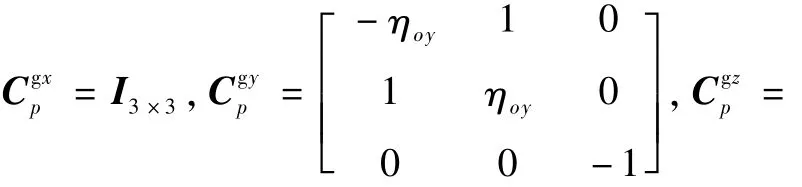
則加速度計輸出方程為[13]

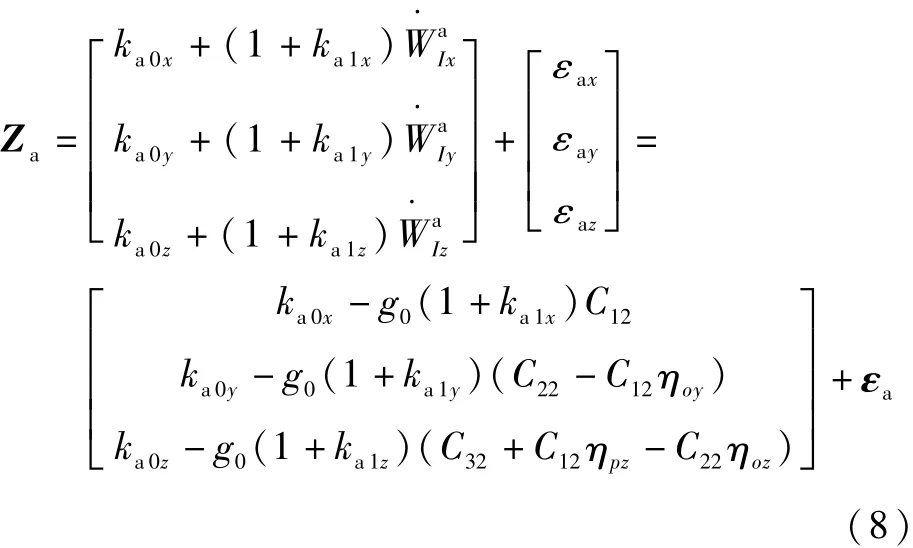
式中：kaji（j=0，1；i=x，y，z）為加速度計誤差系數；εa為加速度計量測噪聲；Cmn（m，n=1，2，3）為矩陣Cpn的元素。

以框架角約束方程為系統方程，以加速度計輸出和框架角傳感器輸出為系統量測，結合式（3）～式（5）和式（8），則可以得到基于框架角的連續自標定模型（以下簡稱為框架角模型）為

2.3 四元數連續自標定模型

對式（1）進行求導，整理可得四元數微分與框架角微分之間的關系為

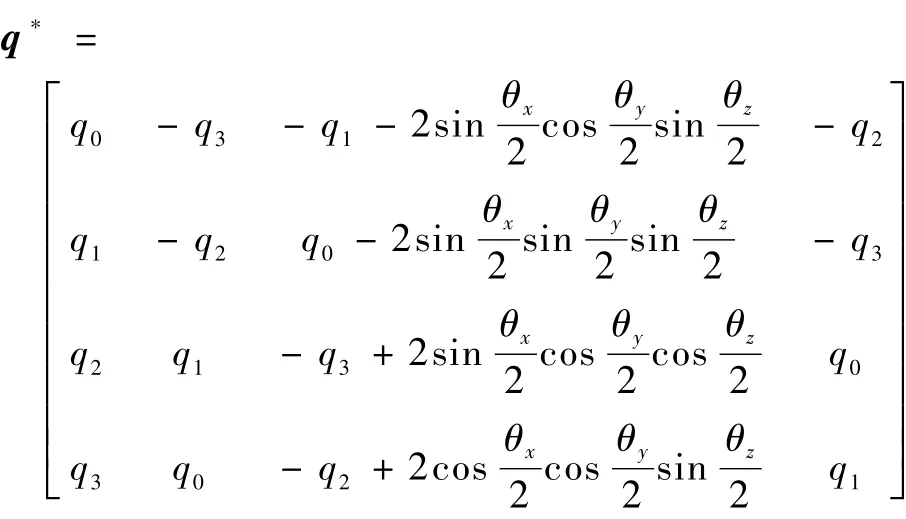
式中：Tq為矩陣T的四元數表示。

考慮框架角傳感器的量測噪聲，將 θi+vi（i=x，y，z）代入式（1）可得帶有噪聲干擾的四元數為

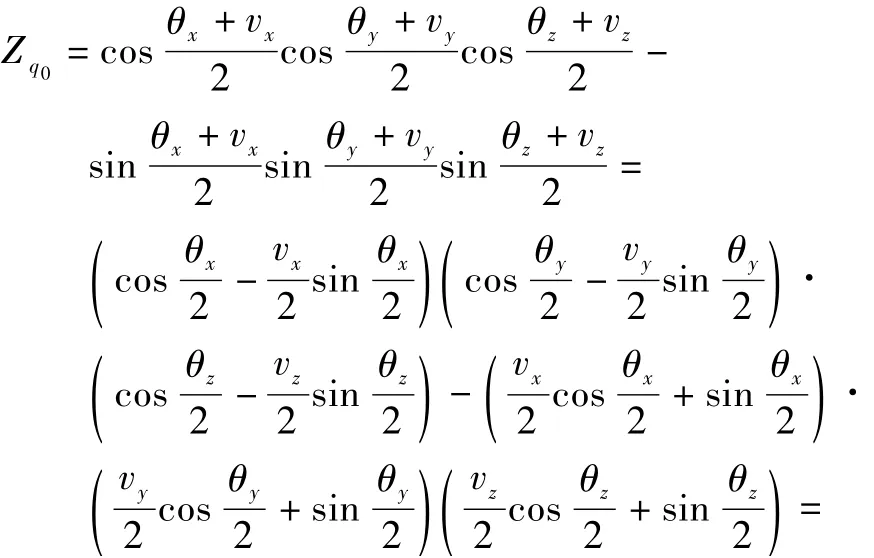
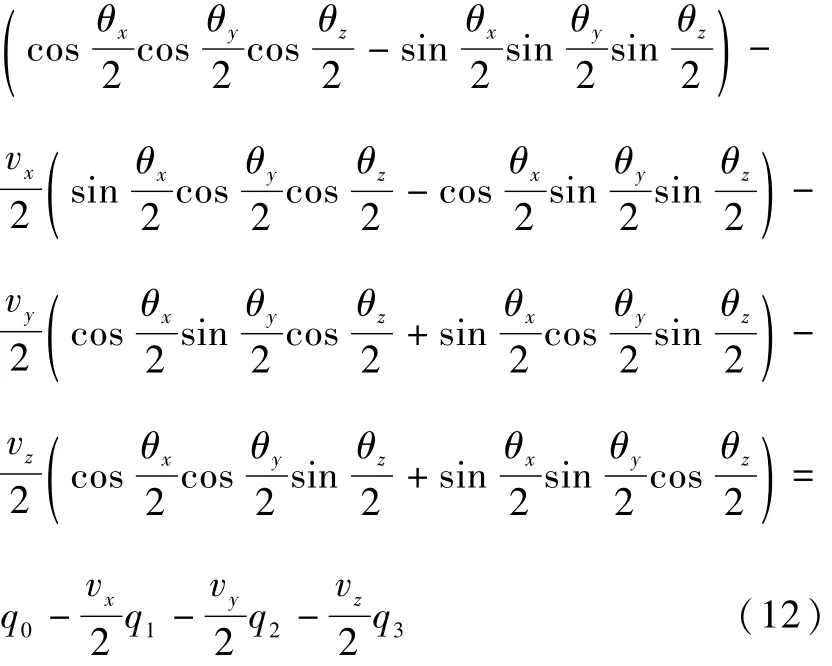
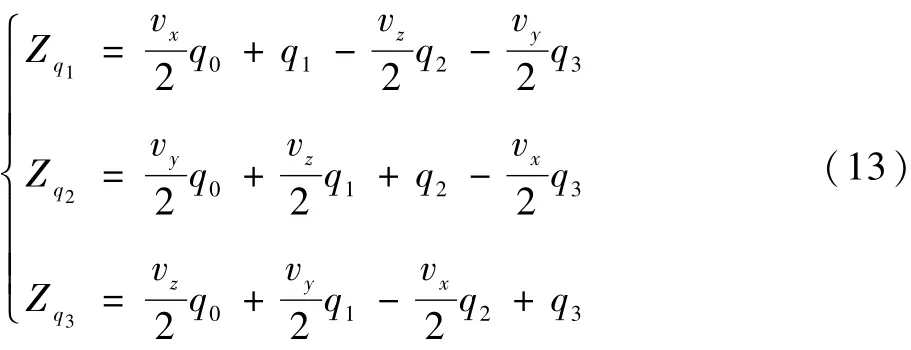
同理可得

因此，包含噪聲的姿態四元數量測方程為

式中：

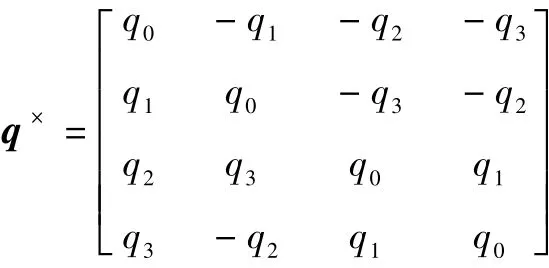
同時用Cpnq代替式（8）中的Cpn，則式（9）中的觀測方程可以寫為

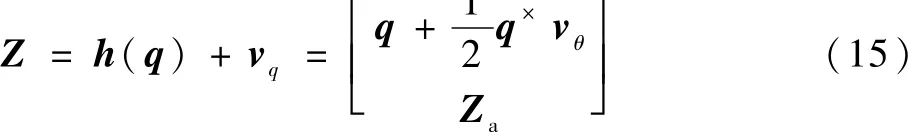
結合式（11）和式（15），可得混合式慣導系統的四元數連續自標定模型（以下簡稱為四元數模型）為

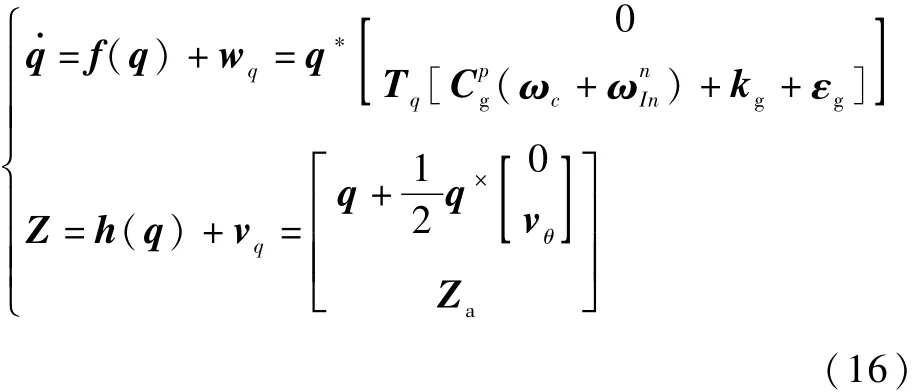
混合式慣導系統采用捷聯姿態算法，而捷聯姿態算法中使用姿態四元數來描述物體轉動，四元數模型正好滿足這一要求。同時，四元數表示能夠避免傳統的歐拉角表示中大量的三角運算帶來的舍入誤差，提高計算速度和標定精度，并且四元數表示不存在奇異點，因此能夠避免慣性平臺連續轉動過程中可能出現的“框架自鎖”現象。

3 基于奇異值分解的四元數無跡卡爾曼濾波

可以看出，式（16）的四元數模型是一個強非線性的系統方程，因此選擇UKF對其進行狀態估計和參數辨識。但是有2個問題需要解決：①在UKF濾波過程中，由于量測噪聲、截斷誤差和狀態模型擾動等因素的影響，狀態協方差矩陣P容易變得非正定，然而在UKF中利用Cholesky分解獲取σ樣本點時，要求P必須正定；②在將歐拉角表示轉換為四元數表示之后，原來3維的系統噪聲和量測噪聲都變成了4維噪聲，系統噪聲方差陣Q和量測噪聲方差陣R的形式也隨之發生變化，需要重新進行推導。

3.1 奇異值分解

針對第一個問題，本文選擇奇異值分解代替Cholesky分解來獲取σ樣本點。因為奇異值分解不要求被分解矩陣為正定，同時，如果被分解矩陣是正定的，那么奇異值分解和Cholesky分解的結果是相同的[14]。奇異值分解的結果為

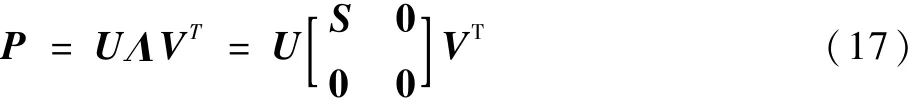
式中：P∈Rm×n，m≥n；Λ∈Rm×n；U∈Rm×m；V∈Rn×n；S=diag（s1，s2，…，sr），s1≥s2≥…≥sr≥0為矩陣P的r個奇異值，r=rank（P）。

3.2 系統噪聲方差陣和量測噪聲方差陣的推導

根據系統噪聲方差陣Q和量測噪聲方差陣R的定義，有Q=E[wwT]和R=E[vvT]。根據2.3節中的推導可知，在將歐拉角表示轉換為四元數表示之后，系統噪聲和量測噪聲變為wq=，則四元數表示的系統噪聲方差陣Qq和量測噪聲方差陣Rq的表達式有如下推導：

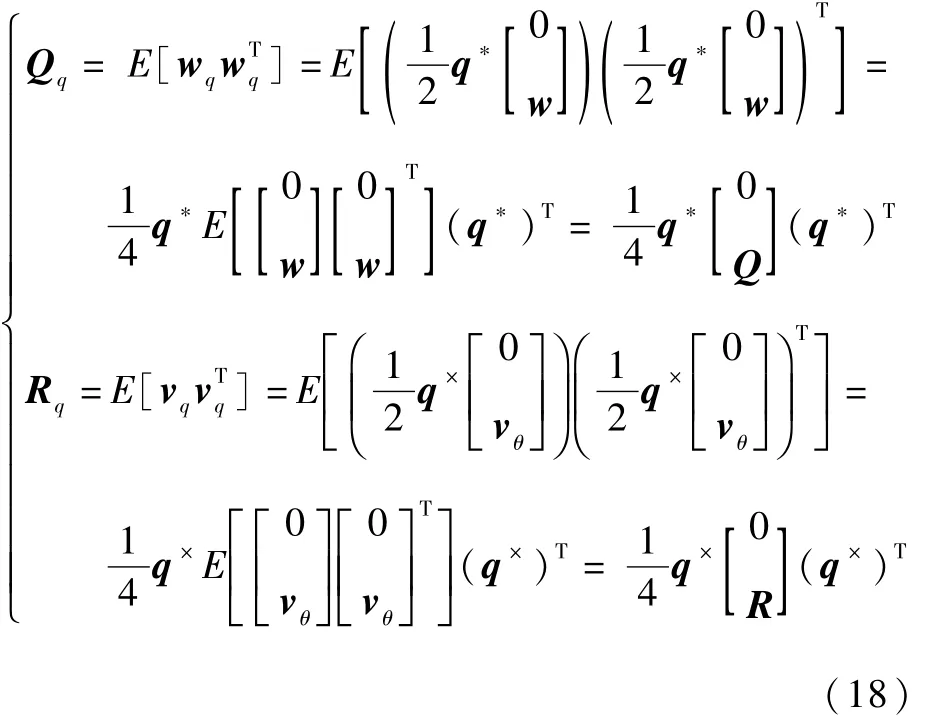
式中：Qq，Rq∈R4×4。

3.3 SVD-QUKF算法步驟

在將歐拉角表示轉換為四元數表示之后，系統噪聲wq和量測噪聲vq由加性噪聲變為了非加性噪聲，此時需要將其擴展為系統狀態量[15]。此外，待標定的慣導系統誤差系數也擴展為系統狀態量，則擴展后的系統狀態量為

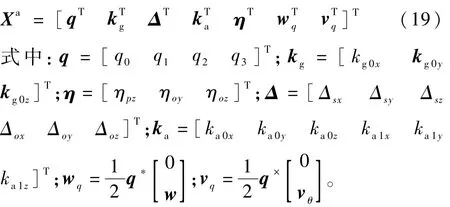
狀態協方差矩陣P為

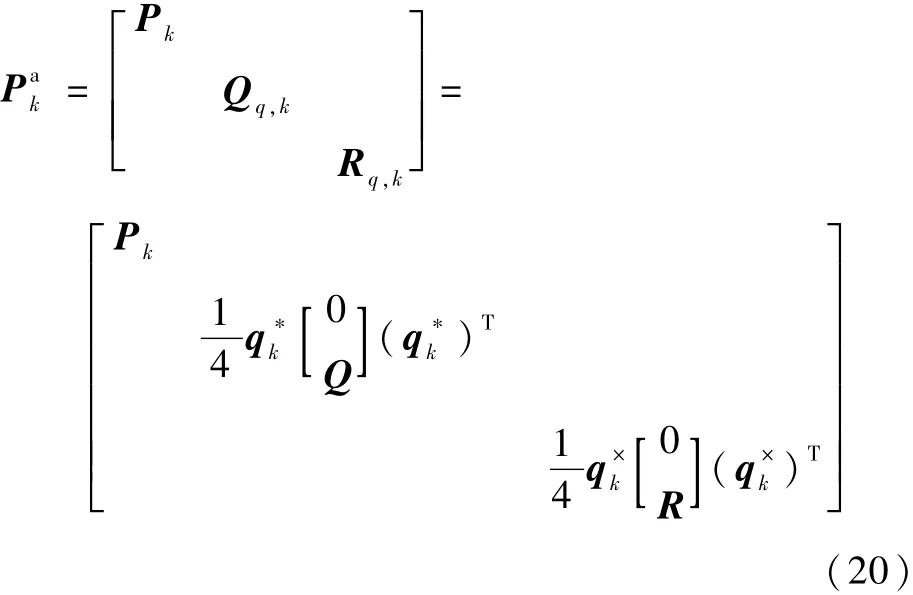
對式（16）進行離散化，則可得到SVD-QUKF的濾波方程為

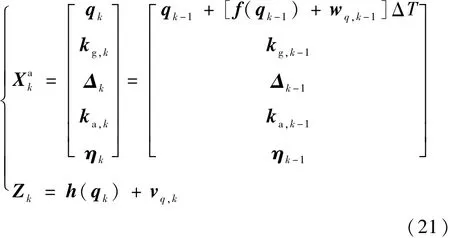
式中：ΔT=0.2 s為離散時間間隔。

則SVD-QUKF的算法步驟如下：

1）濾波初值

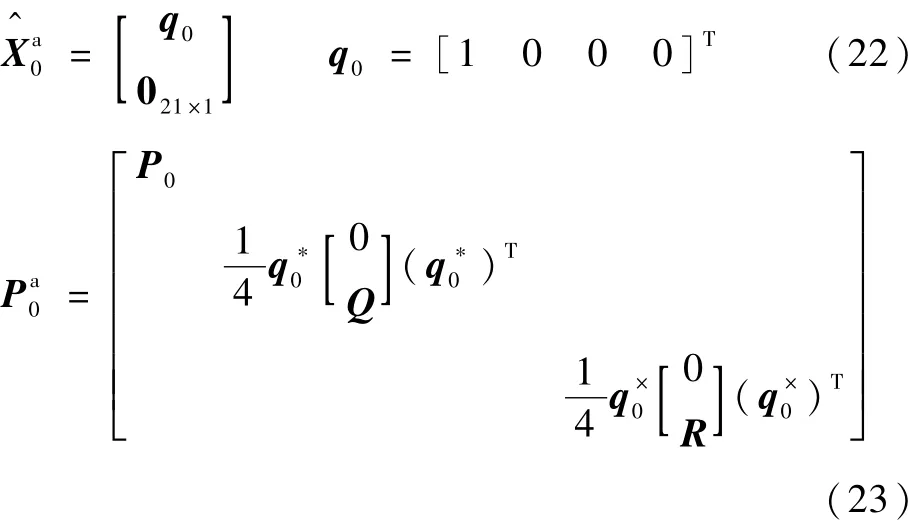
2）計算σ樣本點

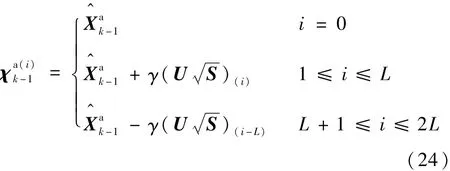
式中：U和S為式（17）中狀態協方差矩陣P的SVD分解結果

3）時間更新

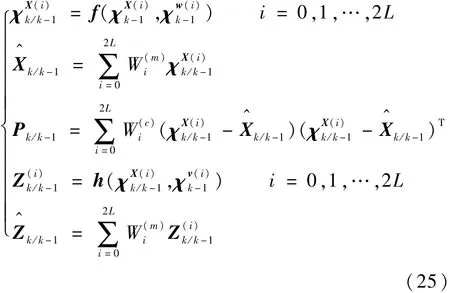
4）量測更新

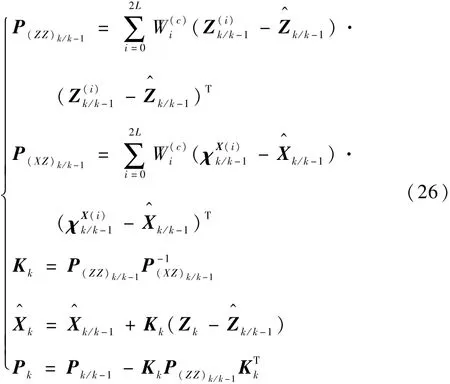
5）歸一化

在每一次迭代之后，都需要對姿態四元數進行歸一化以保證其為標準四元數[16]，即

4 仿真和試驗

4.1 仿真分析

為驗證本文提出的四元數模型的適用性，運用SVD-QUKF算法對式（16）的四元數模型進行了參數辨識，運用UKF算法對式（9）的框架角模型進行了參數辨識，對二者結果進行對比。混合式慣導系統三軸物理平臺的轉動路徑如下[17]：

1）起始角度為 θx=0°，θz=0°，以 角 速 度1（°）/s繞ZK軸轉動 π。

2）起始角度為 θx=0°，θz=π，以角速度1（°）/s繞XK軸轉動 π/2。

3）起始角度為 θx=π/2，θz=π，以角速度1（°）/s繞ZK軸轉動 π。

4）起始角度為 θx=π/2，θz=0°，以角速度1（°）/s繞XK軸轉動 π/2。

定義系統狀態量的估計誤差和相對估計誤差以表示標定精度：

式中：Δx為估計誤差；e為相對估計誤差；x^和x分別為系統狀態量的估計值和真值。

首先，為了比較2種系統模型對框架角的估計精度，將框架角模型估計得到的框架角轉換為四元數與四元數模型估計得到的四元數進行了對比，估計誤差如圖2所示。

從圖2可以看出，四元數模型對于框架角的估計誤差小于框架角模型，所以對于框架角的估計精度，本文提出的四元數模型要優于傳統框架角模型。

其次，為比較2種模型對于混合式慣導系統誤差系數的標定精度，表1給出了所有誤差系數在2種系統模型下的相對估計誤差和算法計算時間，圖3給出了部分誤差系數的相對估計誤差曲線。

從表1可以看出，使用SVD-QUKF的四元數模型的計算時間遠少于使用UKF算法的框架角模型，這是因為SVD-QUKF算法中采用的四元數表示避免了歐拉角表示中大量的三角運算，從而減少了計算時間。在實際的慣導系統自標定中，是采用實時濾波的方法進行誤差系數辨識，根據仿真時間可得，原始算法進行一個卡爾曼濾波周期需要13 ms，這已經比較接近于一般慣導系統20 ms的計算周期，不利于進行實時濾波，而本文的算法進行一個卡爾曼濾波周期所需時間為7 ms，能夠保證實時性要求。同時可以看出，在相同的轉動路徑和仿真條件下，四元數模型對于混合式慣導系統誤差系數的估計精度也要優于傳統的框架角模型，特別是對于陀螺儀和加速度計的安裝誤差系數的標定精度提高較大。仿真結果表明，相比于傳統的框架角模型，本文提出的四元數模型能夠有效提高混合式慣導系統的誤差系數標定精度。

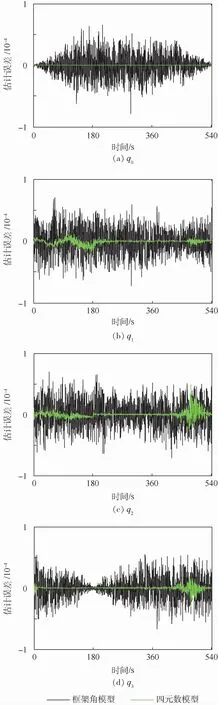
圖2 四元數模型和框架角模型的框架角估計誤差曲線Fig.2 Estimate error curves of gimbal angle in quaternion model and gimbal angle model

4.2 試驗驗證

在某型平臺式慣導系統上進行了試驗驗證。

表1 誤差系數相對估計誤差和算法計算時間Table 1 Computing time and relative estimate er rors of error coefficients

由于硬件限制，試驗中只各繞ZK軸和XK軸進行了一次轉動：

1）起始角度為 θx=0°，θz=0°，以 角 速 度1（°）/s繞ZK軸轉動 π。

2）起始角度為 θx=0°，θz=π，以角速度1（°）/s繞XK軸轉動 π。

采集加速度計和框架角傳感器的輸出，利用傳統的框架角模型和本文提出的四元數模型進行了誤差系數標定，對于框架角的估計誤差如圖4所示，其均方根誤差（RMSE）如表2所示。從圖4和表2可以看出，四元數模型對于框架角的估計精度要高于框架角模型，從而驗證了其適用性。同時可以注意到，在圖4中，在繞ZK軸轉動完畢和剛開始繞XK軸轉動時，估計誤差會發生較大的波動，這是因為當加速度計接近水平位置時，加速度計輸出中噪聲比很大，從而會造成濾波結果偏離真值，甚至有可能導致濾波結果發散，這種情況是需要避免的。具體做法是：在設置自標定程序時，根據框架角傳感器的輸出判斷加速度計是否接近水平位置，當加速度計接近水平位置時，斷開加速度計的輸出采集回路，同時停止濾波，待加速度計離開水平位置一定角度后，再重新采集加速度計輸出，繼續進行濾波。

圖3 k a0i（i=x，y，z）和 ηji（j=p，o；i=y，z）的相對估計誤差曲線Fig.3 Relative estimate error curves of k a0i（i=x，y，z）andηji（j=p，o；i=y，z）

圖4 試驗中四元數模型和框架角模型的框架角估計誤差曲線Fig.4 Gimbal angle estimate errors of quaternion model and gimbal angle model in experiment

表2 四元數模型和框架角模型的框架角均方根誤差Table 2 RMSE of gimbal angle of quaternion model and gimbal angle model

5 結 論

1）針對混合式慣導系統全姿態物理平臺、捷聯姿態算法和系統裝機自標定的特點，本文在混合式慣導系統框架角約束方程的基礎上，利用姿態四元數代替歐拉角描述混合式慣導系統中三軸物理平臺的轉動，建立一種姿態四元數連續自標定模型。

2）針對四元數連續自標定模型的特點，對傳統的UKF算法進行改進，利用SVD 代替傳統UKF算法中的Cholesky分解來獲取σ樣本點，避免了狀態協方差矩陣P不正定時Cholesky分解結果奇異的現象；同時推導了四元數表示下的系統噪聲方差陣Qq和量測噪聲方差陣Rq，將3維噪聲轉換為了4維噪聲，提出了一種SVD-QUKF算法用于標定混合式慣導系統誤差系數。

3）仿真和試驗結果表明，相比于基于傳統UKF算法的框架角連續自標定模型，本文提出的四元數連續自標定模型和SVD-QUKF算法能夠以低于1%的相對誤差標定出混合式慣導系統所有的誤差系數，在標定精度和計算速度上都有一定優勢，具有實用價值。