基于遺傳算法與邊界元理論的聲屏障優化

鄧友生， 段邦政， 葉萬軍， 景宏君， 吳 鵬

(1.西安科技大學建筑與土木工程學院，陜西西安 710054；2.湖北工業大學土木建筑與環境學院，湖北武漢 430068)

隨著高速鐵路、城市軌道交通及高速公路的快速發展，交通噪聲對公眾環境及健康的危害日益嚴重[1]。作為改變聲波傳播途徑的降噪手段之一，聲屏障因降噪效果好、建造維護方便等優點廣泛應用于國內外高速鐵路及高等級公路。泡沫混凝土作為一種多孔吸聲材料[2]，具有良好的可塑性，將其制成聲屏障是對噪聲污染嚴重人居區域的一種經濟有效的降噪措施。

國內外學者對遺傳算法和邊界元理論在聲學領域的應用進行了大量研究。文獻[3]運用遺傳算法對內燃機油底殼的噪聲進行優化控制，優化后的噪聲輻射聲功率級最大可降3.3 dB，聲功率級最大可降低8.21 dB。文獻[4]結合二維邊界元理論研究高速鐵路不同幾何形狀聲屏障的降噪效果和降噪機理，Y形聲屏障的插入損失比一般形式聲屏障高3.4 dB。文獻[5]結合邊界元理論研究聲屏障截面形式對插入損失的影響，聲屏障降噪效果的降序排列為Y形、傾斜型、T形、外折型、直立型、內折型。文獻[6-8]基于遺傳算法和耦合邊界元法，考慮吸聲材料的流阻，并結合成本函數對T形聲屏障進行優化。文獻[9]運用遺傳算法優化聲屏障的頂端結構，研究表明：T形聲屏障降噪效果比直壁型好，其插入損失比直壁型高5 dB。文獻[10]基于遺傳算法理論，運用雙重邊界元法研究雙層薄壁聲屏障(隔聲屏障外覆蓋吸聲屏障)的聲學特性。

本文基于遺傳算法、聲屏障邊界元理論及成本效益分析法，針對由高速鐵路及高速公路引起的交通噪聲，優化聲屏障的高度、組合形式及頂端結構類型;結合聲屏障聲學測量規范對優化的聲屏障結構進行模型試驗，同時將測量數據與理論分析結果進行對比，驗證理論分析的正確性。

1 交通噪聲

交通噪聲主要是由機動車輛在交通干線上運行時所產生的噪聲疊加而成，其噪聲來源[11]主要包括輪胎與地面之間空氣在壓縮和釋放時所產生的空氣泵噪聲、動力系統噪聲和路面不平整所引起的振動噪聲。交通噪聲具有時域和頻譜兩大特性，其時域變化規律隨著交通流的改變而變化；頻譜特性是交通噪聲的固有特性，頻率是研究聲屏障聲學特性最重要的參數之一。 我國交通噪聲頻率范圍為250～2 000 Hz[12]，交通噪聲頻譜如圖1所示。

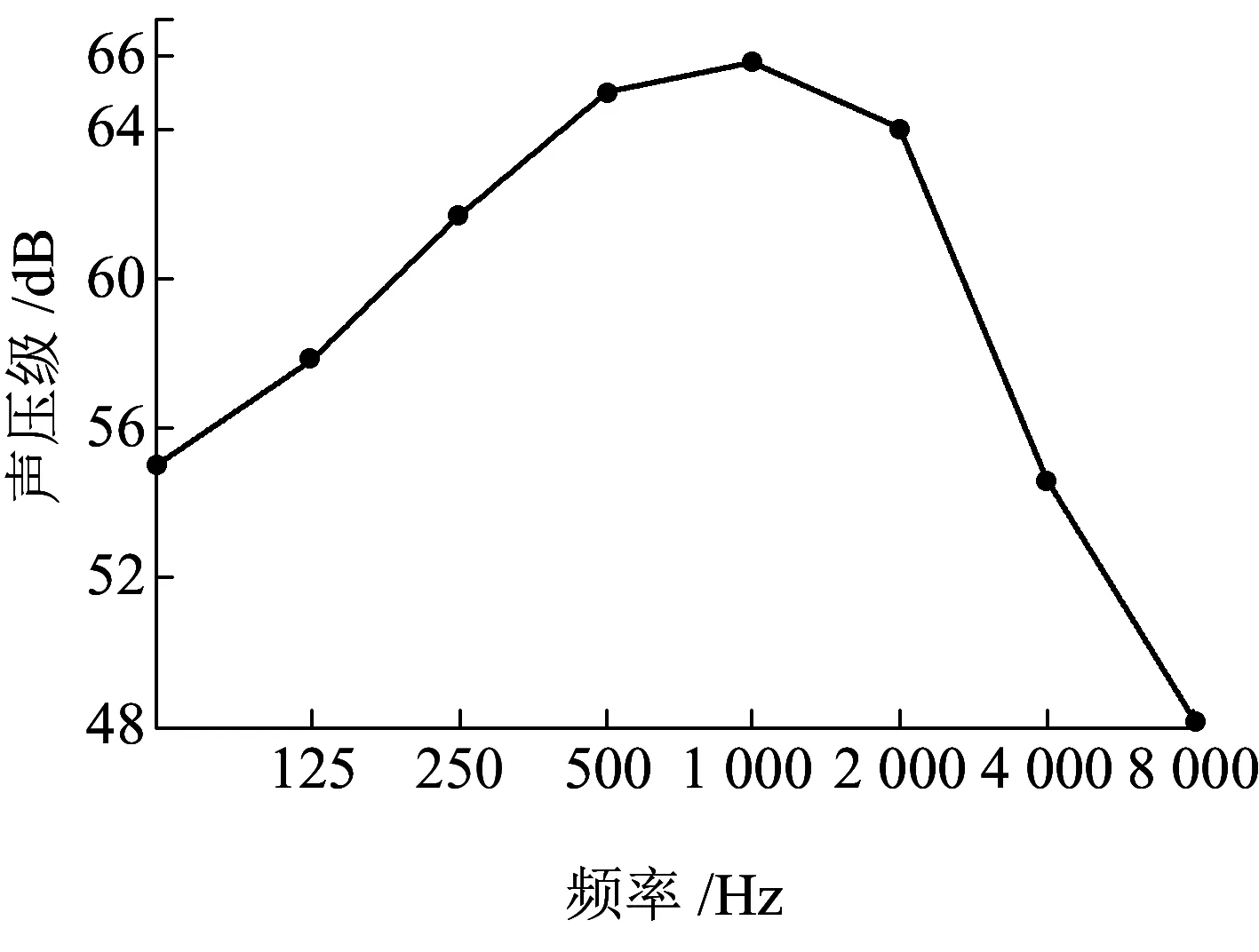
圖1 交通噪聲頻譜

交通噪聲污染已經成為世界環境公害，其危害體現在影響情緒、損害交感神經[13]、降低土地使用價值等方面。交通噪聲的防治是保障人們正常學習、生活和工作的聲環境質量，構建和諧社會，促進經濟可持續發展的前提。目前國內外交通噪聲的防治[12]主要有綠化降噪處理、聲屏障降噪處理、研究低噪聲交通工具等方法。

2 聲屏障優化計算

2.1 邊界元理論及計算模型

邊界元法是一種研究聲屏障插入損失的數值工具[4-5,14]，其常應用于二維或三維空間來模擬聲屏障復雜的截面形式及頂端結構。邊界元法以邊界積分方程為控制方程，通過對邊界進行離散化，將積分問題轉化為代數方程組來求解。與有限元法相比，邊界元法降低了維度，從而降低了自由度，使問題簡單化。

聲屏障的邊界元模型常選用二維邊界元模型。為簡化聲屏障的邊界元模型，本文對其做如下假定[15]：

(1)假定聲屏障放置的平面無限長且均勻；

(2)假定聲屏障周圍的介質是均勻的。

基于以上兩個假定，道路、噪聲源(可視為沿鐵路或公路方向的無限長線聲源)及聲屏障三者相互平行，即三者在同一個平面內，因此噪聲三維聲場分布可轉化為二維聲場分布，如圖2所示。

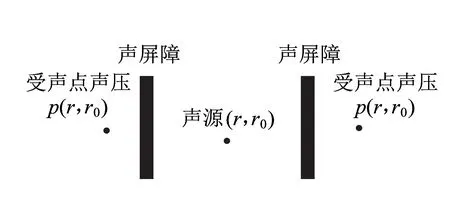
圖2 聲屏障的二維邊界元模型

聲屏障在聲場區域內可視為散射體，假設線聲源位于r0處，p(r,r0)表示受聲點聲壓，s為聲屏蔽邊界面，rm為邊界面s上任意一點，β(rm)為點rm的法向導納。受聲點的聲場分布可由聲源的入射聲場和聲屏障的散射聲場疊加而成。結合散射聲壓在無窮遠處滿足Sommerfeld 輻射條件[16]與聲屏障局部反應的邊界條件，基于Green函數法及Green第二定理對Helmholtz方程進行求解，可得[8]

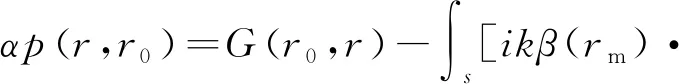
(1)

將聲屏障邊界離散化，即將聲屏障邊界面s劃分成i個線單元si(i=1,2,…，t)，p(rj,r0)代表第j個單元的聲壓，那么可得到關于聲屏障邊界上各單元聲壓值p1,p2,…,pt的t維線性方程組

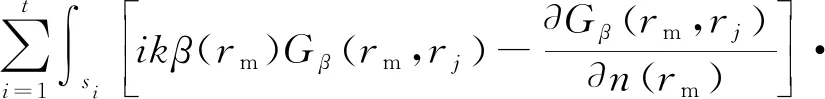
(2)

式中：Gβ表示無聲屏障時的邊界某單元聲壓。運用矩陣解耦運算求解式(2)中邊界上各點的聲壓值p1,p2,…,pt，結合其與無聲屏障時的邊界聲壓Gβ(r0,r)對聲場中任意點的聲壓值進行求解。

(3)

頻帶聲功率反映聲源在單位時間內在一定頻率范圍內向外輻射聲能的大小，噪聲的頻帶聲功率反映了聲屏障插入聲場區域后對噪聲輻射效率的影響。噪聲的聲功率插入損失LIW為聲屏障插入前后聲源的聲功率之差，故聲場中任意點的聲功率插入損失為

(4)

式中：ds為受聲場點的面積微元；G(s)為無聲屏障時聲壓在受聲場點的分布；p(s)為有聲屏障時聲壓在受聲場點的分布；ρc為媒質的特性抗阻。

聲屏障的插入損失LIL為聲屏障插入前后聲壓級之差，故聲場中任意點的聲屏障插入損失為

(5)

2.2 遺傳算法

遺傳算法是一種基于達爾文生物進化論與孟德爾自然遺傳機制的搜索算法[17]，由John Holland教授于1975年提出。生物遺傳概念與遺傳算法是一一對應的關系，見表1。

表1 生物遺傳概念與遺傳算法的對應關系

與其他算法相比，遺傳算法主要具備算法不受約束條件限制、降低極值代替最值的可能性、算子規則隨機、算法隱含并行性等特點。遺傳算法優化模型的基本操作如下。

步驟1建立符合實際情況的優化模型。

步驟2編碼。遺傳算法的編碼方法主要有二進制、格雷碼、多參數級聯等方法，最基本的編碼方法是二進制編碼方法，其參數的表示形式是由二進制編碼符號0和1組成的符號串。

步驟3初始種群。

步驟4評價種群內個體的適應度。若個體適應度收斂則輸出最優解，若不收斂，進行步驟5。

步驟5選擇高適應值的個體，并將優選的個體進行繁殖處理。

步驟6交配。隨機選取兩個優選的個體作為父代，按交換概率Pc進行交換，基于交換的原理，將優選的個體進行基因重組，從而產生新的個體。單點交換示意如圖3所示，圖中“^”表示單點交換的交換位置。

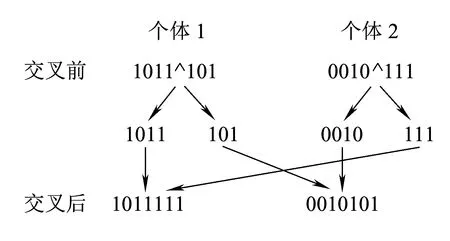
圖3 單點交換示意

步驟7變異。在遺傳信息傳遞的過程中，按變異概率Pm對個體的基因進行變異，以保證種群的多樣性。單點變異法在個體編碼符號串中隨機將某一位置的1變成0或者將0變成1，單點變異示意如圖4所示，其中“_”表示變異位置。

圖4 單點變異示意圖

步驟8對上述產生的種群個體的適應度進行評價，并重復進行步驟4～步驟8。

遺傳算法優化模型時，其參數的選取對計算機的運行結果和運行效率有很大的影響，因此合理選取參數對高效高精度地優化模型具有深遠意義。遺傳算法的參數主要有種群數目N、交換概率Pc，結合大量遺傳算例的經驗，一般種群的種群數目N取30～160；交換概率Pc一般取0.25～0.75。

3 模型的建立與應用

基于遺傳算法及聲屏障的邊界元模型理論，運用MATLAB程序語言對其進行矩陣解耦，并將場點的入射聲壓與散射聲壓進行疊加。結合聲功率插入損失LIW、聲屏障的插入損失LIL及聲屏障的成本，運用聲屏障的成本效益分析方法對聲屏障進行評價。考慮到計算的復雜性，針對交通噪聲的頻譜特性，本文選取聲壓在頻帶內A計權的方法對聲屏障的插入損失進行分析。

公路計算模型選取雙向八車道，選取干密度為600 kg/m3、厚度為5 cm的泡沫混凝土作為聲屏障的吸聲材料，其吸聲性能如圖5所示，泡沫混凝土性能參數見表2。設噪聲源位于道路中心線上，其高度為0.5 m；聲屏障與聲源的水平距離為7.5 m，兩側布置，其高度為h；受聲場點是以噪聲源為中心點，兩側水平距離各為80 m且高度為5 m的平面受聲場點。

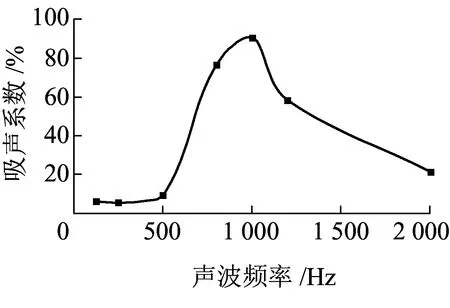
圖5 泡沫混凝土的吸聲性能

參數取值彈性模量/GPa1.5泊松比0.2聲阻抗/(kg·m-2·s-1)1.05×106

3.1 成本效益分析(CBA)

成本效益分析(CBA)方法是結合項目全部成本及收益評估項目價值的方法，CBA在國內外常用于評估和量化具有社會效益的公共事業。聲屏障作為一項公共設施，其社會效益宜選用成本效益方法進行評價。聲屏障的效益評價與聲功率插入損失線性正相關，即

B=b·LIW(h)

(6)

式中：b為聲屏障的社會效益價值系數，一般取1.0～2.0；LIW(h)為聲功率插入損失函數。

基于Schultz曲線(環境干擾度曲線)，文獻[18]選用聲屏障的效益價值比Br作為評價聲屏障的標準，即

Br=B/C

(7)

式中：B為效益；C為成本。

3.2 聲屏障的高度

聲屏障的高度設計是聲屏障環境聲學中最重要的設計部分，其設計的合理性與聲屏障的降噪效果、聲屏障的成本有直接關系，故擬用不同高度的雙側直立聲屏障，運用MATLAB編程計算不同高度下的聲功率插入損失LIW及聲屏障的插入損失LIL，并結合CBA對聲屏障的高度進行評價及優化。

聲屏障高度對聲功率插入損失的影響如圖6所示。由圖6可知，隨著聲屏障高度的增加，聲功率插入損失逐漸增加且增加趨勢趨于平緩。隨著聲屏障高度的增加，聲波的繞射路程及聲屏障的吸聲面積增加，聲源的輻射聲功率降低，使聲功率的插入損失增加。但由于聲波繞射路程的增加速率和聲屏障的吸聲有效面積均隨著聲屏障高度的增加而降低，噪聲聲功率的衰減速率降低，從而導致聲功率插入損失增加趨勢趨于平緩。運用SPSS軟件對圖6的曲線進行擬合，聲功率插入損失LIW與聲屏障高度h呈對數函數關系。由LIW與h的顯著性與相關性分析可知，兩者呈現顯著相關性，其相關性系數為0.935，其函數關系表達式為

LIW(h)=ln[10.23(h-1.65)-1.18]

(8)

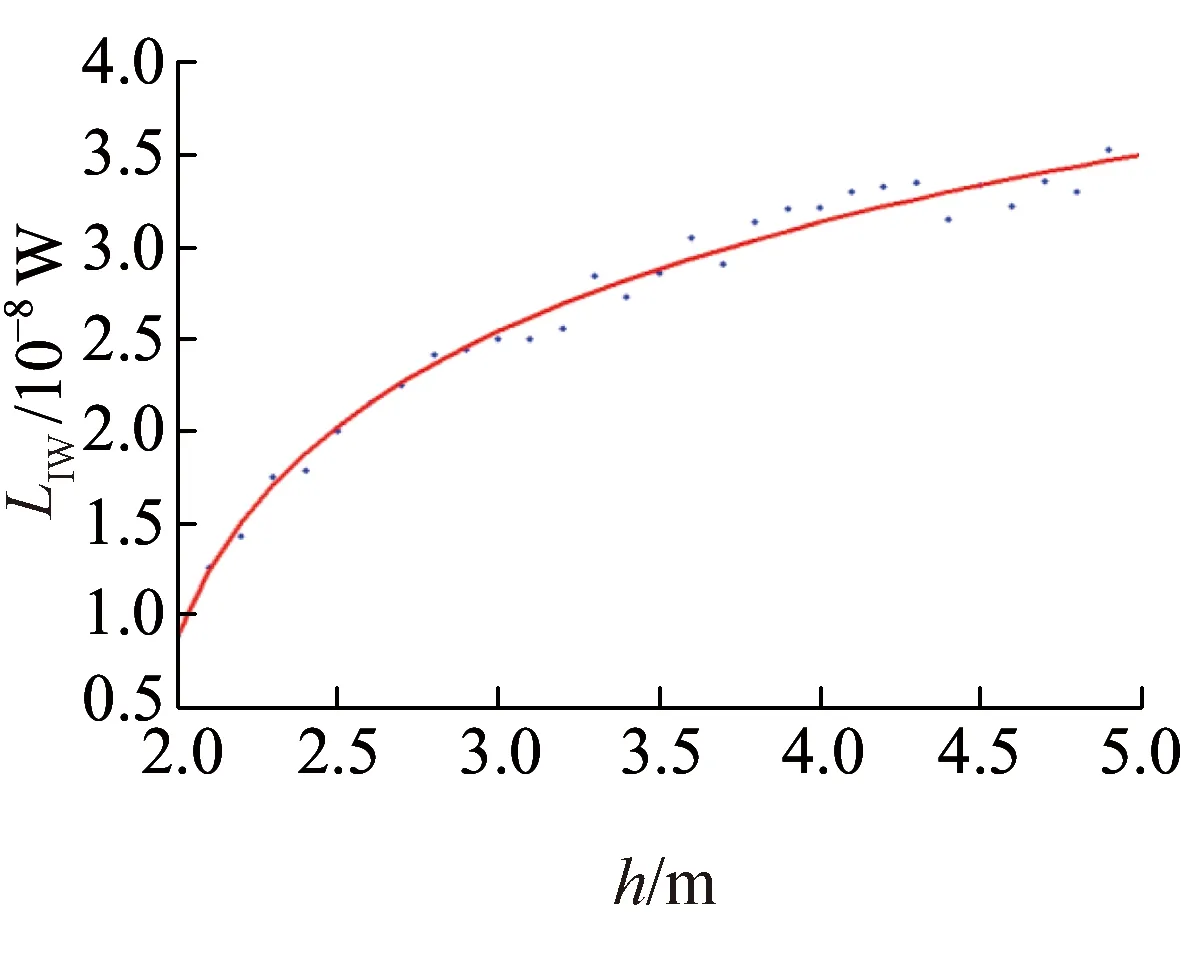
圖6 聲屏障高度對聲功率插入損失的影響

聲屏障成本主要包括：制作成本、運輸成本及安裝成本，總成本C可近似為關于聲屏障高度h的線性函數，設a(a>0)為單位高度聲屏障的成本，即

C=ah

(9)

結合式(6)～式(9)，可以得到聲屏障高度的效益價值比

(10)

聲屏障高度的效益價值比Br關于高度h的變化如圖7所示。由圖7可知，隨著聲屏障高度的增加，聲屏障的效益價值比先增大后減小，在聲屏障高度為2.8 m時，聲屏障的效益價值比達到最大。這是因為隨著聲屏障的高度增加，聲屏障效益的變化規律與聲功率插入損失均呈現增長放緩的趨勢，而聲屏障成本仍處于持續增長的狀態。

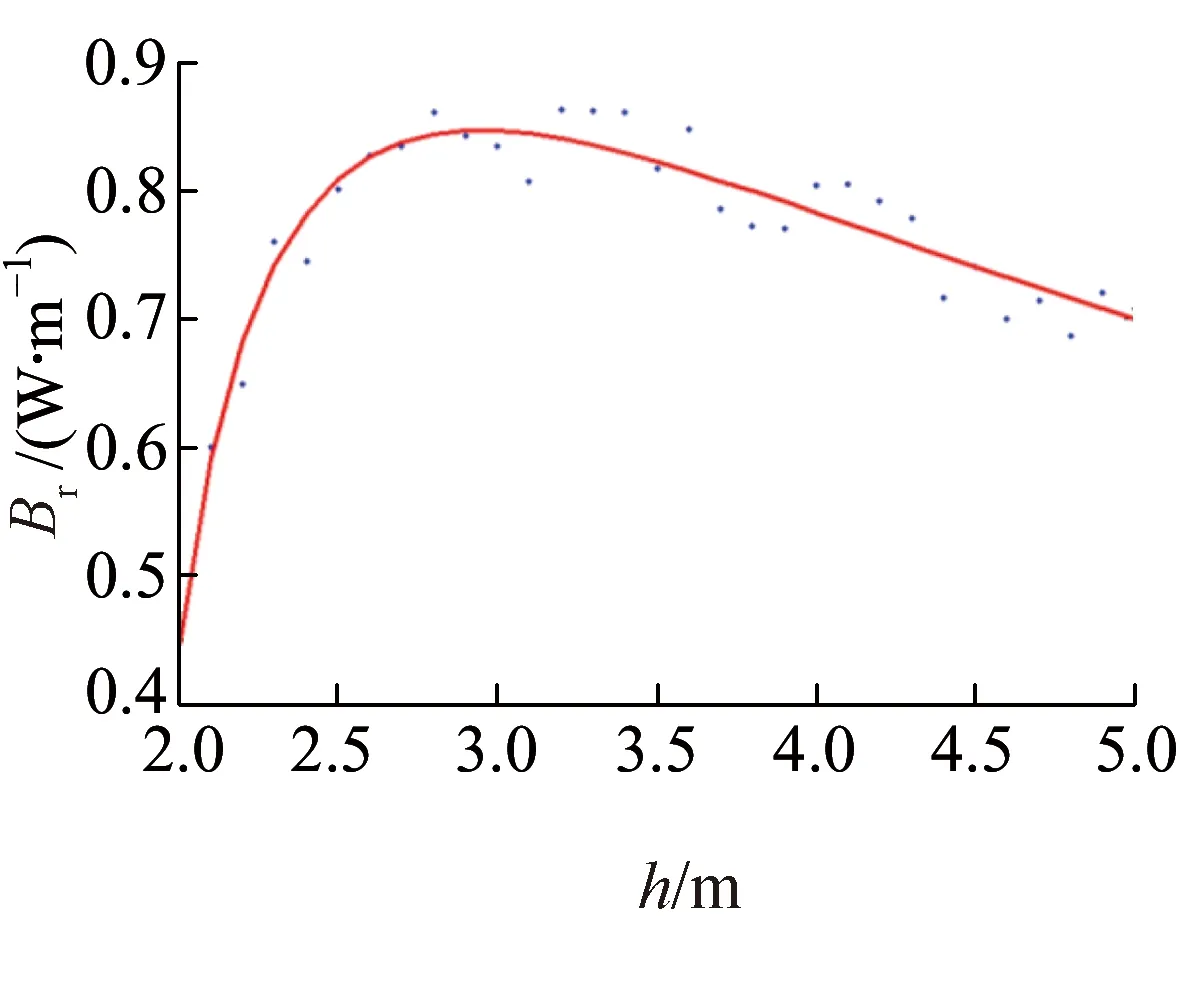
圖7 聲屏障高度的效益價值比函數圖

吸聲型聲屏障插入損失在場點內分布如圖8所示。在聲屏障之間，聲屏障插入損失幾乎為0，這是由于聲波入射到吸聲型聲屏障上，大部分聲能被吸聲材料吸收，反射聲能很小，反射聲波與入射聲波無法形成較強的干涉現象。在聲屏障的外側，反射聲波與入射聲波疊加，在聲場的局部區域內出現極值區域，水平方向距聲源12～13 m的區域內聲屏障的插入損失出現極大值，距聲源22～24 m的區域內聲屏障的插入損失出現極小值。

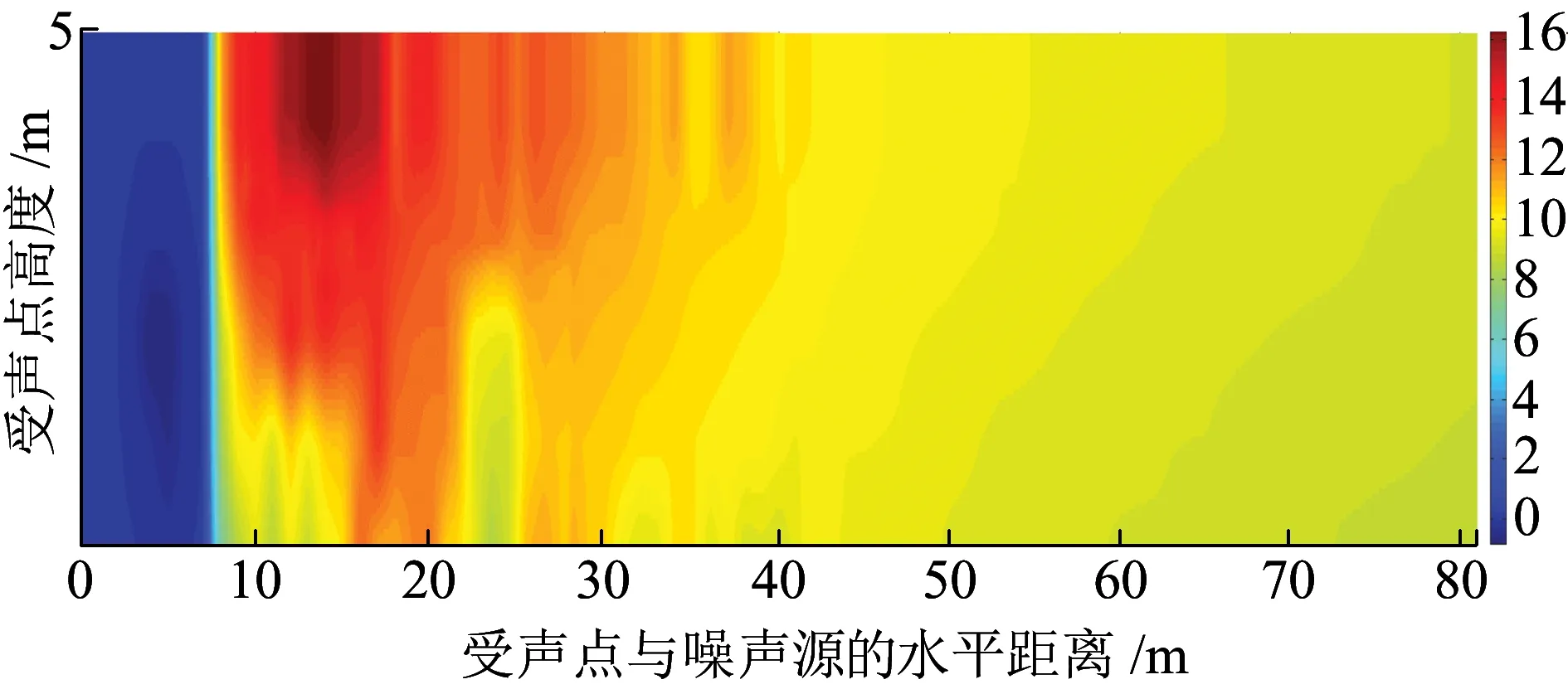
圖8 高度2.8 m的吸聲型聲屏障插入損失(單位：dB)

3.3 復合型聲屏障的組合形式

按聲波在聲場中的傳播類型可分為隔聲型聲屏障、吸聲型聲屏障及吸聲與隔聲相結合的復合型聲屏障。因其組合形式的不同，聲屏障的插入損失LIL及聲功率插入損失LIW也有差異，故擬運用遺傳算法及聲屏障邊界元理論優化聲屏障組合形式。

3.3.1 建立優化模型

由于復合型聲屏障的組合形式僅與聲屏障的安裝工程有關，而安裝工程的成本由固定聲屏障框架的成本Cf和兩種材料連接處的連接成本Cc組成，即

(11)

式中：q為連接處的個數；c為單個連接處的成本；m為固定框架成本向單個連接成本的轉化率，依據工程實際情況m一般取20～25。

將聲屏障的效益價值比Br作為優化模型的目標函數Z，即

(12)

3.3.2 編碼

選取泡沫混凝土作為復合型聲屏障的吸聲材料，其性能參數見表2；選取中空隔音玻璃作為復合型聲屏障的隔聲材料，其性能參數見表3。

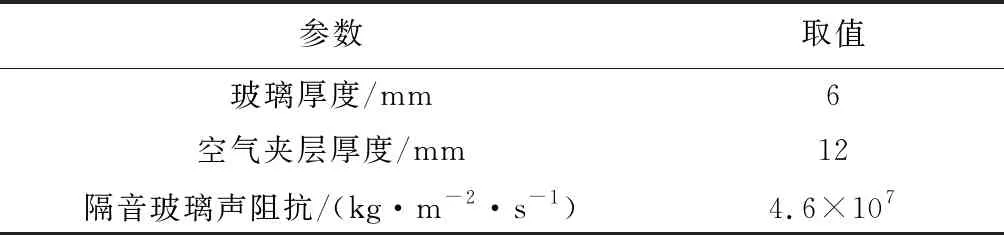
表3 中空隔音玻璃的性能參數

將高度為2.8 m的聲屏障結構體，離散為28個高度0.1 m的單元體，對每個單元體進行二進制編碼(“0”表示吸聲材料，“1”表示隔聲材料)，兩個不同材料的單元體連接時產生連接成本c。

3.3.3 遺傳優化

基于遺傳算法優化模型的基本操作，選取種群數量N=100、交換概率Pc=0.6、變異概率Pm=0.1的參數組合，結合聲屏障邊界元理論，運用MATLAB程序語言對目標函數進行優化。

目標函數優化編碼結果為00000011-11111111111111000000，即上部與下部均為高度0.6 m的泡沫混凝土，中部為高度1.6 m的隔音玻璃；聲功率插入損失LIW=3.296 3×10-8W。復合型聲屏障的插入損失LIL在場點內的分布如圖9所示，與吸聲型聲屏障相比，復合型聲屏障在聲屏障內側和外側均出現插入損失極值區域，尤其在聲屏障的內側還出現插入損失負值的區域。由于隔聲屏障的反射，反射波與入射波疊加，聲場內形成大量的干涉區域，從而出現大量的插入損失極值區域；在聲屏障內側，聲波在傳遞過程中的能量損失少，干涉現象明顯，因此出現插入損失負值。由于吸聲型聲屏障對低頻率聲波的降噪效果不佳，而復合型屏障同時擁有吸聲和隔聲兩種材料，能有效地減弱低頻聲波的繞射，故復合型聲屏障的降噪效果優于吸聲型聲屏障，其插入損失比吸聲型聲屏障高2.1 dB。

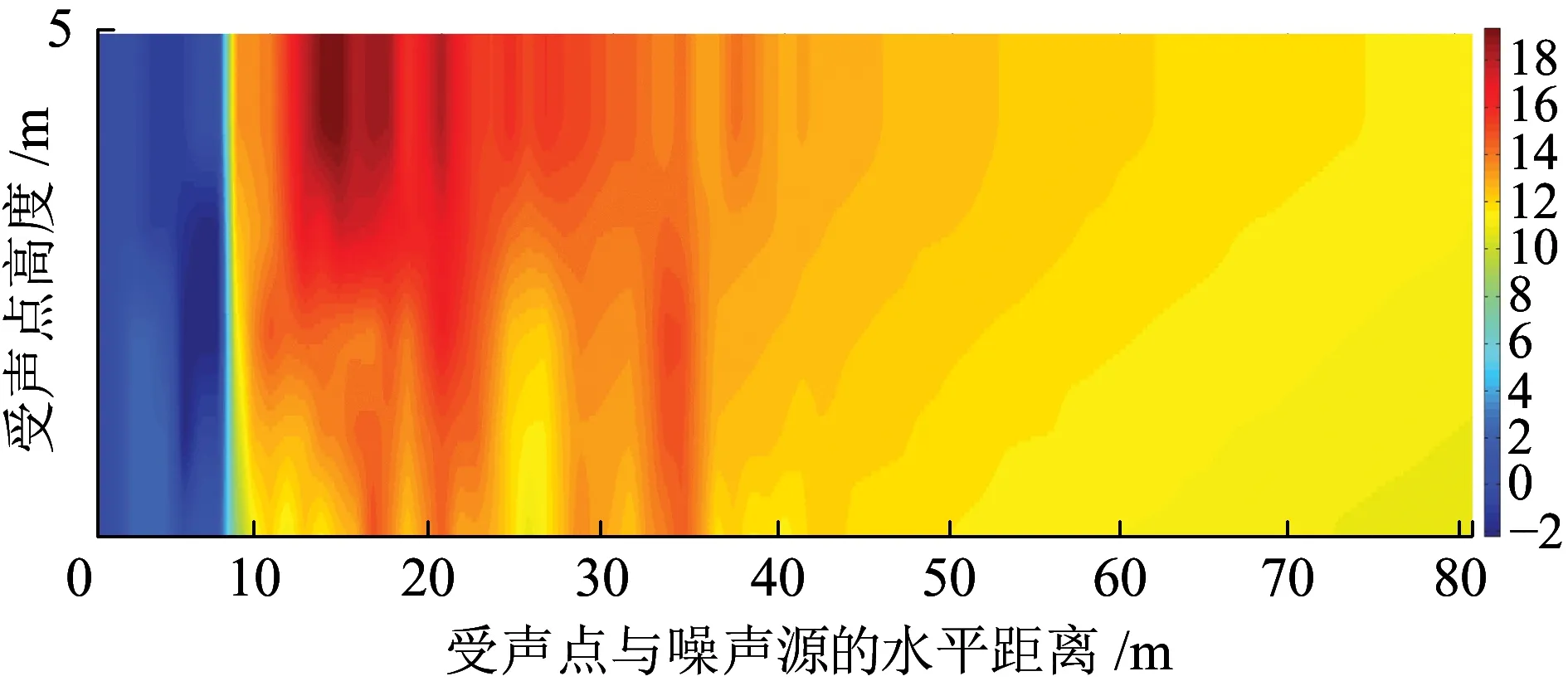
圖9 復合型聲屏障插入損失(單位：dB)

3.4 聲屏障頂端結構類型

聲屏障的頂端結構類型主要有：直壁型、折壁型、全封閉型及半封閉型。降噪要求較低的鐵路、公路主要選用直壁型聲屏障；折壁型聲屏障一般用于對聲屏障高度有限制且降噪要求較高的鐵路、公路；對于降噪要求高的高速公路及高架橋可選用全封閉型及半封閉型聲屏障；由于高速鐵路列車的速度是高速公路汽車速度的2～3倍，故一般高速鐵路極少采用全封閉型聲屏障。基于泡沫混凝土塑形效果好的優點，結合交通噪聲的頻譜特性，聲屏障頂端結構類型擬選用由泡沫混凝土塑形的折壁型頂端結構。考慮到泡沫混凝土抗拉強度低的特點，頂端結構不宜選用Y形、圓弧形等折壁形式，故選取T形及T形拓展型作為頂端結構類型，如圖10所示。

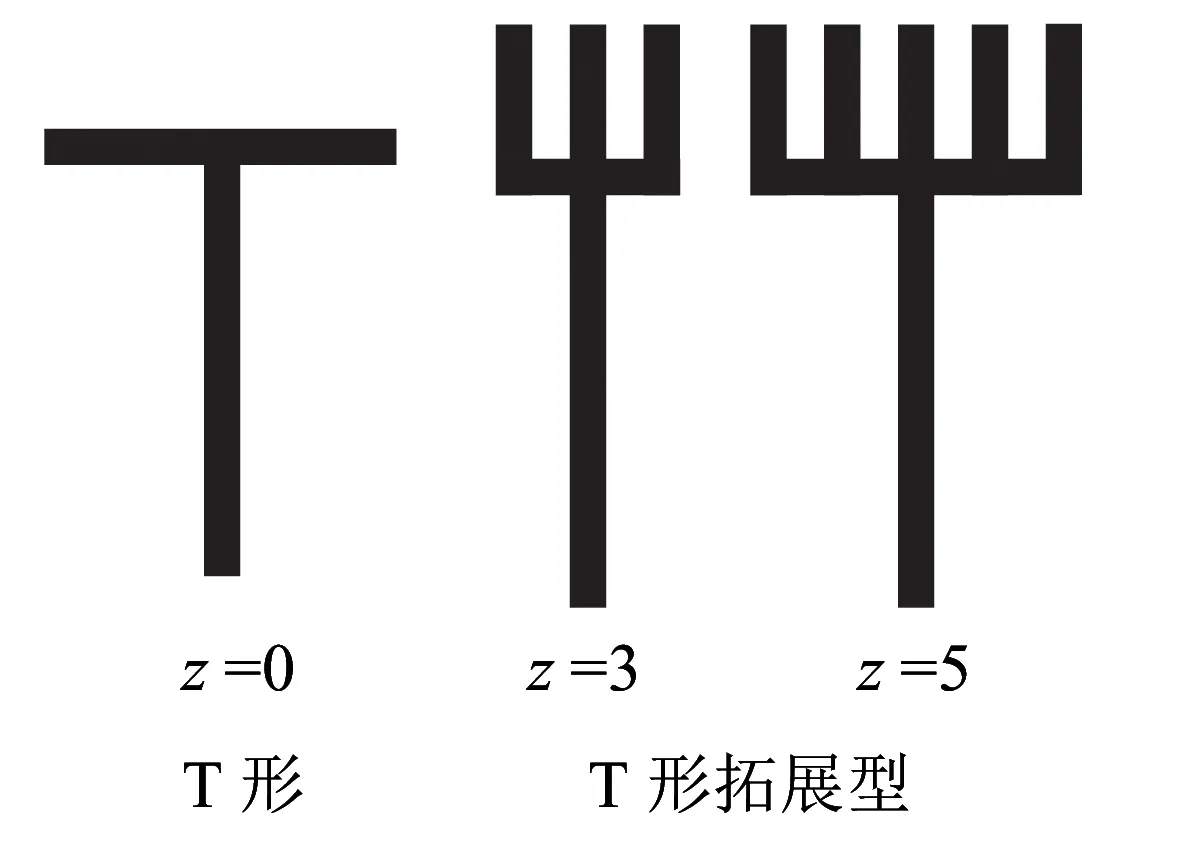
圖10 T形頂端結構

3.4.1 優化模型及編碼

考慮混凝土力學特性，選取5階(z=5)T形頂端結構作為聲屏障頂端結構的研究對象，其結構示意圖如圖11所示，頂部結構底板及T形翼均選用5 cm厚泡沫混凝土，T形翼之間空氣部分的厚度為5 cm，T形翼的高度為hi,hi=0～50 cm。

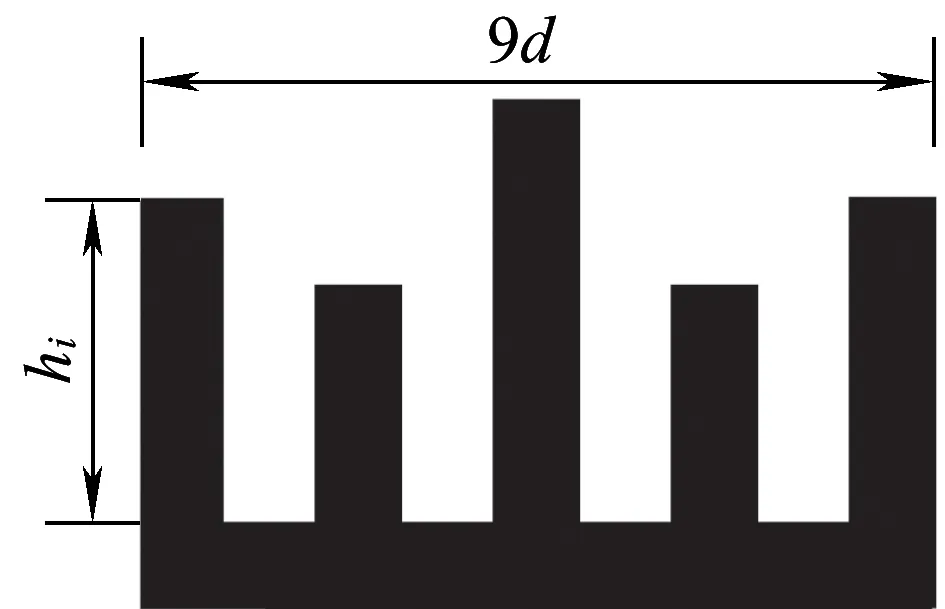
圖11 5階T形聲屏障頂端結構

聲屏障頂端結構成本主要由塑形泡沫混凝土的模板組成，故其優化模型為

(13)

對5個T形翼進行離散，離散為25個0.1 m的單元體，將每個單元體作為一個二進制碼(“0”表示空氣，“1”表示泡沫混凝土)。

3.4.2 遺傳優化

選取種群數量N=100、交換概率Pc=0.6及變異概率Pm=0.1的參數組合，考慮到混凝土施工的連續性，在評價種群內個體適應度前對種群進行前處理，即T形翼的混凝土單元體是連續的。結合聲屏障邊界元理論運用MATLAB程序語言對目標函數進行優化。

目標函數優化編碼結果為11100|10000|11110|11000|10000，T形翼的高度依次為15、5、20、10、5 cm。聲功率插入損失LIW=3.971 4×10-8W。由編碼結果可知，聲波在T形翼之間的空氣槽中進行多次反射，入射聲波的能量被消耗，T形翼聲屏障的降噪效果優于T形聲屏障；T形翼階數越高、分布越合理，降噪效果越好，故5階T形翼聲屏障的降噪效果優于3階T形翼聲屏障和T形聲屏障。T形頂端結構聲屏障的插入損失LIL在場點內的分布如圖12所示，T形折壁型聲屏障降噪效果優于直壁型，其插入損失比直壁型高1.1 dB，這是因為折壁型聲屏障的頂部結構既增大了吸聲屏障的面積，又增大了聲波繞射的路程。

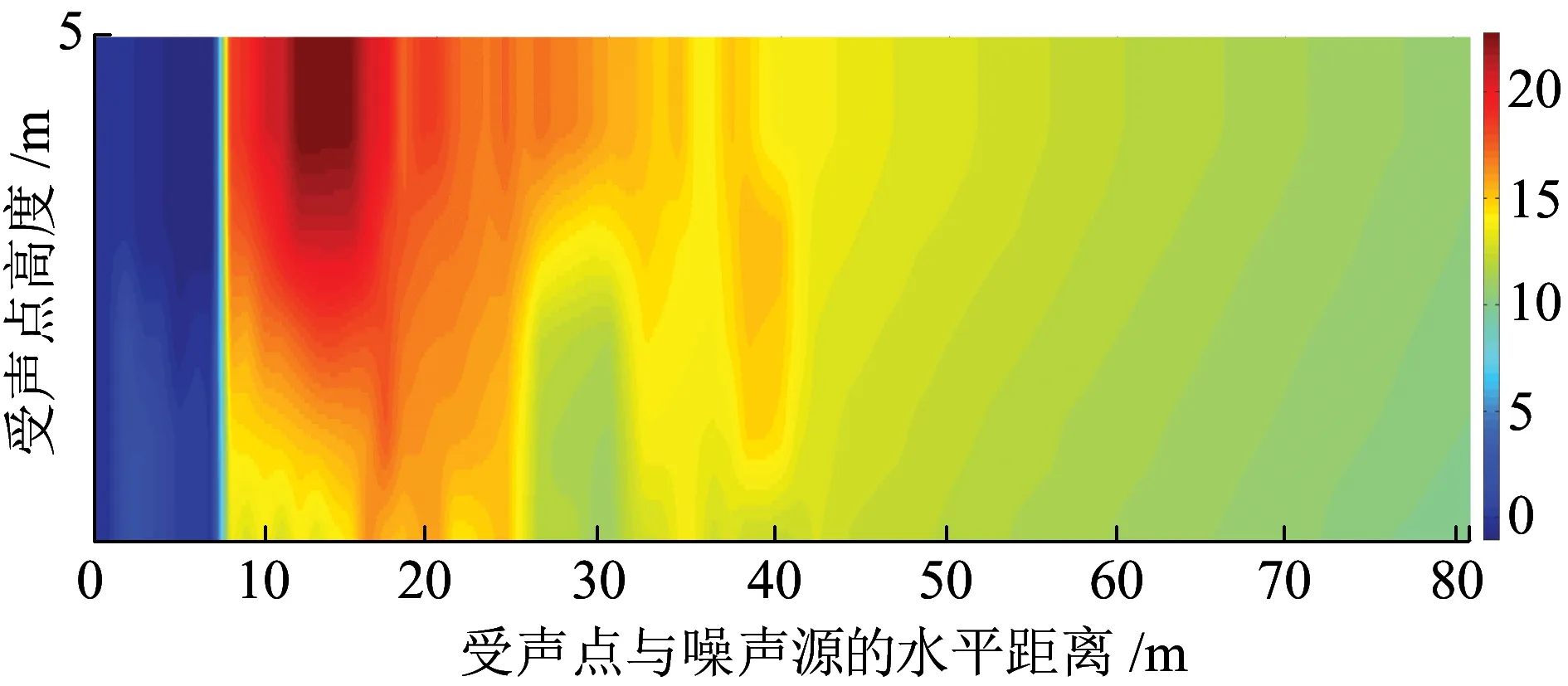
圖12 T形頂端結構聲屏障的插入損失(單位：dB)

4 模型試驗

基于遺傳算法、聲屏障邊界元理論及成本效益分析法優化聲屏障的結構形式，結合文獻[19]對優化的聲屏障結構在空曠的野外進行模型試驗。同時對實測數據與理論分析結果進行對比，驗證理論分析的正確性。

4.1 試驗材料與儀器

基于優化的聲屏障結構形式，選取泡沫混凝土作為聲屏障的吸聲材料，選取中空隔音玻璃作為復合型聲屏障的隔聲材料，其生產廠家及規格見表4。

表4 材料規格及廠家

注：A06表示泡沫混凝土的干密度為600 kg/m3；6+12+6表示兩邊玻璃厚度為6mm，玻璃中距為12 mm；泡沫混凝土板的厚度為5 cm。

聲屏障插入損失的測試采用文獻[19]中的方法。試驗聲源儀器裝置采用十二面體無指向聲源、音頻功率放大器、噪聲信號發生器及聲級計，其生產廠家及型號見表5，試驗儀器連接如圖13所示。

表5 試驗儀器及廠家

圖13 試驗聲源裝置

4.2 試驗方法

考慮到現場試驗環境的等效性，選取學校某處空曠場地進行聲屏障插入損失室外模型試驗。試驗前期對現場進行背景噪聲的測試，測試結果：背景噪聲的A計權聲壓級為48.6 dB(A)。連接儀器，調節十二面體無指向聲源的高度至0.5 m，播放白噪聲，調節音頻功率放大器的聲功率，使得在聲源正前方1 m處A計權聲壓級保持在(85±1)dB(A)。

本試驗采用雙向四車道的公路模型、高度為2.8 m且長度為5 m的雙側聲屏障，單獨放置的聲屏障如圖14所示。依據文獻[19]的規定，在滿足聲源及環境等效性的條件下，聲屏障插入損失應同時對受聲點和參考點進行測量，參考點的位置在聲屏障正上方距聲屏障頂端1.8 m，單側受聲點的位置如圖15所示。結合聲源的時間特性和聲源的聲級起伏變化，本次試驗的測量采樣時間為2 min，每個測點測量3次。

圖14 聲屏障模型

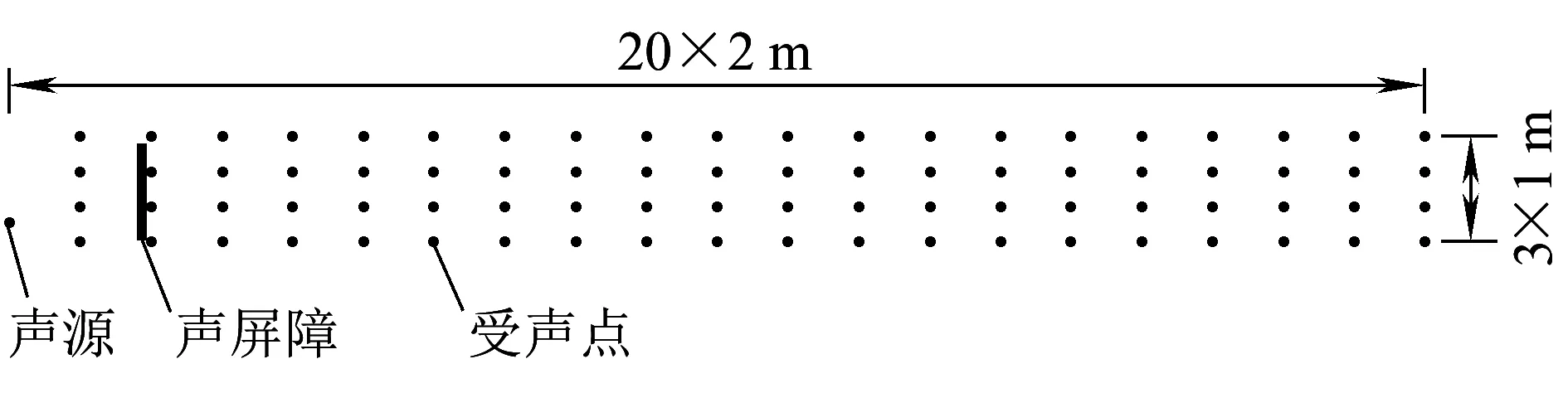
圖15 單側受聲點的布置

結合聲屏障插入損失的測試條件，其測試方法選用A計權直接測量法，聲屏障插入損失計算式為

LIL=(Lref,a-Lref,b)-(Lr,a-Lr,b)

(14)

式中：Lref,a為參考點處安裝聲屏障后的聲級，dB(A)；Lref,b為參考點處安裝聲屏障前的聲級，dB(A)；Lr,a為受聲點處安裝聲屏障后的聲級，dB(A)；Lr,b為受聲點處安裝聲屏障前的聲級，dB(A)。

結合MATLAB程序和實測的聲壓級數據對聲屏障聲場內部進行插值處理，并求解其聲場分布。對比復合型聲屏障插入損失的實測結果和理論結果，結合插入損失最大差值ΔLmax和插入損失波動率LSL進行誤差分析，驗證理論的正確性。

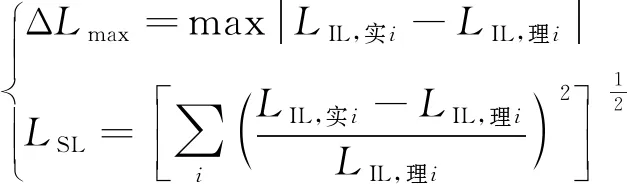
(15)

4.3 試驗結果分析

4.3.1 聲屏障組合形式的模型試驗

基于遺傳算法、聲屏障邊界元理論及成本效益分析法對聲屏障的組合形式進行優化，將優化后的聲屏障組合形式作為模型試驗的組合形式，現場測試圖如圖16所示。

圖16 聲屏障組合形式現場測試

結合復合型聲屏障插入損失的實測結果(圖17)和理論結果(圖18)分析可知，實測插入損失的分布規律與理論插入損失的分布規律一致，但場點的插入損失值存在一定的差距，這是由于環境誤差、材料誤差、試驗誤差、儀器誤差以及其他因素的誤差疊加導致的。插入損失最大差值ΔLmax為1.3 dB(A)，即實測插入損失偏離理論插入損失最大值為1.3 dB(A)；插入損失波動率LSL為1.89%，即實測插入損失偏離理論插入損失的離散程度為1.89%。插入損失的偏離程度和離散程度均在誤差允許范圍內，故可運用遺傳算法、聲學理論、邊界元理論及成本效益分析法對聲屏障的聲學環境進行模擬分析。

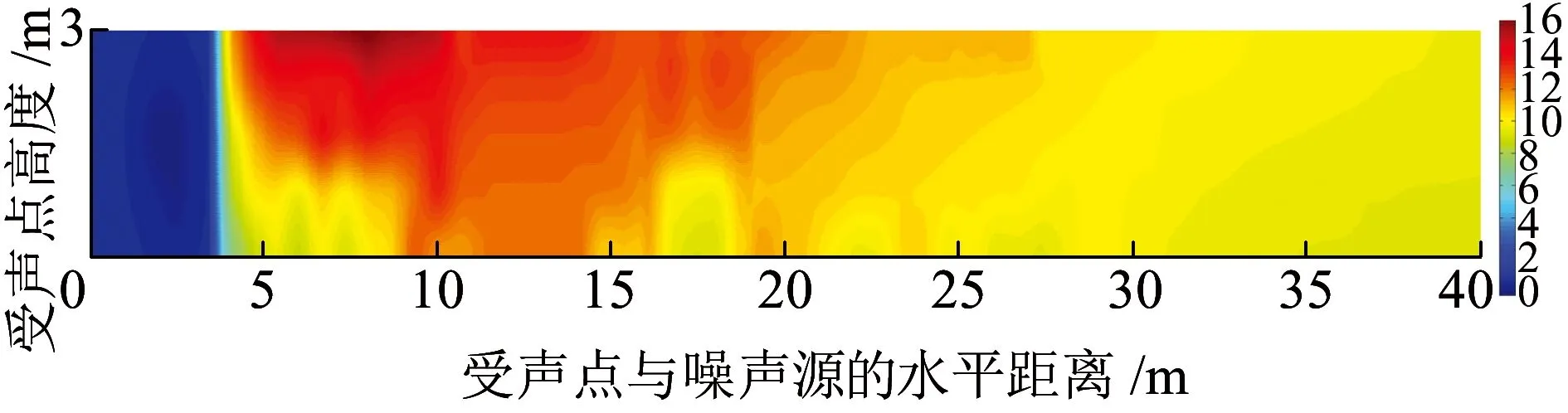
圖17 復合型聲屏障插入損失的實測結果(單位：dB)

圖18 復合型聲屏障插入損失的理論結果(單位：dB)

4.3.2 聲屏障頂端結構的模型試驗

基于遺傳算法、聲屏障邊界元理論及成本效益分析法對聲屏障的頂端結構進行優化，選取優化后的聲屏障頂端結構作為模型試驗的組合形式，現場測試如圖19所示。

圖19 T形頂端結構聲屏障的現場測試

結合T形聲屏障插入損失的實測結果(圖20)和理論結果(圖21)分析可知，實測插入損失的分布規律與理論插入損失的分布規律基本一致，但場點的插入損失值依然存在一定的差距。插入損失最大差值ΔLmax為1.6 dB(A)，即實測插入損失偏離理論插入損失最大值為1.6 dB(A)；插入損失波動率SL為2.28%，即實測插入損失偏離理論插入損失的離散程度為2.28%。插入損失的偏離程度和離散程度均在誤差允許范圍內，故可運用遺傳算法、聲學理論、邊界元理論及成本效益分析法對聲屏障的聲學環境進行模擬分析。

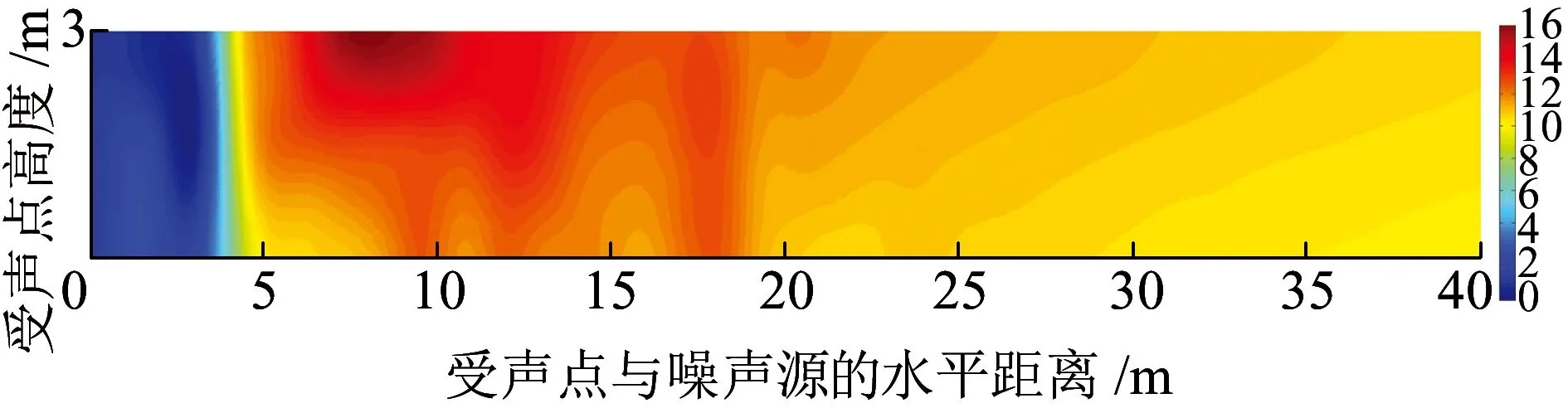
圖20 T形聲屏障插入損失的實測結果(單位：dB)

圖21 T形聲屏障插入損失的理論結果(單位：dB)

5 結論

基于遺傳算法、聲屏障邊界元理論及成本效益分析法，針對高速鐵路及高速公路的交通噪聲，優化聲屏障的高度、組合形式及頂端結構類型，并對試驗結果進行分析，得到以下結論：

(1)隨著聲屏障高度的增加，聲功率插入損失增加且增加趨勢趨于平緩，聲屏障的效益價值比先增加后減小，當聲屏障高度達到2.8 m時，聲屏障效益價值比達到最大；在聲屏障內側，聲屏障插入損失幾乎為0，在聲屏障外側，聲屏障插入損失存在極值區域。

(2)組合形式為0.6 m泡沫混凝土+1.6 m隔音玻璃+0.6 m泡沫混凝土的復合型聲屏障降噪效果優于其他復合型聲屏障，其插入損失比吸聲型聲屏障高2 dB(A)；復合型聲屏障在聲屏障內外側均出現插入損失極值區域，在其內側出現插入損失負值區域。

(3)T形折壁型聲屏障降噪效果優于直壁型聲屏障，其插入損失比直壁型聲屏障高1.1 dB(A)；5階T形翼聲屏障的降噪效果優于3階T形翼聲屏障和T形聲屏障。

(4)以高等級公路的交通噪聲為研究對象，聲屏障的優化模型為：上部與下部為0.6 m泡沫混凝土、中部為1.6 m中空隔音玻璃；頂部T形翼的高度依次為15、5、20、10、5 cm。

(5)聲屏障實測插入損失的分布規律與理論插入損失的分布規律基本一致。與理論插入損失相比，復合型聲屏障實測插入損失偏離理論最大值1.3 dB(A)，離散程度為1.89%；T形聲屏障實測插入損失偏離理論最大值1.6 dB(A)，離散程度為2.28%，且均在誤差允許范圍內。