結合空間信息選取最優端元組合的混合像元分解

徐 君，王彩玲

(1. 西安航空學院電子工程學院，陜西 西安 710077; 2. 西安石油大學計算機學院，陜西 西安 710065)

高光譜圖像雖然具有很高的光譜分辨率，但空間分辨率卻普遍不高，這就導致高光譜圖像中的每個像元可能不僅包含一種地物，而是多種地物覆蓋類型的混合。對于這種光譜混合像元，無法根據提取的光譜特性判斷其物質屬性，也不能在分類過程中簡單地將其歸于某一類地物。混合像元在高光譜圖像中的普遍存在使得傳統的像元級圖像分類和分割精度難以提高，是高光譜遙感技術向定量化方向發展的嚴重障礙。混合像元分解是解決該問題的有效方法，它能夠在亞像元尺度上獲取像元內部地物分布的真實信息，提高圖像分類的精度。

根據混合像元的產生機理，高光譜圖像混合模型可以分為線性混合和非線性混合兩種模型。在傳統的線性光譜混合像元分解算法中，一般假設圖像中的像元都包含全部的端元光譜，對每個端元給出一個對應的豐度估計，但這往往與實際情況并不相符[1-4]。

實際上混合像元并不一定包含所有端元，而是由其中的一小部分端元混合而成，即混合像元只包含一個端元子集。混合像元中實際所包含的端元也互不相同，因此混合像元所包含的端元是可變的。常用的線性混合模型在混合像元分解過程中將所有的端元都納入考慮范圍，對每個端元向量都進行豐度估計，因此存在過擬合的分解誤差。為了解決混合像元端元可變問題，國內外一些學者對如何選擇混合像元的最優端元子集作了一些研究。國外學者主要提出了多端元光譜混合分析(MESMA)[5-6]、迭代光譜混合分析(ISMA)[7]和端元可變線性混合模型(EVLMM)[8]等最優端元子集選擇方法。MESMA算法從光譜庫中選擇端元，假設每個像元最多由3個端元混合，嘗試對所有端元的組合進行光譜分解，運算效率較低，光譜分解的誤差較大。ISMA采用迭代算法去除豐度最小的端元，采用非限制性光譜分解方法進行豐度估計，根據混合像元光譜與剩余端元重建光譜之間均方根誤差RMSE的變化情況確定最優端元子集。EVLMM基于端元組合數量由少到多進行搜索，直到采用更多的端元進行光譜重建后所得RMSE比上一步大時停止。文獻[9]提出的OESSA算法首先利用所有端元進行非限制性光譜分解，然后根據豐度值量化重要程度的大小，對端元進行排序，由豐度最大的端元開始，逐漸增加端元個數解混，根據RMSE的統計結果確定最優端元子集。文獻[10]提出了一種端元子集的局域確定方法，首先利用所有端元對混合像元進行分解，根據該像元鄰域內各端元的豐度分布狀況直接判定是否為純像元，如果不是純像元，則根據鄰域內端元的豐度累加值大小排序，去掉累加值最小的端元，進行精度更高的二次解混。混合像元的端元可變性在實際中對應于混合像元的豐度矩陣具有稀疏特性。文獻[11—15]嘗試把稀疏原理與高光譜混合像元分解相結合，提出了基于稀疏約束的混合像元分解算法，基于稀疏約束的混合像元分解算法是在已知一個過完備的光譜庫的情況下，尋找方程的最簡單的解。

以上方法從不同思路對混合像元的可變性進行了研究，但實際上混合像元一般分布于不同地物的交界地帶，不同地物交界處的混合像元所包含的端元最有可能與周圍的地物分布狀況相關。針對這種情況，本文提出一種利用圖像的空間信息選取最優端元組合的混合像元分解方法，在混合像元周圍局部鄰域提取純凈像元光譜，與從整幅圖像中提取到的全部端元進行對比，根據分解后RMSE的變化情況優化端元組合，對混合像元進行分解，從而獲得最佳的光譜分解結果。

1 理論基礎

1.1 線性混合模型

線性混合模型(如圖1所示)是假定混合像元光譜由各端元的光譜通過線性疊加混合而成，由于其原理簡單，物理含義明確，運算效率高，分解精度基本滿足實際應用的需求，因而獲得了廣泛的應用。

圖1形象地闡述了線性光譜混合過程，在地面的3種物質分別為a1、a2和a3，所占面積的比例分別為s1、s2和s3，陽光照射在這3種地物上，互不干擾，而在成像光譜儀上形成一個混合像素點，混合像元得到的反射率為x=a1s1+a2s2+a3s3，它是各個光譜特征的線性疊加。

線性光譜混合模型的數學表達式為

(1)

式中，x為混合像元的反射率；Ai為像元的第i個端元向量；si為該像元內第i個端元的反射率比例(即豐度)；E為模型誤差；p為端元數目。

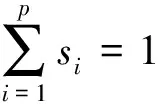
1.2 混合像元分解精度評價

對混合像元的分解結果所進行的評價分為定性評價和定量評價兩種。定性評價主要是通過目視的方式對分解后的端元分布豐度圖進行觀察，并與實際地物的分布狀況進行對比。為了對混合像元的分解結果進行準確客觀的評價，需要建立相關的評價指標進行定量評價，定量評價通過嚴格的數學計算分解，給出精確的對比評價結果，因而獲得了廣泛的應用。對真實高光譜圖像進行混合像元分解時，端元光譜和端元對應的豐度圖像信息一般是未知的，均方根誤差是一種比較簡單、常用的混合像元分解精度定量評價指標。

假設混合像元原始光譜向量為X，光譜分解所得的端元矩陣為A，豐度向量為S，則光譜重構后的光譜向量為

(2)

該像元的余差為

(3)

對于n維的光譜向量，均方根誤差為

(4)

式中,εj為余差向量中的元素。獲得的RMSE值越小說明算法的混合像元分解精度越高，算法越有效。

2 光譜分解誤差隨端元子集變化情況

現有的研究表明，利用圖像中的所有端元對混合像元進行分解，得到各端元的豐度值，然后從豐度最大的端元開始，按照豐度從大到小的順序，逐漸添加端元，建立并擴充端元子集，用這些端元子集分別對該混合像元進行二次分解，則混合像元分解的誤差總體上趨于減小[9]。

如對于整幅圖像包含10個端元、實際上由3個端元組成的混合像元，圖2給出了RMSE隨端元子集中端元數目增加的變化趨勢。

在混合像元分解時，如果端元子集中漏選實際存在的端元，那么光譜重構圖像與原始圖像的RMSE會很大；當端元子集中恰好包含實際存在的端元時，RMSE最小；而當端元子集中多選了冗余端元進行分解時為無偏估計，RMSE變化很小。

圖2中，按照豐度排序，在利用其中3個豐度最大的端元進行混合像元二次分解后，相比上一步2個端元分解時重構光譜與原始光譜之間的RMSE急劇下降，再向端元子集中增加端元數量進行分解，RMSE的變化也不大，而是趨于平緩，由此可以判斷曲線“拐點”對應的端元集就可以作為組成該混合像元的最優端元子集，該混合像元實際包含的端元數為3。

3 結合圖像空間信息的最優端元子集選擇

當圖像中地物種類較多、存在較多端元的時候，如果通過全局搜索的方式在全部端元中搜索混合像元的最優端元組合效率較低，因自然界地物往往具有一定的空間結構，如農田、森林、草地、建筑物，湖泊等，這些不同種類地物區塊之間光譜差異明顯。光譜混合像元一般位于地物區塊的邊緣交界地帶，在混合像元的周圍存在純凈像元的可能性較大，而這些純凈像元的光譜往往就是組成混合像元的端元光譜。充分利用圖像的空間信息，從混合像元的就近鄰域開始尋找純凈像元，搜索確定混合像元的最優端元組合，可以提高搜尋混合像元最優端元子集的效率。如圖3所示，本文提出一種結合圖像的空間信息尋找混合像元最優端元子集的方法。具體步驟如下：

(1) 定義一個結構元素K，K是一個中心像元坐標為(x,y)、邊長為k的正方形。讓結構元素K在圖像上滑動，在結構元素覆蓋的區域內計算所有像元光譜向量均值

(5)

計算結構元素覆蓋區域內k2個像元的光譜向量到均值光譜向量Ck的歐氏距離，記為dk。

(2) 根據凸面幾何學理論，最大dk對應的像元必然是結構元素覆蓋的局部區域內“最純”的像元，將其記為第1個“端元”e1；然后將結構元素k2個像元中距離e1最遠的像元記為第2個“端元”e2；距離e1和e2所構成直線最遠的像元(這個點向e1和e2所構成的直線作垂線距離最遠)記為第3個“端元”e3；距離e1、e2和e3所構成平面最遠的像元記為第4個“端元”e4；以此類推，最多得到k2個“端元”e1,e2,…,ek。

(3) 對步驟(2)中獲得的“端元”ei，與從整幅圖像中提取的所有端元ai(i=1,2,…,m)進行對比，計算它們之間的光譜夾角距離

(6)

如果光譜夾角SADi小于設定的閾值，光譜高度相似，則可以將對應的端元ai加入結構元素K覆蓋區域中心位置處混合像元的最優端元子集中。此步驟本質上是通過結構元素K在混合像元附近鄰域尋找“純像元”光譜作為混合像元的端元光譜，這符合混合像元一般位于地物區塊邊緣交界地帶的規律，實際上是利用了圖像的空間信息就近尋找混合像元的最優端元子集。

(4) 最優端元子集建立后，應用全限制線性混合模型對混合像元進行分解，然后計算重構光譜與原始光譜的RMSE。如果該RMSE近似等于全端元a1,a2,…,am分解時與原始光譜之間的RMSE，則當前的端元子集即為最優；如果該RMSE遠大于全端元a1,a2,…,am分解時的RMSE，則說明端元子集中缺少實際存在的端元。

(5) 增大結構元素K(x,y)的尺寸(增大邊長k)，擴大搜索范圍，返回步驟(1)重復執行，直到RMSE減小到近似全端元分解時的RMSE為止，最終得到混合像元的最優端元子集，進而得到最優的光譜分解結果。

圖3為擴大結構元素尋找最優端子集示意圖。圖3(a)中結構元素K1邊長為3，結構元素內只包含兩種物質的純像元，因此只能找出結構元素中心位置處混合像元(x,y)包含的兩個端元e1和e2；擴大結構元素，使其邊長為5(如圖3(b)所示)，結構元素內涵蓋3種物質的純像元，即可找到混合像元(x,y)的全部端元e1、e2和e3。

4 試驗與討論

4.1 模擬圖像試驗

在USGS[16]礦物光譜庫中選擇4種礦物光譜作為端元，其光譜曲線如圖4所示。

添加SNR=30 dB的高斯噪聲，構建大小為200×200的模擬圖像。如圖5所示， 模擬圖像4個角上分布著4個端元的純像元，陰影部分是由4種端元混合而成的混合像元。

以4個端元的其中一個進行分析，圖6為端元①的實際豐度圖及分別采用UCLS、FCLS、迭代光譜混合分析(ISMA)及本文所提出的端元可變混合像元分解方法解混后的豐度圖。圖中顏色由淺到深表示豐度逐漸增加。

試驗數據見表1，可以看出，UCLS由于沒有添加豐度約束條件，因而產生了最小的RMSE，由于對豐度和沒有進行約束，豐度和在0.95～1.05之間的像元僅占圖像中像元的69.35%；FCLS嚴格滿足和為1的約束條件，但RMSE較大，分解精度較低。ISMA算法的RMSE也比FCLS大。本文提出的算法在RMSE上優于ISMA算法，并且最后的分解結果豐度和滿足和為1的要求。

表1 模擬圖像試驗結果

4.2 真實數據試驗

美國內華達州Cuprite地區礦物品種多樣，各種礦物露頭良好，該地區的AVIRIS數據包含224個波段(0.4～2.5 μm)，空間分辨率和光譜分辨率分別為20 m和10 nm，適合檢驗混合像元分解算法的性能。去除其中受水蒸氣吸收影響較大和低信噪比的波段(1～3、104～113、148～167、221～224)，保留187個波段，經過輻射校正得到反射率數據，并選取其中200×200大小的區域用于試驗。圖7為該區域的假彩色合成圖與執行UCLS、FCLS ISMA及本文算法所得到的其中一個端元豐度的分布圖。

表2是對試驗所得結果的數據分析。結果表明，UCLS算法的RMES最小，但圖像中僅有11.8%的像元豐度和在0.8～1.2之間。FCLS算法雖然滿足豐度和為1的約束條件，但RMES最大。相比本文算法，ISMA算法的RMSE較大，豐度和也不滿足和為1的約束條件。本文方法在選定最優端元子集進行二次分解時，采用的是FCLS算法，豐度和為1。因此本文所提算法在性能上是優于ISMA的。

表2 AVIRIS數據試驗結果

本文方法利用圖像的空間信息，用結構元素搜索周圍鄰域的“純像元”光譜，優先組成最優端元子集，進行光譜分解。表2中真實高光譜數據的試驗結果再次表明，采用本文方法優化后的端元子集進行光譜分解結果在RMSE上優于FCLS和SALSA；且在二次分解時采用FCLS算法，因此豐度和為1，符合實際情況，總體上達到了較好的光譜分解效果。

5 結 語

混合像元分解是高光譜遙感信息提取的常用方法。傳統的分解方法一般假設混合像元包含圖像中的所有端元，但這并不符合實際情況，因此導致分解結果對噪聲敏感，分解精度不高。實際的混合像元只包含少數端元，由于地物空間分布上的連續性，混合像元所包含的端元往往與附近區域分布的地物有關。

本文結合圖像空間信息，用一個空間結構元素在混合像元附近區域就近確定選取最優端元子集。相比其他方法，該方法既不需要遍歷圖像中所有端元,且通過迭代運算來尋找最優端元子集，也不需要按照初次解混后的豐度大小進行排序后對端元進行取舍，而是將附近鄰域的“純像元”光譜優先加入最優端元子集，從最有可能屬于該混合像元的端元開始搜索添加，這符合現實地物分布的實際情況，有利于提高最優端元子集的搜索效率，最終獲得較好的分解效果。