水庫放空問題數(shù)值模擬研究

李 昂

（重慶市水利電力建筑勘測(cè)設(shè)計(jì)研究院，重慶 401120）

0 引言

水利工程中，為了滿足檢修、國防（如戰(zhàn)爭）或者緊急情況（例如地震）等要求，往往需要在水庫較低高程位置修建放空建筑物，如在重力壩或者拱壩壩身設(shè)置的放空底孔，在河岸開鑿的放水隧洞等。另外，水池放空、船閘充水及泄水等均需要計(jì)算放水及充水所需時(shí)間。

對(duì)于放空時(shí)間的確定，常通過如下方法進(jìn)行估算（見圖1）。

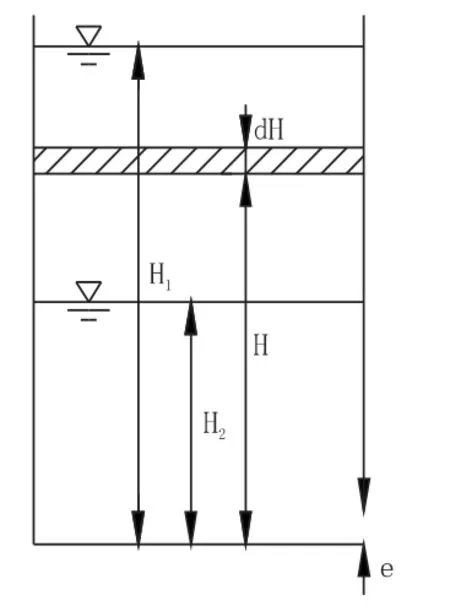
圖1 放空過程計(jì)算示意圖

為方便計(jì)算，假定上游無來流，孔口做自由出流，則dt 時(shí)段內(nèi)從孔口流出的水流體積與同一時(shí)段內(nèi)容器里面水體體積的減小量相等，即：

式中：Q 為孔口體積流率，A 為容器橫截面面積，H 為容器內(nèi)水深，μ 為孔口流量系數(shù)，b 為孔口寬度，e 為孔口高度，g 為重力加速度，取9.81 m/s2。

若孔口水頭從H1變化至H2，對(duì)（2）式進(jìn)行積分得到放空所需時(shí)間為：

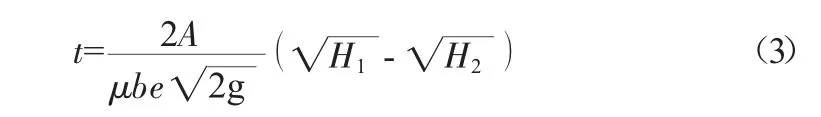
對(duì)于上述計(jì)算方法，有兩點(diǎn)不足：其一是計(jì)算過程中將孔口流量系數(shù)μ 假定為常值，這與實(shí)際情況不符，事實(shí)上，孔口流量系數(shù)不僅與孔口型式有關(guān)，還與作用水頭有關(guān)。通常情況下，隨著水頭的降低，流量系數(shù)也會(huì)逐漸減小，這就造成了計(jì)算得出的放空時(shí)間偏小。其二，式（1）中始終將孔口出流形式做閘孔出流考慮，其流量計(jì)算公式采用有壓流計(jì)算公式，然而當(dāng)水頭降至一定程度時(shí)，孔口出流形式將由閘孔出流變成堰流（即無壓流），此時(shí)上述計(jì)算過程已經(jīng)不再適用，需要采用無壓流計(jì)算公式對(duì)泄流量進(jìn)行計(jì)算。根據(jù)吳持恭的研究成果[1]，當(dāng)閘底坎為平頂堰的情況，下列數(shù)值可作為判別流態(tài)的大致界線：當(dāng)為閘孔出流；當(dāng)為堰流。

當(dāng)孔口出流形式為堰流時(shí)，其泄流時(shí)間計(jì)算過程如下（式中m 為孔口為堰流時(shí)的流量系數(shù)）：

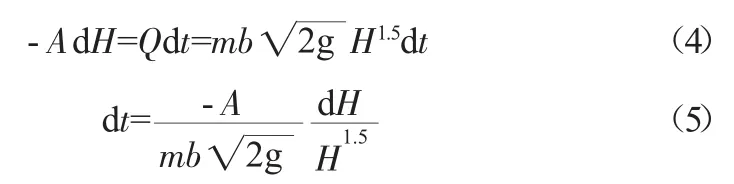
若孔口水頭從H3變化至H4，對(duì)上式進(jìn)行積分得到所需時(shí)間為：

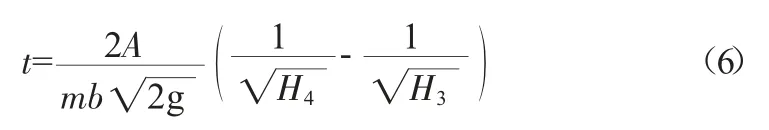
對(duì)于本文所述的放空問題，由于出流孔口長度為零，所以當(dāng)水頭變化至界限水位時(shí)，孔口出流流態(tài)將迅速由閘孔出流變?yōu)檠吡?。但是?shí)際工程問題中的放空建筑物往往是具有一定長度的有壓孔口，此時(shí)將出現(xiàn)兩個(gè)界限水位，即上界限水位與下界限水位，此二水位之間有壓管內(nèi)將表現(xiàn)為明滿流交替狀態(tài)，常規(guī)的計(jì)算方法不再適用。

另外，隨著水頭的降低，一些不利的水力現(xiàn)象也將可能出現(xiàn)，譬如前文提到的明滿交替流將對(duì)有壓管道的結(jié)構(gòu)穩(wěn)定造成不利影響，低水位情況常常出現(xiàn)的立軸漩渦也是一個(gè)需要重點(diǎn)關(guān)注的現(xiàn)象。這些現(xiàn)象在常規(guī)的計(jì)算過程中都是無法預(yù)測(cè)的，隨著計(jì)算機(jī)技術(shù)以及數(shù)值計(jì)算理論的飛速發(fā)展，數(shù)值模擬的方法為該問題的解答提供了一條較為經(jīng)濟(jì)可靠的解決方案。

對(duì)于非恒定流狀態(tài)下水庫放空問題的數(shù)值模擬計(jì)算目前還未見相關(guān)文獻(xiàn)，其計(jì)算精度是否能夠滿足要求也不得而知。本文分別通過二維和三維的計(jì)算模型對(duì)棱柱形容器自由出流進(jìn)行全時(shí)域過程的模擬，從而對(duì)數(shù)值模擬在放空問題上的應(yīng)用提供一些技術(shù)支撐。

1 數(shù)學(xué)模型

本文分別采用二維和三維RNG k-ε 雙方程模型對(duì)紊流進(jìn)行模擬，采用控制體積法來對(duì)偏微分方程進(jìn)行離散，采用SIMPLER 法對(duì)壓力和速度進(jìn)行耦合，邊墻采用無滑移邊界條件[2]，采用VOF 法[3]對(duì)自由面進(jìn)行捕捉。

本文采用的RNG k-ε 紊流模型，其連續(xù)方程，動(dòng)量方程和k，ε 方程可分別表示如下：

連續(xù)方程：

動(dòng)量方程：

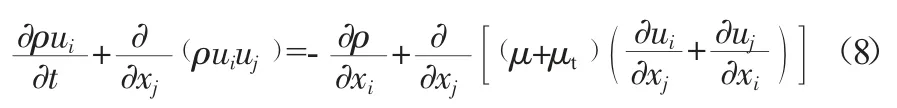
k 方程：

ε 方程：

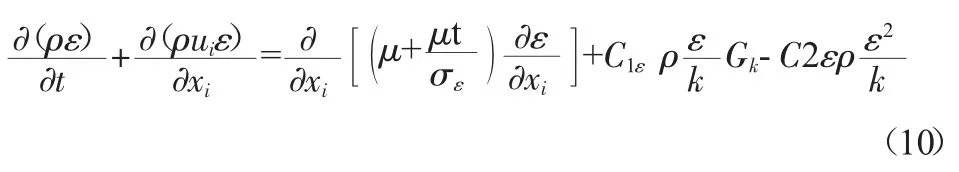
式中：ρ 和μ 別表示為體積分?jǐn)?shù)平均的密度和分子黏性系數(shù)，p表示修正壓力，μt表示紊動(dòng)黏性系數(shù)，它可以根據(jù)紊動(dòng)能k 及紊動(dòng)能耗散率ε 求解得出。

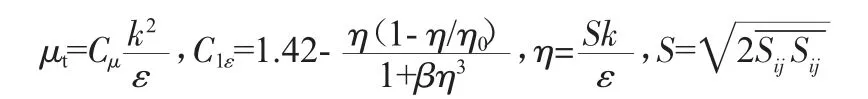
以上各個(gè)表達(dá)式中，i=1，2，3（對(duì)二維計(jì)算 i=1，2），即{xi=x,y,z},{ui=u,v,w}（對(duì)二維計(jì)算 {xi=x,y},{ui=u,v}）；j 表示求和下標(biāo)，方 程 中 通 用 模 型 常 數(shù)[4]η0=4.38,β=0.012,Cμ=0.0845,C2ε=1.68,σk=0.7179 和 σε=0.7179。

某水庫總庫容為1200 萬m3，死庫容110 萬m3，興利庫容1090 萬m3。放水洞尺寸為2 m×2 m（寬×高），水庫正常蓄水位時(shí)孔口水頭為30 m，其建模概化如下：

二維建模容器長 20 m（X 向），高 30 m（Y 向），孔口位于容器右下角，孔口高度2 m，網(wǎng)格間距0.1 m。三維建模容器長20 m（X 向），寬 20 m（Y 向），高 30 m（Z 向），孔口寬 2 m，高 2 m；網(wǎng)格整體間距為0.4 m，在孔口周圍（X=0～5 m;Y=-5 m～5 m；Z=0～8 m）進(jìn)行局部加密，加密后間距為0.2 m。設(shè)置模型頂部為壓力進(jìn)口，孔口為壓力出口。圖2 為三維模型布置圖。

圖2 三維計(jì)算模型布置圖

2 計(jì)算結(jié)果分析

圖3 為二維數(shù)值與三維數(shù)值計(jì)算的水位隨時(shí)間變化曲線及其與理論計(jì)算（按照式（3）進(jìn)行計(jì)算，流量系數(shù)其中ζ 為局部損失系數(shù)，取0.5，則孔口流量系數(shù)μ=0.816）的對(duì)比?？梢钥吹?，在開始時(shí)段，二維數(shù)值計(jì)算與三維數(shù)值計(jì)算均與理論計(jì)算具有較好的吻合度，這也驗(yàn)證了數(shù)值計(jì)算結(jié)果是可靠的、可信的；隨著水位的逐漸降低，數(shù)值解逐漸偏離理論計(jì)算結(jié)果，但是二者總體變化趨勢(shì)一致，分析認(rèn)為造成此種情況的原因是理論計(jì)算采用的流量系數(shù)是一個(gè)常值，而實(shí)質(zhì)上隨著水位的降低，孔口的流量系數(shù)也逐漸減小，故而同一時(shí)刻的水位數(shù)值計(jì)算結(jié)果比理論值偏大，二維數(shù)值計(jì)算與三維數(shù)值計(jì)算均具有類似的結(jié)果。

另外也可以觀察到，三維計(jì)算比二維計(jì)算具有更高的精度以及吻合度，根據(jù)前文對(duì)于孔口出流流態(tài)的判定條件可以計(jì)算得到界限水位H=e/0.65=2/0.65=3.08 m，從圖3（b）中可以看到三維數(shù)值計(jì)算結(jié)果近乎在界限水位附近才與理論計(jì)算結(jié)果逐漸出現(xiàn)相對(duì)較大的差異，而二維數(shù)值計(jì)算（圖3（a））則在比較高的水位條件下就開始出現(xiàn)偏離。使用均方根誤差（RMSE）來定性地分析數(shù)值計(jì)算結(jié)果的精度，其計(jì)算式如下：

式中：n 表示水深計(jì)算點(diǎn)個(gè)數(shù)，Htheoretical表示理論計(jì)算結(jié)果，Hnumerical表示數(shù)值計(jì)算結(jié)果，顯然RMSE 越小，則精度越高。計(jì)算得到二維數(shù)值計(jì)算RMSE 為1.17，而三維數(shù)值計(jì)算RMSE 為0.65，故而對(duì)于精度要求較高的放空情況，數(shù)值計(jì)算模型建議采用三維計(jì)算。

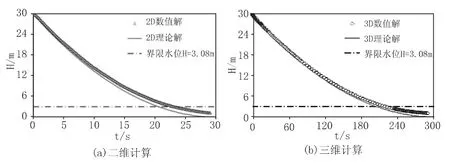
圖3 數(shù)值解與理論解對(duì)比

圖4 為孔口流量系數(shù)隨水位變化關(guān)系曲線，該圖直觀地顯示了孔口流量系數(shù)隨著庫水位的降低而減小，且水位降低越多，該趨勢(shì)越明顯，界限水位以上流量系數(shù)隨著水頭減小近似呈線性減小趨勢(shì)；當(dāng)水位降至界限水位后，孔口流量系數(shù)迅速減小，這是由于孔口流態(tài)變成堰流所致；另外，三維數(shù)值計(jì)算的流量系數(shù)比二維數(shù)值計(jì)算結(jié)果稍大，但是二者差異相對(duì)不大且變化規(guī)律一致。

圖5 為孔口單寬流量隨水位變化關(guān)系曲線，隨著庫水位的降低，單寬流量逐漸減小，當(dāng)水位降至界限水位以下后變化更為明顯，這同樣是因?yàn)榭卓诹鲬B(tài)的轉(zhuǎn)換所致；同樣地，三維數(shù)值計(jì)算的單寬流量比二維數(shù)值計(jì)算結(jié)果稍大。

圖4 流量系數(shù)隨水位變化關(guān)系

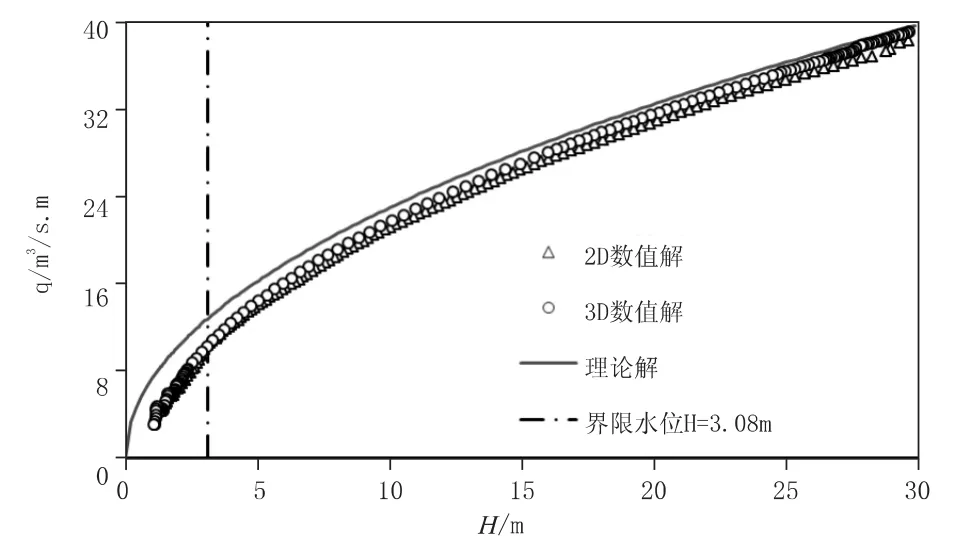
圖5 單寬流量隨水位變化關(guān)系

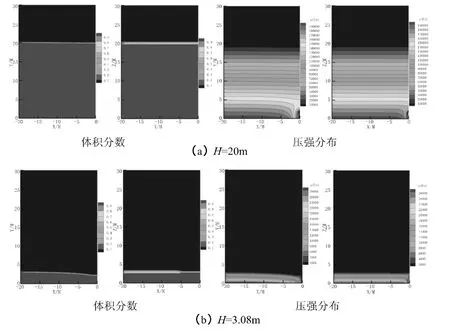
圖6 為不同典型水位條件下（H=20 m、H=3.08 m、H=1.5 m，分別表示閘孔出流、過渡流及堰流）容器內(nèi)水流體積分?jǐn)?shù)及壓強(qiáng)分布情況，其中左側(cè)為二維數(shù)值計(jì)算結(jié)果，右側(cè)為三維數(shù)值計(jì)算結(jié)果（取孔口中軸面，即Y=0 m 斷面）?？梢钥吹疆?dāng)水位較高（如圖7（a）所示）時(shí)，二維數(shù)值計(jì)算與三維數(shù)值計(jì)算結(jié)果幾乎沒有差異；隨著水位的降低，二者的差異逐漸趨于明顯，二維數(shù)值計(jì)算孔口上游影響區(qū)域較三維計(jì)算大，這主要是因?yàn)槿S計(jì)算橫向?qū)挾龋?0 m）遠(yuǎn)大于孔口寬度（2 m），故而孔口上游附近區(qū)域的流速迅速減小，從而造成水面降低沒有二維計(jì)算那么明顯。

為了簡化計(jì)算，建模模型完全對(duì)稱且孔口沒有長度，故而在全時(shí)域過程中不會(huì)出現(xiàn)明滿交替流，同時(shí)也沒有觀察到立軸漩渦的產(chǎn)生。但是對(duì)于實(shí)際工程問題，出流孔口往往具有一定長度，在水位逐漸下降的過程中，不可避免地會(huì)遇到明滿交替流以及立軸漩渦的產(chǎn)生，此種情況通過常規(guī)的物理模型試驗(yàn)往往很難實(shí)現(xiàn)全時(shí)域過程的模擬，此時(shí)數(shù)值計(jì)算的優(yōu)勢(shì)將顯現(xiàn)無遺。

另外可以觀察到，即使是在非常低的水位條件下，容器最左側(cè)壁面（X=-20 m）附近水面也基本保持水平，且各水位條件下該區(qū)域壓強(qiáng)近似呈靜水壓強(qiáng)分布，即該區(qū)域行進(jìn)流速幾乎為零。事實(shí)上，計(jì)算過程中選取的容器內(nèi)水深就處于該位置，這表明模型的建模長度滿足要求，容器水位的讀?。ㄓ捎谒畾饨唤缑婢哂幸欢ǖ母叨?，計(jì)算中選取水相體積分?jǐn)?shù)為0.5 的高程位置作為容器內(nèi)水深）不需要考慮行進(jìn)流速的影響。

圖6 2D 與3D 數(shù)值計(jì)算水力參數(shù)對(duì)比

3 結(jié)果與討論

本文針對(duì)實(shí)際工程中可能遇到的放空問題，將問題進(jìn)行簡化后分別進(jìn)行了二維和三維數(shù)值計(jì)算，結(jié)果表明：

1）運(yùn)用數(shù)值計(jì)算的方法來模擬非恒定條件下的放空問題是可行的，二維與三維數(shù)值計(jì)算結(jié)果均與理論分析結(jié)果具有相對(duì)良好的吻合度，但是三維數(shù)值計(jì)算結(jié)果的計(jì)算精度要優(yōu)于二維計(jì)算，對(duì)于精度要求較高的實(shí)際問題，建議采用三維數(shù)值計(jì)算。

2）當(dāng)水位降至界限水位以下后，數(shù)值計(jì)算結(jié)果與理論計(jì)算結(jié)果出現(xiàn)較大差異，這主要是因?yàn)榭卓诔隽黝愋陀砷l孔出流向堰流的轉(zhuǎn)換所致，這與理論分析的結(jié)論一致，數(shù)值計(jì)算較好地驗(yàn)證了這一現(xiàn)象。

3）由于三維數(shù)值計(jì)算考慮了容器寬度的影響，孔口附近行進(jìn)流速比二維數(shù)值計(jì)算結(jié)果偏小，其速度和壓強(qiáng)受影響范圍也較小，這也是三維數(shù)值計(jì)算精度更高的主要原因。