無窮級數的柯西和與切薩羅和

趙小玲 上海電機學院 文理學院

無窮級數求和問題是級數教學中的一個起點，也是重點和難點。在《高等數學》中，首先定義了無窮級數的收斂和發散，接著才定義了收斂級數的和，這種和稱為柯西和。可以發現，此種定義框架下，發散級數是不能求和的。但是，當我們改變和的定義方式時，某些發散級數也能求和，且與柯西和是相容的。意大利數學家切薩羅就提出了另一種定義方式方式，讓我們可以求出某些發散的無窮級數的和。

一、柯西和

利用上述定義，即求部分和數列的斂散性，我們可以得到級數的斂散性，并求出收斂級數的和。

例1：用柯西和定義討論下列級數的和。

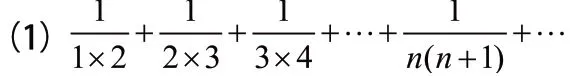
（2）1-1+1-1+…+(-1)n-1+…

（3）1+2+3+4+…+n+…

解：(1) 因為級數的前n 項的部分和

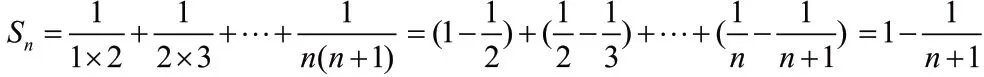
在判斷級數收斂或發散時，我們還特別強調了如下一些性質。

（1）收斂級數的逐項和構成的新級數仍然收斂；發散級數的逐項和構成的新級數不一定發散；如果兩級數逐項和的新級數發散，原級數中至少有一個發散；如果兩級數逐項和的新級數收斂，原級數不一定都收斂。

（2）在級數中增加或減少有限項不改變級數的斂散性；但在收斂時，級數的和數不同的；

（3）在收斂級數上任意加括號構成的級數仍然收斂，且和不變；若加括號構成的級數發散，則原級數一定發散；若加括號構成的級數收斂，原級數不一定收斂（即不能用加括號改變級數運算順序的方法求級數的和）。 在第三個性質中，著重強調了發散級數求和不能任意加括號。例如是發散的，但是在給此級數用不同的方法加括號以后有：這兩個加括號后改變運算順序的級數均是收斂的，但收斂到不同的數值。表明用任意加括號的方法求級數的和并不科學。

那么，對于發散級數，有沒有一種方法可以更好地描繪級數趨近于哪一個常數呢。比如格蘭迪級數，它的和一直在0 和1 之間擺動，我們直觀上認為，它應該趨近于二分之一比較合理。事實上，用切薩羅求和，確實可以得到這樣的結論。

二、切薩羅和

例如：用切薩羅和定義討論例1 中各級數的和。

解：(1) 因為級數的前n 項的部分和

所以級數和為1。可見，此定義方式與柯西和是相容的，即柯西和若存在，則切薩羅和也存在且與柯西和相等。

當然，切薩羅和也不是萬能的，對于（3）這個全體自然數相加的發散級數，用切薩羅定義不能求出它的和。

從以上例子可以看出，在研究無窮級數求和的發展過程中有著很多數學理論上的跳躍式發展。全體自然數相加的級數，用切薩羅定義不能求出它的和，但是用拉馬努金和的定義方式可以得到一個令人瞠目結舌的 “和”。我們在數學的學習過程中要特別注意數學思維的培養，注意數學架構的嚴謹清晰，有理有據。在一定的公理體系下，通過嚴密的邏輯推理，可以發展出不同的數學新分支，豐富數學理論。