基于LS-SVM 的月降水量預測研究

李海波 廈門大學嘉庚學院

引言

降水是生態環境對氣候變化響應的一個重要變量，未來一定時期降水量的預測，對于區域水資源規劃和分配至關重要，關系國計民生。然而，降水量受各種因素的影響，且影響程度和方式很難確定。對于降水量的預測目前主要有兩種方法：一種是采用統計模型進行預測；一種是結合回歸分析進行預測。這兩種方法在國內外運用較為廣泛，也取得了相應的研究成果。

混沌最開始是研究天氣預報的“蝴蝶效應”，從時間序列來研究混沌，開始于Packard 等人提出的重構相空間理論。目前，已經有很多種方法被應用于混沌時間序列預測研究中，如基于神經網絡預測和最小二乘支持向量機預測方法。

由于氣候具有一定的持續性，月降水量與過去幾年的數據相關性更大，在短期內系統的動力學特性具有一定的混沌特性。本文采用最小二乘支持向量機(LS-SVM)預測方法，用前t 年數據作為樣本，以預測后一年數據。本文使用的資料是國家氣候中心整編的1951 ～1995 年中國160 站月降水量資料。

1 原理及實現方法

1.1 相空間重構

要對混沌時間序列預測，首先要進行相空間重 構。 對 混 沌 時 間 序 列{y(i)}， 進 行 重 構 相 空 間，其中yi為重構矢量，τ為時間延遲，m 為嵌入維，T 表示轉置。

1.2 最小二乘支持向量機(LS-SVM)

支持向量機(Support Vector Machine,SVM)[10] 是Vapnik等人首先提出的。支持向量機是建立在統計學習理論（VC 維理論）和結構風險最小化原則基礎上的，在有限的樣本下，能夠獲得最好的泛化能力。

最小二乘支持向量機 (Least Squares Support Vector Machine,LS-SVM) 和SVM 的 區 別 就 在 于，LS-SVM 把SVM 中的不等式約束變為等式約束，SVM 中的問題是QP 問題，而在LSSVM 中則簡化為解一個線性方程組。與人工神經網絡相比，它能克服訓練時間長、訓練結果存在隨機性以及過學習的不足。

LS-SVM 回 歸 模 型：y(X)= ∑αiK(X,Xi)+b〗，其 中K(X,Xi)稱為核函數，b 為偏置量。通過求解上述線性方程組，得到優化變量α 和b 的值。

2 模型應用

以某地區為研究區域，數據選取該地區1980—1992 年每月的降水量。首先計算最大Lyapunov指數為0.21，說明該時間序列是混沌的，并可預測。用Liangyue Cao 算法計算嵌入維得m=2，用C-C 算法[13]計算時間延遲得τ=4。LS-SVM 模型參數設置為：[x(k),x(k-τ)]作為輸入樣本，x(k+1)作為目標樣本，RBF_kernel 作為徑向基核函數，回歸參數設置為gam=100，核函數設置為sig2=1。1980-1989 年共10 年數據作為訓練數據，1990 年數據作為測試數據，得到表1 和圖1；1981-1990 年共10 年數據作為訓練數據，1991 年數據作為測試數據，得到表2 和圖2；1982-1991 年共10 年數據作為訓練數據，1992年數據作為測試數據，得到表3 和圖3。

表1 1990 年月預測降水量和實測降水量對比分析結果

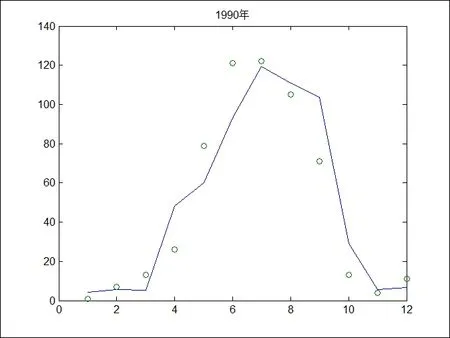
圖1 1990 年預測月降水量和實測降水量對比圖（實線為預測值，圈號為實測值）

表2 1991 年月預測降水量和實測降水量對比分析結果

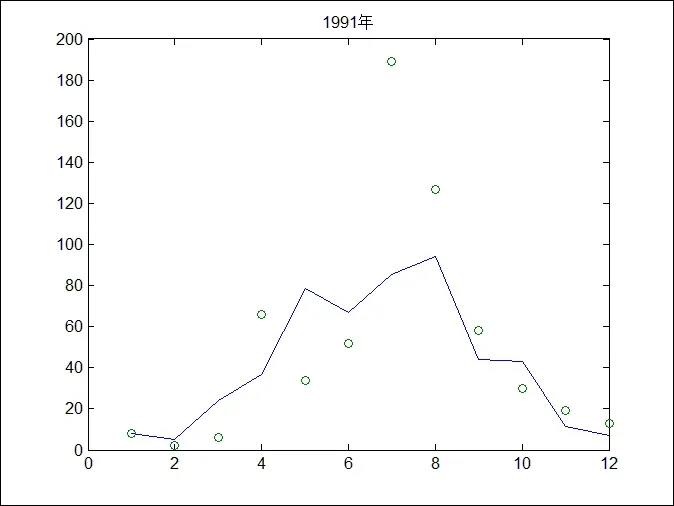
圖2 1991年預測月降水量和實測降水量對比圖（實線為預測值，圈號為實測值）

表3 1992 年月預測降水量和實測降水量對比分析結果

圖3 1992 年預測月降水量和實測降水量對比圖（實線為預測值，圈號為實測值）

表1、表2 和表3 為研究區域LS_SVM 模型預測的月降水量和實際降水量之間的對比，從三個表中可以看出，LS_SVM 模型預測的月降水量和實測的月降水量之間大部分數據的相對誤差不大，但是降水量少的月份相對誤差很大，這是因為當月降水量太小，造成相對誤差很大。圖1、圖2 和圖3 為LS_SVM 模型預測的1990 年、1991年和1992 年的月降水量和實測的月降水量對比圖。可以看出，LS_SVM 模型對這三年預測的月降水量和實測的月降水量均具有較好的趨勢吻合度。

3 結論

由于月平均降水量的變化具有混沌的特性，建立了基于LSSVM 的時間序列模型預測月平均降水量。得出如下結論：該預測模型可以對降水量的量值和趨勢同時進行預測，在該地區月降水量預測值和實測值具有較高趨勢吻合度。該模型僅用歷史降水量來預測未來降水量，然而降水量受諸多因素的影響，本模型沒有添加這些因素，因此在預測精度上還有欠缺，下一步需要細化各種因素，使之進入預測模型，使模型更加完善，以期更加符合實際情況。