改進LK光流法在復雜環境中對移動小球目標追蹤①

劉夏軒德,沈丹峰,張旭祥,張國英

(西安工程大學 機電工程學院,西安 710048)

引言

板球系統是一個欠約束、強耦合的控制系統,通過對球的位置的檢測、跟蹤、定位,從而控制小球運動.無論是對小球位置的識別還是控制小球運動都可以應用到實際的工程中.通過對小球識別方式的不同主要可以分為基于視覺、基于光電晶體管以及基于觸摸屏[1]的板球系統.近今年來計算機視覺飛速發展,從早先的車牌號識別到如今的刷臉識別、行人闖紅燈提示,計算機視覺技術被應用到越來越多的地方,手機、旅游景點、以及安檢等場所.基于視覺的板球系統研究有機的將計算機視覺與控制理論結合起來,因此對移動小球的研究具有重要的應用價值.小球的追蹤主要采用攝像頭采集圖像,通過圖像識別來追蹤小球.特征提取在機器視覺當中占據重要位置,大量應用在目標檢測、目標識別等領域[2].目前使用較多的移動目標跟蹤方法有:基于區域匹配相關的跟蹤方法；基于對比度的跟蹤方法；基于變形模板的跟蹤方法以及基于光流的追蹤方法[3]等.直方圖投影是基于區域匹配相關的跟蹤方法[4],該方法利用概率進行模板匹配,首先獲得匹配模板的圖像直方圖,然后對需要追蹤的圖像進行歸一化處理,得到若干個小的與模板尺寸相等的圖像并且得到這些直方圖,與模板直方圖進行比較選取最為相似的確定為被最終目標.基于峰值的對比度跟蹤方法[5]是選取圖片中最亮的點(既圖像函數的峰值點)以及最暗的點(圖像函數經倒向相后的峰值點)分別為白目標、黑目標,然后將其作為參考點進行追蹤的方法,也稱峰值追蹤.變形模板的跟蹤方法[6]與模板匹配方法相似,但不同的是模板為含有紋理的面板,每條紋理通過x方向及y方向變形逐漸與圖像中的真實目標相適應,從而檢索出復雜背景下的目標.

本文主要研究內容是基于LK 光流法的改進,在假設亮度不變的情況下[7],通過亮度相同這個條件在視頻流中找到與前一幀亮度相同的特征點,在追蹤的過程中會得到運動場景中特征點的運動方向和運動速度等重要信息,而特征點的運動方向和運動速度則構成了光流法的核心光流場.

近幾年的研究中光流的計算方法主要有以下幾種方法:微分法,匹配法、基于能量的方法、基于相位的方法、神經動力學方法等[8,9].移動目標追蹤實時性要求高,然而稠密光流計算需要對空間所有的像素點進行微分計算,計算量異常的大,屬于計算密集型的算法,難以確保其實時性.在此基礎上稀疏光流應運而生,只需求取其特征點,再對其特征點進行追蹤,因此大幅度減少了計算量,實時性得到的有效的提高,典型代表為LK 法[10].

對于板球系統,傳統的LK 光流法追蹤小球的運動需提取小球的特征,但顏色單一小球內部灰度梯度變化不大,特征點通常為小球的邊緣位置,難以自動捕捉到圓心,造成圓心位置計算出現誤差.因此本文對傳統的LK 光流法進行改造,應用霍夫變換[11]提取圓心位置,對確定的圓心計算灰度梯度使用LK 光流法進行追蹤,提高了LK 光流法追蹤小球圓心的準確性.同時在對圓的識別中也可以采用傳統的直方圖變換來進行,對這兩種方法在板球系統中對于小球的識別性能作出比較,確定改進LK 光流法更為適用板球系統中移動小球的捕捉.

1 基于Hough 變換的改進光流法

本文以反向直方圖投影法、LK 光流法作為該方法的對照方法.反向直方圖投影法首先計算需要追蹤目標模板的直方圖,其次將記錄的圖像進行歸一化,分割為無數個小圖像并計算每一個小圖像的直方圖,最終比對模板直方圖與小圖像的直方圖,其中與模板直方圖最為相似的直方圖所屬是小圖像即為需要追蹤的目標.

LK 光流法是利用人眼觀察運動物體時,物體的影像會在視網膜上形成一系列連續變化的圖像,這一系列連續變化的圖像平面信息不斷“流過”視網膜,好像一種光的“流”[12].光流法研究的是像素運動的瞬時速度,其原理是利用圖像序列中像素在時間域上的變化以及相鄰幀之間的相關性來找到上一幀跟當前幀之間存在的對應關系,從而計算出相鄰幀之間物體的運動信息的一種方法.

盡管采用傳統的LK 光流法可以對小球進行追蹤且相對穩定,但是該方法通常只能捕捉灰度梯度大的地方作為角點,通常為物體輪廓邊緣,很難捕捉出圓心.同時LK 法屬于在線追蹤,每一張圖片的追蹤角點信息都是參照上一幀圖片,如果上一幀角點信息丟失,則會選取新的角點,所以無法保證參考角點位置和數量的固定.如圖1所示,(a)、(b)兩圖為小球的同一運動過程,小球先經過圖(a)位置1 隨后經過圖(b)位置2,由于LK 法屬于在線追蹤,圖(a)和圖(b)的角點位置不 能完全重合,數量也不對等.

圖1 LK 光流法追蹤小球角點位置和數量

因此本文對傳統LK 光流進行改進,引入霍夫圓變換來方便確定小球中心,使角點自動確定為圓心,再進行光流法進行追蹤.為保證追蹤效果,每間隔一段時間會再次調用霍夫變換對圓心進行矯正,提升LK 光流法在復雜背景下對小球圓心捕捉的準確性.

1.1 霍夫圓變換原理

霍夫圓變換的基本原理可以概括為:圖片中的每一個非零像素點都有可能是一個潛在的圓上的一點.通過投票,生成累積數量或是累積權重來確定圓.這種方法能夠準確的提取圓心,如圖2所示為霍夫圓變換對小球的識別.

圖2 霍夫圓變換對小球的識別

1.2 基于LK 光流法的改進

通過霍夫圓變換可以確定小球的圓心位置從而得到圓心坐標(x,y),通過求取該點的灰度梯度值Ex=,使用光流法對該點進行追蹤完成對小球的追蹤,其流程步驟如圖3所示.

1.2.1 視頻預處理

視頻預處理主要分為以下幾個步驟.1.提取視頻；2.高斯濾波；3.增強邊緣.

霍夫圓變換的邊緣檢測算法利用的是圖像強度的一階和二階導數,不過導數對噪聲很敏感,通常情況下圖片或多或少都會存在一定的噪點,因此必須采用濾波器來改善圖片的噪聲質量,本文采用的是高斯濾波.同時增強邊緣的目的是為了更加有效的提取輪廓線,因此需要對圖像進行灰度化處理其次修改對比度增強邊緣.之后對視頻的預處理結束之后進行小球的追蹤.

1.2.2 修改dp 分辨率

dp 是圓心的累加器圖像的分辨率與輸入圖像之比的倒數,該參數與小球捕捉準確性關系近似為二次函數,通過調整該參數確定最佳數值提高小球捕捉準確性.

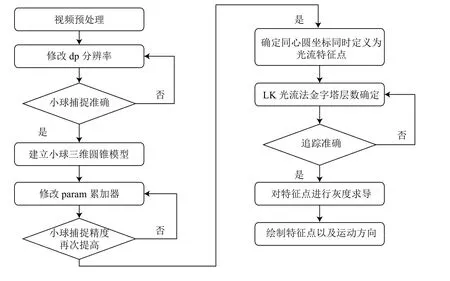
圖3 改進LK 光流法流程圖

1.2.3 建立小球三維圓錐模型

在笛卡爾坐標系中圓的方程表示為:

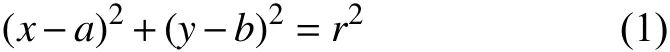
其中,(a,b)是圓心,r是半徑,用極坐標方程表述為:

令笛卡爾坐標系是圖像空間,構造abr 三維坐標系作為參數空間,在參數空間中的一個點對應圖像空間的一個圓,于是笛卡爾坐標系中經過某一點的所有圓映射到abr 坐標系中就是一條三維圓錐.經過笛卡爾坐標系中所有的非零像素點的所有圓就構成了abr 坐標系中很多條三維圓錐.因為笛卡爾坐標系中同一個圓上的所有點的圓方程是一樣的,它們映射到abr 坐標系中的的點也就是是同一個點,在abr 坐標系中該點就應該有圓的總像素N0個曲線相交.只要判斷abr 中每一點的相交(累積)數量,大于一定閾值的點就認為是小球,接下來獲得確切的半徑范圍,以及圓心坐標(x,y),將小球模型得到的圓心坐標(x,y)確立為特征點.

1.2.4 修改param 累加器

param2 表示檢測階段圓心累加器的閾值,同樣該參數與小球捕捉準確性關系近似為二次函數,通過調整該參數確定最佳數值再次提高小球捕捉準確性.

1.2.5 LK 光流法金字塔層數確定

在LK 法中金字塔金字塔主要解決相鄰幀之間特征點位移變化較大,光流法追蹤不準確的問題.通過提高金字塔層數來提高LK 法追蹤精度.

1.2.6 對特征點進行灰度求導

對于該特征點(x,y) 在時刻t的灰度為定義為E=[Ex,Ey,Et]T,該點的水平分量為u(x,y)和垂直移動分量v(x,y).于是

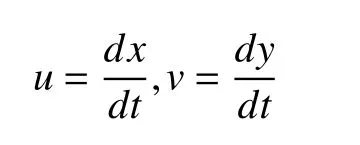
經過t+Δt,假設運動后該點的灰度則為Et=[Ex+Δx,Ey+Δy,Et+Δt]T,當Δt→0時,可以認為他們的灰度不變,于是

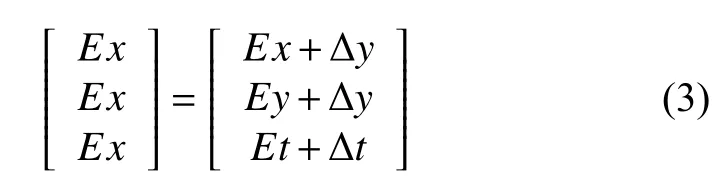
對Et進行泰勒展開同時略去二階無窮小,有:

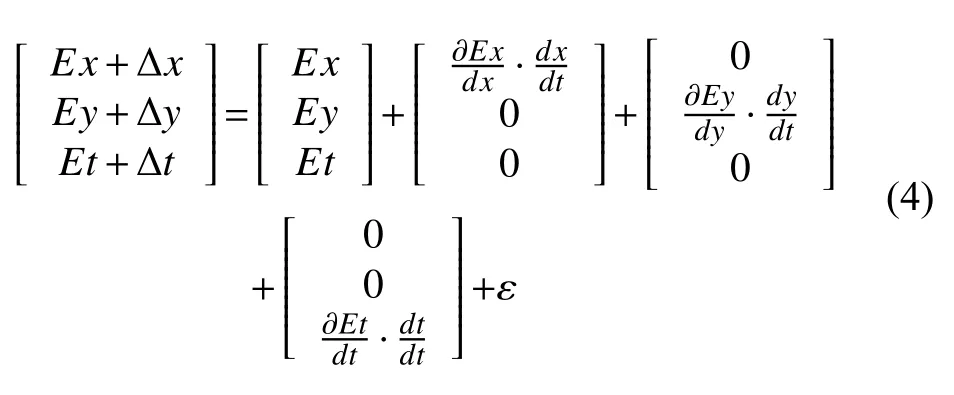
帶入式(3)化簡得

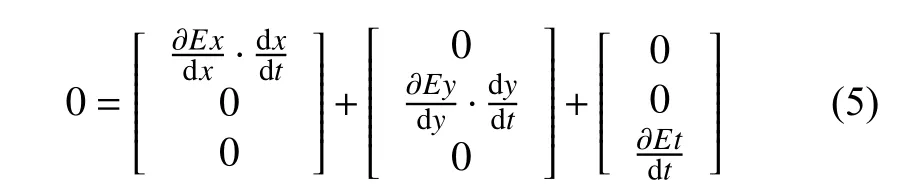
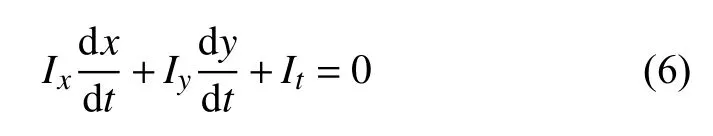
對下一幀圖片的像素點坐標(x,y)的鄰域范圍內進行灰度求導得出一系列新的水平分量和垂直分量,利用式(6)確定亮度不變點為追蹤點,最后,繪制特征點以及運動方向.

2 實驗

本文的實驗均為同一臺電腦,基本配置如下:CPU:i5-7300HQ,內存:8 GB DDR4 2400 MHZ,攝像頭:720 P.

為了后續實驗的方便進行,利用灰度直方圖對以下三幅背景圖片進行定義.

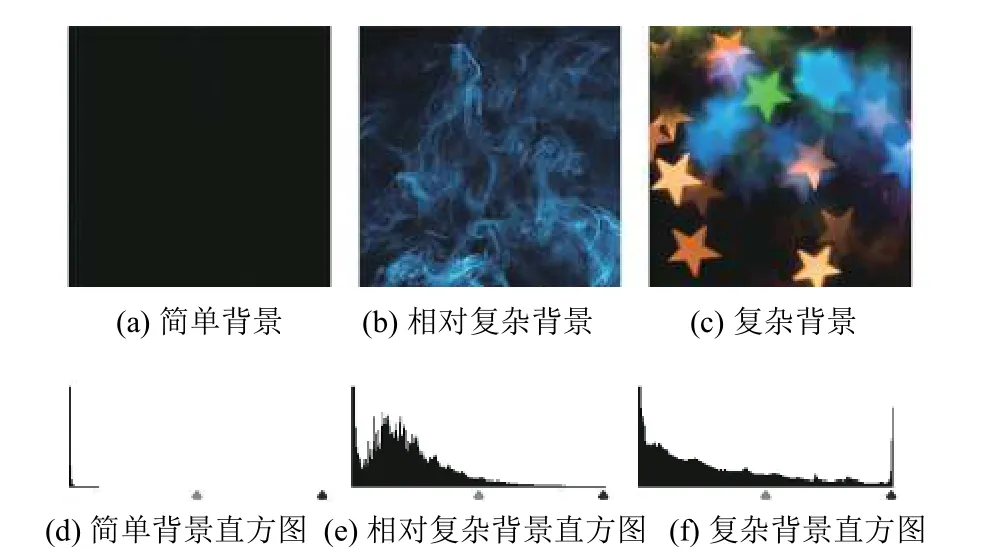
圖4 背景圖片及其直方圖

由圖4中(a) 的灰度直方圖分布十分集中,標準差0.865132 和灰度均值0.163566 最低,定義為簡單背景.圖4(b)的灰度直方圖分布相對圖4(c)的灰度直方圖分布相對來說較為松散,標準差32.6324 和灰度均值53.3734 處于圖4(a)、(c)中間,定義為相對復雜背景.圖4(c)的灰度直方圖分布相對圖4(b)的灰度直方圖分布更為松散,標準差6 0.0 3 0 7 和灰度均值61.7127 最高,定義為復雜背景.

本實驗主要分為以下兩個部分,第一部分關于改進光流法參數的選定以及準確率的影響,第二部分在三種不同背景環境下比較反向直方圖投影法、LK 法以及改進LK 對小球追蹤速度.

2.1 相關參數的選擇

2.1.1 dp 參數

dp 是圓心的累加器圖像的分辨率與輸入圖像之比的倒數,此參數允許創建比輸入圖像分辨率低的累加器.dp 累加器與輸入圖像分辨率成反比關系dp=1,累加器和輸入圖像分辨率相等,當dp=2 累加器分辨率僅為輸入圖像的一半高度和寬度.在板球系統中測試區間為[1,4]的dp 值對小球捕捉的影響,測試結果如圖5所示.

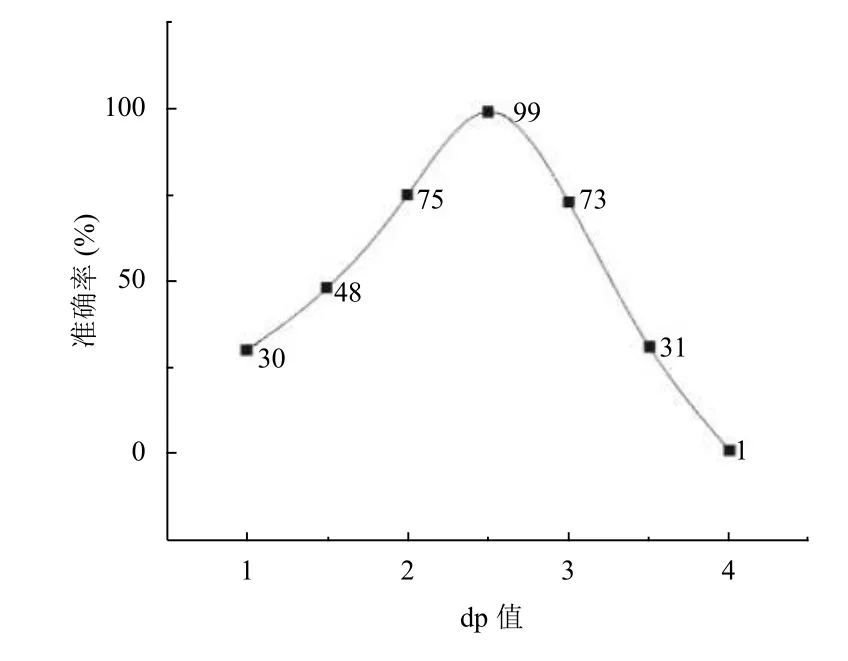
圖5 dp 值與準確率關系

當dp 值處于2.5 時準確率最高,當dp∈[1,2.5)會出現捕捉不上圓的情況,dp 值越小越難捕捉如圖6(a),當dp∈(2.5,4]會捕捉不存在的圓,dp 值越大捕捉的不存在圓越多如圖6(b).

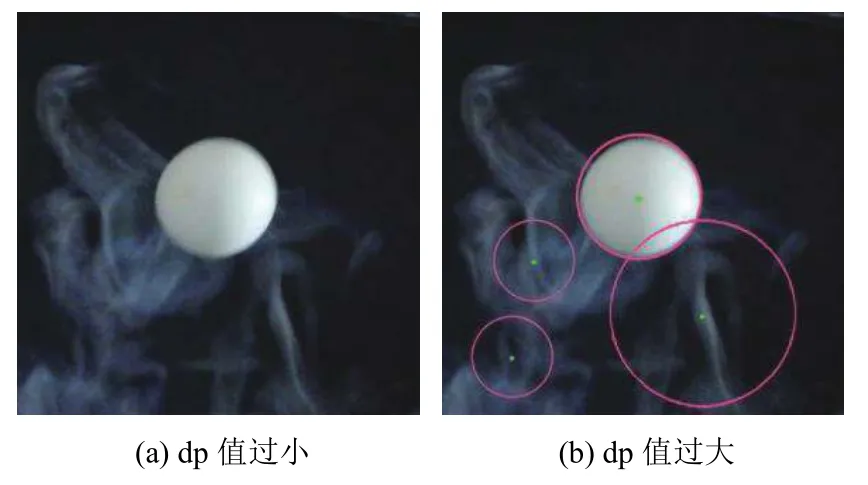
圖6 dp 值引起的誤差

2.1.2 param2 參數

param2 表示檢測階段圓心累加器的閾值.閾值越小,則檢測到更多根本不存在的圓,反之越大,通過檢測的圓更為接近標準的圓.在板球系統中測試區間為[80,200]的param2 值對小球捕捉的影響,測試結果如圖7所示.

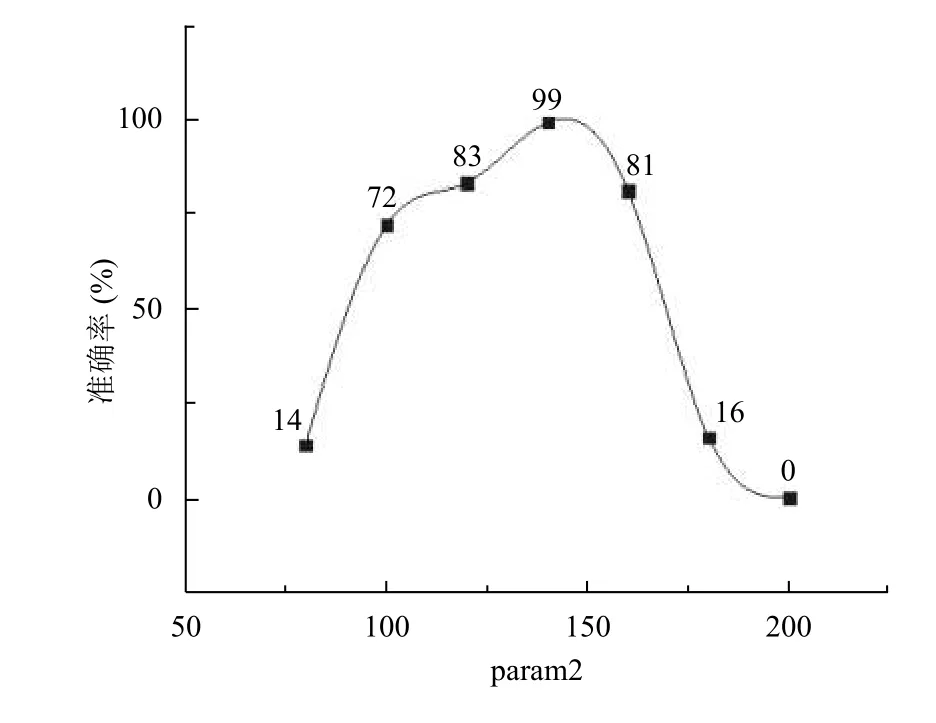
圖7 param2 值與準確率關系

當param2 值處于param2∈[140,150]時準確率最高,當param2∈[80,140)會出現捕捉不存在圓的情況如圖8(a),當param2∈(150,200]會捕捉不上的圓如圖8(b).

圖8 param2 值引起的誤差

2.1.3 maxLevel 參數

在LK 法中金字塔層數是影響著圖像光流變化準確性的一個重要因素,金字塔主要解決相鄰幀之間變化較大,光流法追蹤不準確的問題.假設底層L0為800×800 分辨率的圖像,若兩幀之間像素點位移為50×50,使用金字塔迭代至第Ln層,圖像尺寸和像素點位移均縮小2L,使用迭代后的圖像進行光流計算,并將計算得到的光流值逐層帶入直至底層L0.

本次取金字塔層數[1,6],觀察金字塔層數對于小球捕捉的影響,如圖9所示.

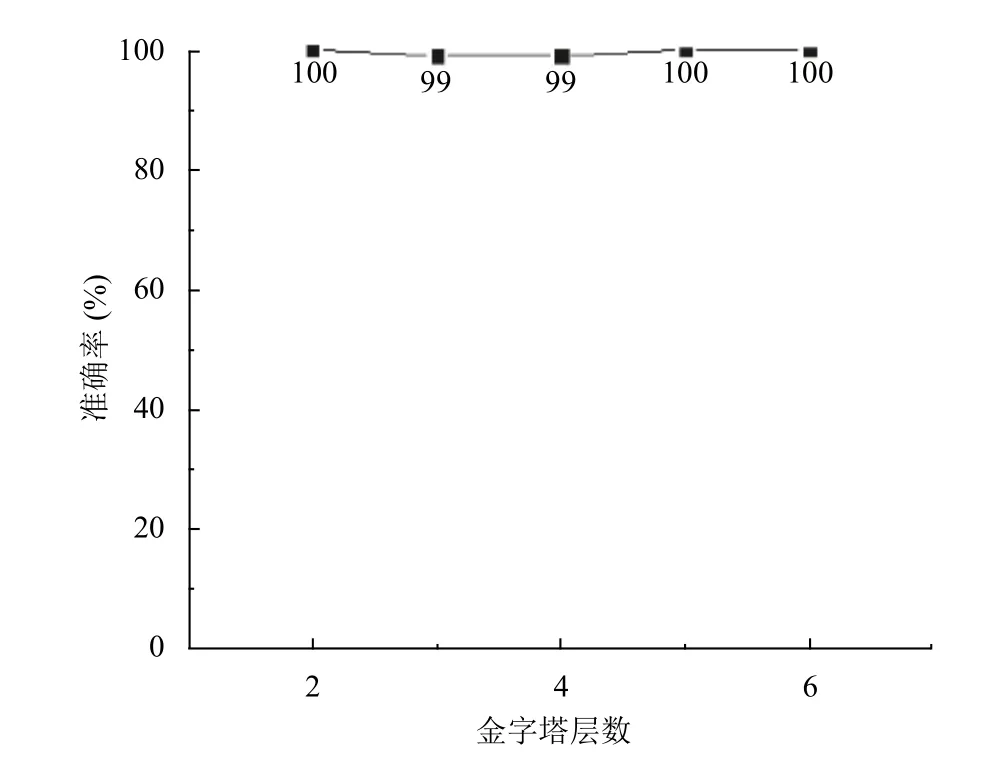
圖9 金字塔層數與準確率關系

當金字塔層數[1,6]時,準確率非常的高,且隨著金字塔層數增加也沒有明顯的變化,因此選擇1 層金字塔作為迭代層數.

2.2 不同背景下的小球捕捉的速度

分別使用反向直方圖投影法、LK 光流法以及改進LK 光流法在簡單背景相對復雜背景以及復雜背景三種情況下對小球進行捕捉跟蹤如圖10所示(時間為1 min).

圖10 上述三種方法在不同的背景下追蹤小球

上述三種方法分別在簡單背景、相對復雜背景及復雜背景下對小球目標追蹤進行,追蹤小球的每一循環程序平均運行時間數如表1.

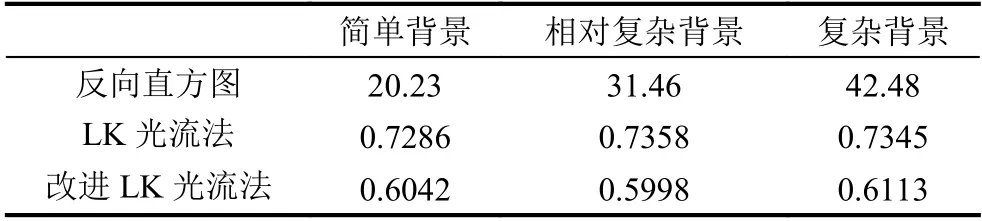
表1 運行時間(ms)

3 結果與討論

所有光學鏡頭都存在幾何失真,幾何失真是由于鏡頭平面不同區域對圖像放大率不同而形成的變形現象,該現象在畫面兩邊最為明顯.因而導致了小球成像并非一個完整的圓,因此不能要求d p 值最低和param2 值最高.

霍夫圓變換的邊緣檢測算法利用的是圖像強度的一階和二階導數,當圖像噪點過大會影響邊緣檢測的準確值,應當選取成像噪點小的攝像頭.

LK 法中增加金字塔迭代層數對于小球捕捉準確率幾乎沒有影響,主要因為在板球系統中小球的運動速度不高,視頻尺寸不大,圖像沒有出現不連貫的情況,發揮不出金字塔迭代的優勢.

通過表1可以看出反向直方圖追蹤小球在三種背景下追蹤小球十分穩定,同時小球目標追蹤方框流暢沒有出現追蹤卡頓或者目標丟失情況.但是隨著背景復雜程度的提高,運行速度逐漸減慢.總體而言反向直方圖法表現良好,但是從程序運行速度上看,該方法運行速度還是不夠理想.

可以發現無論是應對簡單背景還是復雜背景,光流法捕捉目標十分穩定,從運行速度來看LK 法在這三種情況下分別提高了27.77、42.76、57.53 倍,運行速度有一個很大的提高.同時面對三種不同情況的背景該方法的運行速度相差很小.

修改后的光流法與反向直方圖法相比,運行速度分別提高了33.48、42.76、69.49 倍.雖然基于LK 的改進方法運行速度較傳統的LK 法沒有明顯的提高,但是改良了傳統LK 法無法直接捕捉小球圓心這一弊端,可以直接定位圓心位置坐標方便后續板球系統的控制.提高了后續控制的精度.究其原因是因為該反向直方圖投影法匹配時采用的是平方差匹配法,其原理公式如下:

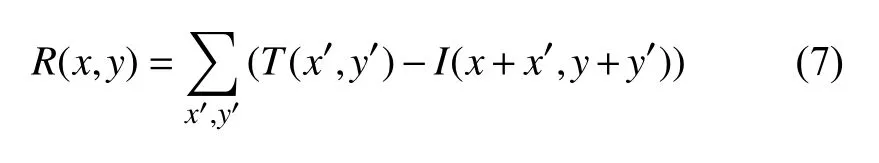
若匹配的平方差為0 則為最優,反之數值越大則越差.假設(x,y)為模板像素矩陣,(x’,y’)為圖像歸一化后的像素矩陣,由公式(7)可以得到為了得到與模板相匹配的目標需要用模板對歸一化后的每一個像素矩陣進行匹配,計算平方差.相當于對圖像的每一個像素都進行了運算,運算量龐大,所以導致了反向直方圖法與兩種光流算法相比運行速度最慢.

LK 光流法主要是通過角點進行追蹤,角點主要提取的是灰度梯度較大的地方,而這些地方通常存在于物體的邊界.同時角點的數量可通過精度的設置來改變,只需要對角點及其鄰域的像素進行計算,與反向直方圖相比像素點計算數量大幅度減少,所以速度提升非常快.

改進LK 光流法只需計算一個像素點及其鄰域像素,與傳統LK 法相比像素點的計算數量又一次降低,但是由于減少的像素點數量跨度很小,速度與LK 法相比提升不是十分明顯.

4 結束語

本文采用反向直方圖投影法、LK 法以及改進后的LK 法在三種不同的背景下對小球進行追蹤,改進后的LK 光流法更為適合板球系統中對小球的追蹤:

(1) 使用LK 法追蹤小球相較反向直方圖投影法大幅度提高了運行速度,但無法捕捉球心坐標.

(2) 通過將霍夫圓變換引入LK 法得到改進的光流法,對小球進行追蹤,小球球心點不會丟失,追蹤準確.