考慮擁堵路況下碳排放的選址-配送集成優化問題
任 慧, 王東宇
(1.西安理工大學 經濟與管理學院,陜西 西安 710054; 2.西安理工大學 機械與精密儀器工程學院,陜西 西安 710048)
0 引言
隨著全球人口和經濟規模的不斷增長,環境問題不斷凸顯。在可持續發展理念下,人們意識到只有低碳經濟模式才能實現經濟社會發展與生態環境保護的雙贏。在國際上,英國早在2007年就開始鼓勵企業推廣碳標簽的使用,目前碳標簽已普及到世界各國。據不完全統計,全球21%的碳排放來自運輸過程[1],因此,在實施了產品碳標簽以后,許多國際知名連鎖零售企業都不同程度的調整了整個供應鏈中各節點的選址及產品的配送策略。同時,Sundarakani等[2]研究供應鏈網絡設計過程中的碳足跡,證實了供應鏈中跨階段長距離運輸過程中的碳排放會對環境造成巨大威脅。供應鏈運輸過程中,影響碳排放的因素有運輸距離、路況、車輛載重等,而設施選址對運輸距離和路徑選擇產生較大影響。因此,研究考慮碳排放的選址-配送集成問題(Collaboration of Location-Distribution Problem, CLDP)具有實際意義。
Corbett等[3,4]最先開始探討如何將環境問題納入到優化供應鏈運作中,尤其是引入到運輸過程中。隨后,學者們大致從三個方面將碳排放問題融合到供應鏈運輸過程中:(1)將碳排放轉化為經濟成本的一部分。李劍等[5]將碳稅納入到運輸成本中研究復合碳政策對供應鏈運輸過程的影響機理。(2)以碳排放作為約束條件。Diabat等[6]以碳配額作為供應鏈系統成本的約束條件來研究設施選址問題。(3)以碳排放量最小為目標之一,構建多目標決策模型,權衡碳排放量和系統成本、配送時間等。Wygonik等[7]研究了城市配送系統中二氧化碳排放量、成本和服務質量之間的權衡;Demir等[8]研究了同時考慮燃料消耗量和配送時間的配送污染問題;Wang等[9]根據減排的強度確定設施選址和運輸模式,設計了考慮碳排放量和成本的供應鏈網絡。由于多目標決策方法可以兼顧問題的客觀性和決策者的偏好性,本文也將采用該方法研究考慮碳排放的選址-配送集成問題。
此外,也有一些文獻研究運輸過程中碳排放量的影響因素。Simt等[10]指出車輛行駛的距離對碳排放有很大的影響。同時Carslaw[11]和Lefebvre[12]調查發現在運輸過程中車輛速度是決定碳排放的一個重要決定因素,尤其在高速公路上,某一限制速度下行駛的距離決定碳排放的降低程度。因此,一般認為影響運輸過程中,碳排放量主要受車輛行駛距離和速度的影響。在行駛距離固定的情況下,路況是決定車速的主要原因,其中包括道路限速和擁堵情況。Zhang等[13]研究了道路擁堵情況下機動車的碳排放量,指出交通擁堵程度影響碳排放量。一些學者認為擁堵情況下,車輛加速和減速的頻繁交替會明顯增加碳排放量[14~16]。由于限速不可控,擁堵情況被認為是影響交通碳排放量的一個主要因素。
目前考慮擁堵路況下碳排放的文獻中主要分析不同擁堵程度對碳排放量的影響。例如:Figliozzi[17]以波特蘭城市配送系統為例,主要分析不同擁堵水平和硬時間窗下二氧化碳排放量。Grote等[18]提出利用不同類型的道路交通數據和排放模型估計不同擁堵尺度上的交通排放量。戢守峰等[1]通過設置4級擁堵狀況,研究考慮擁堵和限速路況下碳排放的三級供應鏈網絡設計。然而,實際中擁堵水平的劃分標準并不統一,且按等級劃分擁堵水平通常是用于綜合反映道路網通暢或擁堵的概念性指標,這些定性的指標很難對碳排放量進行定量刻畫。因此,需要對擁堵程度進行定量化研究。
考慮到車輛只有處于減速、怠速、加速這三種狀態的頻繁交替中,碳排放量才會明顯增加[19,20],而保持在某一速度區間內的碳排放量變化不大[21],因此在碳排放量的研究中本文設定這兩種情況為道路擁堵和通暢。其次,對于擁堵問題的研究,多數文獻都是從時間和空間因素上估計擁堵程度[22,23],由此本文提出以不同時段下車輛行駛的預期擁堵距離,來直觀描述擁堵程度。此外,交通事故、不文明交通行為、交通流等因素會造成道路擁堵,即每條運輸路徑都存在擁堵的可能性。因此,本文以不同時段下的擁堵概率和預期擁堵距離作為研究碳排放的路況決定因素。同時,車輛載重也會影響到碳排放量[24]。基于此,本文研究考慮擁堵路況下碳排放的選址-配送集成優化問題,并以碳排放量和經濟成本最小為目標構建多目標優化模型。
1 問題描述與假設
1.1 問題描述
本文研究工廠、配送中心、零售商的三級供應鏈網絡內考慮碳排放的選址-配送集成問題,圖1給出了候選供應鏈網絡。需要選址的設施包括工廠和配送中心,分別從擁有不同能力和位置的候選工廠和配送中心中選擇。對于配送問題,既要考慮不同配送路徑產生的運輸成本,又要考慮碳排放量。每條路徑的運輸距離各不相同,相同時段內發生擁堵的概率也可能相差較大,預期擁堵距離也不盡相同。如果選擇某一時段下通過擁堵概率較大且運輸距離較長的路徑,一旦發生擁堵,車流量較大時,擁堵距離自然較長,此時碳排放量必然較多。然而,設施位置會影響配送路徑的選擇。同時,車輛載重會影響到運輸車次和碳排放量,以及單位產品單位距離的運輸成本。因此,需要合理的選擇設施位置、配送路徑和配送車輛,才能實現經濟成本和碳排放量最小。
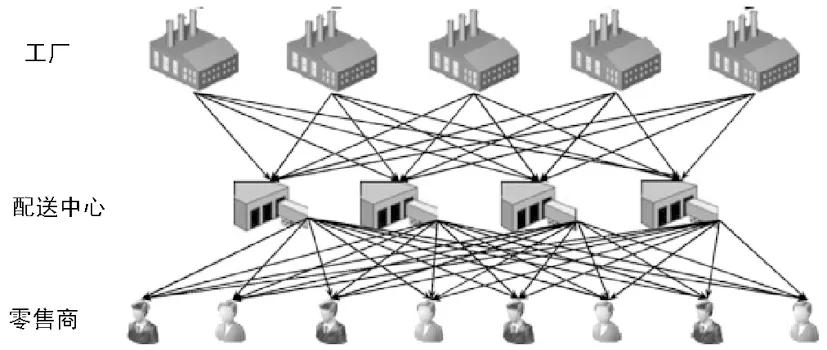
圖1 三級供應鏈網絡結構
1.2 假設條件
(1)配送中心和零售商均為單源供應,即每個配送中心由一個工廠供貨,每個零售商需求由一個配送中心提供,所有供貨均為備貨型供應。每個工廠到每個配送中心、每個配送中心到每個零售商的路徑唯一。從工廠到配送中心的路徑為高速公路;從配送中心到零售商的路徑為城市道路。
(2)工廠和配送中心具有能力約束。工廠的供貨能力不大于生產能力,配送中心的供貨能力不大于存儲能力。
(3)每條運輸路徑在不同時段下發生擁堵的概率都是隨機的,且相互獨立。
(4)通暢下的碳排放量假設。各條高速公路和各條城市道路分別設定統一的限速。根據文獻[24]對車速、載重和碳排放量的研究,得知碳排放量是關于車速的凸函數,即從發動車輛開始碳排放量先是隨著車速的增加而減少,當增加到某一速度時碳排放量達到最小值,然后隨著車速的增加,碳排放量迅速增加。對于不同載重,相同速度的碳排放量和碳排放量達到最小的速度不同。因此,假設通暢情況下的碳排放量為相應載重車輛限速內碳排放量最小值。
(5)擁堵下的碳排放量假設。以相應載重車輛在減速、怠速、加速三種狀態下的碳排放平均值設為擁堵情況的碳排放量。
(6)擁堵距離假設。在現實情況中各路段發生擁堵時,其擁堵距離為有界連續隨機變量。根據文獻[25],假設路徑擁堵距離服從對數正態分布X~ln(μ,σ2),其概率密度函數為:
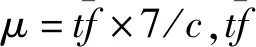
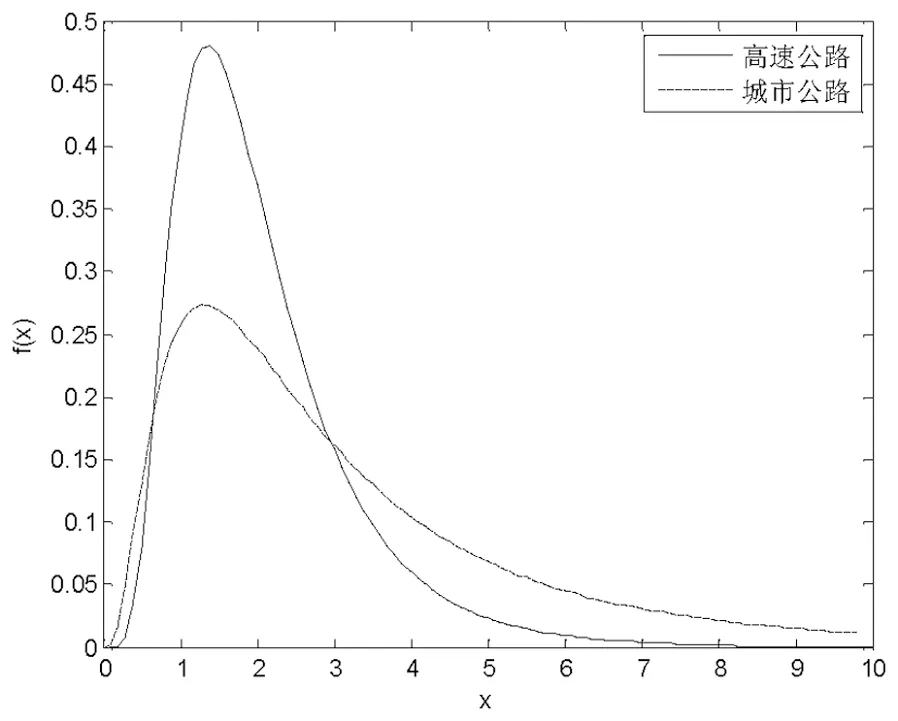
圖2 運輸路徑擁堵距離的概率分布示意圖
2 模型構建
2.1 符號說明
(1)集合。候選工廠的位置集合為M={m|m=1,2,…,1};候選配送中心的位置集合為J={j|j=1,2,…,2};零售商集合為I={i|i=1,2,…,3};高速公路24小時內路況分為T1個時段,任意時段t1=1,2,…,T1;城市道路24小時內路況分為T2個時段,任意時段t2=1,2,…,T2。
(2)容量。候選工廠m單位時間內的生產能力為km;候選配送中心j的存儲能力為wj;零售商i單位時間內的需求量為di。
(3)車輛載重。從工廠到配送中心選用載重為r1重型貨車。從配送中心到零售商選用載重為r2中型貨車。
(4)成本。綜合考慮設施的使用年限,單位時間內工廠m的構建成本為fm;單位時間內配送中心j構建成本為gj;高速公路單位產品單位距離的運輸成本為lr1,城市道路單位產品單位距離的運輸成本為lr2。
(5)碳排放量。高速公路上載重為r1的車輛在限速內通暢時單位距離的碳排放量為er1,擁堵時單位距離碳排放量為zr1。城市道路上載重為r2的車輛在限速內通暢時單位距離的碳排放量為er2,擁堵時單位距離碳排放量為zr2。
(6)路徑擁堵概率。時段t1下工廠m到配送中心j的路徑擁堵概率為qmjt1;時段t2下配送中心j到零售商i的路徑擁堵概率為qjit2。
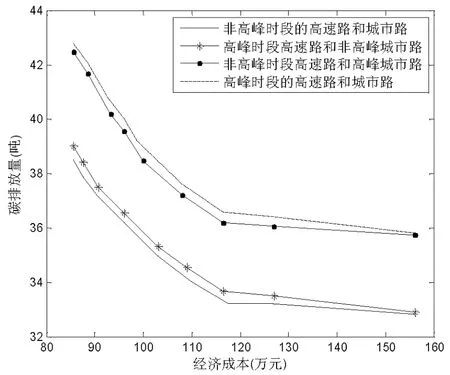
(7)距離。工廠m到配送中心j的路徑距離為cmj,時段t1下預期擁堵距離為Cmjt1,Cmjt1 其中f1(xt1)為路徑mj在時段t1下的擁堵距離的概率密度函數,f2(xt2)為路徑ji在時段t2下的擁堵距離的概率密度函數。 (8)決策變量。設施位置變量(工廠位置變量U,配送中心位置變量Z),配送變量(工廠到配送中心的配送變量X,配送中心到零售商的配送變量Y): 構建的模型包含兩個目標,一是經濟成本最小,二是不同時段下運輸過程中的碳排放量最小。 經濟成本包括選址、配送成本,具體為: (1) 單位時間內工廠選址成本,∑m∈MfmUm。 (2) 單位時間內配送中心選址成本,∑j∈JgjZj。 (3) 單位時間內配送成本包括工廠到配送中心的運輸成本和配送中心到零售商的運輸成本:lr1∑m∈M∑j∈JcmjwjXmj+lr2∑j∈J∑j∈IhjidiYji。 單位時間內不同時段下運輸過程的碳排放量為: (1) 時段t1下工廠到配送中心的碳排放量,∑m∈M∑j∈JXmj(cmj-Cmjt1)er1+Cmjt1zr1]qmjt1+cmjer1(1-qmjt1)}wj/r1。 (2) 時段t2下配送中心到零售商的碳排放量,∑j∈J∑i∈IYji{[(hji-Hjit2)er2+Hjit2zr2]qjit2+hjier2(1-qjit2)}di/r2。 綜上所述,考慮碳排放的選址-配送集成多目標(CLDCE)模型為: F1=min∑m∈MfmUm+∑j∈JgjZj+ lr1∑m∈M∑j∈JcmjwjXmj+lr2∑j∈J∑i∈IhjidiYji (1) F2=min∑m∈M∑j∈JXmj{[(cmj-Cmjt1)er1+Cmjt1zr1]qmjt1+ (2) s.t. ∑m∈MXmj=Zj,?j∈J (3) ∑j∈JYji=1,?i∈I (4) ∑i∈IdiYji≤wj,?j∈J (5) ∑j∈JwjXmj≤km,?m∈M (6) cmj>Cmjt1,hji>Hjit2,?m,j,i,,t1,t2 (7) 式(1)為經濟成本最小的目標函數,包括選址成本和配送成本;式(2)為在高速公路t1時段下和城市道路t2時段下,工廠到零售商的整個運輸過程中碳排放量最小的目標函數。式(3)保證任意選建的配送中心j只由一個工廠供貨。式(4)表示任意零售商i的需求只由一個配送中心提供。式(5)表示配送中心j的存儲能力約束。式(6)表示工廠m的生產能力約束。式(7)表示預期擁堵距離的約束。 文中利用改進的非支配排序遺傳算法(NSGA-II),對構建的CLDCE模型進行求解,獲得Pareto解集,確定合適的設施構建位置及不同時段下的配送方案,具體流程見圖3。NSGA-II求解CLDCE模型的步驟如下: Step1染色體編碼。 Step2初始化種群。根據染色體編碼,對隨機產生N的個解個體檢驗其有效性,獲得初始化種群P0。 Step3種群個體分級。將種群中的解個體進行非支配排序。 首先,對于任意解個體s,根據目標函數(1),確定目標分量f1(s)=∑m∈MfmUm+∑j∈JgjZj+lr1∑m∈M∑j∈JcmjwjXmj+lr2∑j∈J∑i∈IhjidiYji+Q(s),其中Q(s)是總的違反能力約束的罰函數,根據CLDCE模型中約束(5)~(6),Q(s)=v1(s)+v2(s),v1(s)=ε1(∑m∈Mmax{0,∑j∈JwjXmj-kmTm}),v2(s)=ε2(∑j∈Jmax{0,∑i∈IdiYij-wjZj}),v1(s)表示解個體s中工廠供應能力超過生產能力的罰函數,v2(s)表示配送中心供貨能力超過存儲能力的罰函數。對v1(s)和v2(s)設置合適的系數ε1,ε2,避免獲得的Pareto解集中含有非可行解。目標分量f2(s)即為目標函數(2)本身。 其次,根據兩個目標分量f1(s)和f2(s),找出該種群中的所有非支配個體,并賦予它們一個共享的虛擬適應度值,形成第一級非支配個體集合(Pareto解集或非支配解集)。然后對種群中的其它個體繼續按照非支配關系分級,并賦予它們一個新的虛擬適應度值,形成第二級非支配個體集合(只由Pareto解集支配的個體集合),直到所有個體都被分級。 Step4遺傳運算。 根據虛擬適應度值,對非支配排序后的種群進行復制,實施選擇運算。然后,給定交叉概率,進行交叉運算。隨后,給定突變概率,隨機選定突變基因位,當其落在染色體的第一段時,此基因發生突變的范圍為候選工廠位置集合;當其落在染色體的第二段時,此基因發生突變的范圍為候選配送中心位置集合。通過選擇、交叉、變異運算,生成子代種群Q0。 Step5實施NSGA-II主流程: 將初始種群P0與其子代種群Q0合并,形成大小為2N的種群R0。再對種群R0進行非支配排序,對產生的一系列非支配集Hi計算擁擠度。將H1,H2,…放到新的父代種群P1中,直到添加Hi時,種群的大小超出N,對Hi中的個體進行擁擠度排序,取前N-|P1|個個體,使P1的個體數為N(詳見[26])。 隨后,對種群P1實施Step3~Step5形成新的子代種群Q1,如此重復上述過程,直到設定的進化代數為止。最終,獲得終止代數的子代種群即為Pareto解集。 對于第t代種群的NSGA-II的主流程偽代碼[26]為: Rt=Pt∪Qt; H=sort(Rt); Pt+1=? 從i=1開始 計算Hi中個體的擁擠度 Pt+1=Pt+1∪Hi; i=i+1; 直到|Pt+1|+|Hi|>N sort(Hi,n); Pt+1=Pt+1∪Hi[1:(N-|Pt+1|)]; Qt+1=new(Pt+1); t=t+1 圖3 NSGA-II求解CLDCE模型的流程圖 北京是中國的政治、經濟和文化中心,由于人口量高、交通網密集導致城市霧霾逐漸加重。因此,政府著重關注北京周圍環境中的碳排放量。考慮到北京和天津這兩大重要城市的距離位置,以他們為中心在其周圍構建供應鏈網絡。在這兩個城市中共設立10個固定零售商,在其周圍城市或地區設立工廠和配送中心,其中有4處候選工廠和5處候選配送中心。綜合考慮經濟成本和碳排放量,選建工廠和配送中心、制定配送方案。 根據各零售商所處轄區的人口量,獲得年平均需求量,如表1所示。根據所處地區2016年度構建廠房和配送中心的市場平均價格設定選址固定費用[1]。以工廠和配送中心的選址規模來設定其擁有的能力。表2列出了候選工廠和候選配送中心的基本參數,并設定設施的使用年限為10年。根據文獻[24]對車速、載重與碳排放量的研究,表3給出四種載重車輛分別在高速公路和城市道路上通暢和擁堵情況下的單位距離碳排放量以及單位產品單位距離運費。 根據運輸路徑非節假日內監測的車流量數據,將24小時內的高速公路為兩個時段[27],高峰時段(早6點~晚18點),非高峰時段(晚18點~早6點);城市道路分為兩個時段[28,29],高峰時段(早7點~早10點,晚17點~晚21點),非高峰時段(早10點~晚17點,晚21點~早7點)。統計非節假日兩時段內擁堵次數[27],得出高速公路兩時段擁堵概率大致服從N(0.1,0.05)和N(0.05,0.02)的正態分布,城市道路兩時段擁堵概率大致服從N(0.5,0.1)和N(0.3,0.05)。接下來,表4和表5分別給出候選工廠到候選配送中心、候選配送中心到零售商的運輸距離和各運輸路徑高峰時段、非高峰時段的時均車流量,以及兩時段下的預期擁堵距離,其中兩時段的預期擁堵距離由各時段的時均車流量獲得。 表1 零售商需求量(單位:萬份, 每份0.5kg) 數據來自中華人民共和國國家統計局http://www.stats.gov.cn/ 表2 候選工廠和候選配送中心的基本參數 數據來自文獻[1]。 表3 不同載重車輛在擁堵和通常情況下的碳排放量以及單位運費 數據來自文獻[24]。 表4 候選工廠到候選配送中心的運輸距離(單位:公里)和2個時段的時均車流量(單位:千輛)以及預期擁堵距離(單位:公里) 注:候選工廠到候選配送中心的距離(高峰時段車流量,預期擁堵距離)(非高峰時段車流量,預期擁堵距離)數據來自文獻[27]。 表5 候選配送中心到零售商的運輸距離(單位:公里)和高峰和非高峰時段的時均車流量(單位:千輛)以及預期擁堵距離(單位:公里) 注:候選工廠到候選配送中心的距離(高峰時段車流量,預期擁堵距離)(非高峰時段車流量,預期擁堵距離)數據來自文獻[28,29]。 首先,根據表1~表5給出的算例參數,獲得CLDCE模型的輸入變量,利用設計的NSGA-II獲得考慮碳排放量的三級供應鏈網絡的設施選址和配送方案。其次,對影響碳排放量的相關因素進行CLDCE模型的靈敏度分析,其中有不同載重的運輸車輛、不同時段下運輸路徑的擁堵概率以及預期擁堵距離。 在上述給出的待構建的三級供應鏈網絡中,需要做出以下決策:(1)工廠的選址決策;(2)配送中心的選址決策;(3)哪些工廠為哪些配送中心供貨;(4)哪些配送中心為哪些零售商配送貨物。以運輸過程中,車輛在非高峰時段內通過高速公路和城市道路為路況條件,工廠到配送中心選用32噸重型貨車,配送中心到零售商選用10噸中型貨車為算例,利用設計的NSGA-II算法使用Matlab 2011b編程,獲得考慮擁堵路況下碳排放量和經濟成本的選址-配送問題的Pareto解集,如圖4所示。 圖4 非高峰運輸時段CLDCE模型的Pareto解集 從圖4可以看出,本文求得的Pareto解集均勻的分布在Utopia線的下方,一方面說明了算法及結果的有效性,另一方面,圖4提供了非高峰時段運輸下的一組Pareto解集,決策者可以根據自身的決策偏好選擇最佳的決策方案。同時,圖4描繪出了CLDCE模型中碳排放量和經濟成本之間的權衡關系,經濟成本越高,碳排放量越小,反之亦然,這說明碳排放量和經濟成本間存在一定的悖反。為了分析這一結果的原因,在Pareto前沿上選取了一些典型解,如表6所示。 表6給出了5個Pareto解,即5個方案。首先看到,隨著經濟成本的逐漸增加,碳排放量將逐漸減少;其次發現隨著經濟成本的逐漸增加,減排量出現遞減態勢,即減排量產生邊際效應。這說明當要求碳排放量低于一定程度時,單純的通過優化供應鏈運作將無法達到。進一步分析表6中工廠、配送中心的選址及配送方案,我們發現經濟成本較低的方案對應較少的設施選址,例如,方案1中只選建了一個工廠和兩個配送中心。由于產品運輸數量相對固定,只有通過減少設施構建數量來達到經濟成本最小。然而,對于碳排放量較少的方案則對應較多的設施選址,例如,方案5中選建了兩個工廠和三個配送中心。當構建的工廠和配送中心數量較多時,供應鏈網絡則相對密集,產品運輸更加便利,運輸距離相對減少,碳排放量自然降低。 為了分析不同時段下各路徑的擁堵概率、預期擁堵距離這兩個路況決定因素和車輛載重對CLDCE模型決策結果的影響。我們在選用32噸重型貨車和10噸中型貨車的基礎上,又對高峰時段經過高速公路和城市道路、非高峰時段經過高速公路和高峰時段經過城市道路、高峰時段經過高速公路和非高峰時段經過城市道路這三種情況求解CLDCE模型,圖5給出Pareto解集。隨后,我們又選用20噸貨車從工廠配送產品到配送中心,選用6噸貨車從配送中心配送產品到零售商,對上述四種路況求解CLDCE模型,圖6給出Pareto解集。 表6 載重32噸和10噸車輛非高峰時段下選址-配送集成問題的Pareto解集及決策方案 從圖5、圖6中,首先發現,當經濟成本相同時,高峰時段經過高速公路和城市道路這種情況的碳排放量最大;其次是非高峰時段經過高速公路和高峰時段經過城市道路,然后是高峰時段經過高速公路和非高峰時段經過城市道路,而非高峰時段經過高速公路和城市道路的碳排放量最小。這說明當經濟成本相同時,供應鏈網絡中跨階段待選運輸路徑的擁堵概率和預期擁堵距離整體減小,決策方案中的碳排放量就會隨之減少。 圖5 載重32噸和10噸貨車不同時段下CLDCE模型的Pareto解集 圖6 載重20噸和6噸貨車不同時段下CLDCE模型的Pareto解集 其次發現,當其他條件相同時,非高峰時段經過高速公路比高峰時段經過高速公路減少的碳排放量隨著經濟成本的增加先逐漸增加后逐漸減少,但是總體而言減少的碳排放量相對較少。這是由于非高峰時段和高峰時段高速公路的擁堵概率、預期擁堵距離相差較小。進而說明高速公路不同運輸時段對碳排放量影響較小,訂單配送不用過分苛求夜間非高峰時段。然后發現,當其他條件相同時,非高峰時段經過城市道路比高峰時段經過城市道路減少的碳排放量隨著經濟成本的增加先逐漸增加后保持不變,且減少的碳排放量相對較多。這是由于高峰時段和非高峰時段城市道路的擁堵概率、預期擁堵距離相差較大。進而說明城市道路不同運輸時段對碳排放量影響明顯,高峰時段經過城市道路會明顯增加碳排放量。因此,從配送中心到零售商的產品配送,應該避開城市道路的早晚高峰時段。 然而,進一步觀察圖5和圖6,我們發現,兩幅圖像大致分成兩段,隨著經濟成本的增加,第一段中碳排放量減少率較大,第二段中的碳排放量減少率較小。不同之處在于,圖5的第一段是經濟成本從85萬元增加到90萬元,碳排放量大致減少5噸;圖6的第一段是經濟成本從85萬元增加到116萬元,碳排放量也大致減少5噸。這說明圖5第一段的碳排放減少率要明顯大于圖6的。這是由于當經濟成本較小時,供應鏈網絡構建的相對稀疏,車輛運輸距離相對較遠,載重較大車輛的碳排放量會高于載重較小的車輛。隨著經濟成本的增加,構建的供應鏈網絡會相對密集,車輛運輸距離也會相對縮短,載重較大車輛的碳排放量會快速減少。當經濟成本在90~110萬元之間時,載重為32噸和10噸的比20噸和6噸的車輛碳排放量要小。隨后,當經濟成本從110萬元再逐漸增加時,載重20噸和6噸的比32噸和10噸的車輛碳排放量要小。 本文探討了考慮擁堵路況下碳排放的選址-配送集成優化問題。構建了碳排放量和經濟成本最小的兩目標模型,并設計NSGA-II算法獲得Pareto解集。以環境問題較重的北京和天津為中心,構建供應鏈網絡作為算例,得到以下結論: (1)偏好經濟成本較低的方案中,構建的設施(工廠、配送中心)較少,供應鏈網絡相對稀疏,運輸距離相對較長;偏好碳排放量較少的方案中,構建的設施較多,供應鏈網絡相對密集,運輸距離相對較短。 (2)待選運輸路徑的擁堵概率和預期擁堵距離整體減小,決策方案中的碳排放量也會隨之減少。 (3)根據非節假日內統計的運輸路徑高峰時段和非高峰時段擁堵概率和時均車流量,得知高速公路不同運輸時段對碳排放量影響較小;而城市道路不同運輸時段對碳排放量影響較大,高峰時段經過城市道路會明顯增加碳排放量。 (4)當構建的供應鏈網絡較稀疏時,載重較大車輛比載重較小的碳排放量多。但是隨著經濟成本的增加,運輸距離將逐漸減小,載重較大車輛的碳排放量會快速減少,甚至小于載重較小的車輛。 進一步研究方向可以探討優化供應鏈運作也無法達到碳排放量強約束下的選址-配送問題。同時還可以探討采用清潔能源汽車配送產品所投入的經濟成本與減排之間的關系。此外,還可以設計更好的方法來解決這類NP-hard問題。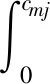
2.2 考慮碳排放的選址-配送集成優化模型
3 模型求解
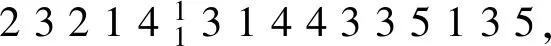
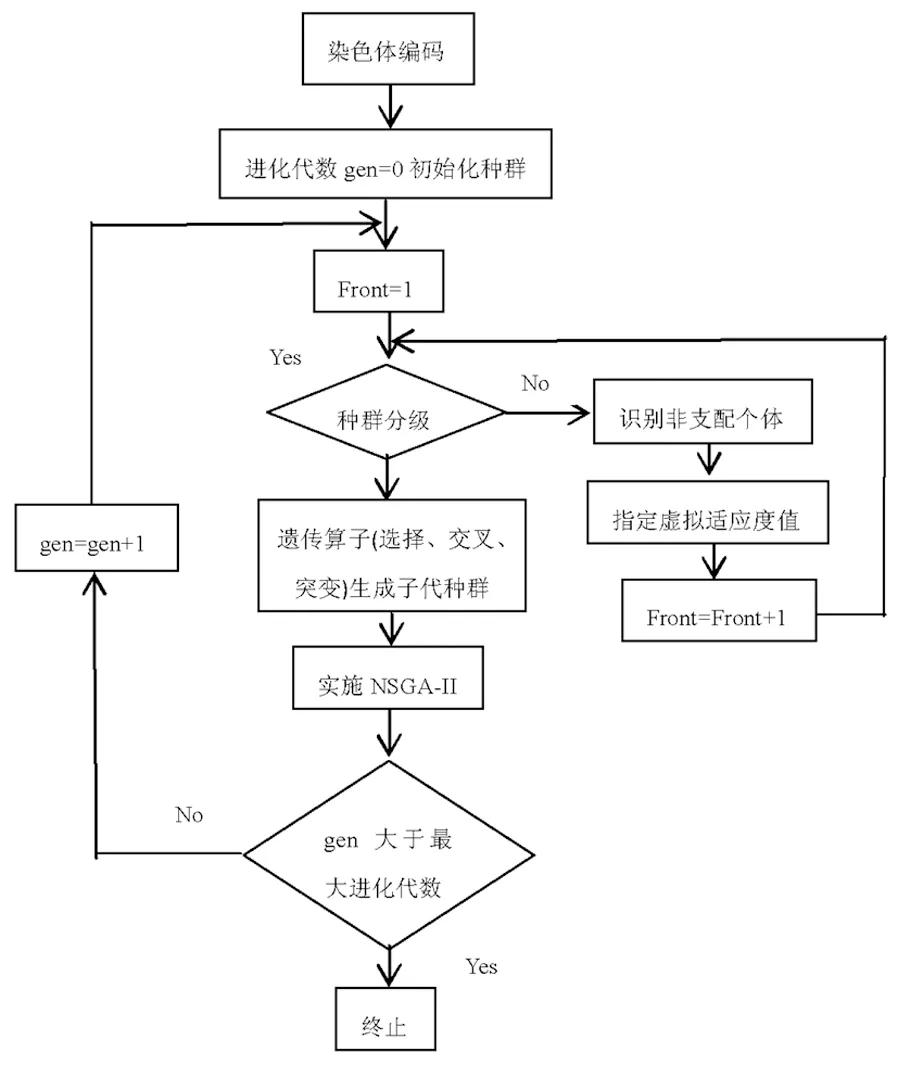
4 算例分析
4.1 算例數據來源及參數推導




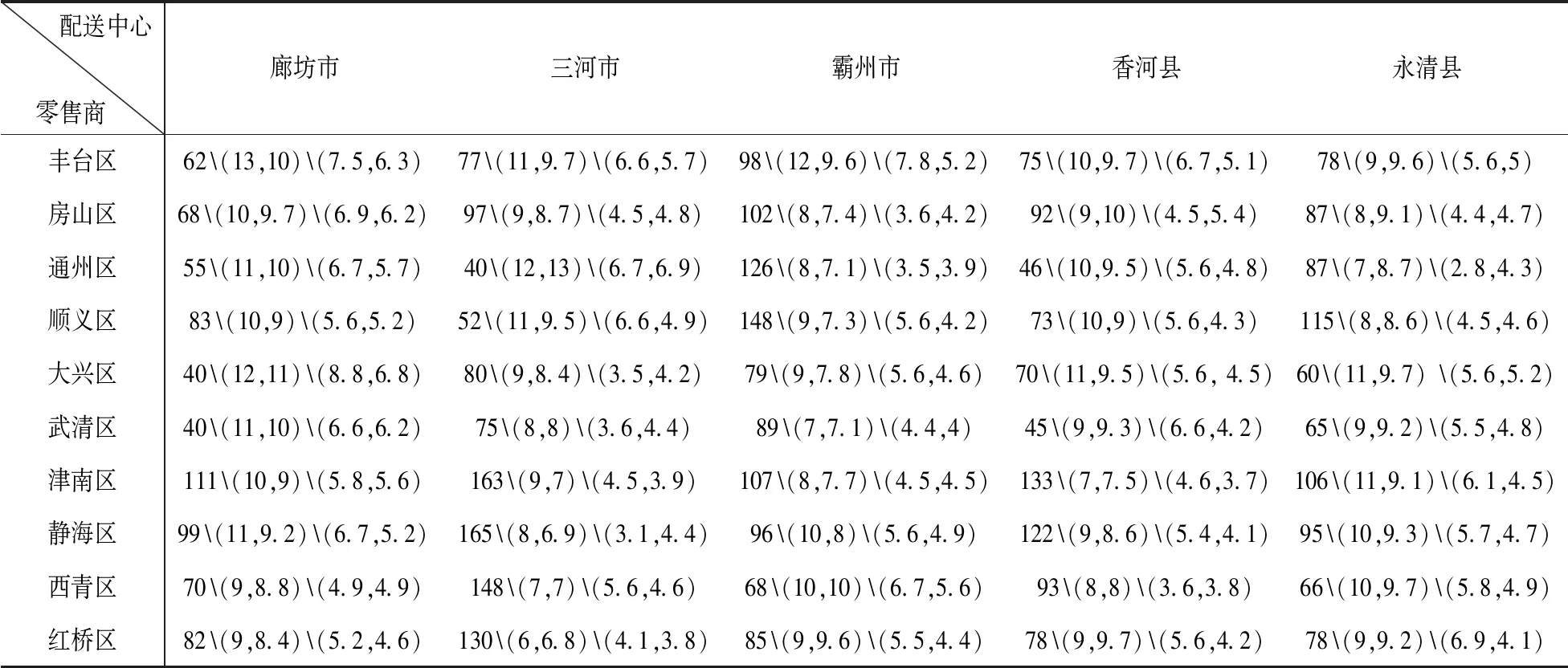
4.2 算例結果與靈敏度分析
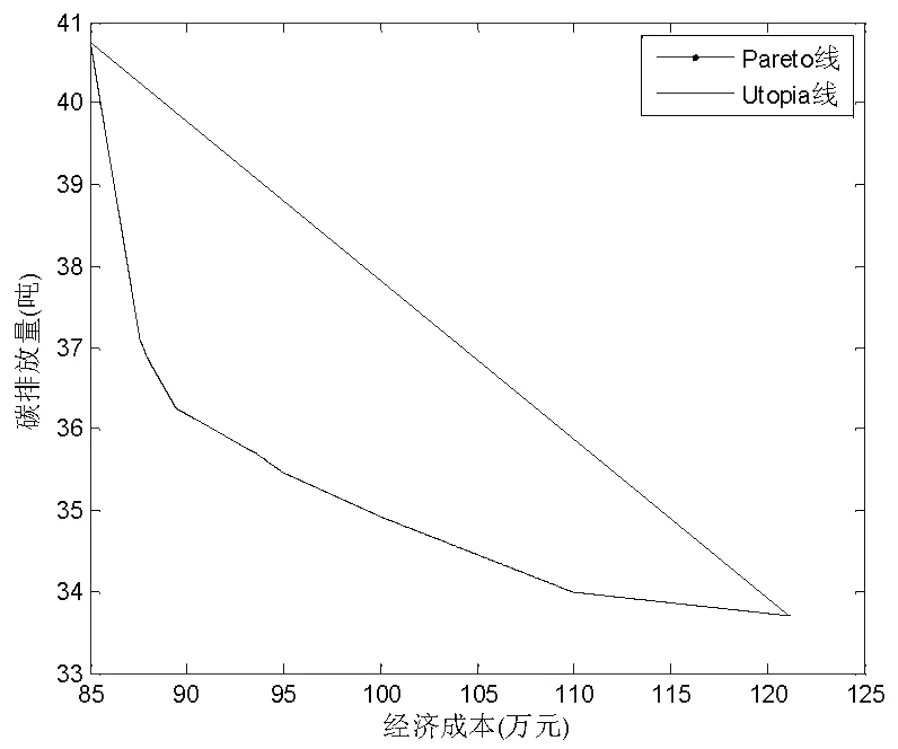


5 結論

