基于前景理論的三角猶豫模糊多屬性決策方法

王 娟， 金智新,2,3， 鄧存寶， 方 博

(1.遼寧工程技術大學 工商管理學院，遼寧 葫蘆島 125105; 2.山西焦煤集團有限責任公司，山西 太原 030024; 3.太原理工大學 安全與應急管理工程學院，山西 太原 030024; 4.遼寧工程技術大學 安全科學與工程學院，遼寧 葫蘆島 125105)

0 引言

多屬性決策是關于多個相關屬性有限方案的選擇問題，由于實際決策問題的復雜性和決策者認知的局限性，對評價信息和屬性權重難以用精確值表述。Zadeh[1]提出利用模糊集處理不確定性和模糊性評價信息，但模糊集是通過單隸屬度刻畫模糊信息，難以滿足實際決策需要。此后，國外學者對模糊集進行一系列拓展，先后提出直覺模糊集[2]、type-2型和n-型模糊集[3]等。近年來，Torra[4]提出利用具有多重隸屬度的猶豫模糊集，可較好地兼顧決策者意見不一致和模糊源過多的情形，更適合表達決策偏好[5]。

目前，針對解決猶豫模糊多屬性決策問題的研究，主要有兩類決策分析方法。一類方法是考慮決策者行為是完全理性的，這類方法已取得較豐碩的研究成果[6～15]，大致可分為三種情況：一是基于距離測度的決策方法，以TOPSIS和VIKOR等方法為典型代表。Xu等[6]研究以若干精確值和區間值表示隸屬度的猶豫模糊TOPSIS決策方法，利用歐幾里德距離測度各備選方案到正負理想點的相對貼近度，并依據相對貼近度的大小實現方案排序。然而，Xu等[6]選用的距離測度公式并未考慮猶豫模糊元中元素的不同隸屬程度。Liao等[7]和Zhang等[8]進一步拓展VIKOR決策方法在猶豫模糊環境的應用。Zhang等[9]提出基于標記距離的QUALIFLEX猶豫模糊決策方法。二是基于集成算子理論的決策方法。Xu等[10]提出一系列猶豫模糊集成算子，并探討算子間的相互關系。Yu[11]和Wu等[12]分別提出猶豫模糊Choquet平均算子和廣義猶豫模糊Bonferroni算子，并應用于多準則決策問題。三是基于方案兩兩比較的決策方法。Chen等[13]提出基于級別優先關系的猶豫模糊ELECTRE決策方法。王堅強等[14]提出猶豫模糊語言Hausdorff距離公式，并建立基于優序關系的猶豫模糊語言多屬性決策模型。于倩等[15]研究了基于ELECTRE方法的區間猶豫模糊多屬性決策問題。

另一類方法是考慮決策者行為是有限理性，這類方法主要是基于前景理論展開[16,17]。Zhang等[16]提出一種基于前景理論的交互式TOMID猶豫模糊多屬性決策方法。譚春橋等[17]將證據理論和前景理論相結合，提出一種基于證據-前景理論的猶豫-直覺模糊語言多準則決策方法。

上述研究成果極大豐富了猶豫模糊多屬性決策的理論與方法，從已有研究成果看，大部分研究僅適用于以精確值或區間值表示隸屬度的猶豫模糊決策方法。然而，在實際決策中，考慮到決策環境的復雜性、決策者認知的局限性和時間等限制因素，決策者往往難以給出以精確值表示的隸屬度；而以區間值表示隸屬度，由于區間值缺少中心，經過一系列復雜運算后很可能進一步擴大或縮小區間取值范圍。為克服這一缺陷，Wei等[18]提出三角猶豫模糊集，采用若干間的三角模糊數表示隸屬度，可以有效避免原始信息缺失，處理某些現實決策問題時更加便捷有效[18～21]。Wei等[18]提出一系列三角猶豫模糊平均算子，包括三角猶豫模糊加權平均(HTFWA)和三角猶豫模糊加權幾何(HTFWG)算子等。Zhao等[19]將Einstein運算引入三角猶豫模糊決策分析中，建立基于三角猶豫模糊加權平均(HTFEWA)和三角猶豫模糊加權幾何(HTFEWG)算子的決策模型。Zhong等[20]提出三角猶豫模糊Choquet有序平均(HTFCOA)算子，處理屬性間關聯影響的決策問題。梁邦龍等[21]建立基于三角猶豫模糊加權Bonferroni(HTFWBM)算子的決策模型。

需要說明的是，上述關于三角猶豫模糊多屬性決策問題均建立在決策者完全理性的基礎上，在實際決策中，決策者對待收益和損失持有不同的心理態度，這實際上反映決策者心理行為特征對決策的影響。因此，考慮如何將決策者心理行為特征引入三角猶豫模糊決策分析中，并給出相應方法是十分必要的。基于此，本文提出一種基于前景理論[22]和模糊結構元[23～25]的三角猶豫模糊決策分析方法。

1 基礎理論

1.1 三角猶豫模糊集

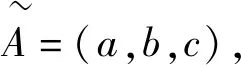
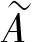
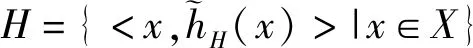
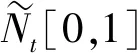
1.2 模糊結構元

定義4[23]設E為實數域R上的模糊集，其隸屬函數記為E(x)，x∈R。若E(x)滿足下述性質：

(1)E(0)=1；

(2)在區間[-1,0)上是單增右連續函數，在區間(0,1]上是單降左連續函數；

(3)當x∈(-∞,-1)或x∈(1,+∞)時，E(x)=0，則稱模糊集E為R上的模糊結構元。

若模糊結構元E滿足以下性質：

(1)對于?x∈(-1,1)，E(x)>0。

(2)在區間[-1,0)上是連續且嚴格單調增函數；在區間(0,1]上是連續且嚴格單調降函數，則稱模糊集E為正則模糊結構元。若E(x)=E(-x)，則稱模糊集E為對稱模糊結構元。

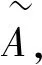
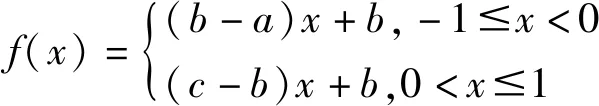
及對于模糊結構元E，其隸屬函數E(x)為：

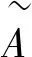
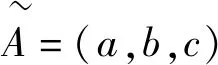
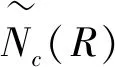
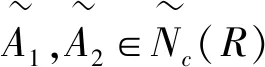
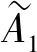
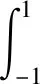
結構元加權序不僅考慮模糊數承集元素的大小關系，還綜合考慮元素的隸屬程度，即隸屬程度較大的元素在比較中起更重要的作用[25]。

1.3 前景理論

前景理論[22]以決策者有限理性為前提，能夠較好地刻畫決策者的心理行為特征。前景價值函數是決策者根據實際收益或損失產生的主觀感受，定義如下：

其中，Δx為偏離某一指定參考點的程度，若Δx≥0，表示決策者的心理感受為收益；若Δx<0，表示決策者的心理感受為損失。α，β為決策者的風險態度，且0<α，β<1 ，α和β越大，表明決策者越傾向風險尋求；θ為決策者對待損失的風險規避態度，θ>1，表示相對收益而言，決策者對待損失更敏感。

前景理論的核心思想是決策參照點的選定，在實際決策中，可考慮將正負理想點作為決策參照點。決策者將屬性值超過負理想點的部分視為收益；而將屬性值低于正理想點的部分視為損失，且對待收益和損失分別持不同的風險尋求和風險規避態度，這實際上體現決策者心理行為對決策結果的影響。

2 三角猶豫模糊元的結構元形式和距離公式

2.1 三角猶豫模糊元的結構元形式

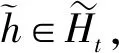
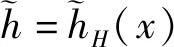
=H{f1(E),f2(E),…,fl(E)}

=H{fλ(E)|λ=1,2,…,l}

(1)

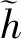
2.2 三角猶豫模糊元的海明距離

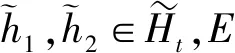
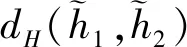
(2)

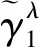
這里，式(2)是由定義5的結構元加權序誘導出。容易證明，式(2)滿足下述性質1。

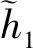
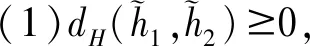
3 前景理論下的三角猶豫模糊決策方法

考慮含有三角猶豫模糊信息的多屬性決策問題，具體描述如下。

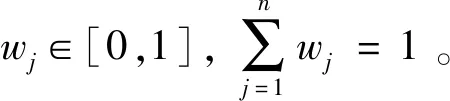
Step1構造標準化三角猶豫模糊決策矩陣M=(hij)m×n。

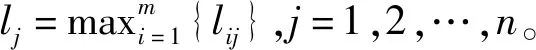
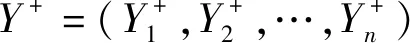
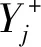
(3)

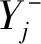
(4)

其中，j=1,2,…,n，lj為第j項屬性的長度。

Step3依據式(1)計算標準化屬性值的結構元形式，計算公式為：

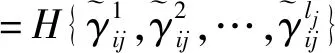
(5)

其中，i=1,2,…,m，j=1,2,…,n，lj為第j項屬性的長度。

Step4構建優化模型，確定屬性權重。

在屬性權重信息完全未知的情況下，文中利用離差法[29]確定屬性權重，即通過求解屬性間距離離差最大化的優化模型計算權重。該方法的核心是利用距離公式計算某一屬性下所有備選方案的離差值，該值越大，表示該屬性對備選方案的排序起較大作用，則應賦予較大權重；反之，若某一屬性關于備選方案的離差值很小，表示該屬性對決策方案的排序基本不起作用，則可令其權重為0。

首先，構造距離離差最大化的優化模型為：

(6)

其中，dH(hij-hkj)為hij和hkj的海明距離，由式(2)確定。

進一步，為求解上述優化模型，需構造拉格朗日函數：

(7)

其中，L(w,ξ)是拉格朗日函數，ξ為實數，表示拉格朗日乘子變量。對式(7)求偏導：

求解上述方程組得：

(8)

方便起見，對式(8)作歸一化處理，得最優權重為：

(9)

依據式(9)計算屬性權重向量w=(w1,w2,…,wn)T。

Step5依據式(2)計算標準化屬性值到正理想點和負理想點的距離，計算公式為：

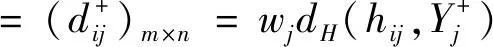
(10)

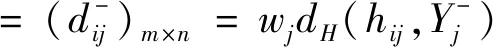
(11)

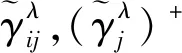
Step6分別構造收益矩陣和損失矩陣，計算公式為：

(12)

(13)

其中，i=1,2,…,m，j=1,2,…,n，α，β和θ分別為給定參數[22]。

需要指出的是，在實際決策中，依據前景理論，若以負理想點作為決策參照點，則構造收益矩陣，如式(12)所示；若以正理想點作為決策參照點，則構造損失矩陣，如式(13)所示。

Step7應用TOPSIS方法，計算各備選方案的相對貼近度，計算公式為：

(14)

其中，若Ci(i=1,2,…,m)越大，說明方案Yi越遠離負理想點，接近正理想點，則方案Yi越優。因此，可依據Ci值的大小對備選方案進行排序和優選。

4 算例分析

4.1 基于前景理論的三角猶豫模糊決策方法

為驗證本文提出方法的正確性和有效性，引用文獻[19]的算例進行驗證和分析。

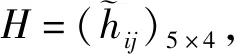
Step1構造標準化三角猶豫模糊決策矩陣M=(hij)5×4。設決策者為風險厭惡型，則選擇重復添加三角猶豫模糊元中最小的模糊數至該屬性長度相等[27]。則構造標準化三角猶豫模糊決策矩陣，如表2所示。

Step2依據式(3)和(4)計算標準化決策矩陣的正負理想點，計算結果如下:

Y+=(H{(0.7,0.8,0.9)},

H{(0.7,0.8,0.9),(0.8,0.9,1.0)}

H{(0.4,0.5,0.6),(0.6,0.7,0.8)}

H{(0.5,0.6,0.7),(0.5,0.6,0.7),

(0.6,0.7,0.8)})

Y-=(H{0.3,0.4,0.5},H{(0.2,0.3,0.4),(0.2,0.4,0.5)},

H{(0.1,0.2,0.3),(0.1,0.2,0.3)},

H{(0.2,0.3,0.4),(0.2,0.3,0.4),(0.2,0.3,0.4)})

Step3依據式(5)計算表2中標準化屬性值hij(i=1,2,3,4,5,j=1,2,3,4)結構元形式，例h11=H{(0.4+0.1E)}，h12=H{(0.7+0.1E),(0.8+0.1E)}。其他標準化屬性值結構元形式的計算方法依此類推。

Step4由于屬性權重信息完全未知，依據式(9)計算權重向量，則w=(0.2255,0.3154,0.2661,0.1930)T。

Step5依據式(10)和(11)計算標準化屬性值到正負理想點的距離，計算結果如下：

表1 三角猶豫模糊決策矩陣

表2 標準化三角猶豫模糊決策矩陣

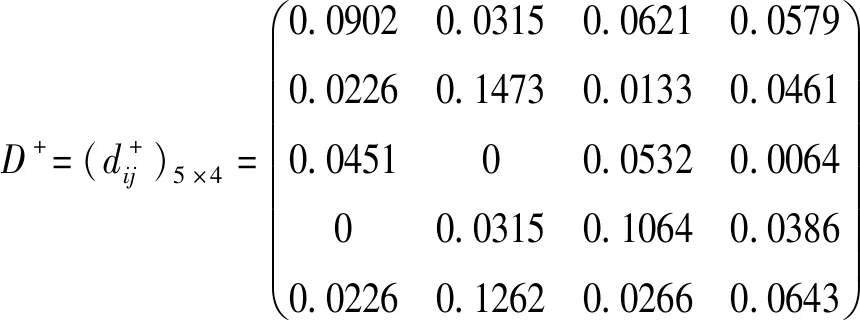
Step6依據式(12)和(13)分別構造收益矩陣和損失矩陣，計算結果如下：

其中，α=β=0.88，θ=2.25[22]。

Step7依據式(14)計算各備選方案的相對貼近度為C1=0.1951，C2=0.2932，C3=0.6008，C4=0.3285，C5=0.2553。因此，確定供應商的排序為Y3?Y4?Y2?Y5?Y1，最優供應商為Y3。

4.2 對比分析

為驗證本文方法的正確性，與文獻[16,18,19]的決策方法進行對比分析，排序結果見表3。比較分析以上不同方法可得結論如下：

(1)根據文獻[6]區間猶豫模糊海明距離公式，給出三角猶豫模糊海明距離為：

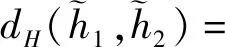
(15)

利用TOPSIS方法得到備選方案排序與本文方法略有不同，主要原因為：一是文獻[6]的方法僅以備選方案到正負理想點的距離作為決策尺度，并未考慮決策者對待收益和損失持有相同的風險偏好。而本文方法充分考慮決策者心理行為特征對決策的影響，放大決策者面對收益和損失的風險偏好，本文方法更符合決策實際。二是文獻[6]利用的距離公式，并未考慮猶豫模糊元中元素的不同隸屬程度，而本文方法通過結構元序誘導出的海明距離，不僅實現三角模糊數元中元素承集的大小比較，還考慮元素的不同隸屬程度，簡潔地實現三角猶豫模糊元的排序和選擇問題，避免決策信息缺失，計算過程更科學客觀。

(2)使用基于集成算子方法進行決策時，與本文方法相比，得到方案排序順序略有不同。主要原因在于文獻[18,19]的集成算子方法均是建立在決策者完全理性基礎上，并未考慮決策者心理行為對決策結果的影響。而本文方法充分考慮決策者心理行為特征對決策的影響，顯然本文方法更符合決策實際。此外，文獻[18,19]得到備選方案的綜合評價值均為三角模糊數，需選擇相應方法[28]實現模糊數的排序，決策結果具有一定主觀性和不確定性。

表3 基于不同方法的方案排序結果

5 結論

本文提出一種基于前景理論與模糊結構元的三角猶豫模糊多屬性決策分析方法。首先，給出三角猶豫模糊元的結構元形式，并通過結構元加權序誘導出三角猶豫模糊元海明距離公式，進而將三角猶豫模糊元的復雜變換關系轉化為上同序單調有界函數的運算，簡化其運算和變換，避免有效信息缺失，為猶豫模糊元的比較和排序提供一條有效途徑。其次，將前景理論引入三角猶豫模糊決策分析，克服傳統多屬性決策方法完全理性的缺陷，考慮決策者面對收益和損失時具有不同的風險偏好，符合人類本身非理性的決策模式。

運用本文方法，不僅能夠較好地處理與融合決策過程的三角猶豫模糊信息，同時決策結果有效反映決策者的心理行為特征，為進一步利用模糊結構元理論處理猶豫模糊多屬性決策問題并應用至其他模糊決策領域開拓了新思路。