考慮布局熵的多態性車間布局穩健優化模型與算法

陳 勇 程子文 姜樅聰 王亞良 王 成 酈仕云

浙江工業大學機械工程學院，杭州，310014

0 引言

制造業的市場需求有著持續性、關聯性、多變性等特點，客戶需求多樣化和訂單動態波動的趨勢日益突顯，企業需要更加合理的車間布局來滿足生產高柔性、制造低碳化、布局高穩定性等要求。復雜性作業車間的布局問題近年來的研究主要集中于面積利用率、物流成本、搬運距離、設備利用率、魯棒性和柔性等多目標對布局系統的影響。 朱琳等[1]為解決多品種混合裝配車間的布局問題，以工人平均取料路徑最短為目標，以物料擺放位置為決策變量，建立了數學模型，采用只允許最優解釋放信息素的蟻群算法求解目標函數；劉瓊等[2]針對動態環境下頻繁的布局優化，以物料搬運費用和面積費用最小化為目標，建立了魯棒性布局優化模型，利用改進的蛙跳算法求解具有較高魯棒性的布局方案；馬淑梅等[3]考慮產品不確定性隨時間變化的特性，構建了基于柔性區域結構的不確定需求動態布局模型，并提出一種結合模糊理論與改進遺傳算法的動態布局方法；劉瓊等[4]以制造過程總碳排量和調度完工時間最小為雙目標，建立了車間布局與調度集成優化模型；陳勇等[5]針對一類多態性作業車間，利用成組技術與分層思想構建低熵布局模型，提出了低熵化布局評價指標；GONZALEZCRUZ等[6]以多產品工藝順序作為設備間物流紊亂度指標，采用熵優化算法求解了混合生產車間低紊亂度布局問題；KAVEH等[7]通過建立期望值、機會約束規劃、相關機會規劃模型來解決模糊約束條件下的動態車間布局問題；GARCIAHERNANDEZ等[8]針對物流量最小和穩定性最高的多目標，設計了融合專家定性評判與聚類遺傳算法的混合優化算法；RAZAVIALAVI等[9]同時考慮設備位置、物流成本以及動態物料配送，建立了多目標布局模型，采用遺傳算法與仿真軟件的交互式運算解決了多態性車間布局問題；LENO等[10]以單元間設備布局、物料進出口最佳位置和物料移動距離為目標建立基于混合整數規劃的數學模型，通過最小化處理成本來評估布局的質量，設計融合模擬退火算法與遺傳算法的混合進化算法來求解目標。

在解決多目標問題時，多目標優化算法求解Pareto解集是主要趨勢。如非支配解排序遺傳算法(non-dominated sorting genetic algorithmⅡ,NSGAⅡ)[11]、強度Pareto進化算法(strength pareto evolutionary algorithm,SPEA)[12]等。近年來，又相繼出現了在NSGA基礎上改進的多目標粒子群算法(multi-objective particle swarm optimization,MPSO)[13]、多目標果蠅優化算法(multiobjective optimization algorithm for drosophila melanogaster，MOADM)、多目標差分元胞遺傳算法(multiobjective differential cellular genetic algorithm，MDCGA)[14]。總體而言，這些算法在一定程度上能夠很好地求得Pareto解，但也存在一些問題。如NSGAⅡ、SPEA會出現解集分布不均勻、收斂性不足等問題。改進的多目標算法整體上表現出良好的性能，但在非線性、高維度的NP-Hard問題上依然不能滿足要求。

本文提出以單位面積布置成本、單位產品物流成本以及布局熵為指標，設計多目標的布局模型，實現一類多態性車間低成本、高穩健性布局。設計基于Pareto優化的模糊聚類并行多目標遺傳算法以提高Pareto解集分布的多樣性與均勻性；提出改進的多元胞差分進化重插入操作以避免算法陷入局部最優。提出的算法能夠有效地保證整個Pareto曲面解集的均勻分布，保證種群的多樣性，提高進化效率與解的質量。

1 一類多態性作業車間布局目標

1.1 一類多態性作業車間問題描述

一類多態性作業車間是指大規模定制和產業集群下代工企業為滿足多品種、小批量的市場需求，以單元群制造模式為基礎，實現多產品、多工藝、多功能區域一體化的生產車間[15]。其生產過程在訂單、設備、工藝、批量、瓶頸等層次上越來越凸顯出形態和狀態的多樣性，加工批量和運轉批量呈現動態性，布局高穩健性需求逐步增強。

多態性作業車間布局問題描述如下：n種產品需要在m個功能單元內加工裝配，每種產品具有不同的加工路線，受到功能區域緊前關系約束，需要完整地在必須經過的功能單元上完成相應的過程。布局過程受單元形狀、物流成本、產品工藝、布局穩定性等多條件約束，需尋求車間布局整體最優化。

1.2 車間布局多目標

企業希望通過提高車間面積利用率，降低產品物流成本，同時保證車間的穩定性，實現車間的有效布局。參考文獻[16]給出的布局關鍵目標建議，提出以下3個布局目標。

(1)單位面積布置成本T。傳統意義上的車間面積利用率是需求面積與車間總面積之比，僅表示車間面積被占用情況，無法表征土地利用價值。筆者認為在有限的土地資源中，單位面積布置成本能夠更加直觀地體現車間面積的有效利用價值。單位面積布置成本越小，表明面積的利用價值越高，布局更合理高效。

考慮不同的設備布局方式會帶來單元形狀變化，進而引起布置成本變動，因此研究中考慮單元形狀不固定的情況，引入單元縱橫比的概念，即

(1)

式中，li、hi為單元i的長度和寬度。

對任意單元而言，恰當的縱橫比表征合理的單元形狀，不易引起額外的布置成本，否則易造成布置成本增加。將縱橫比與設備成本耦合，定義布置成本：

(2)

s.t.

Δx=max|xi-xj|

Δy=max|yi-yj|

i,j=1,2,…,m

式中，m為單元數；Mi為單元i的設備數；qM為設備M的成本；F(ηi)為單元縱橫比ηi模糊評價函數，參考文獻[17]，文中引用圖1所示的最簡單的評價函數；ηi,max、ηi,opt為單元i縱橫比上限和最優值，可根據實際情況定義；Δx、Δy分別為單元i、j沿x軸和y軸方向的間距；ΔxΔy為車間包含所有單元的最小面積；xi、xj、yi、yj分別為單元i、j的橫縱坐標。

(2)單位產品物流成本Z。最小化物流搬運耗費是傳統的布局評價目標。產品物流流向的復雜性與功能單元的不確定性導致常規的物流量距模型只能模糊地描述車間物流對布局的約束。多品種多工藝生產的路線較多、交叉頻繁，需根據不同產品組合選擇合理的生產工藝路線，以減少其交叉。同時考慮搬運距離，以達到總物流量距最小。筆者提出以單位產品的有效物流量距成本與路線交叉懲罰成本衡量物流對布局的約束，有

(3)

s.t.

dij=|xi-xj|+|yi-yj|

式中，n為產品總數量；fijp為產品p在單元i至單元j間的物流量；cijp為產品p在單元i和j之間的單位運輸成本；Cpk為產品p與產品k的路線交叉懲罰成本；dij為單元i和單元j間的距離，考慮車間內物料搬運無法沿兩點間直線搬運，故視為單元間折線距離。

(3)布局熵E。多態性作業車間需要一個較為穩定的生產環境，穩定性的獲得不僅依賴于布局系統的可靠運行，同樣依賴于布局系統單元間各種關聯關系的相對穩定性。本文引入熱力學中象征系統紊亂度的物理熵概念，根據熵的含義，布局自然發展的過程為在自組織作用下熵值不斷增大的過程，即系統紊亂度增加。由于熵值的增大導致布局系統復雜性增加，從而降低了效率，因此需要給出低熵化、引導性的布局約束。基于脆弱性抽象的布局熵模型以物理熵為車間穩健優化度量指標，能很好地滿足系統高穩定性、持續改善的要求。

根據文獻[18-19]所述，由某種相似粒子組成的系統，N和Es分別表示系統中粒子的數量和其所擁有的能量，系統某一時刻處在微觀狀態(N，Es)的概率為

(4)

式中，a、b為歸一化系數。

由物理熵表達公式可知系統的熵值表達式：

(5)

研究過程中將車間視為一個無序的開放系統，單元設備、物料等視為系統粒子。衡量布局熵的關鍵在于如何定義概率P，根據物理熵公式的含義及其單調性可知，概率P越大，熵值越小，系統越穩定。考慮車間布局實際情況，將P定義為車間某種狀態可能崩潰情況的映射概率。布局魯棒性能差則無法應對車間機器故障等不確定性因素，柔性程度低則無法及時應對多生產工藝路線更改等擾動因素，兩種情況都有可能導致車間停產崩潰。因此將各種引起崩潰的情況綜合為魯棒性與柔性兩種，建立概率P與魯棒性(R)和柔性(F)的映射關系，以布局熵反映車間紊亂度，能夠很好地表征布局系統的穩定程度。

對布局層面而言，產品工藝魯棒性體現在加工距離差異性上。不同產品的工藝路線與加工距離各不相同，保證加工距離的一致性能夠保證生產穩定性，即

(6)

s.t.

式中，Lp為產品p經過完整工藝路線的加工距離；wp為產品p的工序集合；I(J)表示第I(J)道工序。

布局柔性體現布局系統自身調節能力，主要影響因素有生產路徑、物流量、可變單元數、單元負載量等。布局柔性定義為

(7)

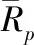
建立概率P與魯棒性R和柔性F的映射模型：

(8)

(9)

其中，Rmax、Rmin、Fmax、Fmin分別為理論上魯棒性和柔性的最大值、最小值；考慮到布局實際與概率映射模型，崩潰概率P∈(e-1,1)，魯棒值R越大，則車間穩健性能越好，崩潰概率P1越小；柔性程度越高，則車間容納性能越好，崩潰概率P2越小。

在式(8)、式(9)基礎上建立表征車間布局穩定程度的布局熵模型：

E=e·(P1lnP1+P2lnP2)+1

(10)

由式(10)的單調性可知，崩潰概率越小，熵值E越小，車間穩定性能越好。為了將E映射至(0,1)區間，參考文獻[5]，取E∈[0.2,0.8]，認為在此區間布局系統的熵值合理。

1.3 車間布局多目標優化模型

筆者提出的單位面積布置成本、單位物流成本以及布局熵3個目標之間存在著相互競爭的關系：單位面積布置成本越高，單元分布越緊湊，物流量距越小，工藝路線交叉越頻繁，直接引起車間布局熵增加。因此建立多目標優化模型，利用改進的多目標求解算法求解Pareto解集，模型如下：

(11)

(12)

f3=min(e·(P1lnP1+P2lnP2)+1)

(13)

1.4 約束條件

將車間看作一個二維矩形平面，各功能單元為矩形，平面內以車間左下角為原點建立長寬方向的坐標系，如圖2所示。因本文編碼方式存在邊界約束性，因此只需建立位置約束：

(14)

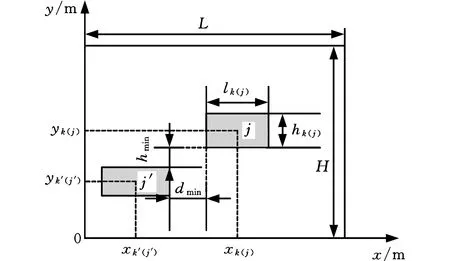
圖2 車間坐標示意圖Fig.2 Workshop coordinate diagram

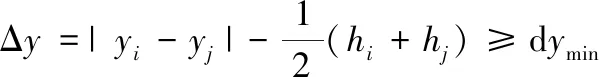
(15)

式中，dxmin、dymin為沿x軸和y軸方向的最小間距，用來保證任何兩個單元不會重疊布置。

2 算法設計

針對多目標車間布局問題，提出基于Pareto優化的聚類并行多目標遺傳算法(cluster parallel multi-objective genetic algorithms，CPMGAs)，在每一代進化過程中得到的當前種群中引入模糊C-均值聚類算法，依據布局模型的多個優化目標將種群分成n類元胞種群，元胞種群存在組內染色體相似度最高、組間染色體差異性最大的特征，該進化過程可以提高Pareto解集分布的多樣性與均勻性；提出改進的多元胞差分進化重插入操作，并采用“移民策略”避免算法陷入局部最優[20-21]。提出的算法能夠有效地保證整個Pareto曲面解集的均勻分布，保證種群的多樣性。改進的多元胞差分進化重插入操作與移民策略能起導向進化作用，保證優質解的有效遺傳，提高進化效率。

2.1 CPMGAs基本框架

引入模糊C-均值聚類算法，依據各目標將種群劃分為若干元胞種群，并組成環狀拓撲結構進行協作進化，以增強種群的導向性進化，基本框架如圖3所示。

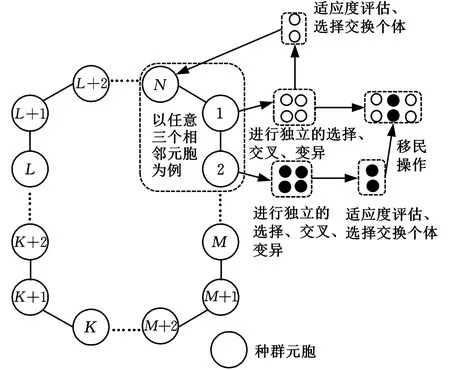
圖3 CPMGAs模型框架Fig.3 Framework model of CPMGAs

2.2 染色體編碼策略

根據布局模型，染色體需要包含三類信息：單元坐標、形狀和組合分布情況。為避免編碼冗長,采用FBS(flexible bay structure)編碼方式：每條染色體由單元排序編碼與單元分割點編碼兩部分組成。單元排序編碼由n個單元組成，表示車間由左至右，從上至下排列順序；分割點編碼由n-1個0/1二進制編碼組成，0表示單元處于同一縱列，1表示單元為某縱列最后單元。

為方便編碼與計算，對車間單元和編碼環境作如下簡化：

(1)研究的單元是包括機器群、通道、緩沖區等組成的綜合單元模塊，單元面積確定，形狀可變。

(2)FBS編碼前，總面積的長與寬已知，即各單元填充排布的總區域是確定的，如圖4所示，即

LH=SA+SB+SC+SD+SE+SF

其中，L、H為已知單元填充區域的長與寬；SA為單元A的面積，其余解釋同SA。

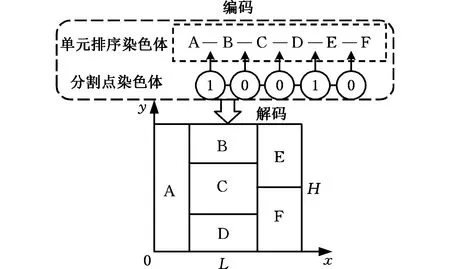
圖4 FBS編碼方式示意圖Fig.4 FBS encoding scheme diagram

FBS編碼過程確定了各單元間的相對位置，接下來根據L、H及各單元面積確定精確位置坐標。由FBS編碼規則可知，單元A的左下角為直角坐標系原點處，具體求解步驟如下(以圖4為例)。

(1) 單元A的寬度已知，即hA=H，長lA=SA/hA，則單元A的坐標(xA，yA)=(SA/(2hA)，H/2)。

(2)計算第二列單元坐標。由于lB=lC=lD，SB/lB+SC/lC+SD/lD=H，因此lB=lC=lD=(SB+SC+SD)/H，hB=SBH/(SB+SC+SD)，hC=SCH/(SB+SC+SD)，hD=SDH/(SB+SC+SD)。則第二列各單元坐標：(xD，yD)=(lA+(SB+SC+SD)/(2H)，hD/2),(xC，yC)=(lA+(SB+SC+SD)/(2H)，hD+hC/2),(xB，yB)=(lA+(SB+SC+SD)/(2H)，hD+hC+hB/2)。

(3)依次計算剩余單元的坐標。

(4)根據式(14)、式(15)，排除不符合約束的染色體，如兩長度足夠小且相鄰的單元，其單元間距有可能不滿足位置約束。

在FBS編碼前提下計算精確位置，能夠最大限度地減少不滿足間距約束的染色體生成，提高編碼的效率與有效性。

2.3 模糊聚類操作

與傳統聚類算法對數據的硬劃分不同，模糊聚類是依據多個聚類特征的綜合隸屬度進行聚類，是一種分類界限模糊化處理的軟劃分[22]。由于布局問題復雜多變，故允許同一布局方案(染色體)同時處于多個分類，避免算法陷入局部最優陷阱。參考GARCIAHERNANDEZ等[8]提出的聚類方法，引入模糊C-均值聚類算法，算法模型如下：

(16)

s.t.

(17)

(18)

(19)

式中,FC為聚類目標函數，用來衡量聚類特征綜合相異程度；V為數據個數;K為聚類中心的個數;g為聚類特征類別;z為聚類特征;vr為第r個數據;ch為模糊組h的聚類中心;urh(v)為隸屬度函數，表示第r個數據點隸屬于第h個聚類中心的程度;vrg為以特征g為分類指標時的第r個數據;chg為以特征g為分類指標時模糊組h的聚類中心；z為聚類特征個數，以單位面積布置成本、單位產品物流成本、布局熵為聚類特征，即z=3；f為大于1的模糊參數，取值為2。

圖5為初始種群模糊聚類為若干元胞種群示意圖。通過各染色體的單位面積布置成本、單位物流成本以及布局熵的值計算染色體隸屬度，并做劃分處理，得到的各種群存在內部相似性最大，種群間差異性最大的特點。

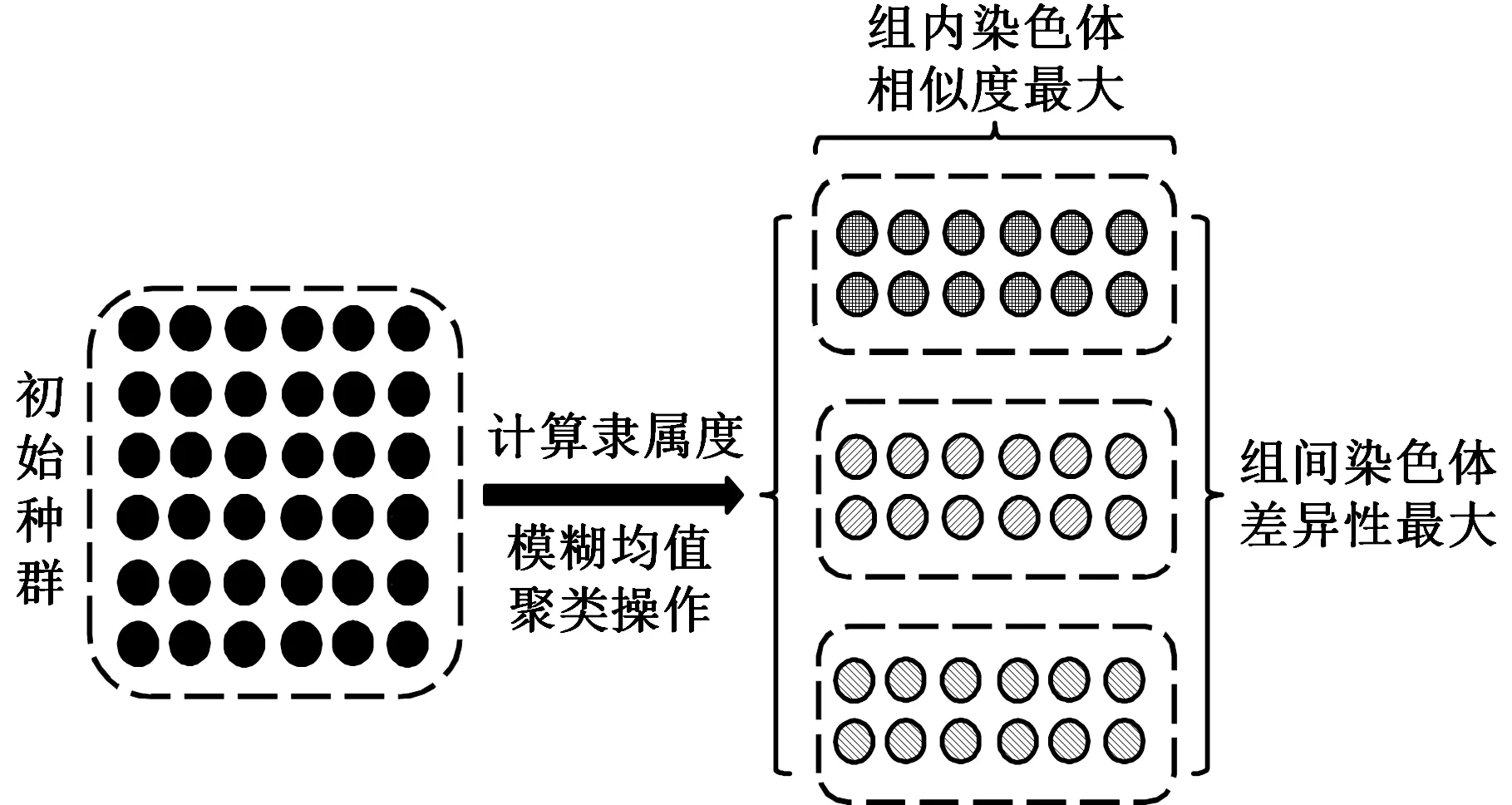
圖5 初始化種群元胞組合示意圖Fig.5 Initialized population cell assembly schematic

2.4 進化算子

選擇、交叉、變異的操作過程是同時在各自元胞種群中獨立完成的，這三步操作環境相對封閉，既能最大程度地保證各組特征的遺傳，也為元胞種群間的協作進化奠定基礎。

(1)選擇算子。選擇過程既要保證各自元胞種群特征的遺傳，也需要引導種群向最優Pareto解進化。本文采用錦標賽法，該方法是基于個體的秩與隸屬度對父代種群進行選擇的。步驟為：①根據個體的支配關系，對種群分層，確定個體的秩，第一層秩為1，依次遞增；②選出當前個體的鄰居個體，比較鄰居個體的秩，秩越小則個體性能越優秀，保留下來；③若與鄰居個體的秩相等，則比較它們的種群隸屬度，隸屬度越大的個體表明與中心個體性能越接近，保留。由①、②、③三步確定出優秀個體。

(2)交叉算子。根據編碼方式的特殊性，采用兩種不同的交叉算子進行交叉。針對單元排序部分，采用部分映射交叉算子可以有效地避免交叉后設備的重復性。針對單元分割點部分，采用多點交叉算子交換片段。

(3)變異算子。針對單元排序部分，為了避免變異后的單元排序中有重復單元編號，采用單元交換法：任意選取同一染色體兩個單元位，交換單元位置。針對單元分割點部分，采用基因位0-1轉換法：依據概率任意選擇基因位，將0轉換為1，將1轉換為0。

2.5 多元胞差分重插入操作

為保證子代染色體數量保持不變和種群多樣性，每一輪進化完成后需補充若干新個體進入種群池。多元胞差分利用各元胞中個體的距離與方向的優勢信息，具有全局并行搜索的優點。具體操作如下。

在第G+1代重插入開始之前，首先從3組元胞種群中各隨機選擇一個個體作為父代個體，記作f1，i(G)、f2，i(G)、f3，i(G)，i=1，2，…，f1，i(G)表示第i次重插入時從第G代種群的第1個元胞中隨機選擇的父代個體。判斷是否存在全局支配解。

(1)如存在全局支配解則將其定義為fbest，變異按下式規則操作：

fi(G+1)=αfbest+(1-α)(f1，i(G)+
F(f2，i(G)-f3，i(G)))

(20)

(2)若不存在全局支配解，則變異按下式規則操作：

fi(G+1)=f1，i(G)+s(f2，i(G)-f3，i(G))

(21)

式(20)表示取父代個體f2，i(G)、f3，i(G)的差值，將其縮放的結果直接加到個體f1，i(G)上獲得新個體，再將其與全局支配解進行交叉，獲得變異后的個體。α為貪婪因子(α∈(0,1))，α值越大，表示保留全局支配解的基因片段越多；s表示縮放因子，為一個確定的常數，s∈[0,1]；fi(G+1)表示第(G+1)代第i個變異個體。式(21)表示取父代個體f2，i(G)、f3，i(G)的差值，將其縮放的結果直接加到父代個體f1，i(G)上獲得新個體。

經測試，改進后的多元胞差分重插入操作充分利用了各優勢種群的全局非支配解集，確保優勢基因的遺傳，提高了解的質量。圖6為多元胞差分重插入操作示意圖。

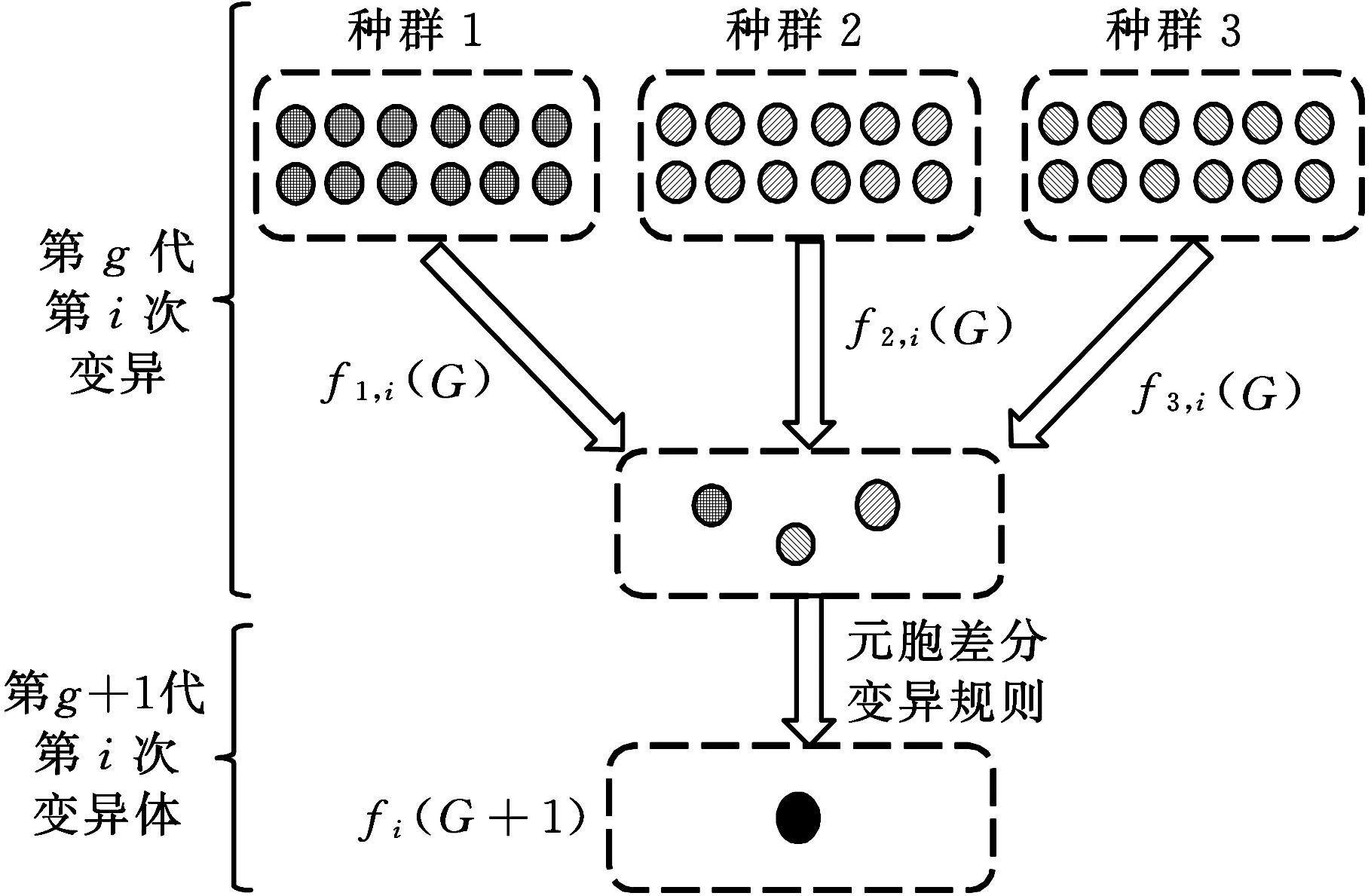
圖6 重插入操作示意圖Fig.6 Reinsertion operation schematic

2.6 移民策略

各元胞之間存在最大差異性，且各元胞內均有屬于自己的Pareto解，為使這些“精英染色體”得到最大程度的遺傳并對種群起到導向進化的作用，需在下一代進化開始之前，進行優秀個體的移民操作。具體如下：隨機排列元胞種群并連接組成環狀拓撲結構，為元胞間指定某種遷移拓撲，確定個體交換的方式。移民路徑如圖7所示，圖中,k1、k2、k3表示按比例從各組元胞種群中復制的優秀個體數量。

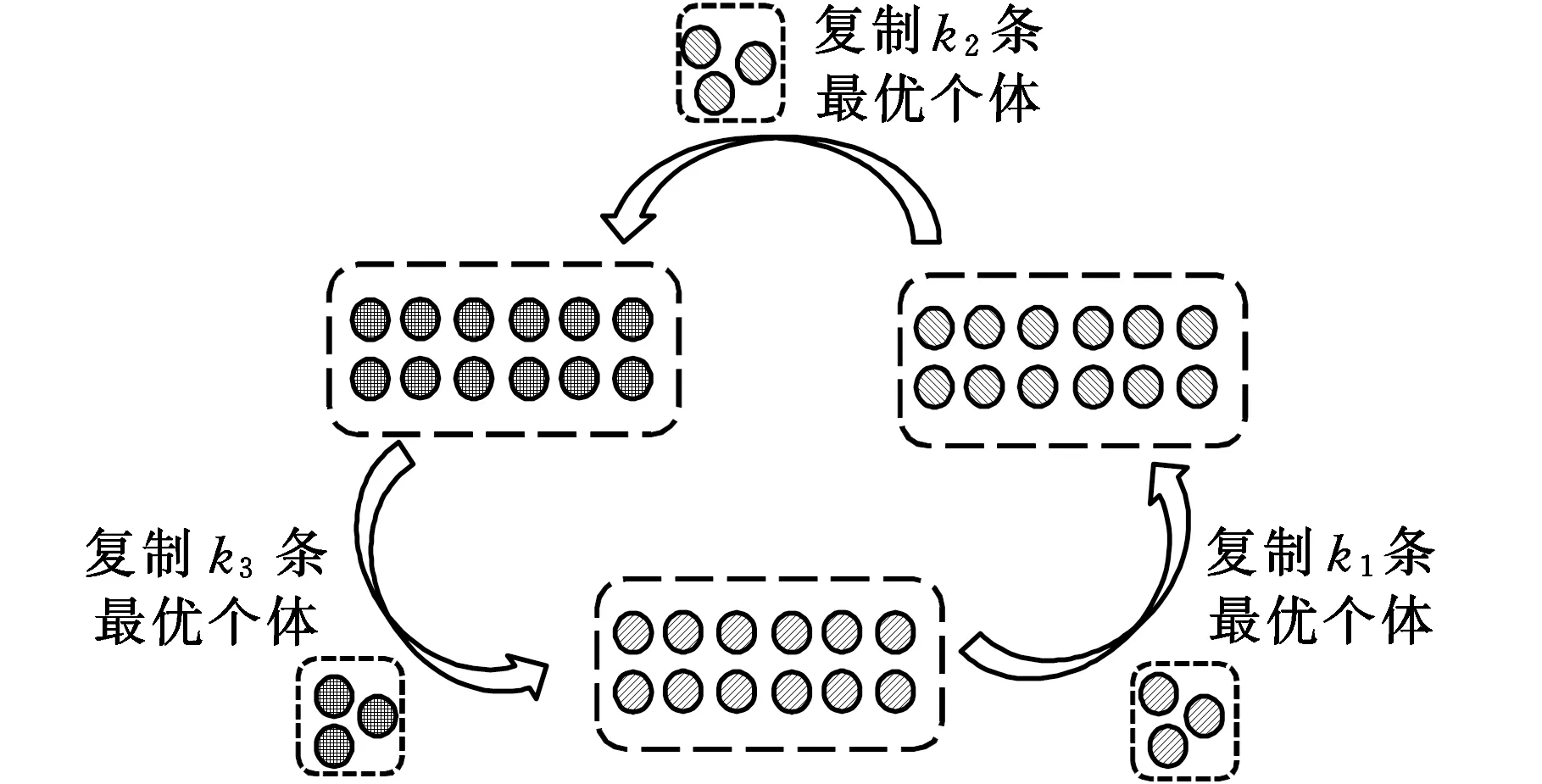
圖7 染色體移民示意圖Fig.7 Chromosome migration diagram

2.7 循環終止條件

循環執行模糊聚類、選擇、交叉、變異、移民等操作，算法迭代niter次或在迭代過程中連續mopt次產生PN條Pareto解集，則進化結束。

3 算法步驟與流程

算法流程如圖8所示。

(1)利用FBS編碼隨機產生一定規模的種群。

(2)計算所有染色體的f1、f2、f3的目標值，運用模糊C-均值聚類算法，對所有染色體聚類，分為PC組種群元胞，文中取PC=3。

(3)各元胞同時進行獨立的選擇、交叉、變異。

(4)重插入操作。按照多元胞差分操作規則，生成一定數量的新個體平均分配給各元胞。

(5)將各元胞組成環狀拓撲結構，對環狀鄰域種群元胞進行精英個體的移民操作。

(6)如果算法迭代niter次或在迭代過程中連續mopt次產生PN條Pareto解集則結束計算，輸出Pareto解集，否則返回步驟(2)，進行下一輪進化。

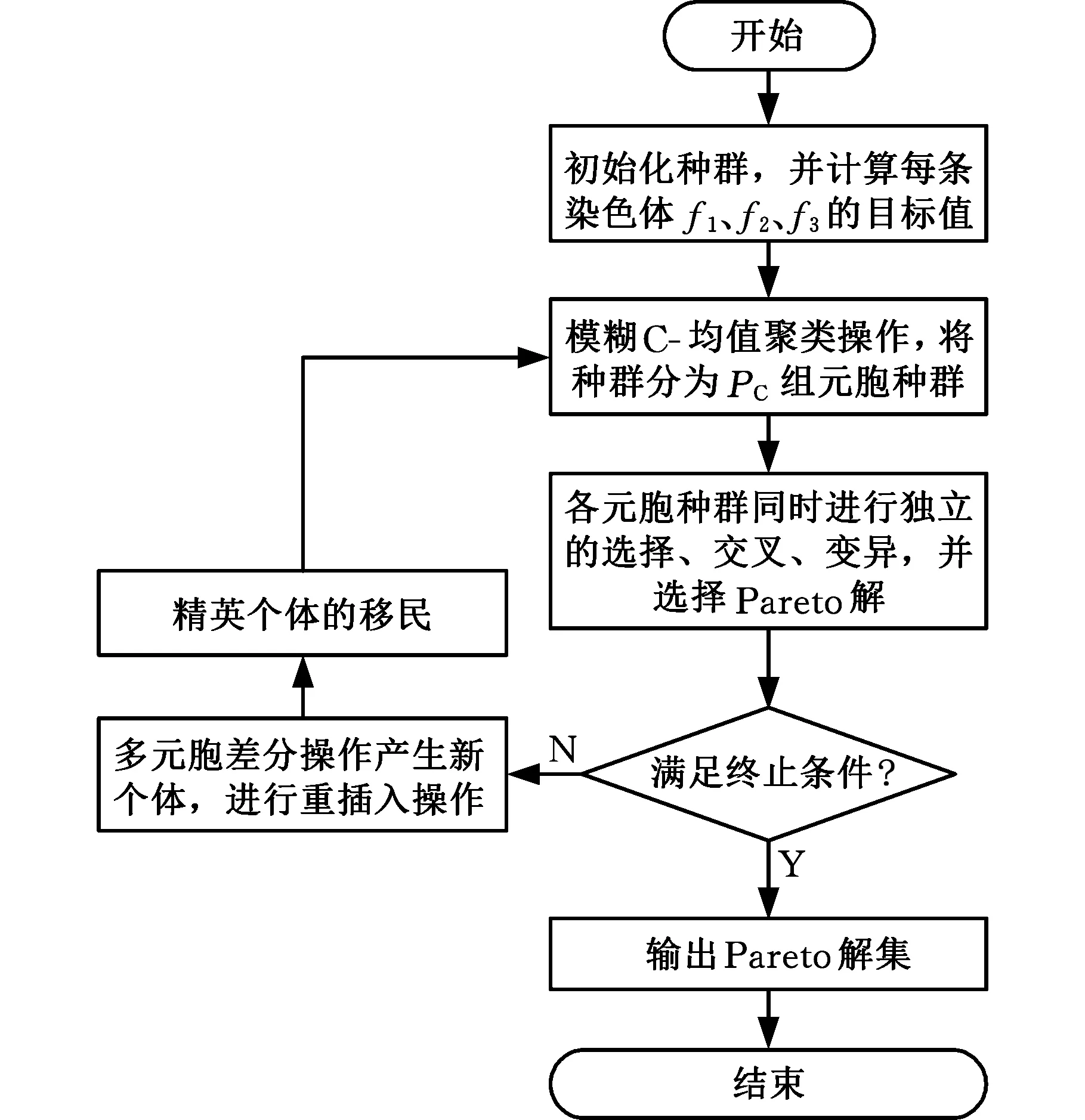
圖8 算法流程Fig.8 Algorithm flow

4 算法性能分析與算例驗證

為驗證本文算法的性能，選用一個多約束、多變量的雙目標測試函數ZDT3和一個高維多目標函數DTLZ2[23]，分別利用文獻[13]的MOPSO、文獻[14]的NSGAⅡ以及本文的CPMGAs對上述測試函數進行計算，并分析相同評價體系下三種算法的性能。

4.1 算法性能評價指標

采用分布指標[23]、世代距離和超體積指標對算法性能進行評價[24]。

(1)分布指標TD。分布指標用來衡量獲得的Pareto前沿的分布情況，該指標的值越小，表明Pareto前沿分布越均勻，且

(22)

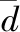
(2)世代距離GD。世代距離用來計算所得的Pareto前沿收斂到最優 Pareto前沿的程度，GD越小，解的收斂性越好,且

(23)

式中，n為近似Pareto前沿中個體的數目；di為第i個解的目標函數構成的向量與Pareto最優前沿之間的最近距離。

(3)超體積。超體積(HV)用來計算獲得的Pareto前沿在目標空間所覆蓋的體積。超體積越大，說明獲得的Pareto前沿的多樣性、收斂性越好，有

(24)

在三維目標空間中，Q表示所有Pareto解的個數，Vi是由參考點W與解i的目標向量作為對角點所形成的長方體的體積。為方便處理，將最差的分目標值構成的一個向量作為參考點W，合并所有Vi得到HV。

4.2 算法測試結果及性能分析

ZDT3與DTLZ2基準測試函數如表1所示。

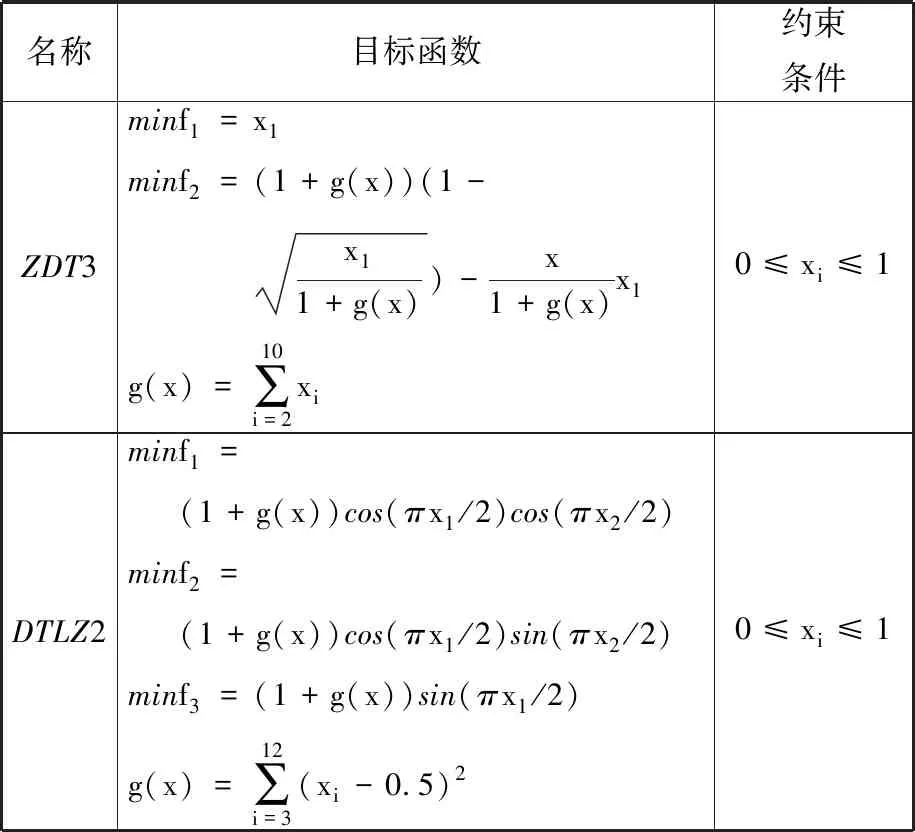
表1 ZDT3與DTLZ2基準測試函數Tab.1 ZDT3 and DTLZ2 benchmark functions

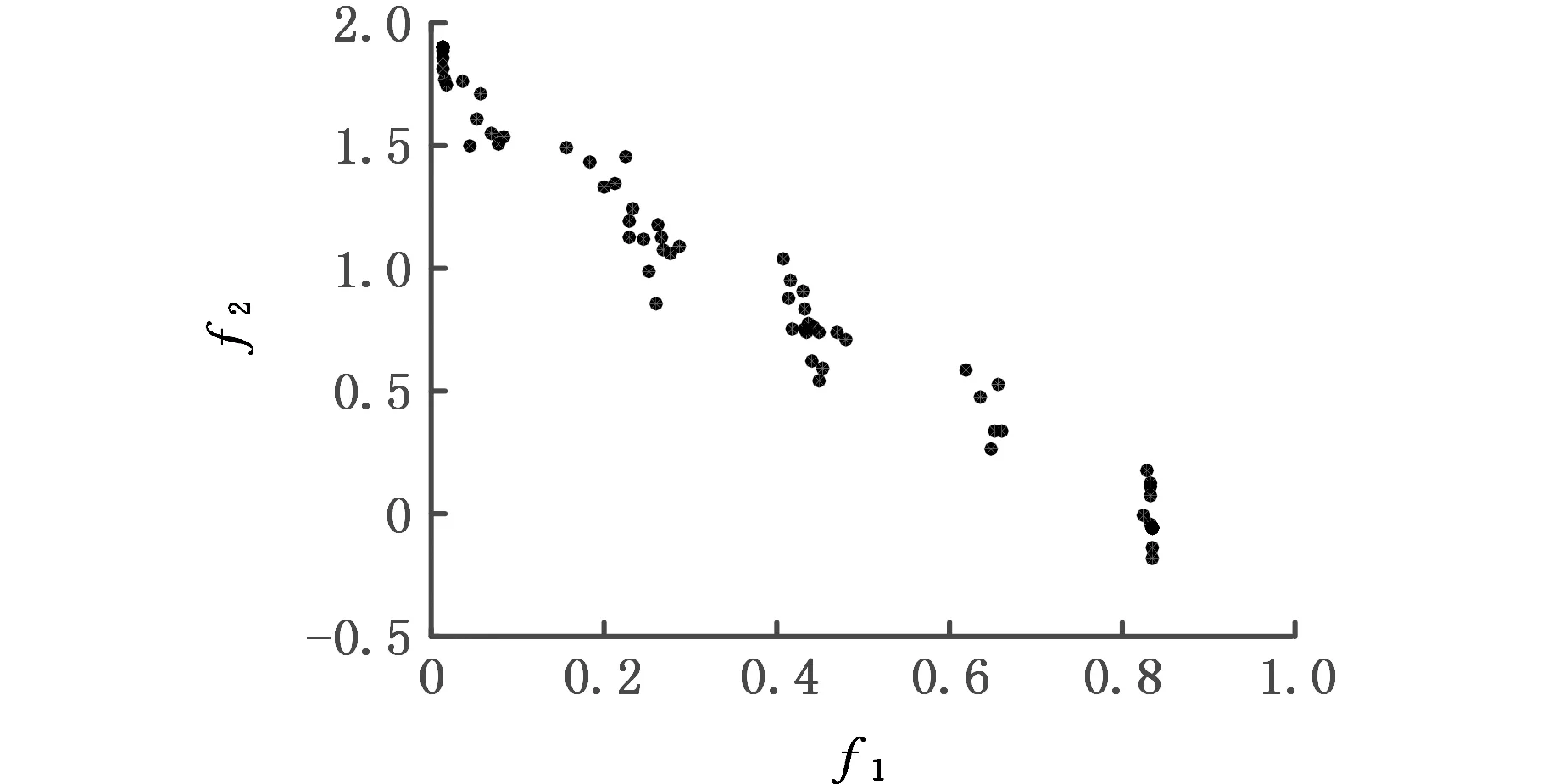
NSGA Ⅱ、MPSO、CPMGAs算法參數設置如下：均采用實數編碼，多項式變異；采用模擬二進制交叉；MPSO算法的學習因子均取0.8；CPMGAs的元胞種群分組取PC=3，移民率為各元胞的5%；交叉概率取0.8，變異概率取0.3，種群規模取100，進化代數為50。三種算法對測試函數ZDT3和DTLZ2均進行20次測試，表2表示三種性能指標統計結果均值。圖9、圖10分別表示測試函數ZDT3和DTLZ2的Pareto解前沿分布。

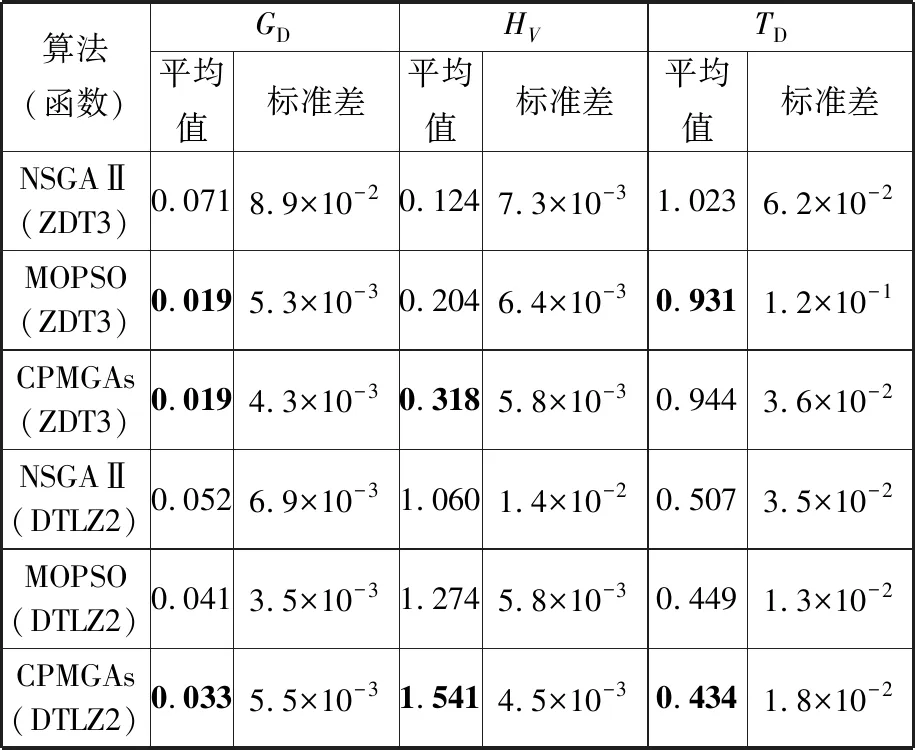
表2 算法有效性分析表Tab.2 Algorithm validity analysis table

(a)NSGAⅡ算法Pareto解集前沿

(b)MPSO算法Pareto解集前沿

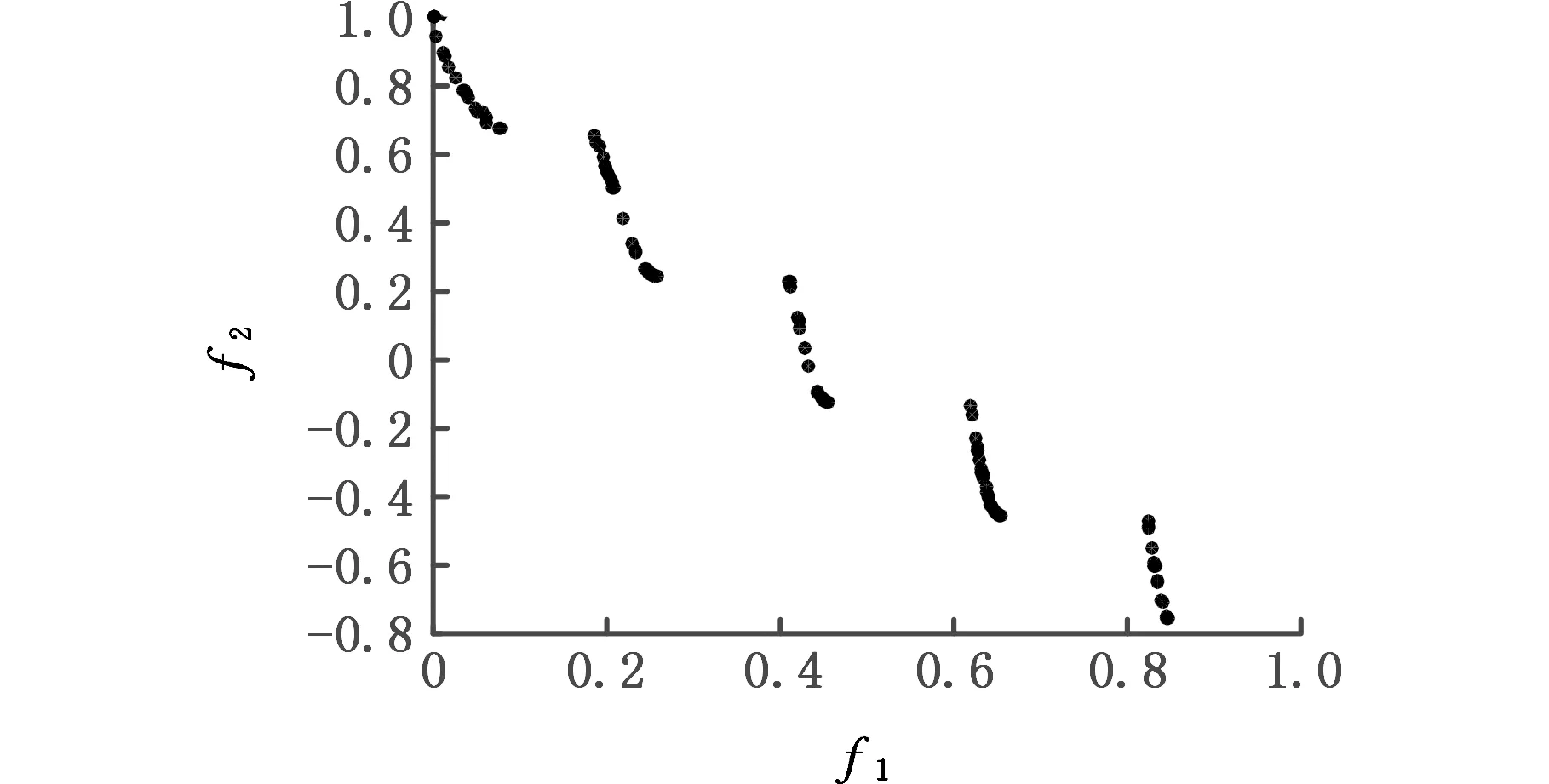
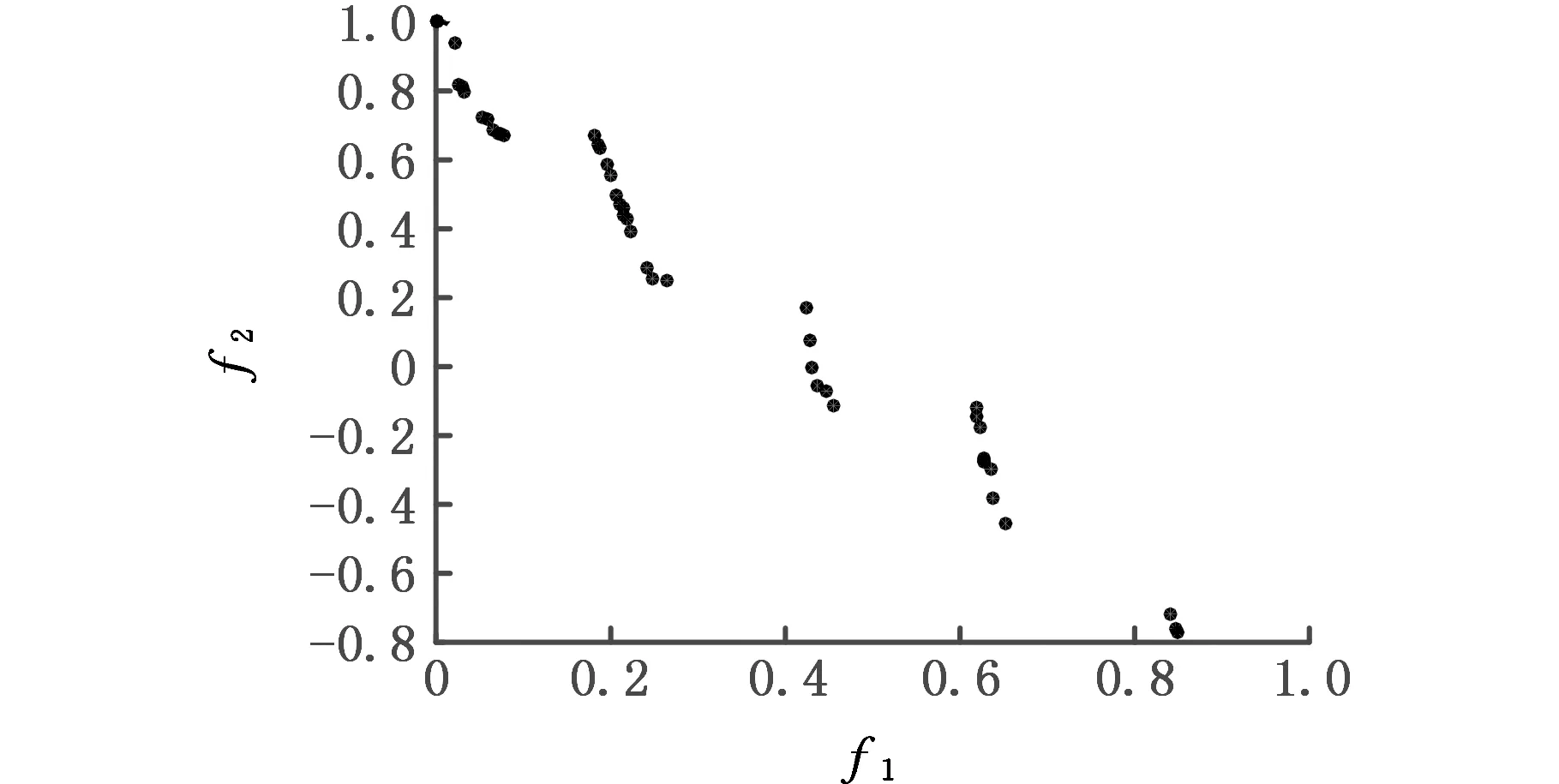
(c)CPMGAs算法Pareto解集前沿圖9 NSGAⅡ、MPSO、CPMGAs算法在ZDT3上的Pareto前沿對比圖Fig.9 Pareto frontier contrast diagram of NSGA Ⅱ、 MPSO、CPMGAs algorithm on ZDT3

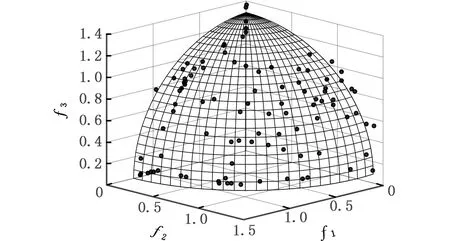
(a)NSGAⅡ算法Pareto解集前沿

(b)MPSO算法Pareto解集前沿

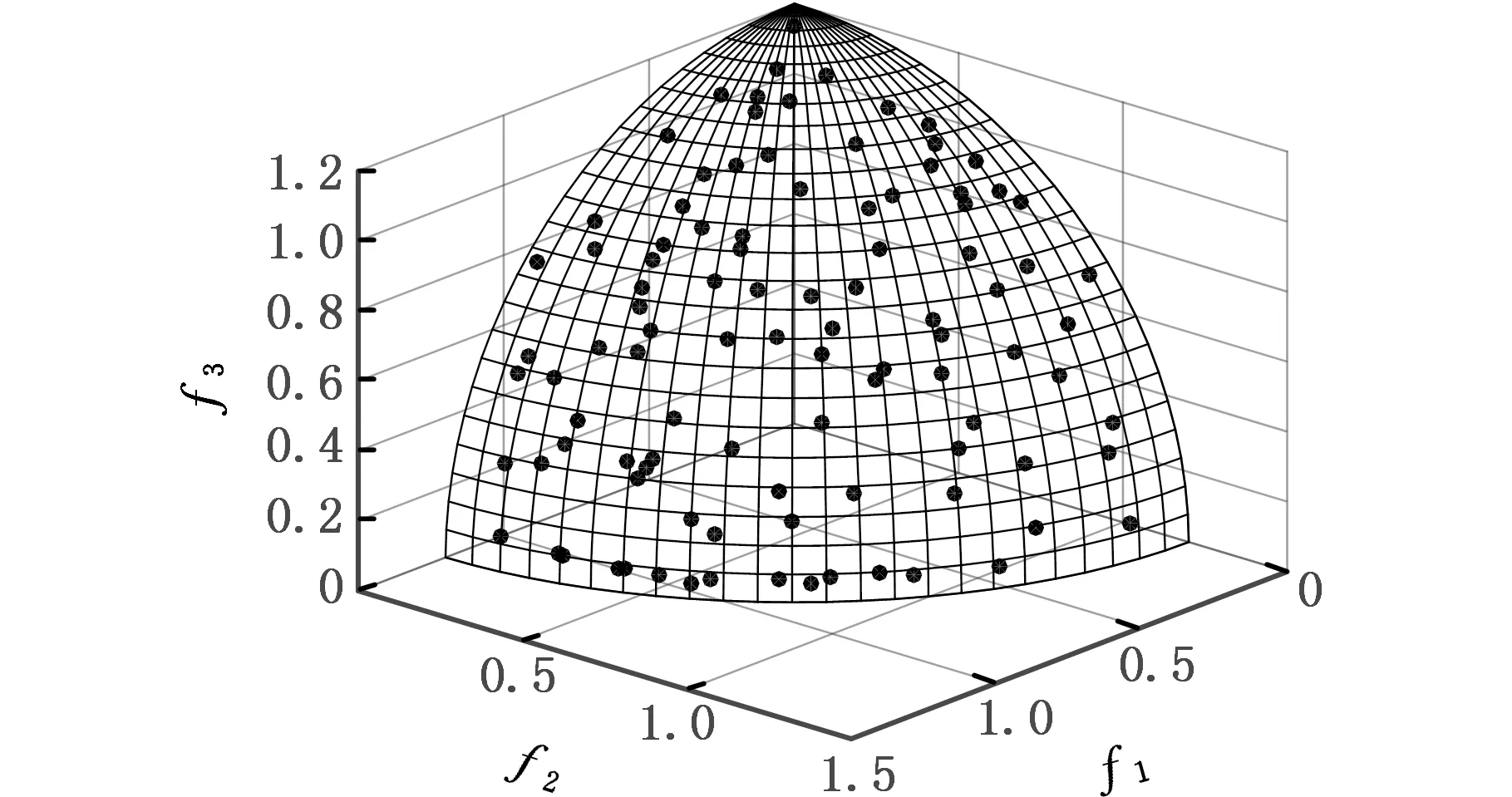
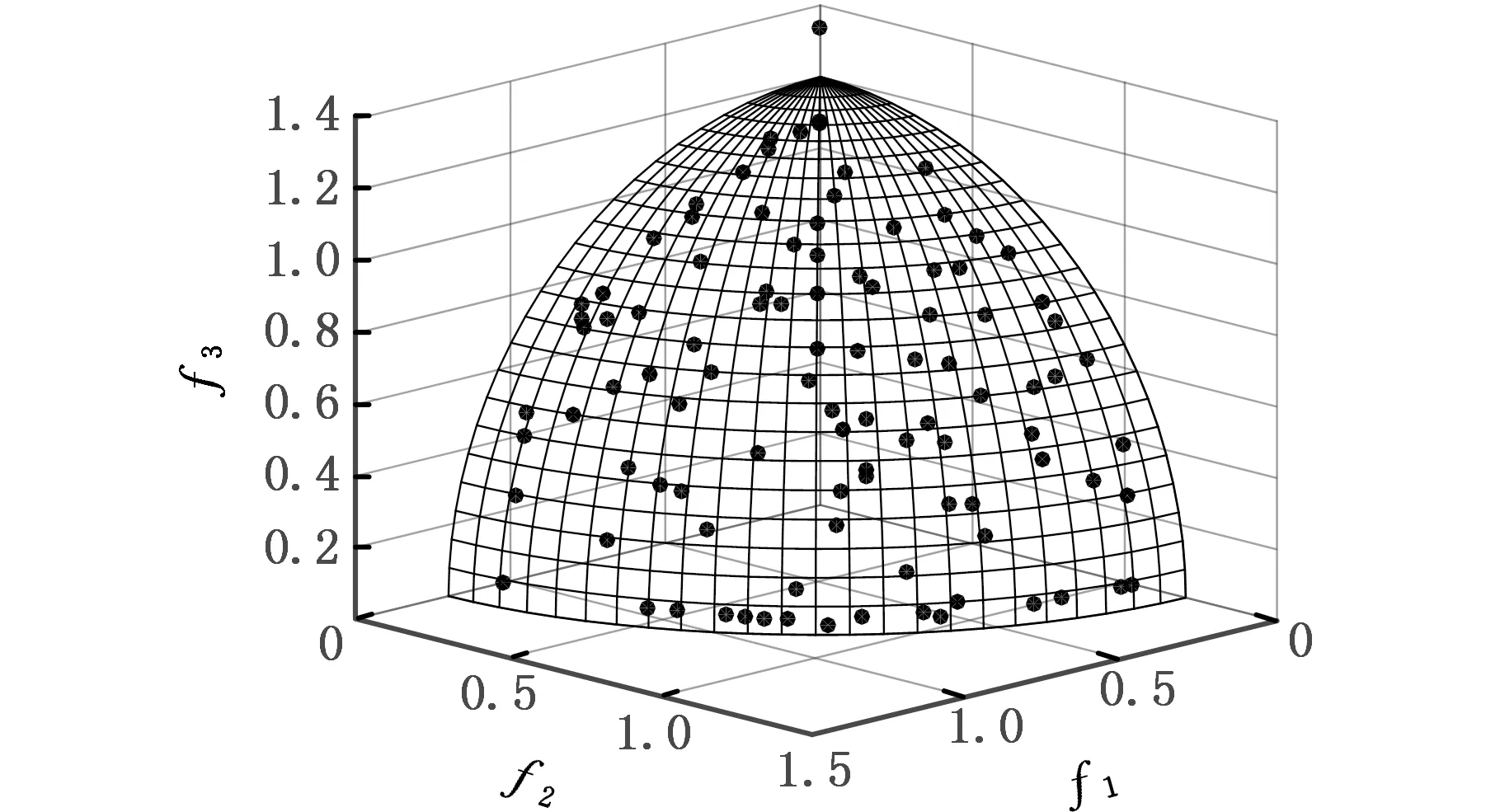
(c)CPMGAs算法Pareto解集前沿圖10 NSGAⅡ、MPSO、CPMGAs算法在DTLZ2上的Pareto前沿對比圖Fig.10 Pareto frontier contrast diagram of NSGA Ⅱ、MPSO、CPMGAs algorithm on DTLZ2

由圖9、圖10定性分析三種算法性能的對比結果可知：NSGAⅡ算法的收斂性最差，解集多樣性好，但分布不均；MPSO算法的收斂性較好且解集的分布均勻性能好；本文提出的CPMGAs的收斂性比NSGAⅡ算法好，與MPSO算法具有相同的收斂性，但解集的均勻分布性與覆蓋廣度較MPSO算法要好。

表2記錄了三種算法在測試函數ZDT3和DTLZ2上的三種性能指標。由指標性能的含義可知，在求解ZDT3和DTLZ2函數時，CPMGAs算法在收斂性(GD)和分布均勻性(TD)上比其他兩種算法更優，雖然在求解ZDT3函數上，MPSO算法也表現了較好的收斂性(GD)，但CPMGAs的標準差更小，說明在收斂性上表現更加穩定。在分布均勻性(TD)上，MPSO算法在ZDT3函數上表現最佳，而CPMGAs算法在DTLZ2函數上表現最佳，說明二者在解集分布均勻性上均有良好性能但不夠穩定。CPMGAs算法在覆蓋范圍(HV)上表現出最佳性能，是因為在模糊聚類操作中，各元胞種群間存在最大差異性，且多元胞差分進化重插入與移民操作保證了種群的多樣性與分布均勻性。因此本文的CPMGAs算法總體上能夠滿足求解多目標、多維度非線性問題，且具有良好的性能。

4.3 算例驗證

為進一步驗證算法的有效性，本文選用國際上公布的旅行商問題(traveling salesman problem,TSP)標準測試庫(TSPLIB)中的8組算例(oliver30，eil51，rand100，rand300，kroab100，kroac100，krobc100，kroab200)進行算例驗證，并與文獻[25]提出的混合遺傳算法(hybrid genetic algorithm,HGA)進行結果的對比與驗證。

參考文獻[25]，算例中的目標1為最小化總距離，目標2為最小化總成本。針對算例oliver30、eil51、rand100、rand300，與目標1相關任意兩點坐標值由標準庫所給，與目標2相關的任意兩點成本值隨機生成[25]。采用超體積(HV)、計算時間(t)、相對誤差(e)三個指標驗證本文算法解的質量。指標e的定義如下：

其中，f1為只考慮單目標TSP問題時目標1的最優值(由TSPLIB給出)，f2為考慮雙目標TSP問題時目標1的最優值，由算法計算所得。測試過程中，HGA算法的參數設置與文獻[25]一致，本文算法參數與4.1.2節一致。種群規模取50，針對算例oliver30、eil50,迭代次數取200，其余算例取500。每個算例各單獨測試10次，取指標均值，測試結果如表3所示。

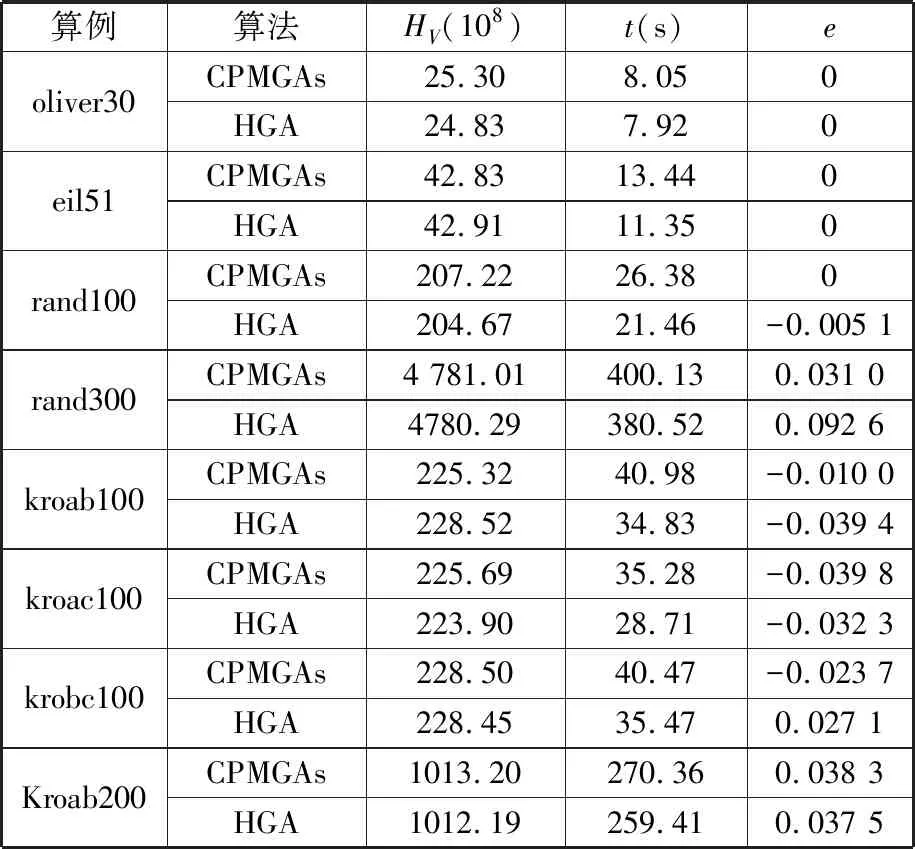
表3 算例驗證結果對比表Tab.3 Examples comparison of verification results

由表3可知，本文算法CPMGAs在超體積(HV)指標上的值比文獻[25]的HGA更高，說明解的空間范圍更廣，驗證了本文算法在計算結果的多樣性與收斂性方面更好；在計算時間上，因為存在聚類、移民等多步操作，CPMGAs所耗費的計算時間更長。在相對誤差e上，CPMGAs的值普遍更小，進一步論證了本文算法在多樣性與收斂性上具有一定的優勢。因此CPMGAs算法以相對較長的計算時長為代價，換來計算多樣性與收斂性上的相對優勢，能較好地滿足離散組合優化問題的需求。

5 企業應用分析

將多目標布局模型應用于企業布局中，研究模型的實用性。 A公司目前的生產裝配車間仍是以大規模重復的生產作業方式來滿足客戶的訂單需求。車間的總面積為100×100 m2，包括15個功能單元區域。車間物流量關系如表4所示，車間功能單元約束如表5所示，其中，S1、S2、…、S5表示5類產品編號。Y表示Yes，N表示No。車間布局現狀如圖11所示，其中，F1、F2、…、F5表示單元內的設備編號。

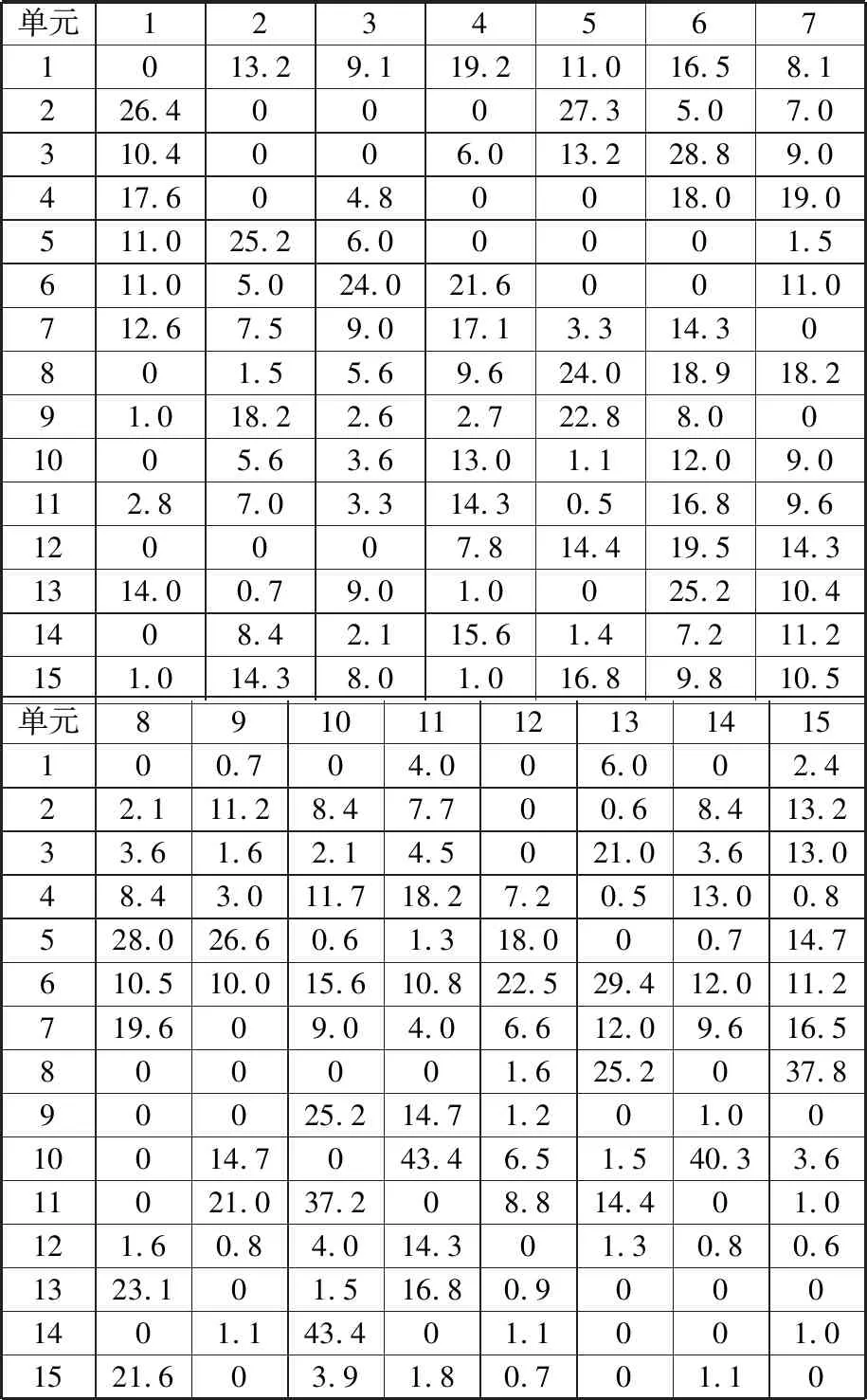
表4 車間單元間物流量關系Tab.4 Relationship of material flow among units in workshop (104元·件/m)

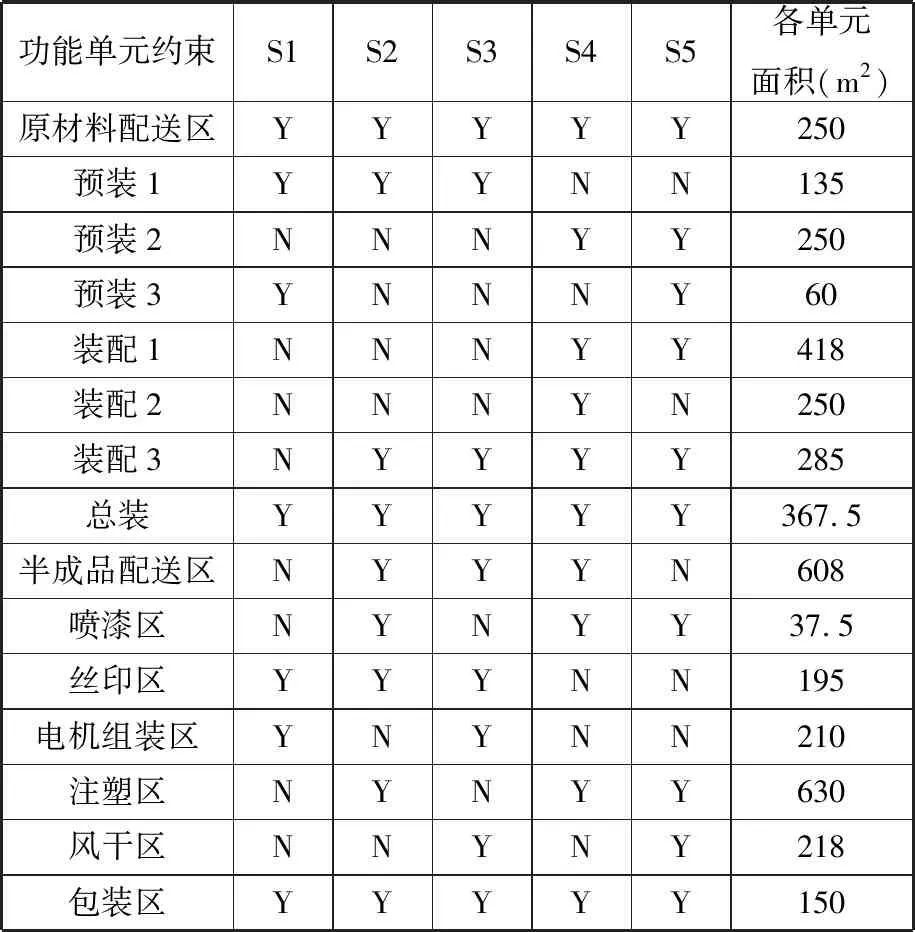
表5 產品功能單元約束Tab.6 The constraint of functional unit

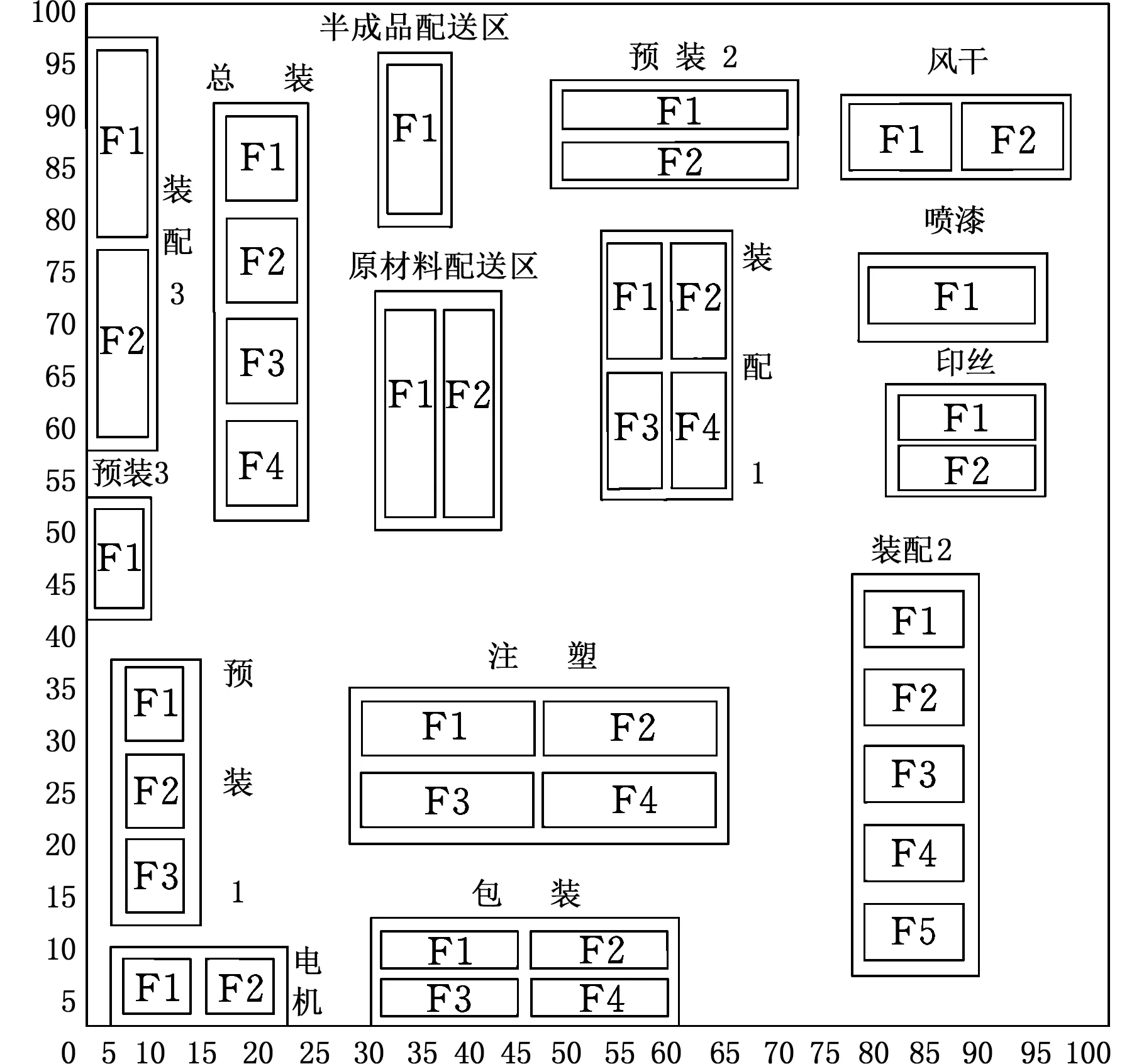
圖11 車間布局現狀圖Fig.11 Workshop layout map

利用本文模型與算法進行布局優化，參數選取：種群規模M=1 000，聚類數p=3，交叉概率Pc=0.75，變異概率Pm=0.001，移民率Y=5%，課題組在企業實地調研后，取ηopt=4/3，ηmax=5，迭代次數niter=100，用MATLAB2010a仿真計算。由于布局問題的復雜性，以算法產生的Pareto解作為最優解集，如圖12所示。

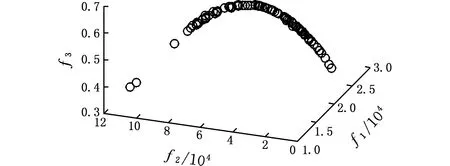
圖12 布局多目標Pareto解集前沿Fig.12 Layout multi-objective pareto solution frontier

因進化過程中的低熵化引導，所產生的布局方案的布局熵均在[0.2,0.8]的合理區間范圍內，說明布局方案均有較高的穩定性。圖13表示子目標f1與f2的解集前沿，可以看出，左上方的解具有較低的單元布置成本與較高的物流成本；右下角的解具有較高的單元布置成本與較低的物流成本。目標空間的解集能為決策者根據自己偏好提供有效布局解。解碼，得到部分布局解。

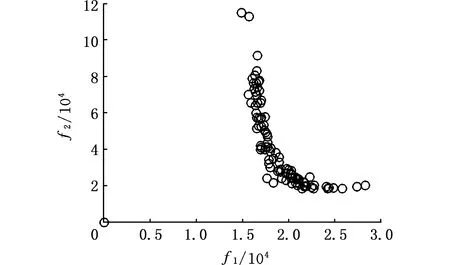
圖13 布局子目標f1與f2的Pareto解集前沿Fig.13 The Pareto solution frontier of layout subtargets f1 and f2

表6提供了部分Pareto解，選擇序號1為實例布局解進行解碼，考慮車間運輸工具等原因，規定車間長度方向、寬度方向最小間距分別是4.5 m和2.5 m，邊界間距均為5 m，解碼得到實際布局如圖14所示。

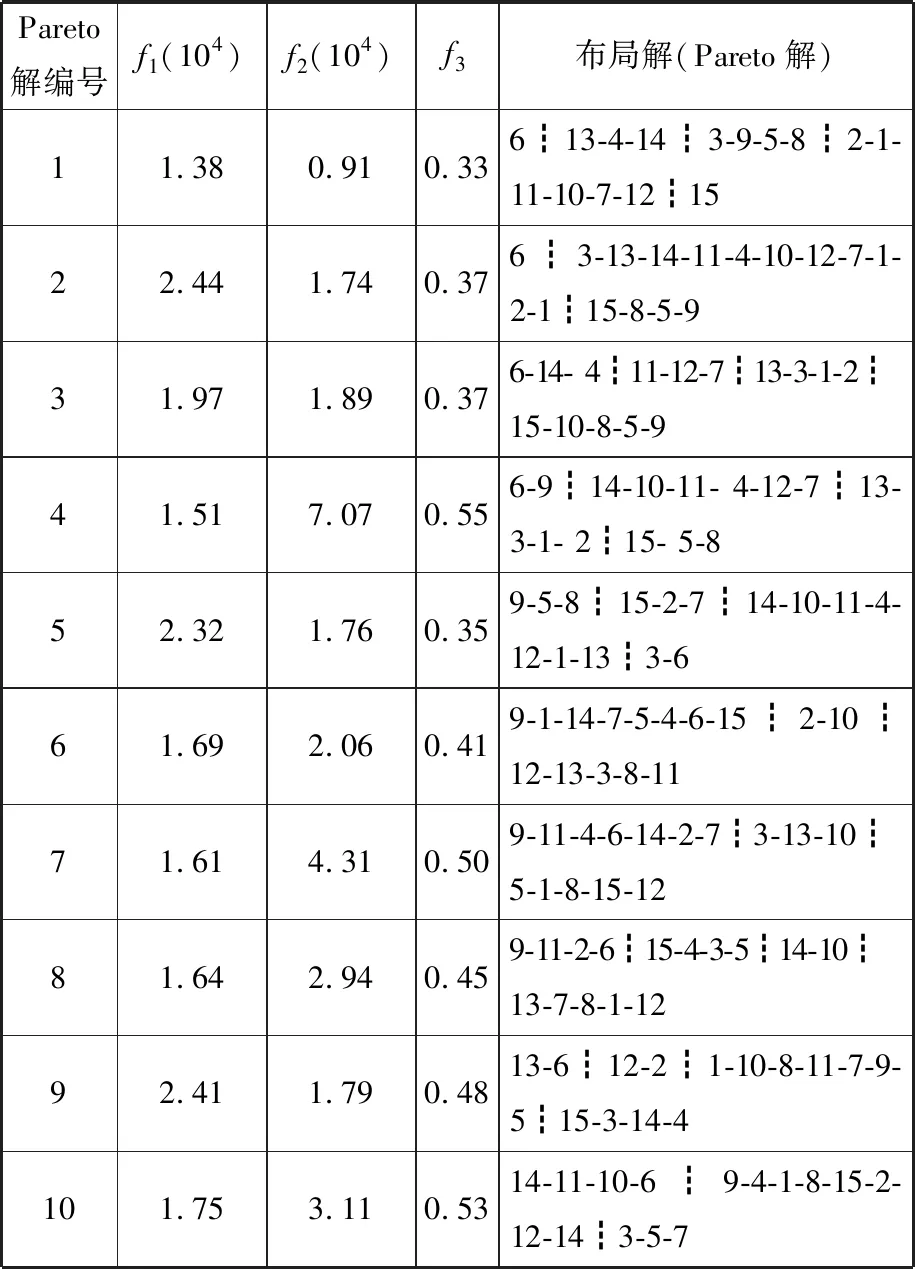
表6 Pareto解集Tab.6 Pareto solution sets

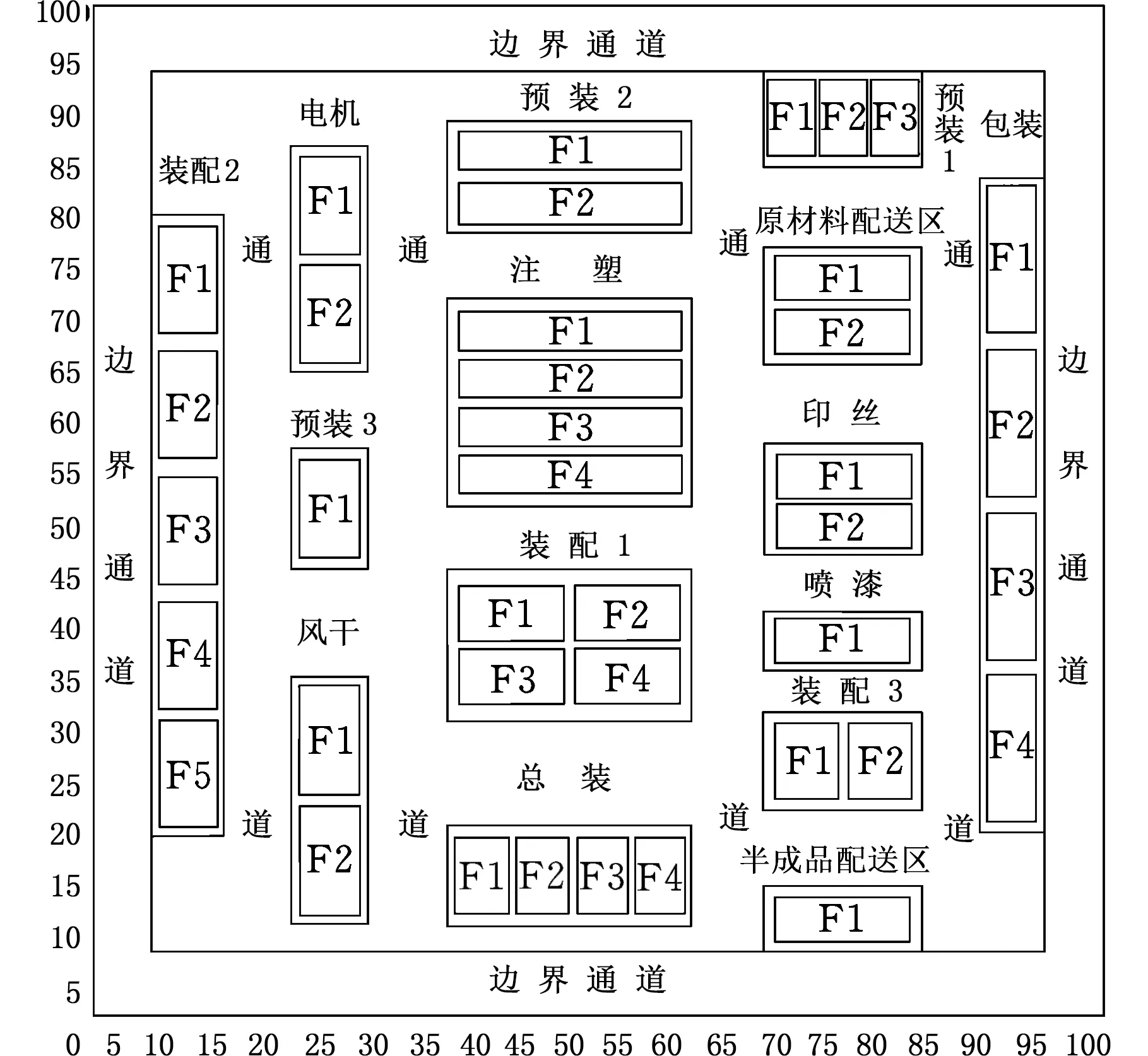
圖14 優化后的車間實際布局Fig.14 Optimized workshop layout

6 結語

隨著制造業的發展，企業不僅需要面對復雜多樣的需求波動，也需要低成本、高穩健發展以滿足可持續性。提出單位面積布置成本、單位產品物流成本與布局熵為目標的車間布局優化模型，設計聚類并行多目標遺傳算法，進行算例論證和實例驗證，有效降低了布置成本、物流成本，提高了布局穩定性，表明算法和模型的有效性和可靠性。但本文的布局過程中并沒有與產品的動態調度相結合，同時也假設了單元的規則性，在一定程度上限制了應用，在今后研究中，可以注重這一方面的研究。